Уравнения Максвелла

Лекция

Уравнения Максвелла

План лекции

1. Опыты Эрстеда (1820 г.) и Фарадея (1831 г.), взаимосвязь между электрическими и магнитными полями.
2. Фарадеевская и Максвелловская трактовки явления электромагнитной индукции.
3. Основные законы электрического и магнитного полей.
4. Обобщенный закон электромагнитной индукции Фарадея.
5. Ток смещения
6. Закон полного тока.
7. Система уравнений Максвелла в интегральной форме.
8. Уравнения Максвелла в дифференциальной форме
9. Выводы. Значения теории Максвелла.

Уравнения Максвелла. Электромагнитные волны.

Это фундаментальные уравнения классической электродинамики, описывающие электромагнитные явления в любой среде (и в вакууме). Сформулированы Максвеллом в 1860 – 1865 годах на основе обобщения эмпирических законов электрических и магнитных явлений и развитие идей английского ученого Фарадея о том, что взаимодействие между электрически заряженными телами осуществляется вследствие электромагнитного поля. Современная форма уравнений Максвелла дана немецким физиком г. Герцем и английским физиком О. Хэвисайдом.

Этот шаг был подготовлен многими исследователями, в первую очередь: М. Фарадей, Ш. Кулон, А. Ампер, Г. Эрстед, Ж. Био, Ф Саварр, П. Лаплас.

Опыты Эрстеда и Фарадея создали основу, на которой построены законы Максвелла.

Опыты

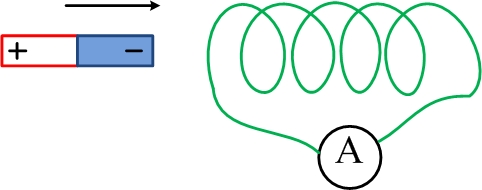
Опыт Эрстеда (1820 год)

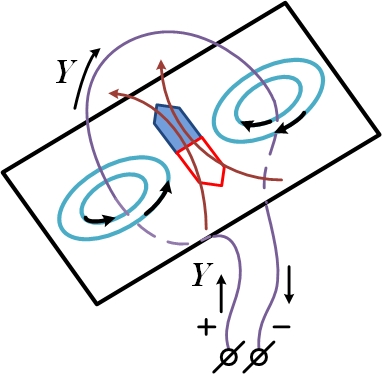
Для опыта берется проволока и вольтовая батарея. Подсоединим батарею. Магнитная игла выходит из своего первоначального положения. На магнит действует сила, перпендикулярная к плоскости кольца. Опыт показывает связь между магнетизмом и электрическим током. Сила взаимодействия между магнитом и проволокой не лежит вдоль линии, связывающей магнит и проволоку. Сила перпендикулярна этой линии.

В момент возникновения тока появляется сила. Всякий ток связан с магнитным полем. (движениями зарядов). Изменяющееся электрическое поле сопровождается магнитным полем.

Силовые линии магнитного поля замыкаются вокруг изменяющегося электрического поля (ток – это переменное электрическое поле).

Обнаружим, что провод, замыкающий клеммы вольтовой батареи, влияет на расположенный поблизости магнит.

Эрстед обнаружил, что и электрическое возмущение (ток) действует вращательным образом – магнит, помещенный вблизи провода с током, стремиться установиться перпендикулярно проводу, а при обносе вокруг провода, он всегда указывает вперед одним и тем же концом.

(обносить провод магнитом – стрелкой)

Связь между электрическим током и линиями магнитной индукции – по правому винту:

Опыт Фарадея (1831 год)

Для опыта берется соленоид, магнитный стержень, прибор для обнаружения тока.

Соленоид – замкнутая цепь.

Магнитный стержень около соленоида – тока нет. Приближаем или удаляем стержень – появляется ток. Переменное магнитное поле – создает электронами ток, электрическое поле.

Изменяющееся магнитное поле сопровождается электрическим током.

Силовые линии электрического поля замкнуты вокруг магнитного поля. Используется правило левого винта.

Опыты Эрстеда и Фарадея создали основу, на которой построены законы Максвелла, установив, таким образом, теснейшую взаимосвязь между электрическим и магнитным полем.

Изменение одного поля можно связать с изменением другого поля в точке пространства в любой момент времени.

Максвелл идет следующим путем:

Из опыта Фарадея:

Представим себе, что виток соленоида все меньше и меньше – сходится в точку – и мы получаем закон, связывающий изменение магнитного поля и изменение электрического поля в любой момент времени в любой точке пространства. – Это один из принципиальных шагов к уравнениям Максвелла.

Так же можно рассмотреть и другую основу теории поля, опирающуюся на опыт Эрстеда:

Стягивая витки магнитных силовых линий к точке, мы получаем – изменяющееся электрическое поле порождает изменяющееся магнитное поле в точке в любой момент времени.

Это как бы два полушага, дающие один шаг – он дает связь между изменениями магнитных и электрических полей в любой точке пространства в любой момент времени.

Но понадобился еще один шаг, сделанный Максвеллом.

Согласно опыту Фарадея необходим проводник для обнаружения электрического поля, а в опыте Эрстеда необходимо магнитный полюс – игла для обнаружения магнитного поля.

Теория идей Максвелла идет дальше этих экспериментальных фактов.

Электрическое и магнитное поля согласно воззрениям Максвелла должны быть чем – то реальным. Электрическое поле создается изменяющимся магнитным полем совершенно независимо от того, есть ли проводник или нет. Магнитное поле создается изменяющимся электрическим полем независимо от того есть ли магнитная стрелка или нет.

Таким образом, к уравнениям Максвелла приводят два шага:

Первый шаг: В опыте Эрстеда круговые линии магнитного поля, замыкающиеся вокруг тока и изменяющегося электрического поля, должны быть стянуты к точке.

В опыте Фарадея круговые линии электрического поля, замыкающиеся вокруг изменяющегося магнитного поля, должны быть стянуты к точке.

Второй шаг: Трактовка поля как реального объекта.

В основу теории поля. (В точке – дифференциальная форма).

Уравнения Максвелла описали структуру электромагнитного поля. Арена этих законов – все пространство (о едином электромагнитном поле).

I. Первым шагом на пути построения теории поля была идея Максвелла о возможности построения закона, связывающего изменение магнитного поля с изменением электрического поля.

II. Второй шаг.

Электрическое и магнитное поле – реальные объекты.

Электрическое поле создается изменяющимся магнитным полем совершенно независимо от того, есть проводник или нет.

Магнитное поле создается изменяющимся электрическим полем независимо от того, есть стрелка или ее нет.

Он опирался на основные законы электрического и магнитного поля.

Уравнения Максвелла в интегральной форме.

Основные законы электрического и магнитного полей следующие:

1) Теорема Гаусса для электрического поля:

2) Так как свободных магнитных зарядов нет, то теорема Гаусса для магнитного поля:

3) Критерием потенциальности поля являются величина циркуляции его вектора напряженности =0

В электростатике:

Электростатическое поле потенциально.

В случае существования полей сторонних сил – полей неэлектростатического происхождения:

Поля сторонних сил непотенциальны – они вихревые.

Закон электромагнитной индукции Фарадея:

где

Отсюда:

Интеграл в правой части берется по произвольной поверхности, опирающейся на контур. Поскольку поверхность и контур неподвижны, операции дифференцирования по времени и интегрирования по поверхности можно поменять местами:

провод в контуре

Вектор зависит как от времени, так и от координат, поэтому - дифференциал по времени – частная производная.

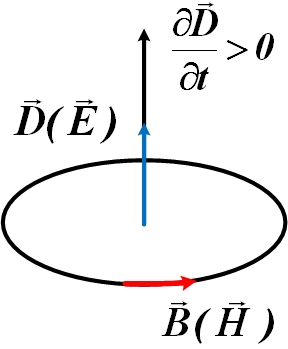
Таким образом, переменное магнитное поле создает вихревое электрическое поле ( (вихрь)), связанное с правилом левого винта.

Как создать вихревое магнитное поле ?

Если переменное магнитное поле создает вихревое электрическое, то движение электрических зарядов - переменное электрическое поле. Ток создает вихревое магнитное поле :

где

(ток проводимости)

Между величинами ; ; ; ; входящими в вышеперечисленные уравнения существуют известные соотношения:

( - электропроводность)

Это основные законы электрического и магнитного полей и легли в основу теории Максвелла.

Основное содержание теоремы Максвелла можно сформулировать в виде двух гипотез:

Первая гипотеза Максвелла – обобщенный закон электромагнитной индукции Фарадея:

Любое изменяющееся во времени магнитное поле вызывает появление вихревого электрического поля:

(I)

Везде, всюду (в вакууме). У Фарадея – только в проводнике

Или:

Циркуляция напряженности электрического поля по произвольному контуру равна со знаком (-) производной по времени потока магнитной индукции через любую поверхность, опирающуюся на контур:

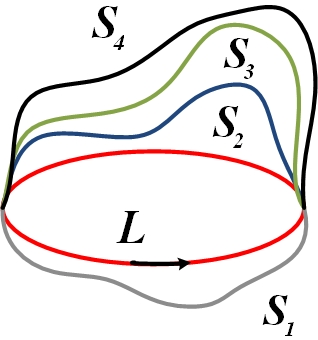
Здесь устанавливается количественная связь между изменяющимся магнитным полем и вихревым электрическим .

Согласно Фарадею ЭДС индукции возникает в проводящем контуре.

Максвелл предположил, что изменяющееся со временем магнитное поле обуславливает появление в пространстве вихревого электрического поля , независимо от присутствия проводящего контура. Это первое уравнение Максвелла.

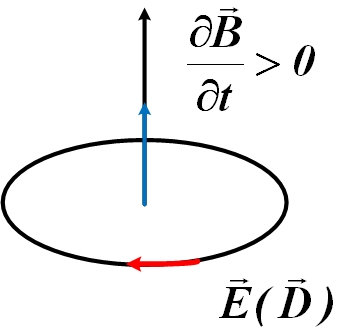
В результате анализа различных электромагнитных процессов Максвелл пришел к выводу, что должно существовать и обратное явление: всякое изменение во времени электрического поля вызывает появление вихревого магнитного поля. Это вторая гипотеза Максвелла.

Так как магнитное поле есть обязательный признак всякого тока, то Максвелл назвал переменное электрическое поле током смещения, в отличие от тока проводимости, обусловленного движением заряженных частиц, совершенно не связанного с движением зарядов.

Открытие Максвеллом тока смещения – наиболее существенный и решающий шаг, сделанный Максвеллом при построении теории электромагнитного поля. Это открытие аналогично открытию электромагнитной индукции: переменное магнитное поле возбуждает вихревое электрическое поле.

Это было чисто теоретическое открытие – потом было подтверждено экспериментами.

Рассмотрим цепь переменного тока, содержащую конденсатор. Ток проводимости везде, кроме зазора конденсатора:

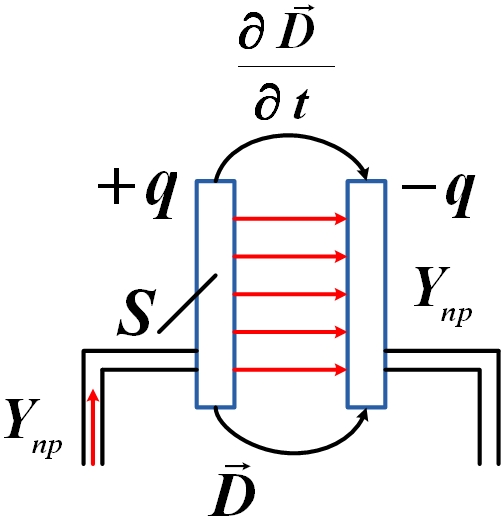
Линии тока проводимости терпят разрыв, зато в пространстве между обкладками есть переменное электрическое поле (). Максвелл предположил, что линии тока проводимости непрерывно переходят на границе обкладок конденсатора в линии тока смещения, то есть ток проводимости в металлическом проводнике замыкается током смещения в диэлектрике.

В таком случае плотности равны:

но

поверхностная плотность заряда

Но известно (для изотропной среды):

Следовательно:

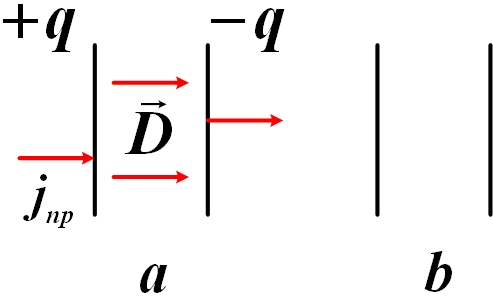
Наиболее общим свойством каждого тока является способность создавать магнитное поле. Магнитное поле токов проводника было открыто Эрстедом в 1820 году. Величина его определяется законом Био – Саварра – Лапласа (1820 год).

В 1901 году А.А. Эйхенвальд показал, что конвекционные токи, образованные движением в пространстве заряженных тел и поляризованных диэлектриков, создают такое же магнитное поле, как и токи проводимости

В 1911 году Иоффе А.Ф. обнаружил магнитное поле электронов, движущихся в вакууме, так же эквивалентное току проводимости.

Из всех физических свойств, присущих току Максвелл приписал току смещения лишь одно – способность создавать магнитное поле, аналогично магнитному полю токов проводника:

Если в проводнике переменный ток, то внутри проводника есть и ток проводимости, и ток смещения, и магнитное поле определяется полным током:

Тогда:

II.

Закон полного тока.

Ток смещения есть там, где меняется со временем электрическое поле. В диэлектриках ток смещения состоит из двух различных слагаемых:

- ток смещения (плотность тока); - плотность тока поляризации, обусловленная движением связанных зарядов.

Ток поляризации возбуждает магнитное поле – эти токи не отличаются по природе о токов проводимости.

Принципиально новое – - не связано ни с каким движением зарядов, а только с изменением электрического поля - - возбуждает магнитное поле.

Даже в вакууме всякое изменение электрического поля возбуждает в окружающем пространстве магнитное поле.

- открытие тока смещения – к открытию электромагнитного поля.

Ваша специальность включает исследование свойств материалов в электрических и магнитных полях.

Сравним величины токов проводимости и токов смещения для различных материалов:

Пусть синусоидальное поле:

(отношение амплитуд):

В вакууме:

Таким образом, при обычных частотах в металлах токи смещения малы по сравнению с токами проводимости. Они соизмеримы при Гц – это несколько ангстрем – рентгеновские лучи.

В полупроводниках токи проводимости и токи смещения одного порядка при Гц (дециметровый диапазон).

В диэлектриках токи смещения больше токов проводимости уже при низких частотах (переменный ток).

Дополнив основные факты из области электромагнетизма установлением магнитных действий токов смещения, Максвелл смог написать систему фундаментальных уравнений электродинамики:

Материальные уравнения:

8. Уравнение Максвелла в дифференциальной форме

Уравнения Максвелла применимы к поверхности любой величины и поэтому входящие в них величины относятся к разным точкам поля. Так, например, в уравнении:

- напряженность магнитного поля в точках контура , Ограничивающего поверхность S, в то время как поток вектора зависит от значения в точках самой поверхности.

Можно, однако, преобразовать эти уравнения в такую форму, чтобы все величины относились к одной и той же точке поля. Для этого уравнения Максвелла нужно применить к поверхности бесконечно малой величины.

Согласно теореме Стокса:

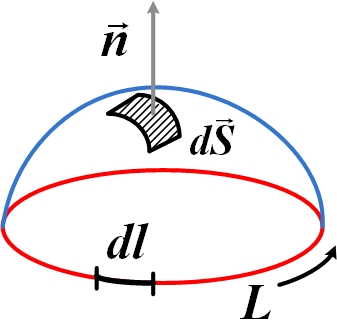
Тогда первое уравнение:

(I)

Справа интеграл зависит только от времени, при фиксированном контуре правая часть никак не меняется при любых изменениях .

Символ ;

Второе уравнение:

По теореме Стокса:

(II)

Расхождения электрической и магнитной индукции

Третье и четвертое уравнения Максвелла:

Переход от интегральной к дифференциальной форме согласно теореме Остроградского – Гаусса:

(3)

(4)

Схема уравнений Максвелла в дифференциальной форме:

( - удельная проводимость)

Выводы. Значения теории Максвелла.

1.Уравнения Максвелла не выводятся.

2.Уравнения Максвелла позволяют определить основные характеристики поля (, , , ) в каждой точке пространства в любой момент времени, если известны источники поля, плотность тока и плотность заряда .

3.Сама по себе система уравнений Максвелла не имеет определенных решений, то есть совокупность ; ; ; ; ; как конкретных функций координат и времени, существует только при наложении дополнительных условий, характеризующих тот или иной реальный объект.

Уравнения Максвелла