Дифференциальное исчисление функции нескольких переменных

лухов Ю.П. Конспект лекций по высшей математике. 6

Лекция 22

ТЕМА: Дифференциальное исчисление функции нескольких переменных

План.

1. Дифференцирование сложных функций. Инвариантность формы дифференциала.
2. Неявные функции, условия их существования. Дифференцирование неявных функций.
3. Частные производные и дифференциалы высших порядков, их свойства.*
4. Касательная плоскость и нормаль к поверхности. Геометрический смысл дифференциала. Формула Тейлора для функции нескольких переменных.*
5. Производная функции по направлению. Градиент и его свойства.

Дифференцирование сложных функций

Пусть аргументы функции z = f (x, y) являются, в свою очередь, функциями переменных u и v: x = x (u, v), y = y (u, v). Тогда функция f тоже есть функция от u и v. Выясним, как найти ее частные производные по аргументам u и v, не делая непосредственной подстановки z = f ( x(u, v), y(u, v)). При этом будем предполагать, что все рассматриваемые функции имеют частные производные по всем своим аргументам.

Зададим аргументу u приращение u, не изменяя аргумент v. Тогда

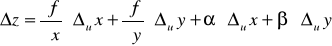. (16.1)

Если же задать приращение только аргументу v, получим:

. (16.2)

Разделим обе части равенства (16.1) на u, а равенства (16.2) – на v и перейдем к пределу соответственно при u0 и v0. Учтем при этом, что в силу непрерывности функций х и у . Следовательно,

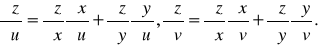(16.3)

Рассмотрим некоторые частные случаи.

Пусть x = x(t), y = y(t). Тогда функция f (x,y) является фактически функцией одной переменной t , и можно, используя формулы (43) и заменяя в них частные производные х и у по u и v на обычные производные по t (разумеется, при условии дифференцируемости функций x(t) и y(t) ) , получить выражение для :

(16.4)

Предположим теперь, что в качестве t выступает переменная х, то есть х и у связаны соотношением у = у (х). При этом, как и в предыдущем случае, функция f является функцией одной переменной х. Используя формулу (16.4) при t = x и учитывая, что , получим, что

. (16.5)

Обратим внимание на то, что в этой формуле присутствуют две производные функции f по аргументу х: слева стоит так называемая полная производная, в отличие от частной, стоящей справа.

Примеры.

1. Пусть z = xy, где x = u + v, y = uv. Найдем и . Для этого предварительно вычислим частные производные трех заданных функций по каждому из своих аргументов:

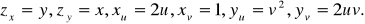Тогда из формулы (16.3) получим: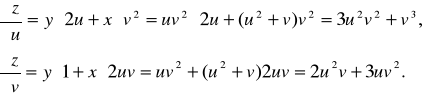

(В окончательный результат подставляем выражения для х и у как функций u и v).

1. Найдем полную производную функции z = sin (x + y), где y = cos x.

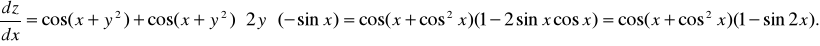
Инвариантность формы дифференциала

Воспользовавшись формулами (15.8) и (16.3), выразим полный дифференциал функции

z = f (x, y) , где x = x(u,v), y = y(u,v), через дифференциалы переменных u и v:

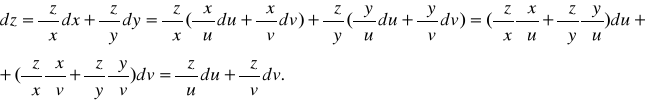(16.6)

Следовательно, форма записи дифференциала сохраняется для аргументов u и v такой же, как и для функций этих аргументов х и у, то есть является инвариантной (неизменной).

Неявные функции, условия их существования

Определение. Функция у от х, определяемая уравнением

F (x, y) = 0 , (16.7)

называется неявной функцией.

Конечно, далеко не каждое уравнение вида (16.7) определяет у как однозначную (и, тем более, непрерывную) функцию от х. Например, уравнение эллипса

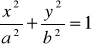
задает у как двузначную функцию от х: 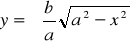для

Условия существования однозначной и непрерывной неявной функции определяются следующей теоремой:

Теорема 1 (без доказательства). Пусть:

1. функция F (x,y) определена и непрерывна в некотором прямоугольнике с центром в точке (х0 , у0 );
2. F (x0 , y0 ) = 0 ;
3. при постоянном х F (x,y) монотонно возрастает (или убывает) с возрастанием у.

Тогда

а) в некоторой окрестности точки (х0 , у0 ) уравнение (16.7) определяет у как однозначную функцию от х: y = f(x);

б) при х = х0 эта функция принимает значение у0 : f (x0) = y0 ;

в) функция f (x) непрерывна.

Найдем при выполнении указанных условий производную функции y = f (x) по х.

Теорема 2. Пусть функция у от х задается неявно уравнением (16.7), где функция F (x,y) удовлетворяет условиям теоремы 1. Пусть, кроме того, 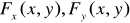- непрерывные функции в некоторой области D, содержащей точку (х,у), координаты которой удовлетворяют уравнению (16.7), причем в этой точке 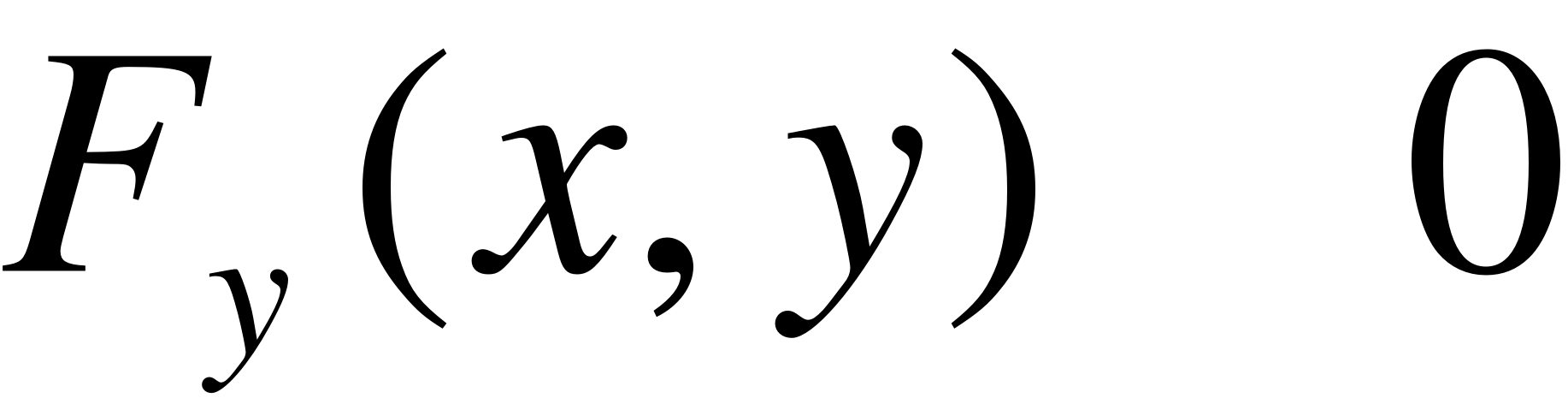. Тогда функция у от х имеет производную

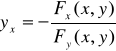(16.8)

Доказательство.

Выберем некоторое значение х и соответствующее ему значение у. Зададим х приращение х, тогда функция y = f (x) получит приращение у . При этом F (x,y) = 0, F (x+ x, y+y) = 0, поэтому F (x+ x, y+y) – F (x,y) = 0. Слева в этом равенстве стоит полное приращение функции F (x,y), которое можно представить в виде (15.5):

.

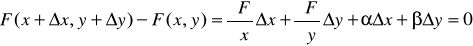Разделив обе части полученного равенства на х, выразим из него : .

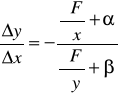В пределе при 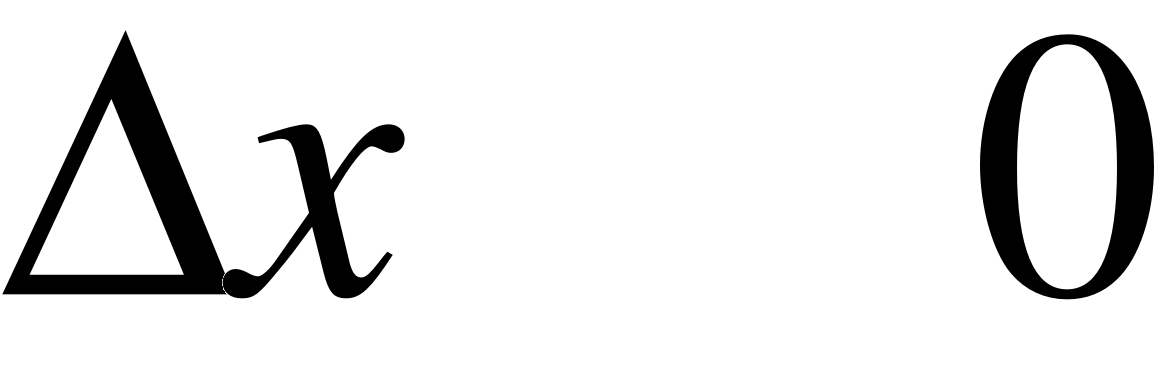, учитывая, что 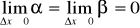и 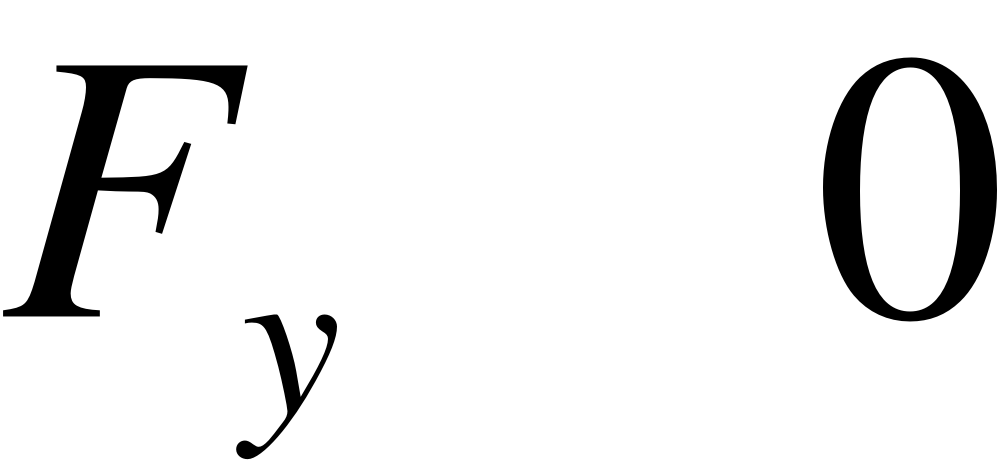, получим: 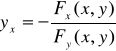. Теорема доказана.

Пример. Найдем , если . Найдем , .

Тогда из формулы (16.8) получаем: .

Производные и дифференциалы высших порядков

Частные производные функции z = f (x,y) являются, в свою очередь, функциями переменных х и у. Следовательно, можно найти их частные производные по этим переменным. Обозначим их так:

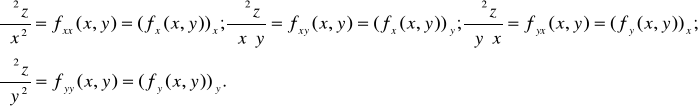
Таким образом, получены четыре частные производные 2-го порядка. Каждую из них можно вновь продифференцировать по х и по у и получить восемь частных производных 3-го порядка и т.д. Определим производные высших порядков так:

Определение. Частной производной n-го порядка функции нескольких переменных называется первая производная от производной (n – 1)-го порядка.

Частные производные обладают важным свойством: результат дифференцирования не зависит от порядка дифференцирования (например, ).

Докажем это утверждение.

Теорема 3. Если функция z = f (x,y) и ее частные производные 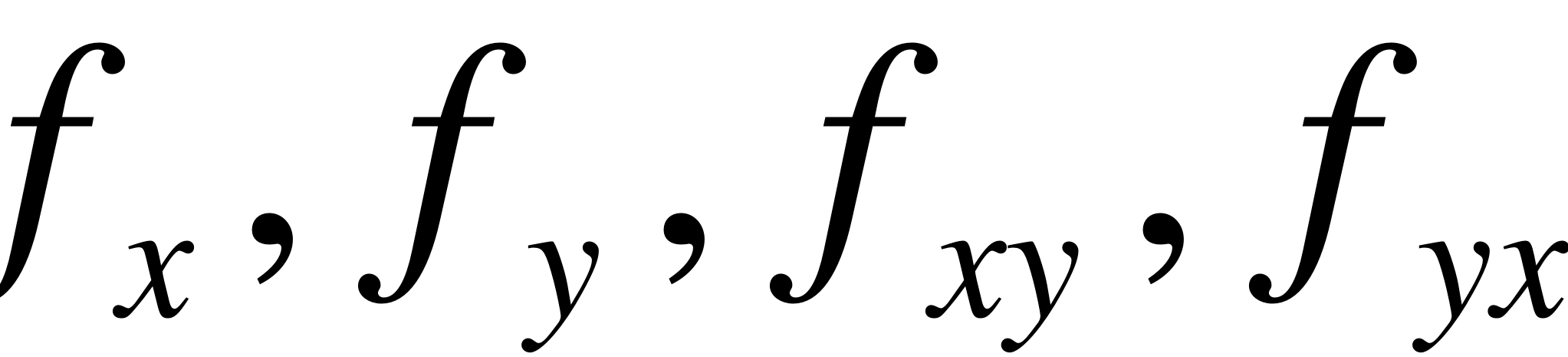определены и непрерывны в точке М (х, у) и в некоторой ее окрестности, то в этой точке

(16.9)

Доказательство.

Рассмотрим выражение и введем вспомогательную функцию . Тогда

. Из условия теоремы следует, что дифференцируема на отрезке [x, x+x], поэтому к ней можно применить теорему Лагранжа: где

[x, x+x]. Но Так как в окрестности точки М определена , дифференцируема на отрезке [y, y + y], поэтому к полученной разности вновь можно применить теорему Лагранжа: , где Тогда

Изменим порядок слагаемых в выражении для А:

и введем другую вспомогательную функцию , тогда Проведя те же преобразования, что и для , получим, что где . Следовательно,

. В силу непрерывности и . Поэтому, переходя к пределу при получаем, что , что и требовалось доказать.

Следствие. Указанное свойство справедливо для производных любого порядка и для функций от любого числа переменных.

Дифференциалы высших порядков

Определение. Дифференциалом второго порядка функции u = f (x, y, z) называется

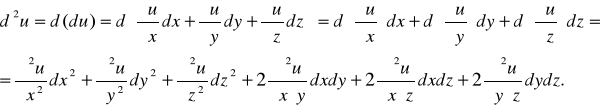
Аналогично можно определить дифференциалы 3-го и более высоких порядков:

Определение. Дифференциалом порядка k называется полный дифференциал от дифференциала порядка (k – 1): d k u = d (d k-1 u).

Свойства дифференциалов высших порядков

1. k-й дифференциал является однородным целым многочленом степени k относительно дифференциалов независимых переменных, коэффициентами при которых служат частные производные k-го порядка, умноженные на целочисленные постоянные (такие же, как при обычном возведении в степень):

.

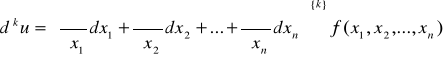1. Дифференциалы порядка выше первого не инвариантны относительно выбора переменных.

Касательная плоскость и нормаль к поверхности. Геометрический смысл дифференциала

Пусть функция z = f (x, y) является дифференцируемой в окрестности точки М (х0 , у0). Тогда ее частные производные и являются угловыми коэффициентами касательных к линиям пересечения поверхности z = f (x, y) с плоскостями у = у0 и х = х0, которые будут касательными и к самой поверхности z = f (x, y). Составим уравнение плоскости, проходящей через эти прямые. Направляющие векторы касательных имеют вид {1; 0; } и {0; 1; }, поэтому нормаль к плоскости можно представить в виде их векторного произведения: n = {-,-, 1}. Следовательно, уравнение плоскости можно записать так:

, (16.10)

где z0 = .

Определение. Плоскость, определяемая уравнением (16.10), называется касательной плоскостью к графику функции z = f (x, y) в точке с координатами ( х0 , у0 , z0 ).

Из формулы (15.6) для случая двух переменных следует, что приращение функции f в окрестности точки М можно представить в виде:

или

(16.11)

Следовательно, разность между аппликатами графика функции и касательной плоскости является бесконечно малой более высокого порядка, чем , при 0.

При этом дифференциал функции f имеет вид:

,

что соответствует приращению аппликаты касательной плоскости к графику функции. В этом состоит геометрический смысл дифференциала.

Определение. Ненулевой вектор, перпендикулярный касательной плоскости в точке М (х0 , у0) поверхности z = f (x, y), называется нормалью к поверхности в этой точке.

В качестве нормали к рассматриваемой поверхности удобно принять вектор --n = {,,-1}.

z

z = f (x,y)

M0 (x0 , y0 , z0)

n

y

M (x0 , y0)

x

Пример.

Составим уравнение касательной плоскости к поверхности z = xy в точке М (1; 1). При х0 = у0 = 1 z0 =1; . Следовательно, касательная плоскость задается уравнением: z = 1 + (x – 1) + (y – 1), или x + y – z – 1 = 0. При этом вектор нормали в данной точке поверхности имеет вид: n = {1; 1; -1}.

Найдем приращение аппликат графика функции и касательной плоскости при переходе от точки М к точке N(1,01; 1,01).

z = 1,01 - 1 = 0,0201; zкас = (1,01 + 1,01 – 1) – (1 + 1 – 1) = 0,02. Следовательно,

dz = zкас = 0,02. При этом z – dz = 0,0001.

Формула Тейлора для функции нескольких переменных

Как известно, функцию F(t) при условии существования ее производных по порядок n+1 можно разложить по формуле Тейлора с остаточным членом в форме Лагранжа (см. формулы (21), (25)). Запишем эту формулу в дифференциальной форме:

(16.12)

где

В этой форме формулу Тейлора можно распространить на случай функции нескольких переменных.

Рассмотрим функцию двух переменных f(x, y), имеющую в окрестности точки (х0 , у0) непрерывные производные по (n + 1)-й порядок включительно. Зададим аргументам х и у некоторые приращения х и у и рассмотрим новую независимую переменную t:

(0 t 1). Эти формулы задают прямолинейный отрезок, соединяющий точки (х0 , у0) и (х0 + х, у0 + у). Тогда вместо приращения f (x0 ,y0) можно рассматривать приращение вспомогательной функции

F(t) = f (x0 + t x, y0 + ty) , (16.13)

равное F (0) = F (1) – F (0). Но F (t) является функцией одной переменной t, следовательно, к ней применима формула (16.12). Получаем:

.

Отметим, что при линейной замене переменных дифференциалы высших порядков обладают свойством инвариантности, то есть

Подставив эти выражения в (16.12), получим формулу Тейлора для функции двух переменных:

, (16.14)

где 0<<1.

Замечание. В дифференциальной форме формула Тейлора для случая нескольких переменных выглядит достаточно просто, однако в развернутом виде она весьма громоздка. Например, даже для функции двух переменных первые ее члена выглядят так:

Производная по направлению. Градиент

Пусть функция u = f (x, y, z) непрерывна в некоторой области D и имеет в этой области непрерывные частные производные. Выберем в рассматриваемой области точку M(x,y,z) и проведем из нее вектор S, направляющие косинусы которого cos, cos, cos. На векторе S на расстоянии s от его начала найдем точку М1(х+х, у+у, z+z), где

Представим полное приращение функции f в виде:

где

После деления на s получаем:

.

Поскольку предыдущее равенство можно переписать в виде:

(16.15)

Определение. Предел отношения при называется производной от функции u = f (x, y, z) по направлению вектора S и обозначается .

При этом из (16.15) получаем:

(16.16)

Замечание 1. Частные производные являются частным случаем производной по направлению. Например, при получаем:

.

Замечание 2. Выше определялся геометрический смысл частных производных функции двух переменных как угловых коэффициентов касательных к линиям пересечения поверхности, являющейся графиком функции, с плоскостями х = х0 и у = у0. Аналогичным образом можно рассматривать производную этой функции по направлению l в точке М(х0 , у0) как угловой коэффициент линии пересечения данной поверхности и плоскости, проходящей через точку М параллельно оси Oz и прямой l.

Определение. Вектор, координатами которого в каждой точке некоторой области являются частные производные функции u = f (x, y, z) в этой точке, называется градиентом функции u = f (x, y, z).

Обозначение: grad u = .

Свойства градиента

1. Производная по направлению некоторого вектора S равняется проекции вектора grad u на вектор S.

Доказательство. Единичный вектор направления S имеет вид eS ={cos, cos, cos}, поэтому правая часть формулы (16.16) представляет собой скалярное произведение векторов grad u и es, то есть указанную проекцию.

1. Производная в данной точке по направлению вектора S имеет наибольшее значение, равное |grad u |, если это направление совпадает с направлением градиента. Доказательство. Обозначим угол между векторами S и grad u через . Тогда из свойства 1 следует, что

|grad u |cos, (16.17)

следовательно, ее наибольшее значение достигается при =0 и равно |grad u |.

1. Производная по направлению вектора, перпендикулярного к вектору grad u , равна нулю.

Доказательство. В этом случае в формуле (16.17)

1. Если z = f (x,y) – функция двух переменных, то grad f = направлен перпендикулярно к линии уровня f (x,y) = c, проходящей через данную точку.

афедра информатики и высшей математики КГПУ

Дифференциальное исчисление функции нескольких переменных