Электромагнитное излучение и вещество
ТЕМА 2
Электромагнитное излучение и вещество
Уровни энергии и спектры
Уровни энергии атома или молекулы можно получить экспериментально, изучая спектры поглощения или испускания, а также теоретически, решая квантовомеханическую задачу для заданной частицы как многоэлектронной системы. В атомной спектроскопии атом рассматривается как многоэлектронная система, состоящая из неподвижного ядра и движущихся вокруг него в центрально-симметричном поле одного или нескольких электронов. В квантовой механике хорошо разработаны методы решения таких задач, которые позволяют получать значения энергии с необходимой точностью. В настоящее время оба метода, обычно в сочетании друг с другом, находят широкое применение. Рассмотрим решение задачи для простейшего атома водорода, состоящего из одного электрона и протона. Уравнение Шредингера для такой системы имеет вид:
=E,
где – оператор энергии, учитывающий кинетическую и потенциальную энергию электронов в поле ядра =Т+V; T– оператор кинетической энергии; V– оператор потенциальной энергии. Уравнение (1.1) относительно неизвестных собственных функций имеет решение при всех значениях энергии E, а только при некоторых дискретных значениях E1, E2, E3, E4. Это и есть значения энергии, которыми может обладать рассматриваемая система. Правда, на волновую функцию, зависящую от координат (х, y, z) электрона, намечаются условия однозначности, конечности и непрерывности.
Стационарное уравнение Шредингера для электрона в атоме водорода имеет вид
где h – постоянная Планка; m – масса электрона; v – потенциальная энергия; E – полная энергия электрона;
Решив это уравнение, получим дискретный ряд значений энергии
где m – масса электрона; h – постоянная Планка, равная 6,626 10–24;
e – заряд электрона; n – целое число, принимающее значения n = 1, 2, 3, …, . Этот дискретный ряд сходится к границе ионизации атома при
n = (En = 0). При переходе электрона с более высоких уровней энергии (при n = 1) на самый низкий (n = 2, 3, …) получаем линейчатый спектр, соответствующий серии Лаймана, расположенный в ультрафиолетовой области ~ 30000 см–1.
Следует отметить, что подавляющее число сведений об уровнях энергии атомов и молекул получено экспериментальным путем исследования спектров поглощения и испускания, так как теоретический путь решения задачи для многоэлектронных систем имеет ограниченную применимость. Правда, в последнее время получили широкое распространение полуэмпирические (комбинированные) методы решения многоэлектронных задач, суть которых заключается в том, что во многих случаях конкретных задач находятся приближенные значения энергии и закономерности в расположении их уровней. Постоянные, которые входят в соотношения для значений энергии, определяются из опыта.
Перейдем к классификации уровней энергии молекулярной системы. Рассмотрим сначала отдельную молекулу, состоящую из взаимодействующих между собой атомов. С точки зрения квантовой механики – это многоядерная и многоэлектронная система. Найти уровни энергии такой системы можно только приближенными методами. Наряду с движением электронов здесь необходимо учитывать и движение ядер – колебательное, вращательное и поступательное. Полная энергия молекулы будет состоять из нескольких слагаемых, каждое из которых характеризует свое движение:
E = Eэл + Eкол + Eвр + Eпост+ Eвз ,
где Eпост характеризует поступательную энергию молекулы (как целое), Eвз – энергию взаимодействия между электронной, колебательной и колебательно-вращательной формами движения. Уравнение Шредингера для такой молекулы может быть представлено в виде
(эл+кол+вр+пост+вз)=E
где эл, кол, вр, пост, вз – операторы энергии, зависящие от координат электронов и ядер, характеризующих каждый вид движения. В энергетическом плане необходимо рассматривать все уровни энергии, соответствующие указанным видам движения. Однако теоретически решить задачу с таким сложным гамильтонианом не представляется возможным. Поэтому в теории надо прибегать к ряду упрощений, чтобы хотя бы приближенно решить задачу о нахождении уровней энергии. Первым упрощением является равенство нулю оператора Нвз, тогда в уравнении Шредингера можно разделить переменные. Будем пренебрегать энергией поступательного движения молекулы как целого в силу отсутствия дискретного характера энергии в указанном виде движения. Остановимся только на трех основных видах движения в молекуле – электронном, колебательном и вращательном. Всем этим видам движения будут соответствовать свои уровни энергии и соответствующие им спектры (электронные, колебательные и вращательные), а полную энергию молекулы будем представлять в виде суммы
,
Однако движение электронов молекулы, ее колебания и вращения связаны между собой. Поэтому каждое ее стационарное состояние характеризуется как электронно-колебательно-вращательное. Энергетический спектр такой молекулы достаточно сложен и его интерпретация была бы невозможной, если бы не ряд упрощений, которые принимают в теории, если учесть особенности внутренних взаимодействий, обусловленных различием масс электронов и ядер. Это позволяет во многих задачах производить разделение электронного, колебательного и вращательного движений. Возможность разделения всех видов движения в молекуле определяется не только наличием большого числа атомов, но и величиной и спецификой внутримолекулярных взаимодействий, а также степенью перекрытия ее энергетического спектра.
В основе разделения всех видов движения в молекуле на электронное, колебательное и вращательное лежит предположение о медленности движения ядер по сравнению с движением электронов и медленности вращений молекулы как целого по сравнению с колебаниями ядер. Прежде всего это проявляется в значениях частот электронных переходов, которые составляют несколько тысяч см–1 (30 000 15 000 см–1). Колебательные переходы имеют частоты, на порядок и более отличающиеся от электронных в сторону уменьшения (2000 600 см–1). При квантовомеханическом рассмотрении молекулы обычно пользуются приближением Борна – Оппенгеймера, которое называют адиабатическим.
Оно основывается на различии масс электронов и ядер. Самое легкое ядро атома водорода в 1836 раз тяжелее электрона. Более легкие электроны движутся в молекуле значительно быстрее, чем ядра. За сравнительно малое время, порядка периода колебаний ядер, электроны в молекуле совершают несколько тысяч периодических движений. С точки зрения квантовой механики это будет означать, что фиксированному расположению ядер соответствуют определенные квазистационарные состояния, характеризуемые определенными значениями электронной энергии Ei. В отличие от атома, величина Ei не является строго постоянной, а зависит от расположения (конфигурации) ядер. Волновая функция, описывающая поведение электронов в поле фиксированных ядер, зависит не только от координат электронов, но и от координат ядер как медленно изменяющегося параметра, т. е. эл(r, R), где r означает координаты всех электронов, а R – всех ядер. Уравнение Шредингера для электронов в молекуле запишется в следующей форме:
элэл(r,R)=E(R)эл(r,R),
где оператор эл содержит дифференцирование по координатам электронов, т. е. кинетическую энергию только электронов, а все виды потенциальной энергии являются функцией R. Итак, электронная энергия молекулы не является постоянной характеристикой электронного состояния, а зависит от координат ядер. Графическое изображение этой зависимости называют потенциальной кривой. В случае многоатомной молекулы форма потенциальной кривой (это уже будет многомерная поверхность) достаточно сложна. Обычно при введении нормальных координат их число равно числу колебательных степеней свободы (n = 3 N – 6).
Для двухатомной молекулы имеется только одна колебательная степень свободы, характеризующая расстояние между ядрами, и кривая потенциальной энергии имеет простой вид (рис. 2.1и 2.2). На потенциальных кривых изображены колебательные подуровни нижнего и верхнего электронных состояний. Для простоты приведены только четыре колебательных подуровня. Внизу показан общий характер спектра поглощения двухатомной молекулы. Спектр хорошо передает колебательную структуру двухатомной молекулы, частота колебания которой рассчитывается по формуле классического осциллятора
где k – квазиупругая постоянная; – приведенная масса молекулы.
Наибольшая интенсивность приходится в спектре на полосу соответствующую переходу из нижнего колебательного подуровня = 0 на верхний колебательный подуровень = 1. Этому переходу соответствует наибольшее перекрытие волновых функций нижнего и верхнего состояний (принцип Франка-Кондона). Это переходы с неизменным межъядерным расстоянием молекулы, происходящие в моменты, когда скорости движения ядер равны нулю. Далее в ультрафиолетовую область интенсивность полос уменьшается практически по экспоненциальному закону.
в силу малости энергии вращательного движения разрешить вращательную структуру колебательных полос можно только с использованием приборов с высокой разрешающей способностью и только для молекул в газовой фазе.
Электронные спектры двухатомной молекулы в газовой фазе представляют собой совокупность полос, отвечающих электронно-колебательным переходам, в которых при высоком разрешении прослеживается вращательная структура. В случае многоатомной молекулы, состоящей из N атомов, колебательная струк тура отдельной электронной полосы значительно усложняется за счет увеличения числа колебательных
подуровней (рис. 2.3). В нелинейных многоатомных молекулах число колебательных подуровней равно числу колебательных степеней свободы. Отдельные электронно-колебательные полосы могут налагаться друг на друга, что приводит к их перекрытию и уширению. В зависимости от степени усложнения электронно-колебательных спектров все многоатомные молекулы условно подразделяют на простые (в спектре хорошо наблюдается колебательная структура), полусложные (в которых просматриваются следы колебательной структуры) и сложные, в которых полностью утрачивается колебательная структура и электронная полоса представляет собой бесструктурный куполообразный контур. К последним относится большое число органических соединений, широко представленных в природных объектах и имеющих разнообразные практические применения. При наличии в структурах таких молекул систем сопряженных связей (чередующиеся одиночные и двойные связи – C – C = C, ароматические циклы, гетероциклы с включением в кольцо атомов азота, кислорода и др.), а также разнообразных заместителей, включающих карбоксильные, карбонильные, гидроксильные аминогруппы и др., электронные полосы поглощения и испускания этих соединений располагаются в ультрафиолетовой, видимой и ближней ИК-областях, что делает их доступными для экспериментального изучения. С увеличением числа заместителей или сопряженных групп полосы поглощения и испускания обычно сдвигаются в низкочастотную область. Для разрешенных по спину переходов (S = 0) сечения поглощения составляют величины 10–18 10–16см2, а силы осцилляторов этих переходов находятся в пределах fосц 0,1 1,0.
На рис. 2.3 приведены уровни энергии сложной молекулы и возможные переходы между ними при поглощении света. Нижние электронные состояния обозначаются S0 , верхние – S1. Внизу приведен общий вид спектра поглощения сложной молекулы.
Спектры атомов и двухатомных молекул весьма индивидуальны. Каждой молекуле или атому соответствует свой весьма характерный спектр поглощения и испускания. Спектры сложных молекул также обладают некоторой индивидуальностью. Положение полос поглощения и испускания в шкале частот (или длин волн) различно. Однако эта индивидуальность весьма ограничена, вследствие бесструктурности электронных полос.
Единицы измерения энергии в спектроскопии
В оптическую спектроскопию входят ультрафиолетовая спектроскопия, спектроскопия видимого диапазона и инфракрасная спектроскопия. Ультрафиолетовая спектроскопия занимает диапазон 200 – 400 нм, видимая спектроскопия диапазон 400 – 650 нм и инфракрасная спектроскопия – от 650 нм (0,65 мкм) до 25 мкм. Границы диапазонов являются несколько условными, так как свойства излучения постепенно изменяются с изменением длины волны.
С точки зрения квантовой теории свет излучается или поглощается отдельными порциями энергии в соответствии с соотношением Бора
где Еk и Ei – энергии уровней, между которыми происходит переход;
h – постоянная планка, равная 6,626 10–27 эрг с (6,626 10–34Джс). разность энергий комбинирующих уровней пропорциональна частоте перехода – частоте поглощаемого или излучаемого света, измеряемой
в с–1. В этом случае шкала энергий пропорциональна шкале частот (в с–1). Однако в спектроскопии больше всего пользуются шкалой энергий, измеряемых волновыми числами . Волновое число характеризует число длин волн, приходящееся на единицу длины, что соответствует записи . Если длина волны измеряются в см, то волновое число в см–1 (в системе СГСМ). В системе СИ надо было бы пользоваться единицей, равной м+1. Однако пользуются давно устоявшейся системой обозначений в спектроскопии и значения энергии обозначают в единицах с–1 или см–1. Переход от одной системы измерения к другой легко осуществляется по соотношениям
где с – скорость света; – длина волны.
Из последнего выражения видно, что шкала энергий в длинах волн обратно пропорционально частоте в с–1 или в см–1. Во многих учебниках и монографиях можно встретить шкалы энергий, измеряемых в эВ или в абсолютных температурах. Под электрон-вольтом понимают энергию, которую приобретает электрон, проходя разность потенциалов в 1 В. Шкала абсолютных температур устанавливается согласно соотношению h = kT, где
k – постоянная Больцмана; T – температура, при которой энергия фотона данной частоты равна величине kT, являющейся мерой средней тепловой энергии. различные шкалы () связаны переводными множителями, приведенными в табл. 2.1.
Таблица 2.1
Переводные множители единиц измерения энергии
|
Единицы |
см–1 |
с–1 = Гц |
Дж |
эВ |
К |
|
1 см–1 |
1 |
3 1010 |
1,9 10 –23 |
1,24 10–4 |
1,44 |
|
с–1 = Гц |
3,34 10 –11 |
1 |
6,62 10–34 |
4,14 10–15 |
4,8 10–11 |
|
1 Дж |
5,03 10 22 |
1,511033 |
1 |
6,24 10 18 |
7,24 1022 |
|
1 эВ |
8065 |
2,4210 14 |
1,6 10–19 |
1 |
11605,4 |
|
1К |
0,69 |
2,081010 |
1,38 10–23 |
0,86 10–4 |
1 |
В обратных сантиметрах ультрафиолетовый диапазон занимает область 50 000 25 000 см–1, видимый диапазон – 25 000 15 400 см–1 и инфракрасный диапазон – 15 400 400 см–1. В дальнейшем будем широко пользоваться волновыми числами (cм–1), частотами в (c–1), длинами волн (нм) и электрон-вольтами эВ. При переходе от одной системы единиц измерения к другой необходимо пользоваться значениями коэффициентов, приведенных в табл. 2.1.
Распределение молекул по уровням энергии
Интенсивность линий или полос в спектрах поглощения и испускания зависит не только от вероятности переходов между уровнями энергии, но и от заселенности уровней, т. е. от того, сколько молекул находится на исходном уровне Еi при заданной температуре Т. Существует закон, установленный Больцманом, показывающий, как распределены молекулы по энергетическим уровням в условиях теплового равновесия. Число молекул на i-м уровне описывается экспоненциальной функцией вида
ni = С n exp(–Ei / kT),
где n – общее число молекул; С – постоянная, зависящая от температуры; Еi – энергия уровня; k – постоянная Больцмана; Т – абсолютная температура.
Понятие о люминесценции
Поглощение атомом энергии светового кванта не проявляется в изменении скорости атома как целого, но вызывает изменение в распределении электрических зарядов внутри него.
Согласно современной теории атом состоит из положительного ядра и облака электронов, общий заряд электронов, общий заряд которых в сумме равен заряду ядра. Таким образом, в целом атом нейтрален. Число электронов изменяется в зависимости от сложности атома и равно атомному номеру элемента в периодической системе Менделеева. Простейший атом атом водорода имеет только один электрон, сложные атомы могут иметь несколько десятков электронов. В этом случае электроны разделяются на слои, расположенные вокруг ядра. Слои распадаются на несколько электронных оболочек. Для того чтобы оболочка была устойчива, она должна состоять из определенного количества электронов.
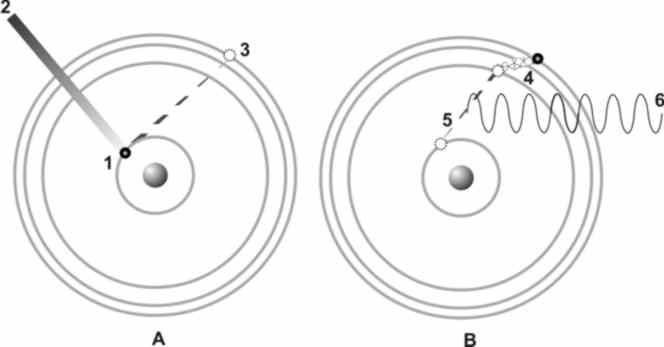
Рис.2.4.
На рис.2.4. показано как возникает люминесценция: на первом этапе (А) электрон (1) поглощает квант ультрафиолетового излучения (2), что переводит его на более высокий уровень энергии (3); затем (В), передав часть энергии кристаллу в виде тепла (4), электрон возвращается на исходный уровень (5), излучая остатки избыточной энергии в окружающее пространство в воде квантов света (6).
При увеличении атомного номера элемента заполнение электронных оболочек и слоев происходило в строгой последовательности. У более тяжелых атомов порядок заполнения оболочек несколько нарушается. В некоторых случаях первые оболочки высоких слоев заполняются ранее высоких оболочек низких слоев.
Видимое излучение люминесценция может возникнуть при поглощении атомом ультрафиолетовых или видимых лучей или при иных процессах, изменяющих расположение периферических электронов. Поглощение света внешним электроном изменяет положение и форму внешнего электронного облака и переводит атом в новое состояние, называемое возбуждением.
При поглощении света молекулой энергия поглощенного кванта частично расходуется на изменение конфигурации ее электронного облака, частично идет на изменение энергии колебаний ядер молекулы и изменении энергии ее вращения.
Для явлений люминесценции очень важны, однако, не чистые жидкости и не кристаллы с безупречно правильной решеткой, представляющей строгое повторение одних и тех же элементов, а растворы и кристаллы с решеткой, искаженной посторонними примесями. Эти инородные частицы и служат теми особыми местами вещества, которые являются источниками или носителями люминесценции. Однако их индивидуальные свойства, и прежде всего спектры поглощения и излучения, сильно изменяются, так как в общей массе жидкости или в поле кристаллической решетки они находятся под сильнейшим действием электрических зарядов окруженных частиц.
Переход молекулы в электронное возбужденное состояние может происходить не только при столкновении с быстро колеблющимися частицами, получившими энергию в процессе общего направления тела, но и многими другими путями, которые для этой цели применяются чаще и с большим удобством. Так, возбуждение молекулы наступает при поглощении кванта видимого или ультрафиолетового света, при соударении с электронами и иными быстро движущимися заряженными частицами, а также в ряде других случаев.
Возбужденные частицы обычно очень быстро, за время, измеряемое миллиардными долями секунды, теряют свою избыточную энергию и переходят в основное не возбужденное состояние. Такой переход может совершиться безызлучательно, путем передачи энергии окружающим частицам в виде тепла, или с излучением, которое и называется люминесценцией.
Таким образом, люминесценция это свечение, молекул, ионов и других более сложных компонентов, возникающее в результате электронного перехода в этих частицах при их возвращении из возбужденного состояния в нормальное (невозбужденное) за время большее периода световых колебаний.
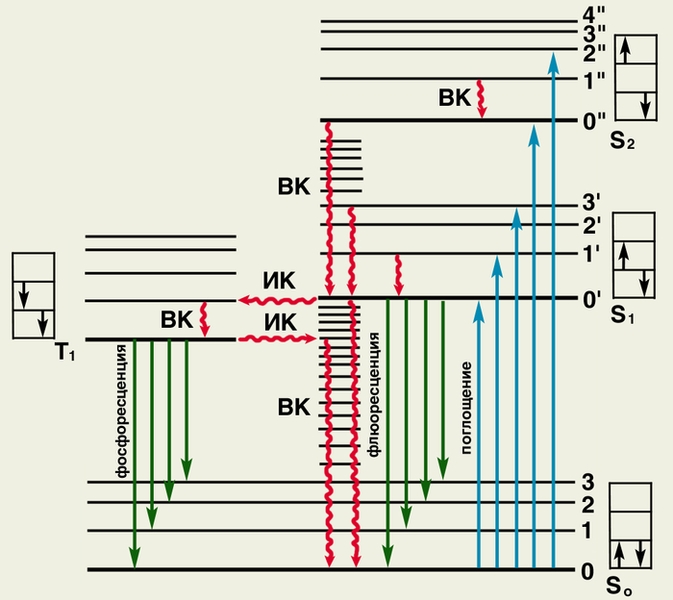
Рис.2.5.
На рис.2.5. показано схематическое изображение физического механизма люминесценции: жирными горизонтальными линиями обозначены энергетические состояния молекулы люминесцирующего вещества; S0 — основное (невозбужденное) состояние; S2, S2 и Т1 — возбужденные состояния; тонкими горизонтальными линиями обозначены колебательные уровни (0, 1, 2.,. или 0’, 1’, 2’ и т.д.); в прямоугольниках показано направление спина возбужденного электрона (слева) по отношению к спину оставшегося электрона; ВК — внутренняя конверсия (переходы электрона без обращения спина); ИК — интеркомбинационная конверсия (переходы электрона с обращением спина). При поглощении энергии молекула переходит в возбужденное состояние S1 или S2 (обозначено синими вертикальными стрелками). Часть поглощенной энергии преобразуется в тепло (обозначено волнистыми стрелками), при этом молекула переходит на нижний колебательный уровень состояния S1 или трансформируется в состояние Т1. Возвращение молекулы из состояния S1 или Т1 на исходный энергетический уровень может сопровождаться излучением света — флюоресценцией (обозначена темно-зелеными стрелками) или фосфоресценцией (обозначена светло-зелеными стрелками).
Характерные черты люминесценции.
В основание приведенного определения люминесценции положен характер элементарного процесса, протекающего в центре свечения. После излучения центр может оставаться в невозбужденном состоянии неопределенно долгое время, хотя не исключено, что он снова будет возбужден. В общем случае равновесия между внешним полем излучения и молекулами не предполагается, и тогда люминесценция является не равновесным процессом. Но в определенных частных случаях равновесие между состоянием поля излучения и молекулами может быть достигнуто, например, при равновесном температурном излучении, некоторые специфические свойства которого, связаны с его равновесным характером, нельзя распространять на все случаи люминесценции.
При исследовании люминесцентных явлений обычно наблюдается одновременное свечение огромного числа центров.
Поглощение энергии некоторое время остается в возбужденной люминесцентной частице. Это время определяется свойствами частицы и действиями внешней окружающей ее среды. Люминесценция вещества может характеризоваться длительностью возбужденного состояния, которое у частиц данного рода имеет вполне определенную среднюю величину, если они излучают в вакууме и не подвергаются действию окружающей среды.
Под действием внешнего поля и других частиц длительность возбужденного состояния может сократиться. Итак, люминесцентная частица является самостоятельным источником света, использующим поглощенную энергию, но преобразующим ее в собственное излучение. Эта важная особенность люминесценции отличает ее от несобственного излучения тела рассеяния и отражения веществом постороннего света.
Для возникновения свечения необходимо перевести частицы вещества в возбужденное состояние, т.е. ввести в них добавочный запас энергии, обеспечить для него условия достаточного длительного сохранения в молекуле, чтобы осуществился электронный переход и возращение центра в нормальное не возбужденное состояние. Последнее условие выполняется лишь в том случае, если возбужденные частицы обладают устойчивой конфигурацией электронного облака. Поэтому способность люминесцировать, присуща очень многим, но далеко не всем веществам.
В разряженном состоянии практически все газы обладают люминесцентной способностью и дают характерные спектры излучения в видимой и ультрафиолетовой области. Свечение чистых жидкостей обычно сильно потушено вследствие взаимодействия соседних частиц. Кроме того, у большинства органических веществ, но лежит в ультрафиолетовой области и недоступно непосредственному наблюдению глазом. Хорошо люминесцируют в видимой части спектра растворы многих солей: редкоземельных элементов, некоторых тяжелых металлов, ураниловых и платиносинеродистых соединений и т.д. Сильной люминесценцией обладают растворы многих органических соединений: ряда красителей, соединений ароматического рода и многих других органических соединений с сопряженными связями.
Перечисленные соединения хорошо люминесцируют и в кристаллических состояниях, особенно при низких температурах.
Люминесценцией обладают, и многие стекла в состав которых включены ионы люминесцентных веществ: уранила, редкоземельных элементов и др. По характеру спектров они близки к спектрам растворов соответствующих активаторов.
Квантовый и энергетический выходы
люминесценции
Под квантовым выходом люминесценции понимается отношение полного числа испущенных системой квантов к числу поглощенных за один и тот же промежуток времени в стационарном режиме возбуждения:
, (*)
В стационарном режиме число переходов с поглощением (например, в единицу времени) равно числу частиц, покидающих возбужденное состояние всеми путями, т.е. суммарному числу переходов с испусканием и безызлучательных переходов:
, (**)
Обозначим вероятность переходов с испусканием кванта света (т.е. излучательных), r вероятность безызлучательных переходов. Очевидно, что
,
r,
где n обозначена стационарная населенность возбужденного состояния.
Комбинируя (*) (**), получим выражение для квантового выхода:
,
Такое же выражение получается, если рассмотреть люминесценцию в режиме затухания и определить ее квантовый выход как отношение числа частиц, перешедших из возбужденного состояния излучательным путем, к полному числу частиц, покинувших возбужденное состояние всеми путями (т.е., находившихся в возбужденном состоянии в начальный момент времени). Действительно, если в начальный момент времени число частиц в возбужденном состоянии будет , то в момент времени t оно станет
,
Очевидно, число квантов, испускаемых в единицу времени, равно
,
Тогда общее число испущенных квантов будет
,
и квантовый выход
Так как время затухания люминесценции равно
,
a величина называется радиационным или излучательным временем жизни, получим
В соответствии с формулой квантовый выход может принимать значения в интервале от нуля до единицы. (Отметим при этом, что в рассматриваемой модели не принимается во внимание возможность реализации каскадных переходов с испусканием, в результате которых одному акту возбуждения может отвечать испускание двух или более фотонов с существенно меньшей энергией. В молекулярных системах с такими ситуациями практически не приходится сталкиваться, достаточно редко они встречаются в люминесценции примесных ионов в кристаллах).
Квантовый выход и время жизни флуоресценции существенно зависят от вероятности безызлучательных переходов . В величинувходят вероятности всех процессов, приводящих к опустошению возбужденного состояния , т.е. внутренней конверсией, интеркомбинационной конверсии и межмолекулярных процессов тушения люминесценции (тушение примесями, растворителем). Вероятности таких процессов могут быть записаны в виде произведения , где концентрация тушащих молекул, а характеризует «эффективность действия» молекул тушителя и называется бимолекулярной константой тушения. Таким образом,
В растворах во многих случаях дезактивация возбужденного состояния молекулы происходит с высокой вероятностью (близкой к единице) при каждой встрече молекулы тушителя с возбужденной молекулой. Термин «встреча» здесь употребляется сознательно, что бы отличить событие от простого сталкивания. Дело, в том, что в жидкости в отличие от газовой фазы, расхождению двух молекул (например, возбужденной молекулы и молекулы тушителя) после их встречи препятствуют окружающие молекулы растворителя, образующие «клетку» для сблизившихся молекул. В результате этого «эффекта клетки» на одну встречу, двух молекул может приходиться множество (десятки и сотни) столкновений. Даже если вероятность дезактивации в одном акте столкновения невелика, общая вероятность за множество столкновений, происходящих за одну встречу, может приближаться к единице. В таких случаях вероятность тушения определяется не специфическими характеристиками молекул тушителей, а только вероятностью встреч молекул, которая, в свою очередь, зависит от условий диффузии молекул в жидкости. Итак, в описанной ситуации говорят, что процесс тушения лимитируется диффузией, бимолекулярная константа скорости тушения может быть заменена на константу скорости встреч kc. Константа скорости встреч может быть получена из теории броуновской вращательной диффузии. В достаточно хорошо работающем приближении относительно крупных (в сравнении с размерами молекул растворителя) частиц в выражение для константы скорости встреч не входят размеры частиц, и оно имеет вид:
,
где Т температура, а вязкость в пуазах.
Обсуждаемые процессы тушения люминесценции, происходящие, когда молекула находится в электронно-возбужденном состоянии (ЭВС), называются (по С.И. Вавилову) процессами тушения второго рода.
Существует и иной класс процессов тушения процессы, при которых поглощение кванта света не приводит к возникновению ЭВС. Например, к люминесценции вследствии образования в основном состоянии комплекса с молекулой примеси, либо с такой же молекулой (комплексы молекул одного типа называется ассоциатами). Процессы такого типа называются процессами тушения первого рода или процессами неактивного поглощения.
Принимая их в расчет, можно переписать выражение для квантового выхода в виде
,
где доля молекул, поглотивших квант, но не перешедших в ЭВС.
С.И. Вавилов экспериментально установил закон: квантовый выход люминесценции молекул не зависит от частоты возбуждения во всем спектре поглощения, за исключением самой длинноволновой его части (антистоксово возбуждение), где он резко падает.
Причины независимости квантового выхода от длины волны возбуждения в целом те же, что причина независимости спектров люминесценции от длины волны возбуждения: процессы внутренней конверсии ВК21 и колебательной релаксации происходит значительно быстрее, чем переходы с флуоресценцией и безызлучательные из S1.
В отношении причин падения квантового выхода при длинноволновом возбуждении существует ряд веских аргументов в пользу того, что наблюдаемое в эксперименте падение не связано с какими либо принципиальными эффектами, а обусловлено, неактивным поглощением примесей и ассоциантов. Действительно, по мере переходов к возбуждению на длинноволновом краю полосы поглощения имеет место резкое падение коэффициента поглощения исследуемого вещества, поэтому даже присутствующие в малой концентрации не люминесцирующие примеси могут дать заметный вклад в регистрируемое общее поглощение.
Энергетический выход люминесценции Г определяется как отношение энергии испущенной системой люминесценции к энергии, поглощенной при возбуждении:
,
где и число испущенных и поглощенных квантов частоты в расчете на единичный интервал частот соответственно. Из этого выражения легко видеть, что в предельном случае монохроматической люминесценции энергетический выход может быть выражен через квантовый выход и частоты люминесценции и возбуждения:
Спектры люминесценции
Спектром люминесценции называют зависимость интенсивности люминесцентного излучения от длины волны возбуждающего её света. Наиболее простые — атомные спектры, в которых указанная выше зависимость определяется только электронным строением атома. Спектры молекул гораздо более сложные вследствие того, что в молекуле реализуются различные деформационные и валентные колебания. При охлаждении до сверхнизких температур сплошные спектры люминесценции превращаются в квазилинейчатые. Это явление получило название эффекта Шпольского. Это ведёт к снижению предела обнаружения и повышению избирательности определений, расширению числа элементов, которые можно определять люминесцентным методом анализа.
500 520 540 560 580 600 620 640 660 v10-12,ceк-1
600 577 551 535 517 500 483 469 455 ммк
Рис.2.6.
На рис.2.6. показаны спектры поглощения (абсорбации) и флуоресценции щелочного раствора флуоресцеина. По оси абсцисс отложены частоты колебаний, а по оси ординат величины, пропорциональные интенсивностям излучения. Кривая флуоресценции Ф и кривая поглощения (абсорбции) А.
Правило Стокса — Ломмеля
Первый закон люминесценции был установлен Стоксом в 1852 году, согласно которому длина волны излучения люминесценции всегда больше длины волны света, который поглощается и вызывает люминесценцию. Таким образом,
.
Такая люминесценция называется стоксовой. Позже было выявлено, что при фотолюминесценции также наблюдается излучение с длиной волны меньше длины волны света, вызывающего люминесценцию. Такое излучение, когда , называют антистоксовым. Ломмель дал новую, более общую формулировку: спектр флуоресценции в целом и его максимум всегда смещены по сравнению со спектром поглощения и его максимумом в сторону более длинных волн . В такой формулировке эту закономерность называют законом (правилом) Стокса — Ломмеля.
Закон Стокса — Ломмеля имеет очень общее значение. Он строго выполняется для большого количества веществ. Возникновение антистоксовой части спектра, для которой имеет место неравенство
,
не противоречит закону сохранения энергии. Возникновение квантов люминесценции, энергия которых превышает энергию квантов света, поглощенного веществом, вызвано тем, что молекулы вещества в невозбужденном состоянии обладают некоторым запасом колебательной энергии. Эта энергия вместе с энергией поглощенного кванта приводит к возникновению квантов люминесценции, удовлетворяющих условию (5). Таким образом, при возникновении антистоксовой части спектра люминесценции происходит частичная трансформация колебательной энергии молекул в энергию их излучения.
Правило зеркальной симметрии спектров
поглощения и люминесценции Левшина
Для некоторых классов органических молекул спектры поглощения и спектры люминесценции обладают зеркальной симметрией как по положению, так и по форме. Эту закономерность впервые в 1931 году сформулировал Левшин: спектры поглощения и люминесценции, построенные в шкале частот, размещаются зеркально симметрично относительно линии, проходящей через точку пересечения кривых обоих спектров. Важно то, в каких координатах строятся спектры поглощения и люминесценции. Блохинцев на основе квантовой теории обобщил правило зеркальной симметрии и показал, что если строить спектры люминесценции в координатах от , а спектр поглощения в координатах от в нормированном по максимуму виде, то точка пересечения кривых зеркально-симметричных спектров позволяет определить точное значение частоты чисто электронного перехода (рис. 6.4). Правило зеркальной симметрии можно записать в виде
,
где — частота поглощенного света; — симметричная ей частота в спектре люминесценции; — частота линии симметрии, проходящей через точку пересечения обоих спектров. Вместо выражения (6) можно записать:
.
Отсюда видно, что при строгом выполнении правила зеркальной симметрии спектров поглощения и люминесценции между величинами и имеет место линейная зависимость. Если на оси Ох откладывать , а на оси Оу — , то получим прямую линию с угловым коэффициентом, равным 2. Построение этой линейной зависимости является удобным методом проверки выполнения зеркальной симметрии спектров поглощения и люминесценции. Для выполнения правила зеркальной симметрии необходима симметрия частот и симметрия интенсивностей поглощения и люминесценции в соответствующих участках спектров. Чтобы выполнялось условие симметрии частот, необходимо, чтобы системы колебательных уровней невозбужденного и возбужденного состояний молекулы были одинаково построены и распределение молекул по ним было одинаковым.
Для выполнения зеркальной симметрии интенсивностей необходимо: 1) одинаковое распределение молекул по колебательным уровням в невозбужденном и возбужденном состояниях; 2) вероятности поглощательных и излучательных переходов между уровнями с одинаковыми номерами колебательных подуровней исходного и конечного состояний были пропорциональными или равными.
Универсальное соотношение Степанова
В 1956 году Б.И. Степановым был открыт общий закон, связывающий спектры поглощения и люминесценции сложных молекул. В соответствии с этим законом контуры полос поглощения и люминесценции сложных молекул связаны соотношением, которое получило название универсального:
, (***)
где D — постоянная, зависящая от температуры, условий возбуждения и ряда других факторов. Главное условие для выполнения универсального соотношения (***) заключается в том, чтобы установить равновесное распределение частиц по колебательным подуровням основного и возбужденного состояний за время, значительно меньшее времени спонтанного перехода. Условие (***) можно записать так:
и прологарифмировать (как предложил Аленцев):
.
Последнее выражение дает возможность экспериментально проверить выполнение универсального соотношения Степанова. Действительно, если построить график зависимости , то должна получиться прямая линия.
. (****)
По угловому коэффициенту этой прямой можно определить температуру среды (раствора) Т:
.
Линейный ход зависимости (****) практически наблюдается во всех опытах по проверке универсального соотношения. Однако температура Т, определенная по наклону прямой, временами не соответствует температуре раствора и чаще всего превышает ее. Это несоответствие поясняется на основе представлений о влиянии межмолекулярных взаимодействий на спектры молекул в растворах.
Типы возбуждения люминесценции
- Люминесценция, возбуждаемая электромагнитным излучением.
Рентгенолюминесценция. Специфика возбуждения рентгеновскими лучами, по сравнению с фото возбуждением, состоит в том, что на люминофор воздействуют фотоны со значительно большей энергией. При этом свечение люминофора вызывается не непосредственным действием самих рентгеновских лучей, в воздействием электронов, вырываемых из основы люминофора рентгеновскими лучами. Вследствие этого ретгенолюминесценция имеет многие общие черты с катодолюминесценцией.
Основное применение - в экранах для рентгеноскопии и рентгенографии.
- Люминесценция, возбуждаемая корпусным излучением.
Катодолюминесценция - возбуждается воздействием на люминофор потока электронов. Основное применение - визуализация электронного изображения на экранах телескопов телевизоров, осциллографов и других подобных приборов, а также электронно-оптических преобразователей.
Ионолюминесценция - свечение, возникающее при бомбардировке люминофора пучком ионов. При ионолюминесценции, также как при катодолюминесценции, энергия возбуждения поглощается в тонком приповерхностном слое люминофора, поэтому здесь оказывает состояние поверхности, в частности, хемосорбция различных газов.
Радиолюминесценция. Для создания самосветящихся красок постоянного действия, не нуждающихся в подточниках внешнего возбуждения, в люминофор вводят радиоактивные изотопы продукты распада которых (например, альфа и бета частиц) возбуждают в нем свечение. Время в течение, которого люминофор излучает свет, определяется периодом полураспада изотопа (десятки лет). Радиолюминесценция все более широко применяется в дозиметрии радиоактивных излучений.
- Люминесценция, возбуждаемая электрическим полем.
Электролюминесценция (эффект Дестрио). Многие кристаллические порошкообразные люминофоры, помещенные в конденсатор, питаемый переменным напряжением 100-220 В. с частотой 400-3000 Гц. начинают интенсивно. Люминесцировать. Спектральный состав и интенсивность излучения существенно зависят от частоты возбуждения. Некоторые люминофоры излучают и при возбуждении постоянным электрическим полем.
Инжекционная электролюминесценция (эффект Лосева). Свечение возникает под действием зарядов, инжектируемых в полупроводниковые кристаллы. При пропускании тока через полупроводниковый диод в области перехода инжектируются избыточные носители тока (электроны и дырки), рекомендация которых сопровождается оптическим излучением.
- Люминесценция, возбуждаемая за счет энергии химических реакций, называется хемилюсценцией.
Этим видом люминесценции объясняется свечение гнилушек, светлячков, многих глубоководных рыб. Хемилюсценция использована фирмой "Ремингтон АРМ-с" для создания лампы, в которой свечение возникает при воздействии кислорода воздуха на некоторые химически активные вещества.
Виды люминесценции
Резонансная люминесценция (чаще называется резонансной флуоресценцией) наблюдается в атомных парах (ртути, натрия и др.) у некоторых простых молекул и, иногда, в более сложных системах. Излучение имеет спонтанный характер и происходит с того же энергетического уровня, которые достигаются при поглощении энергии возбуждающего света. При повышении плотности паров резонансная люминесценция переходит в резонансное рассеяние.
Этот вид свечения по всех случаях не должен относиться к люминесценции и должен называться резонансным рассеянием.
Спонтанная люминесценция включает переход (излучательный или, чаще, безызлучательный) на энергетический уровень, с которого происходит излучение. Этот вид люминесценции характерен для сложных молекул в парах и растворах, и для примесных центров в твердых телах. Особый случай представляет люминесценция, обусловленная переходами из экситонных состояний.
Метастабильная или вынужденная люминесценция характеризуется происходящим после поглощения энергии переходом на метастабильный уровень и последующим переходом на уровень излучения в результате сообщения колебательной энергии (за счет внутренней энергии тела) или дополнительного кванта света, например инфракрасного. Пример этого вида люминесценции — фосфоресценция органических веществ, при которой метастабилен нижний триплетный уровень органических молекул. При этом, во многих случаях наблюдается две полосы длительности люминесценции: длинноволновая, соответствующая спонтанному переходу T-S0 и затем (медленная флюоресценция или -полоса), и коротковолновая, совпадающая по спектру с флюоресценцией и соответствующая вынужденному переходу T-S1 и затем спонтанному переходу s1- s0 (фосфоресценция или -полоса).
Рекомбинационная люминесценция происходит в результате воссоединения частиц, разделившихся при поглощении возбуждающей энергии. В газах может происходить рекомбинация радикалов или ионов, в результате которой возникает молекула в возбужденном состоянии. Последующий переход в основное состояние может сопровождаться люминесценцией. В твердых кристаллических телах рекомбинационная люминесценция возникает в результате появления неравновесных носителей заряда (электронов или дырок) под действием какого- либо источника энергии.
Литература
Агранович В. М. Перенос энергии электронного возбуждения в конденсированных средах. /В. М. Агранович, М. Д. Галанин. М., 1978.
Гайсенок В. А. Анизотропия поглощения и люминесценции многоатомных молекул. /В. А .Гайсенок, А. М. Саржевский. Минск., 1986.
Гулис И. М. Лазерная спектроскопия. /И. М. Гулис. Минск., 2002.
Ермолаев В. Л. Безызлучательный перенос энергии электронного возбуждения. /В. Л. Ермолаев [и др.] Л.: 1977.
Комяк А. И. Молекулярная спектроскопия. / А. И. Комяк. Минск., 2005.
Лакович Дж. Основы флуоресцентной спектроскопии. /Дж. Лакович. М.: Мир, 1986.
Левшин Л. В. Люминесценция и ее измерения. Молекулярная люминесценция. /Л. В. Левшин, А. М. Салецкий М., 1989.
Саржевский А. М. Анизотропия поглощения и испускания света молекулами. /А. М. Саржевский, А. Н. Севченко Минск., 1971.
Степанов Б. И. Введение в современную оптику. Поглощение и испускание света квантовыми системами. Минск.: 1991.
Степанов Б. И., Введение в теорию люминесценции /Б. И. Степанов,
В. П. Грибковский Минск., 1963.
Паркер С. Фотолюминесценция растворов. /С. Паркер М., 1972.
PAGE \* MERGEFORMAT 25
Рис. 2.1. Колебательные функции для комбинирующих
электронно-колебательных уровней.
Наиболее интенсивный переход
= 0 = 1
EMBED Equation.DSMT4 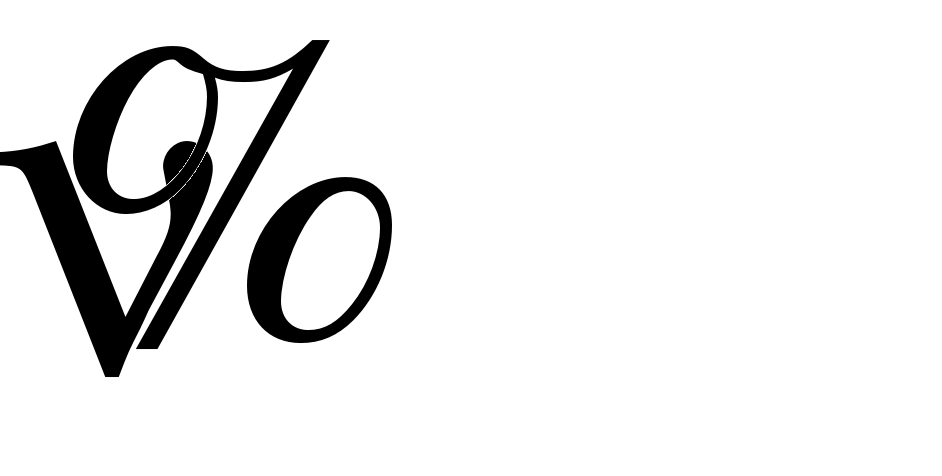 , см–1
, см–1
EMBED Equation.DSMT4 
1,0
0
,5
20000
22000
0
1
2
3
4
0
1
2
3
4
кол(q)
кол(q)
V(q)
q
q0
, нм
400
500
600
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
S0
S1
EMBED Equation.DSMT4 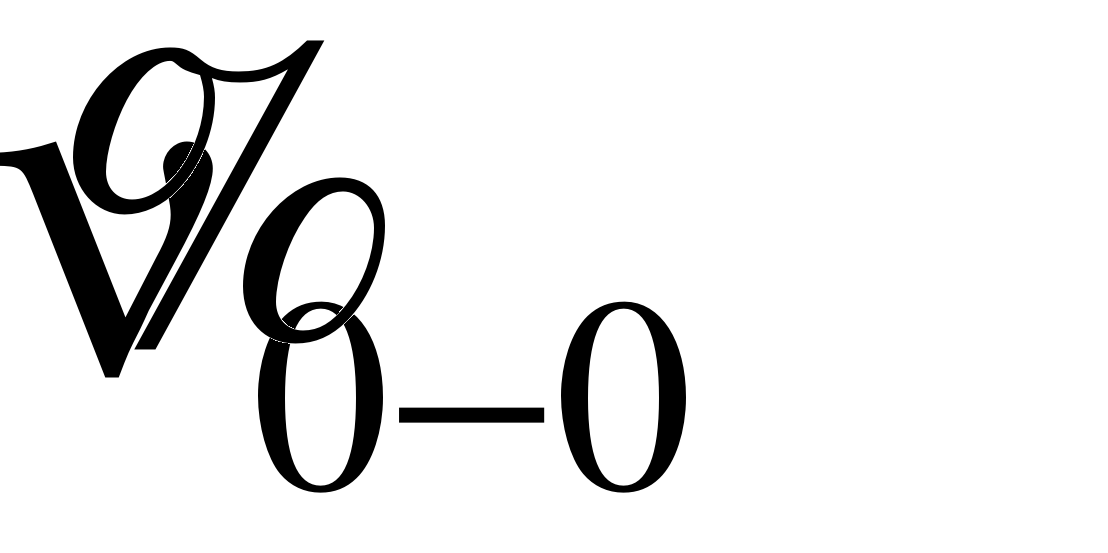
Рис. 2.3 уровни энергии сложной
молекулы и возможные переходы между ними при поглощении света. Нижние электронные состояния обозначаются S0 ,
верхние – S1. Внизу приведен общий вид спектра поглощения сложной молекулы.
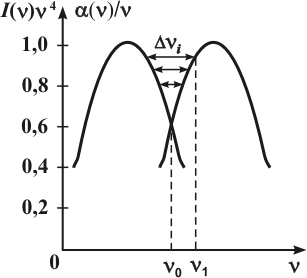
Рис. 6.4. Зеркальная симметрия
полос поглощения и люмине-
сценции
1
0
2
3
0
0
0
0
0
1
1
2
2
2
2
2
1
1
1
3
3
3
3
3
0–0
0–0
0–0
V(r)
V(r)
EMBED Equation.3 
EMBED Equation.3 
V(r)
Рис. 2.2. Наиболее вероятные колебательные переходы при различном сдвиге равновесного расстояния в верхнем возбужденном состоянии.
а – сдвиг отсутствует. Наиболее вероятный переход '' = 0' = 0. б – относительно небольшой сдвиг. Наиболее вероятный переход '' = 0' = 1.
в - Сравнительно большой сдвиг. Наиболее вероятный переход '' = 0' = 2
EMBED Equation.3  0-0
0-0
EMBED Equation.3 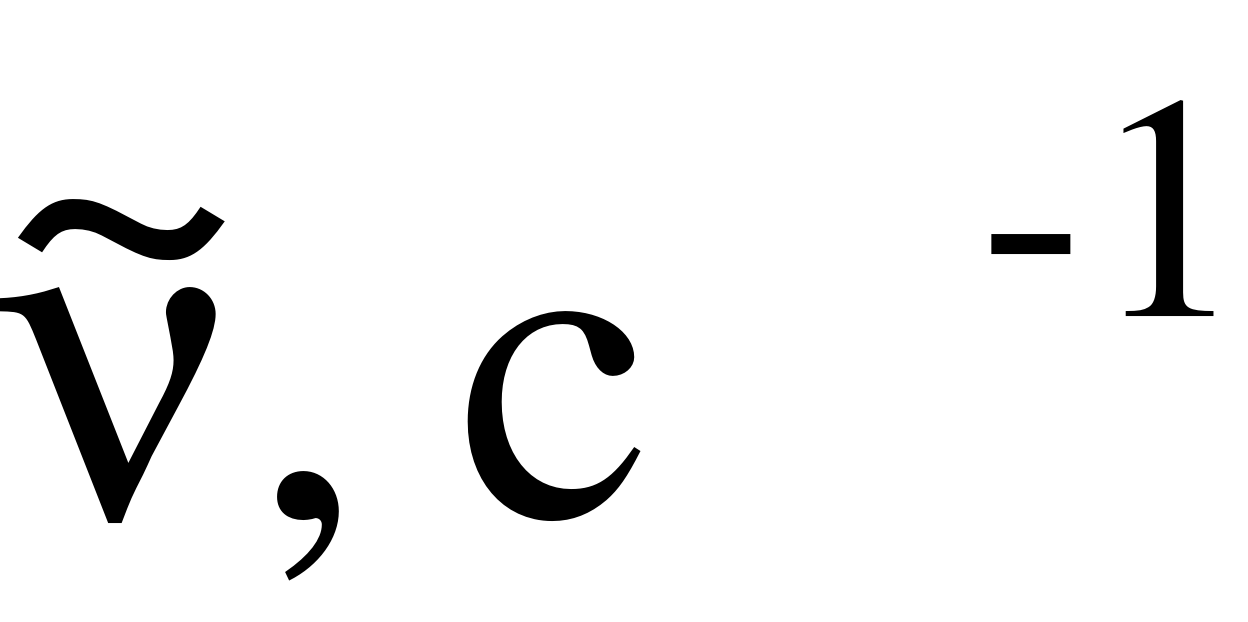 0-0
0-0
EMBED Equation.3 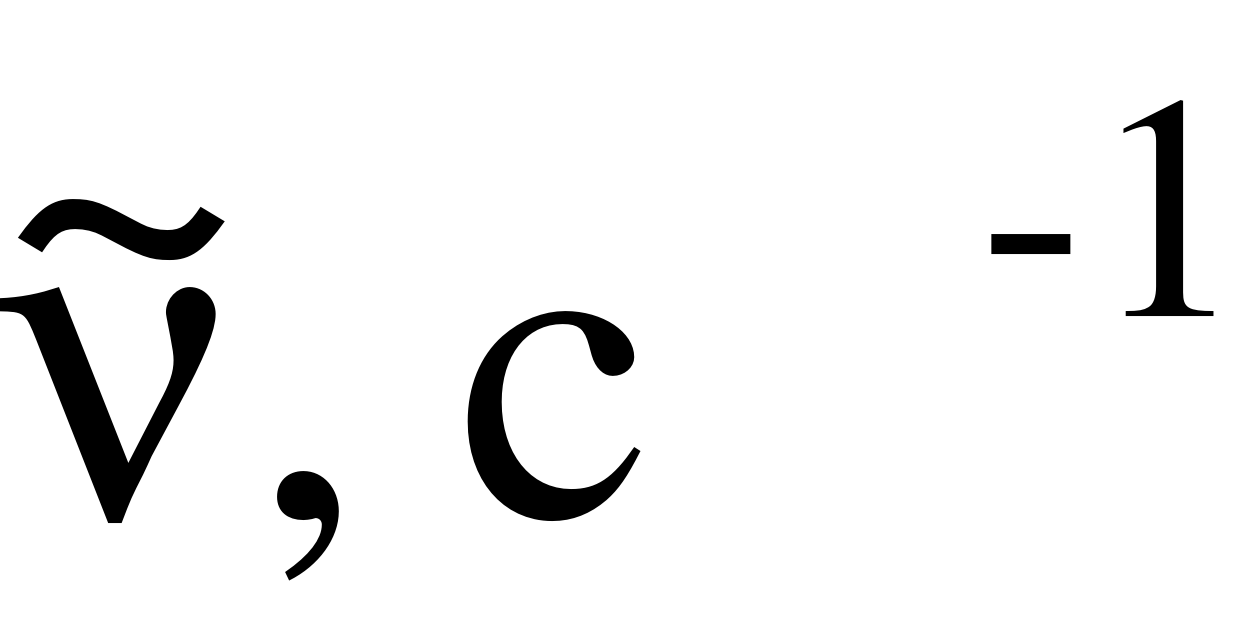 0-0
0-0
EMBED Equation.3 
а
б
в
Электромагнитное излучение и вещество