Математическое планирование эксперимента для проведения регрессионного анализа

В современных условиях, учитывая многогранность изучаемых явлений, острый дефицит времени, высокую стоимость эксплуатации научного оборудования, необходимо стремиться к наиболее рациональным планам проведения эксперимента.

Во многих случаях полученное по результатам эксперимента уравнение регрессии используется как математическая модель объекта. Математические модели объекта могут быть детерминированными и статистическими.

Детерминированные математические модели объекта, строят на основе фундаментальных законов физики, механики, химии и других естественных наук. Статистические математические модели получают, описывая зависимости выходных параметров yz (свойств, откликов) объекта от изменения входных параметров xj (факторов) с помощью различных функций:

yz = v(x1, x2, x3, ..., xj, ..., xk) + (w1, w2, w3, ..., wv, ...) ,

где - вклад в изменение свойств объекта случайных факторов.

Наиболее часто в качестве статистической модели объекта используют приближенные уравнения регрессии

yz = fz(x1, x2, x3, ..., xj, ..., xk) + + .

Одно из основных требований к математической модели объекта - это точность описания (прогнозирования) поведения реального объекта при изменении значений факторов xj.

Применение методов математического планирования эксперимента для проведения регрессионного анализа (РАМПЭ) может помочь получить уравнения регрессии, более точно описывающего реальный объект (с меньшими ошибками + ), чем уравнение полученное при КРА. В некоторых случаях применение методов математического планирования эксперимента позволяет значительно сократить числа опытов.

В основу методов математического планирования эксперимента для проведения РА положен принцип "черного ящика". Суть этого принципа заключается в том, что исследователь, не зная об истинных закономерностях поведения объекта, описывает его с помощью статистических математических моделей.

Образно говоря, "ударяя" по исследуемому объекту изменением входных параметров (xj) в ходе эксперимента (рис. 6) и измеряя его реакцию (yz) на эти "удары" при действии случайных факторов (wv), можно получить статистическую математическую зависимость, пригодную для прогноза поведения объекта.

Рис. 6. Схема объекта по принципу "черного ящика"

С помощью метода "черного ящика" получают статистические математические модели объектов в виде полиномов различной степени.

Известно, что любую функцию (в том числе ) можно разложить в ряд Тейлора и представить в виде конкретного полинома определенной степени (конечного отрезка ряда Тейлора) вида:

…,

где и b - соответственно генеральные коэффициенты ряда Тейлора.

По результатам эксперимента возможно определить вид полинома только с выборочными коэффициентами ряда Тэйлора,

где: b0 - величина y при нулевом значении всех факторов (свободный член);

b1, b2, ..., bj, ..., bk - линейные эффекты влияния соответствующих факторов на величину y;

b12, b13, ..., b1j, ...,b1k, b23, b34, ..., b2j, ..., b(k-1)j, ..b(k-1)k - парные эффекты влияния соответствующих факторов на величину y (эффекты "взаимодействия" двух соответствующих факторов);

b11, b22, ..., bjj, ..., bkk - квадратичные эффекты влияния соответствующих факторов на величину y;

b123, b124, ..., b1uj, ..., b234, b235, ..., b2uj, ..., b(k-2)(k-1)k - тройные эффекты влияния соответствующих факторов на величину y (эффекты "взаимодействия" трех соответствующих факторов) и т.д.

Наиболее удобно планировать эксперимент математическими методами для кодированных значений факторов (xj), получаемых из натуральных значений (Xj) по следующим формулам:

; ; ,
где - натуральное значение фактора в центре (середине) выбранной (заданной) области изменения (варьирования) фактора, и - соответственно максимальное и минимальное значения фактора в выбранной области его изменения, Хj - шаг варьирования фактора. В соответствии с этими формулами натуральному значению Xj = соответствует кодированное значение xj = 0; Xj = - кодированное значение xj = +1, а Xj = - значение xj = -1.

Переход от кодированных значений факторов к натуральным осуществляют по формуле

Выбор плана эксперимента для применения РАМПЭ, в отличие от планирования экспериментов для проведения КРА, определяется видом выбранного семейства функций (видом полинома).

После завершения эксперимента для проведения РАМПЭ выполняют следующие действия:

Выбирают вид полинома (отрезок ряда Тейлора) для поиска уравнения регрессии.

Для выбранного полинома с помощью МНК рассчитывают параметры функции (выборочные коэффициенты уравнения регрессии).

Проверяют рассчитанные выборочные коэффициенты уравнения регрессии на значимость (равенство нулю).

Корректируют вид исходной функции, исключая из нее незначимые коэффициенты и другие составляющие.

Оценивают ошибки, допускаемые при описании истинной зависимости с помощью найденного уравнения регрессии: проверяют адекватность уравнения регрессии с помощью распределения Фишера или рассчитывают вероятность описания зависимости функцией f.

Если точность найденного уравнения регрессии не удовлетворяет, то выбирают, планируют и реализуют другой план эксперимента для поиска уравнения регрессии в другом семействе полиномов (например, полиномов более высокого порядка).

Порядок проведения РАМПЭ в отличие от КРА имеет следующие особенности:

Выбирается только один класс функций - полиномы.

Используется только один метод приближения - МНК.

После корректировки уравнения регрессии его коэффициенты не пересчитываются.

Выполняется меньшее количество этапов РА.

Обычно поиск уравнения регрессии начинают в семействе самых простых полиномов: первого и второго порядка. По названиям степеней полиномов называют и планы эксперимента для применения РАМПЭ.

Прежде чем перейти к знакомству с методами математического планирования эксперимента для применения регрессионного анализа, необходимо отметить некоторые важные обстоятельства:

1. С познавательной точки зрения полиноминальная статистическая модель объекта не представляет большого интереса. Зная оценки коэффициентов отрезков ряда Тейлора, нельзя определить истинную зависимость , а следовательно, невозможно получить информацию о механизме поведения исследуемого объекта.

Полиноминальные модели справедливы только для условий, в которых проводился эксперимент.

3. Полиноминальные модели очень полезны с практической точки зрения, так как позволяют управлять поведением объекта и решать для него задачи оптимизации.

7.4.3.2.2.1. Планы первого порядка

Планы первого порядка позволяют находить линейные уравнения регрессии (I) и нелинейные уравнения (II) с членами, учитывающими эффекты "взаимодействия" факторов:

; (I)

+ b123 x1x2x3 + b124x1x2x4+ ...+ b(k-2) (k-1) k x k-2 x k-1 x k . (II)

Для удобства программирования расчетов в состав уравнения регрессии вводят фиктивную переменную х0 = +1 во всех опытах эксперимента:

;

Для РАМПЭ наибольшее распространение получили двухуровневые (mj = m =2) ортогональные D-оптимальные планы первого порядка типа 2(k-a). При таких планах все факторы в кодированном виде могут иметь только два значения (xj = +1 и xj = -1). Тип плана обозначает формулу для расчета числа его опытов без их повторения (N): N = m(k-a) = 2(k-a), где k > a, и а равно 0,1, 2, 3, ...

При а = 0 план типа 2(k-a) является планом ПФЭ типа 2k, а при а > 0 - планом ДФЭ.

Планы, отвечающие условиям ортогональности, позволяют любой коэффициент уравнения регрессии рассчитывать по одной формуле:

где i - номер опыта в плане эксперимента; bd - коэффициент, учитывающий эффект факторов, значения которых приведены в столбце xd плана эксперимента; yi - свойства объекта, измеренные при проведении соответствующего опыта; N - число опытов в эксперименте.

D-оптимальные планы обеспечивают минимальную и одинаковую ошибку в оценке всех коэффициентов уравнения регрессии (), определяемую по формуле

где - дисперсия воспроизводимости, характеризующая случайные ошибки всего эксперимента.

Условием ортогональности плана эксперимента является выполнение условия

= 0 при u j и u,j равных 0, 1, 2, ..., k.

Для D- оптимальных планов должны выполняться следующие условия:

при j равном 1, 2, ..., k;

= N при j равном 0, 1, 2, ..., k.

Выбор плана эксперимента начинается с расчета необходимого числа опытов (Nнеобх.) или его задания (Nзад.). При этом должны выполняться соотношения

N Nнеобх. ; Nнеобх. k + 1 ; Nнеобх. L + 1; Nзад. N,

где L - общее число коэффициентов в выбранном семействе полиномов (число отрезков ряда Тейлора).

При расчете Nнеобх. задаются видом полинома (типом и числом коэффициентов уравнения регрессии L), а при задании числа опытов определяют вид семейства полиномов, в котором возможно найти уравнение регрессии для данного числа опытов в эксперименте:

kmax = Nзад. - 1; Lmax = Nзад. -1.

Рассмотрим возникающие задачи выбора линейного плана на примере.

Допустим, что мы решили исследовать влияние на свойство y четырех факторов xj (k = 4) и описать их зависимость уравнением регрессии в виде следующего нелинейного полинома (L = 11):

+ b14 x1x4 + b23x2x3 + b24x2x4 + b34x3x4.

Тогда совместное выполнение соотношений даст:

Nнеобх. k + 1 4+1 5; Nнеобх. L + 1 11+1 12; Nнеобх. 12.

Очевидно, что соотношению N Nнеобх отвечают планы типа 2(k-а) при условии, что (k-a) 4 и соответственно N 16. Из совокупности планов с N 16 выберем план ПФЭ типа 24 как наиболее экономный по числу опытов (N = 16) и позволяющий получить наиболее точные оценки коэффициентов уравнения регрессии. При ПФЭ все выборочные коэффициенты уравнения регрессии являются достаточно точными, "несмешанными" оценками соответствующих генеральных коэффициентов: bd d.

Для построения ортогонального и D-оптимального плана ПФЭ типа 24 воспользуемся одним из распространенных приемов, заключающемся в следующем:

Делается заготовка плана в виде таблицы (плана-матрицы эксперимента), в которой предусматривается не менее N строк и (Lmax +2) столбца для хd.

В первый столбец таблицы заносят номера строк, соответствующие номерам опытов. Во второй столбец - кодированные значения фиктивного фактора х0 (во всех строках плана х0 = + 1). В третий столбец - кодированные значения первого фактора (х1) в виде последовательного чередования друг за другом значений (+1) и (-1). В последующем, четвертом столбце для х2, выбранная комбинация чередований в предыдущем столбце знаков (+1) и (-1) удваивается, например: после двух знаков (+1) следуют два знака (-1). По аналогичному принципу удвоения комбинации чередования знаков предыдущего столбца заполняются и последующие столбцы для всех оставшихся факторов.

Столбцы для оценки эффектов "взаимодействия" факторов (х12, х13, х23 и др.) заполняются путем перемножения знаков для соответствующих факторов в соответствующих строках таблицы (х12 = х1х2, х13 = х1х3 и т.д.).

Правильность составления плана проверяется по выполнению условия его D- оптимальности .

Построенный по этому приему план приведен в табл. 16.

Таблица 16

План ПФЭ типа 24

Но-	Кодированные значения факторов	y
мер опыта i	х0	х1	х2	х3	х4	х12	х13	х14	х23	х24	х34
1	+1	+1	+1	+1	+1	+1	+1	+1	+1	+1	+1
2	+1	-1	+1	+1	+1	-1	-1	-1	+1	+1	+1
3	+1	+1	-1	+1	+1	-1	+1	+1	-1	-1	+1
4	+1	-1	-1	+1	+1	+1	-1	-1	-1	-1	+1
5	+1	+1	+1	-1	+1	+1	-1	+1	-1	+1	-1
6	+1	-1	+1	-1	+1	-1	+1	-1	-1	+1	-1
7	+1	+1	-1	-1	+1	-1	-1	+1	+1	-1	-1
8	+1	-1	-1	-1	+1	+1	+1	-1	+1	-1	-1
9	+1	+1	+1	+1	-1	+1	+1	-1	+1	-1	-1
10	+1	-1	+1	+1	-1	-1	-1	+1	+1	-1	-1
11	+1	+1	-1	+1	-1	-1	+1	-1	-1	+1	-1
12	+1	-1	-1	+1	-1	+1	-1	+1	-1	+1	-1
13	+1	+1	+1	-1	-1	+1	-1	-1	-1	-1	+1
14	+1	-1	+1	-1	-1	-1	+1	+1	-1	-1	+1
15	+1	+1	-1	-1	-1	-1	-1	-1	+1	+1	+1
16	+1	-1	-1	-1	-1	+1	+1	+1	+1	+1	+1

Нетрудно проверить, что данный план является ортогональным и D-оптимальным.

План с натуральными значениями факторов Xj строится исходя из плана с кодированными значениями путем замены знаков (+1) и (-1) на соответствующие им натуральные значения для данного фактора.

Довольно часто на практике приходится задаваться не видом полинома, а числом опытов из-за дефицита ресурсов для проведения эксперимента (времени, средств и др.). В этом случае выбор плана эксперимента начинают с расчета параметров полинома, которые возможно определить при Nзад..

Допустим, что Nзад. = 10, k = 4 и уравнение регрессии необходимо получить в следующем виде (L = 5):

Оценим возможности двухуровнего плана первого порядка с N = 10:

kmax = Nзад. - 1= 10-1= 9;

Lmax = Nзад. -1= 10-1= 9.

Из данных равенств следует, что план с 10 опытами позволяет решить нашу задачу и оценить влияние четырех факторов (k < kmax) по уравнению регрессии в виде полинома с числом коэффициентов равным 5.

При Nзад. = 10 возможна реализация только плана ДФЭ, так как план ПФЭ для четырех факторов насчитывает 16 опытов: 2k = 24 = 16.

Воспользуемся методом дробных реплик для построения планов ДФЭ типа 2(k-a). Наиболее близким по числу опытов к Nзад. = 10 является полуреплика (1/2 часть) плана ПФЭ, т.е. план ДФЭ типа 2(4-1) с числом опытов N = 8. Проверка показывает, что план типа 2(4-1) пригоден для решения поставленной задачи, так как выполняются следующие соотношения:

N k + 1 4+1 5;

N L + 1 5+1 6.

Поскольку план ДФЭ представляет собой часть опытов плана ПФЭ, то необходимо решить, какой именно набор опытов из плана ПФЭ использовать в плане ДФЭ. От этого набора будет зависеть точность определения эффектов влияния факторов на свойство y (так называемая "смешиваемость" коэффициентов).

Построение планов ДФЭ начинают по тому же приему, что и при построении планов ПФЭ для числа факторов, равных разности (k-а). В нашем случае k-a = 4-1 = 3.

Поэтому построим первоначально заготовку плана ДФЭ типа 2(4-1) в виде плана ПФЭ типа 23, предусмотрев в нем (Lmax +2 = 9+2 = 11) колонок (табл. 17).

При заполнении столбца для фактора х4 принцип удвоения чередований уровней, применяемый для построения планов ПФЭ, не подходит, так как его использование в данном столбце даст только знаки (+1) и такой план не будет являться ортогональным. Если же для заполнения столбца х4 воспользоваться произведением двух и более других факторов в одной строке плана (так называемым генерирующим соотношением), то тогда план будет и ортогональным и D- оптимальным.

К выбору генерирующего соотношения нужно подходить осознанно, так как оно определяет "смешанность" (точность) коэффициентов уравнения регрессии, полученных по составленному плану.

Составим и проанализируем все возможные варианты генерирующего соотношения для х4:

х4 = х1х2 (I); x4 = x1x3 (II); x4 = x2x3 (III); x4 = x1x2x3 (IV).

Для данных генерирующих соотношений рассчитаем определяющие контрасты путем умножения левой и правой частей соответствующего генерирующего соотношения на х4:

; ; ; .

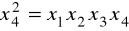Так как х4 = 1, то всегда и определяющие контрасты можно выразить равенствами:

1 = х1х2х4 (I); 1 = х1х3х4 (II); 1 = x2x3x4 (III); 1 = x1x2x3x4 (IV).

Таблица 17

Заготовка плана ДФЭ типа 2(4-1)

Но-	Кодированные значения факторов	y
мер опыта i	х0	х1	х2	х3	х4
1	+1	+1	+1	+1
2	+1	-1	+1	+1
3	+1	+1	-1	+1
4	+1	-1	-1	+1
5	+1	+1	+1	-1
6	+1	-1	+1	-1
7	+1	+1	-1	-1
8	+1	-1	-1	-1

Перемножив левые и правые части определяющих контрастов на каждый фактор можно определить в плане столбцы с одинаковым порядком чередования знаков (+1) и (-1), например для фактора х1:

; ;

; .

Эти равенства показывают, что при генерирующих соотношениях I-IV выборочный коэффициент b1 будет служить оценкой влияния на y не только фактора x1, но и других:

b1 1 + 24 (I) ; b1 1 + 34 (II); b1 1 + 1234 (III); b1 1 + 234 (IV).

Эффекты "взаимодействия" трех и более факторов обычно близки к нулю и ими можно пренебрегать [8]:

b1 1 + 24 (I) ; b1 1 + 34 (II); b1 1(III); b1 1(IV).

Поэтому можно считать, что "несмешанные" оценки эффекта влияния фактора x1 на свойство y могут быть получены при реализации плана ДФЭ с генерирующими соотношениями III и IV для фактора х4. Результаты проверки на "смешиваемость" остальных эффектов приведены в табл. 18.

Данные табл. 18 показывают, что при любом генерирующем соотношении точными ("несмешанными") будут пять коэффициентов. Для генерирующего соотношения I точными будут все коэффициенты, оценивающие эффект фактора х3, при II - эффект фактора х2, при III - эффект фактора х1, а при IV - линейные эффекты всех факторов.

Так как по заданию нам необходимо получить уравнение регрессии с линейными эффектами всех факторов и эти эффекты должны быть наиболее точными, то выбираем генерирующее соотношение IV и в соответствии с ним заполняем колонку плана для х4 (табл. 19).

Таблица 18

Параметры проверки разрешающей силы дробной реплики типа 2(4-1)

Параметр	Выражение для определения параметра
Генерирующее соотношение	x4 = x1x2 (I)	x4 = x1x3 (II)	x4 = x2x3 (III)	x4 = x1x2x3 (IV)
Определяющий контраст	1 = x1x2x4	1 = x1x3x4	1 = x2x3x4	1 = x1x2x3x4
Оценки коэффициентов уравнения регрессии	b0 0+124 b1 1 + 24 b2 2 + 14 b3 3 + 1234 b4 4 + 12 b12 12+4 b13 13+234 b14 14+2 b23 23+134 b24 24+1 b34 34+123	b0 0+134 b1 1 + 34 b2 2 + 1234 b3 3 + 14 b4 4 + 13 b12 12+234 b13 13+4 b14 14+3 b23 23+124 b24 24+123 b34 34+1	b0 0+234 b1 1 + 1234 b2 2 + 34 b3 3 + 24 b4 4 + 23 b12 12+134 b13 13+124 b14 14+123 b23 23+4 b24 24+3 b34 34+2	b0 0+1234 b1 1 + 234 b2 2 + 134 b3 3 + 124 b4 4 + 123 b12 12+34 b13 13+24 b14 14+23 b23 23+14 b24 24+13 b34 34+12
Примечание. Жирным шрифтом выделены "несмешанные" коэффициенты

Этот план, с N = 8, является ортогональным и D-оптимальным. По данному плану есть возможность оценить еще 6 эффектов парного влияния факторов, однако, как показывают данные табл. 18, расчеты приведут к получению "смешанных" коэффициентов уравнения регрессии (т.е. неточно отражающих парное влияние соответствующих факторов), так как комбинациями знаков (изменения значений факторов) совпадают у х14 и х23, х13 и х24 и др.

Два дополнительных опыта (опыты № 9 и № 10) можно использовать как повторные для оценки дисперсии воспроизводимости эксперимента, если сделать допущение, что и другие опыты плана имеют такие же случайные ошибки. Дисперсия воспроизводимости () по результатам этих двух опытов может быть использована для оценки ошибки в определении коэффициентов уравнения регрессии и их значимости, а также проверки адекватности найденного уравнения регрессии.

В соответствии с общепринятыми рекомендациями запланируем опыты для определения при нулевых кодированных значениях всех исследуемых факторов, т.е. в центре области изменения факторов (табл. 19).

Таблица 19

План ДФЭ типа 2(4-1) с генерирующим соотношением x4 = x1x2x3

Но-	Кодированные значения факторов	y
мер опыта i	х0	х1	х2	х3	х4	х12 и х34	х13 и х24	х14 и х23
1	+1	+1	+1	+1	+1	+1	+1	+1
2	+1	-1	+1	+1	-1	-1	-1	+1
3	+1	+1	-1	+1	-1	-1	+1	-1
4	+1	-1	-1	+1	+1	+1	-1	-1
5	+1	+1	+1	-1	-1	+1	-1	-1
6	+1	-1	+1	-1	+1	-1	+1	-1
7	+1	+1	-1	-1	+1	-1	-1	+1
8	+1	-1	-1	-1	-1	+1	+1	+1
9	+1	0	0	0	0	0	0	0
10	+1	0	0	0	0	0	0	0

В качестве планов первого порядка для проведения РАМПЭ можно использовать не только дробные реплики ПФЭ, но и некоторые другие планы ДФЭ, например планы ПлакеттаБермана.

Следует только еще раз повторить, что прежде, чем использовать планы ДФЭ, необходимо оценить потерю точности в определении эффектов влияния факторов на свойство объекта.

Алгоритмы расчетов при РАМПЭ по планам первого порядка зависят от наличия повторений опытов. Познакомьтесь с ними самостоятельно [8].

После реализации плана эксперимента первого порядка довольно часто найденное уравнение регрессии оказывается неадекватным. В этом случае обычно переходят к выполнению РАМПЭ для поиска уравнения регрессии в семействе полиномов второго порядка по результатам специально спланированных экспериментов.

PAGE 78

Математическое планирование эксперимента для проведения регрессионного анализа