ПЛАНИРОВАНИЕ И АНАЛИЗ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

ВВЕДЕНИЕ

С философской точки зрения аспиранты занимаются научным познанием.

Предлагаемая вам для изучения дисциплина освещает достаточно подробно только один из методов эмпирического исследования - эксперимент. При этом мы обязательно будем обращаться и к измерению и наблюдению.

Необходимость изучения данной дисциплины аспирантами УГЛТУ связана с тем, что при получении высшего образования по некоторым специальностям и направлениям в соответствии с действующими образовательными стандартами либо не изучаются основы научных исследований, либо их изучение проводится в объеме не достаточном для качественного выполнения диссертационного исследования.

Цель дисциплины - приобретение аспирантами дополнительных знаний, практических навыков и умений самостоятельной работы по планированию и анализу результатов эксперимента.

Задачи дисциплины:

изучение аспирантами современных представлений и опыта планирования, проведения и анализа результатов эксперимента;

оказание практической помощи аспирантам в планировании, проведении и анализе результатов собственных научных исследований на современном уровне.

Рекомендуемая литература:

1. Глебов И.Т., Глухих В.В., Назаров И.В. Научно-техническое творчество: Учеб. пособие. - Екатеринбург: УГЛТУ, 2002. - 264 с.

2. Гоберман В.А., Гоберман Л.А. Технология научных исследований. Методы, модели, оценки: Учебное пособие. 2-е издание стереотипное. – М.: МГУЛ, 2002. – 390 с.

ОБЩИЕ ПРЕДСТАВЛЕНИЯ ОБ ЭКСПЕРИМЕНТЕ

Эксперимент [1] – наиболее важный и сложный метод эмпирического познания. Под экспериментом понимается такой метод изучения объекта, когда исследователь активно воздействует на него путем создания искусственных условий, необходимых для выявления соответствующих свойств данного объекта.

Эксперимент предполагает использование наблюдения, сравнения и измерения как более элементарных методов исследования. Главная особенность эксперимента заключается во вмешательстве экспериментатора в течение естественных процессов, которое обуславливает активный характер данного метода познания.

Эксперимент позволяет исследовать явления в "чистом" виде, когда побочные факторы исключаются. Можно исследовать свойства объектов в экстремальных условиях (при сверхнизких или сверхвысоких температурах, при высоком давлении, в условиях невесомости и др.). Это может привести к неожиданным эффектам.

Установлено, что чем больше используется в науке эксперимент, тем быстрее она развивается.

Экспериментальные исследования (эксперимент) в различных отраслях науки состоят из следующих обязательных элементов, выполняемых в следующей последовательности:

Целями эксперимента могут быть:

исследование процессов, происходящих в исследуемом объекте;

определение характеристик объекта;

проверка результатов теоретического исследования;

получение исходных данных для теоретических исследований и др.

Планирование эксперимента подразделяют на две части: методическую и организационную.

В методической части анализируют, составляют и выбирают план и методику проведения эксперимента, выбирают средства измерения, экспериментальные образцы, материалы, установки, исследователей.

В организационной части решают вопросы материально-технического обеспечения эксперимента (подготовку к работе средств измерения, установок, исследователей и др.).

Выбор плана эксперимента зависит от:

целей и задач НИР и эксперимента;

методов анализа результатов эксперимента, которые планируется применить;

объема имеющихся материальных ресурсов (финансовых, человеческих и др.);

временных ресурсов (ограничений на время научных исследований) и др.

Как уже отмечалось выше, в эксперименте используется такой элементарный акт эмпирического исследования, как измерение. Поэтому для улучшения взаимопонимания остановлюсь на некоторых аспектах и особенностях измерения.

ИЗМЕРЕНИЯ

Напомню, что измерением называется определение значения искомой величины путем сравнения ее с эталоном.

Как следует из определения измерения, его результатом являются единичные значения измеряемой величины (первичные данные).

Результаты измерений могут иметь качественный или количественный вид. Качественные значения обычно выражаются словами. Количественные значения - числами.

Пример. Вы измеряли свой рост. Результат измерения можно выразить качественным значением (средний, ниже среднего, выше среднего, низкий, нормальный, высокий и др.). В этом случае за эталон Вы приняли рост какого-то человека. Можно представить результат измерения роста и количественным числовым значением, если за эталон Вы выбрали какой-нибудь эталон меры (мм, см, м и др.).

Представление и обработка количественных результатов измерений имеют значительные особенности.

Особенности представления и обработки количественных результатов измерений

1. Характеристика результатов измерений как случайных величин

Результаты измерений относятся к случайным числам. Под случайной величиной понимают величину, принимающую значение, которое нельзя точно предсказать (классический пример - появление цифры на верхней грани игрового кубика). Случайная величина имеет набор допустимых значений, но в каждом конкретном случае принимает только одно значение из этого набора. Это значение может быть различным при попытке повторения из-за действия случайных (неизвестных или неконтролируемых) факторов. Набор допустимых значений недостаточен для полной характеристки случайной величины. Необходимо еще указывать вероятность (частоту появления) каждого конкретного значения из этого набора.

Наиболее полной характеристикой любой случайной величины является закон ее распределения. Закон распределения случайной величины - это соотношения между возможными значениями случайной величины и соответствующими им вероятностям. Закон распределения случайной величины может быть представлен графически, в виде таблицы или математической функции (интегральная или дифференциальная функция распределения), из которых можно определить вероятность (Р) появления конкретных значений случайной величины.

Различают дискретные и непрерывные случайные величины. Примером случайной дискретной величины может быть число аспирантов, присутствующих на лекции (это число, которое может принимать только целочисленное значение кратное единице). Примером непрерывной случайной величины является масса тела человека, которая может принимать любое значение.

Известно много законов распределения случайных величин. Наиболее часто для непрерывных величин встречаются экспоненциальное и нормальное распределение (распределение Гаусса). На нормальном распределении базируются распределения хи-квадрат (Пирсона), Стьюдента, Фишера и др.

Для дискретных величин может наблюдаться биномиальное распределение, распределение Пуассона и др.

Математические выражения законов распределения имеют достаточно сложный вид. На практике наиболее часто пользуются табличными и графическими формами законов распределения.

Примеры (слайд):

Закон распределения выпавших очков при бросании

шестигранного игрового кубика

Значение	1	2	3	4	5	6
Вероятность	1/6	1/6	1/6	1/6	1/6	1/6

Закон распределения выпавших очков при бросании

двух шестигранных игровых кубиков

Значение	2	3	4	5	6	7	8	9	10	11	12
Вероятность	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

Интегральная функция нормального распределения случайной величины, F(х).

F (x) = P(X<x), где Р - вероятность появления значения Х для случайной величины; х -произвольно задаваемое действительное число.

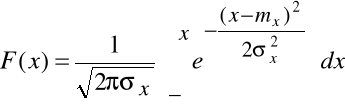
Дифференциальная функция нормального распределения случайной величины, (x)

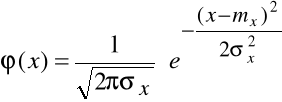
(x) = dF(x)/dx (- < x < )

Результаты любого количественного измерения всегда являются случайными величинами, так как невозможно исключить все ошибки измерения. Поэтому количественные результаты измерений, при наличии возможности, необходимо характеризовать параметрами математической статистики.

Знание закона распределения позволяет рассчитать некоторые параметры результатов измерений.

Для расчета параметров результатов измерений используют методы математической статистики.

2. Представление результатов измерений с учетом их погрешностей

Под погрешностью измерения будем понимать совокупность всех ошибок измерения.

2.1. Ошибки измерений

Ошибки измерений можно классифицировать по следующим видам:

Абсолютные и относительные.

Положительные и отрицательные.

Постоянные и пропорциональные.

Случайные и систематические.

Прочие (грубые, допустимые, возможные предельные ошибки и др.)

Абсолютная ошибка единичного результата измерения (Аy) определяется как разность следующих величин:

Аy = yi - yист. yi -y,

где: yi - единичный результат измерения; yист. - истинный результат измерения; y - среднее арифметическое значение результата измерения (далее среднее).

Если абсолютная ошибка измерения не зависит от значения измеряемой величины (y y ), то такая ошибка называется постоянной. В противном случае ошибка будет пропорциональной. Характер ошибки измерения (постоянная или пропорциональная) определяется после проведения специальных исследований.

Относительная ошибка единичного результата измерения (Вy) рассчитывается как отношение следующих величин:

Из этой формулы следует, что величина относительной ошибки зависит не только от величины абсолютной ошибки, но и от значения измеряемой величины. При неизменности измеряемой величины (y) относительную ошибку измерения можно уменьшить только за счет снижения величины абсолютной ошибки (Аy). При постоянстве абсолютной ошибки измерения для уменьшения относительной ошибки измерения можно использовать прием увеличения значения измеряемой величины.

Знак ошибки (положительный или отрицательный) определяется разницей между единичным и полученным (средним арифметическим) результатом измерения:

yi -y > 0 (ошибка положительная);

yi -y < 0 (ошибка отрицательная).

К случайным ошибкам относят ошибки, которые не имеют постоянной величины и знака. Такие ошибки возникают под действием следующих факторов: неизвестных исследователю; известных, но нерегулируемых; постоянно изменяющихся.

Случайные ошибки можно оценить только после проведения измерений.

Количественной оценкой модуля величины случайной ошибки измерения могут являться следующие параметры: выборочная дисперсия единичных значений и среднего значения; выборочные абсолютные стандартные отклонения единичных значений и среднего значения; выборочные относительные стандартные отклонения единичных значений и среднего значения; генеральная дисперсия единичных значений (соответственно ) и др.

Случайные ошибки измерения невозможно исключить, их можно только уменьшить. Один из основных способов уменьшения величины случайной ошибки измерения - это увеличение числа (объема выборки) единичных измерений (увеличение величины n). Объясняется это тем, что величина случайных ошибок обратно пропорциональна величине n, например:

Систематические ошибки - это ошибки с неизменными величиной и знаком или изменяющиеся по известному закону. Эти ошибки вызываются постоянными факторами. Систематические ошибки можно количественно оценивать, уменьшать и даже исключать.

Систематические ошибки классифицируют на ошибки I, II и III типов.

К систематическим ошибкам I типа относят ошибки известного происхождения, которые могут быть до проведения измерения оценены путем расчета. Эти ошибки можно исключить, вводя их в результат измерения в виде поправок. Примером ошибки такого типа является ошибка при титрометрическом определении объемной концентрации раствора, если титрант был приготовлен при одной температуре, а измерение концентрации проводилось при другой. Зная зависимость плотности титранта от температуры, можно до проведения измерения рассчитать изменение объемной концентрации титранта, связанное с изменением его температуры, и эту разницу учесть в виде поправки в результате измерения.

Систематические ошибки II типа - это ошибки известного происхождения, которые можно оценить только в ходе эксперимента или в результате проведения специальных исследований. К этому типу ошибок относят инструментальные (приборные), реактивные, эталонные и др. ошибки. Познакомьтесь с особенностями таких ошибок самостоятельно.

Любой прибор при его применении в процедуре измерения вносит в результат измерения свои приборные ошибки. При этом часть этих ошибок случайная, а другая часть - систематическая. Случайные ошибки приборов отдельно не оценивают, их оценивают в общей совокупности со всеми другими случайными ошибками измерения.

Каждый экземпляр любого прибора имеет свою персональную систематическую ошибку. Для того чтобы оценить эту ошибку, необходимо проводить специальные исследования.

Наиболее надежный способ оценки приборной систематической ошибки II типа - это сверка работы приборов по эталонам. Для мерной посуды (пипеток, бюреток, цилиндров и др.) проводят специальную процедуру - калибровку.

На практике наиболее часто требуется не оценить, а уменьшить или исключить систематическую ошибку II типа. Самыми распространенными методами уменьшения систематических ошибок являются методы релятивизации и рандомизации. Познакомьтесь с этими методами самостоятельно.

К ошибкам III типа относят ошибки неизвестного происхождения. Эти ошибки можно обнаружить только после устранения всех систематических ошибок I и II типов.

К прочим ошибкам отнесем все другие виды ошибок, не рассмотренные выше (допустимые, возможные предельные ошибки и др.).

Грубая ошибка измерения (промах) возникает при нарушении методики измерения. Результат измерения, содержащий грубую ошибку, обычно значительно отличается по величине от других результатов. Наличие грубых ошибок измерения в выборке устанавливается только методами математической статистики (при числе повторений измерения n>2). С методами обнаружения грубых ошибок познакомьтесь самостоятельно.

Понятие возможных предельных ошибок применяется в случаях использования средств измерения и предполагает максимально возможную по величине инструментальную ошибку измерения (реальное же значение ошибки может быть меньше величины возможной предельной ошибки).

При использовании средств измерения можно рассчитать возможные предельные абсолютную (Пy,пр. ) или относительную (Еy,пр. ) погрешности измерения. Так, например, возможная предельная абсолютная погрешность измерения находится как сумма возможных предельных случайных (y, случ., пр.) и неисключенных систематических (y, пр.) ошибок:

Пy,пр. = y, случ., пр. + y, пр.

При выборках малого объема (n 20) неизвестной генеральной совокупности, подчиняющейся нормальному закону распределения, случайные возможные предельные ошибки измерений можно оценить следующим образом:

y, случ., пр. = y = SytP, n,
где: y - доверительный интервал для соответствующей вероятности Р; tP,n - квантиль распределения (критерий) Стьюдента для вероятности Р и выборки объемом n.

Абсолютная возможная предельная погрешность измерения в этом случае будет равна:

Пy,пр. = SytP, n+ y,пр.

Если результаты измерений не подчиняются нормальному закону распределения, то оценка погрешностей проводится по другим формулам.

Определение величины y,пр. зависит от наличия у средства измерения класса точности. Если средство измерения не имеет класса точности, то за величину y,пр. можно принять минимальную цену деления шкалы (или ее половину) средства измерения. Для средства измерения с известным классом точности за величину y,пр. можно принять абсолютную допустимую систематическую ошибку средства измерения (y, доп.):

y,пр. .

Величина y, доп. рассчитывается исходя из формул, приведенных в табл.

Для многих средств измерения класс точности указывается в виде чисел а10n , где а равно 1; 1,5; 2; 2,5; 4; 5; 6 и n равно 1; 0; -1; -2 и т.д., которые показывают величину возможной предельной допускаемой систематической ошибки (Еy, доп.) и специальных знаков, свидетельствующих о ее типе (относительная, приведенная, постоянная, пропорциональная).

Таблица

Примеры обозначения классов точности средств измерения

Обозначение класса точности	Формула расчета и значение предельной допускаемой систематической ошибки	Характеристика систематической
в документации	на средстве измерения		ошибки
Класс точности 1,5	1,5		Приведенная допускаемая систематическая ошибка в процентах от номинального значения измеряемой величины, которое определяется типом шкалы средства измерения [10]
Класс точности 1	1		Приведенная допускаемая систематическая ошибка в процентах от длины использованной шкалы средства измерения (А) при получении единичных значений измеряемой величины
Класс точности 0,5	0,5		Постоянная относительная допускаемая систематическая ошибка в процентах от полученного единичного значения измеряемой величины
Класс точности 0,02/ 0,01	0,02/0,01	c = 0,02 и d = 0,01	Пропорциональная относительная допускаемая систематическая ошибка в долях от полученного единичного значения измеряемой величины, которая возрастает при увеличении конечного значения диапазона измерения данным средством измерения (yk) или уменьшении единичного значения измеряемой величины (yi)

Общая погрешность единичного измерения состоит из систематической и случайной погрешностей измерения. В состав систематической погрешности измерения входят все систематические ошибки измерения, а в состав случайной погрешности - все случайные ошибки измерения. Например состав абсолютной погрешности единичного измерения можно представить следующим образом (слайд):

Если известны составляющие абсолютной систематической ошибки, например, среднего арифметического результата измерения (ошибка средства измерения, ошибка метода и др.), то ее можно оценить по формуле:

где: m - число составляющих систематическую ошибку среднего результата измерения; k - коэффициент, определяемый вероятностью Р и числом m; () - абсолютная систематическая ошибка отдельной составляющей.

Оценка погрешностей измерения зависит не только от условий измерения, но и от типа измерения (прямое это измерение или косвенное).

Деление измерений на прямые и косвенные достаточно условно. В дальнейшем под прямыми измерениями будем понимать такие, когда измеряемое значение находят непосредственно в опытных данных, например считывается со шкалы прибора (широко известный пример прямого измерения - измерение температуры с помощью термометра). К косвенным измерениям будем относить такие, когда результат измерения получают на основании известной зависимости между искомой величиной и величинами, определяемыми в результате прямых измерений. При этом результат косвенного измерения получают расчетным путем как значение функции (), аргументами которой являются результаты прямых измерений (x1, x2, …, xj,.…, xk).

Необходимо знать, что ошибки косвенных измерений всегда больше, чем ошибки отдельных прямых измерений.

2.2. Законы накопления ошибок косвенных измерений

Ошибки косвенных измерений оцениваются по соответствующим законам (при k 2).

Закон накопления случайных ошибок косвенных измерений выглядит следующим образом:

; .

Закон накопления возможных предельных абсолютных систематических ошибок косвенных измерений представляется следующими зависимостями:

; .

Закон накопления возможных предельных относительных систематических ошибок косвенных измерений имеет следующий вид:

;

В случаях, когда искомая величина (y) рассчитывается как функция результатов нескольких независимых прямых измерений вида , закон накопления предельных относительных систематических ошибок косвенных измерений принимает более простой вид:

; .

Ошибки и погрешности измерений определяют их точность, воспроизводимость, сходимость и правильность.

Чем меньше величина погрешности измерения, тем выше его точность.

Более подробно с теорией ошибок измерений и их особенностями познакомьтесь самостоятельно. Обращу ваше внимание на то, что современные формы представления конечных результатов измерений обязательно требуют приведения ошибок или погрешностей измерения (вторичных данных). При этом погрешности и ошибки измерений должны представляться числами, которые содержат не более двух значащих цифр.

2. Формы представления конечных результатов измерений

Для представления количественных результатов измерений (при неизвестных параметрах генеральной совокупности) можно использовать следующие формы.

При одном единичном значении результата измерений

(n = 1):

y = y1 y,пр. .

2. При наличии нескольких единичных результатов измерений
(n 2) и отсутствии сведений о функции их распределения:

y = y ; Sy ; n ; y,пр. (может дополнительно еще приводиться значение вероятности Р, если расчет y,пр. носил вероятностный характер;

3. При наличии нескольких единичных результатов измерений
(n 2) и знании функции их распределения:

а) y =y Пy ; P (при симметричной погрешности);

б) y =y ; Пy от Пy, н до Пy, в; P (для несимметричной погрешности, где Пy, н - нижняя граница общей абсолютной погрешности, а Пy, в - верхняя граница общей абсолютной погрешности).

При окончательном представлении фактического результата измерения число значащих цифр и разрядов после десятичной запятой должно быть скорректировано исходя из точности математических вычислений и погрешности измерения.

Приведу пример обработки первичных данных измерения с целью получения и представления конечного результата измерения.

Пример. При трехкратном взвешивании образца на аналитических весах (класс точности 0,01 ) были получены следующие единичные неисправленные результаты измерения его массы (mi ): 1,2356; 1,2345; 1,2348 г. Результаты метрологической поверки весов свидетельствуют об их постоянной абсолютной систематической ошибке m = - 0,0003 г (для примененной гирьки из разновесов массой 1 г систематическая ошибка была равной нулю). Тогда ряд исправленных единичных результатов измерения массы образца (mi) будет иметь вид: 1,2359; 1,2348; 1,2351 г.

Первоначально проведем поиск грубых ошибок измерения (промахов). Так как для данной выборки n < 8 (n = 3), то согласно [6, с. 82-84] для обнаружения промахов используем Q-критерий. Единичные результаты измерений представим в виде нового ряда с возрастающими величинами массы образца: 1,2348; 1,2351; 1,2359 г. Проверим на промахи крайние члены этого нового ряда, которые кажутся сомнительными:

1. mn (проверяемый результат) = 1,2359 г ; mn-1 (результат соседний с проверяемым) = 1,2351 г ; R (размах) = 1,2359 - 1,2348 = 0,0011 г ;

Из данных табл.1 [6, с.82] выбираем табличное значение Q-критерия (QТ) для n = 3 и Р = 0,95 (принимаем наиболее часто задаваемое значение вероятности в химии и химической технологии). Так как

QТ > QР (0,94 > 0,73), то проверяемый результат (1,2359 г) не является грубой ошибкой измерения.

2. mn = 1,2348 г ; mn-1 = 1,2351 г ;

И этот проверяемый результат (1,2348 г) не является промахом, так как QТ > QР (0,94 > 0,27).

Так как истинный закон распределения результатов измерений неизвестен, то для представления конечных результатов измерения выберем форму 2. Выполним следующие расчеты, применяя правила математических действий и округления с приближенными и случайными числами:
г ; (г)2 ;
г ;

10-4 г ;

Делаем допущение, что систематическая ошибка весов намного превосходит прочие систематические ошибки, которыми можно пренебречь. Тогда:

m,пр. = = Еm m;
Еm = 0,0110-2 (исходя из обозначения класса точности весов).

m,пр. = 0,0110-2 1,2353 =1,235310-4г.

Поскольку , то систематическими ошибками можно пренебречь. Тогда:
Пm,пр. Sm 3,291410-4 310-4 г (в ошибках оставляю один первый разрядов цифр).

Таким образом, по форме 2б результат измерения массы образца будет выглядеть следующим образом:

m = 1,2353 г ; Sm = 310-4 г ; n = 3 ; P = 0,95.

ЭКСПЕРИМЕНТ

С особенностями планирования и анализа результатов экспериментальных исследований при создании новых объектов техники познакомьтесь самостоятельно по литературе [2]:

Я вас буду более детально знакомить с планированием и анализом результатов эксперимента на примере создании новых веществ, материалов, разработке новых технологий. У кого в диссертации не планируется проведение эксперимента предлагаю за объект взять создание нового торта.

В таких научных исследованиях наиболее часто при выполнении НИР целью экспериментальных исследований является получение математической модели объекта. Математическую модель объекта представляют в виде математической зависимости свойства изучаемого объекта (условно обозначим его y ) от значений факторов (xj ), влияющих на эти свойства:

y = (x1, x2, ..., xj, ...xk ) + ,

где - величина, не зависящая от xj ( назовем ее случайной величиной).

Выбор плана эксперимента зависит от того, какой вид зависимости вы желаете получить: качественный или количественный.

Зависимость является качественной, если она выражается словами, например: " xj влияет на y", " увеличение xj уменьшает значение y" и др.

Зависимость является количественной, если она представляет собой математическое выражение.

Так как результаты измерений значений xj и y являются случайными величинами, то для установления зависимости необходимо использовать соответствующие методы математической статистики.

Для получения качественной зависимости наиболее часто используют методы корреляционного и дисперсионного анализов, для получения количественной зависимости - метод регрессионного анализа. Производными от этих методов являются другие методы: ковариационного, кластерного, факторного анализов и др.

Планирование эксперимента для применения к его результатам корреляционного анализа

1. Общие положения корреляционного анализа

Корреляционный анализ - это один из наиболее простых методов математической статистики, позволяющий качественно предсказывать изменения y при изменяющихся значениях xj (устанавливать связь между этими случайными величинами).

Если каждому значению xj соответствует всегда строго определенное значение y, то считают, что между этими величинами существует функциональная связь, т.е. зависимость является функциональной. При наличии и знании такой связи можно точно предсказывать величину y, задавая конкретное значение xj.

Однако на практике функциональные связи обнаруживаются очень редко, поскольку на все результаты измерений оказывают влияние различные случайные факторы.

В большинстве случаев, задавая конкретное значение xj, можно предсказать лишь тенденцию изменения y. Эта тенденция обнаруживается лишь при достаточно большом числе mj различных значений (уровней) изменяемого фактора xj, а при малых величинах mj данная тенденция может не наблюдаться (рис. 3).

Рис. 3. Влияние числа значений х (m) на тенденцию изменения y:

1 - тенденция изменения y при m = 8,

2 - тенденция изменения y при m = 3

Связь между y и x, представленная на рис. 3, называется корреляционной (стохастической). Чем больше корреляционная связь соответствует функциональной связи, тем более тесной (сильной) она считается.

Корреляционная связь имеет два крайних предельных случая: функциональная связь (самая тесная зависимость y от xj) и полное отсутствие связи (влияния xj на y ).

Наличие между y и xj корреляционной или функциональной связи устанавливается только в результате проведения корреляционного анализа.

При корреляционном анализе отражают следующие выводы в форме слов:

Наличие связи между y и xj ("есть" или "нет" и др.)

Характер связи ("функциональная" или "корреляционная") и ее тип ("линейная", "нелинейная", "экспоненциальная", "параболическая", "синусоидальная" и др.)

Знак связи: "положительная" - если с увеличением величины значений xj растет величина y ; "отрицательная" - если с уменьшением величины значений xj снижается величина y.

Теснота (сила) корреляционной связи ("очень тесная", "тесная", "не очень тесная", "ярко выраженная", "выраженная", "слабо выраженная" и др.)

Корреляционный анализ проводят двумя методами: анализом поля корреляции и анализом коэффициента линейной корреляции.

2. Анализ поля корреляции (визуальный анализ)

Полем корреляции называют рисунок (график), выполненный на плоскости в системе двух прямоугольных координат y и х, на котором приведены точки с координатами yv и xv (V - номер уровня фактора х от 1 до m). Пример поля корреляции одного свойства объекта (y) и одного фактора (х) приведен на рис. 3.

Анализ поля корреляции проводится визуально. Для облегчения анализа рекомендуется весь массив точек с координатами yv и xv ( на рис. 3 приведены точки с координатами y1 и х1, y2 и х2, y3 и х3, ..., yv и хv, ..., y8 и х8) обвести замкнутым контуром. Характер этого контура помогает более точно сделать все выводы корреляционного анализа, например, чем больше контур приближается к форме окружности, тем выше вероятность того, что нет связи между y и x.

Метод анализа поля корреляции не является достаточно точным в основном из-за влияния на вид поля корреляции выбранного масштаба координатных осей y и x. Однако при корреляционном анализе это единственный метод определения характера нелинейной связи между y и х.

3. Анализ выборочного коэффициента парной линейной корреляции

Этот метод является более точным при установлении линейной корреляции между y и xj, так как он основан не на визуальном восприятии графического представления случайных чисел, а на математических расчетах и постулатах.

Рассмотрим самый простой случай: корреляцию между двумя случайными величинами (y и х).

Присвоим каждой точке на поле корреляции свой номер i (такой же номер будет и у взаимосвязанной пары координат этой точки). Обозначим N общее число точек с координатами yi и xi. Тогда выборочный коэффициент парной корреляции можно рассчитать по формуле

гдеy - общее среднее арифметическое значение y; x - общее среднее арифметическое значение х; Sx и Sy - выборочные абсолютные стандартные отклонения соответственно х и y (эти параметры используются как характеристики рассеивания единичных значений х и y относительно их общих средних арифметических значений).

Общие средние арифметические значения находят по формулам

; .

Выборочные абсолютные стандартные отклонения х и y можно рассчитать следующим образом:

; .

Выборочный коэффициент парной корреляции имеет следующие свойства:

Величина ryx не изменяется при изменении начала отсчета величин, а также масштаба координатных осей y и х.

В величине ryx одновременно заложена доля случайности и нелинейности связи между y и х.

По величине и знаку ryx можно сделать большинство выводов корреляционного анализа (табл. 6). Однако выводы корреляционного анализа можно делать только после доказательств равенства или отличия от нуля рассчитанного значения ryx методами математической статистики (так называемая статистическая проверка нуль-гипотезы). С методами проверки нуль-гипотезы ryx познакомьтесь самостоятельно.

Как следует из табл. 6, значение ryx позволяет сделать все выводы только в случае линейной связи y от х. При нелинейных связях y от х для формулировки остальных выводов нужно анализировать только поле корреляции. Совместный анализ ryx и поля корреляции необходим в случае, когда ryx= 0 (ryx является "незначимым"). Нулевое значение ryx доказывает отсутствие только линейной связи между y и х, но ни в коем случае не опровергает влияния х на y.

Более сложные случаи корреляционного анализа возникают при влиянии на случайную величину (y) нескольких случайных величин (х1, х2, ...xj). В такой ситуации анализируют выборочные коэффициенты частной и множественной корреляции. Анализ частных и множественных коэффициентов корреляции позволяет разобраться в ситуации, когда один из факторов не оказывает непосредственного влияния на y, хотя их парный коэффициент корреляции отличен от нуля.

Более подробно с особенностями проведения корреляционного анализа познакомьтесь самостоятельно.

Таблица 6 - Выводы корреляционного анализа в зависимости от значения ryx

Выводы корреляционного анализа	Значения ryx
1. Наличие связи между y и xj:
есть линейная зависимость между y и x с вероятностью Р	0<
нет линейной зависимости между y и x с вероятностью Р	ryx = 0
есть нелинейная зависимость между y и x (при наличии доказательств в анализе поля корреляции)	ryx = 0
нет зависимости между y и x (при наличии доказательств в анализе поля корреляции)	ryx = 0
2. Характер и тип связи: "функциональная линейная"
"корреляционная линейная"	0<< 1

3. Знак связи: "положительный"	ryx >0
"отрицательный"	ryx <0
4. Теснота (сила) линейной корреляционной связи	Определяется близостью к единице модуля ryx и величиной N по усмотрению исследователя

4. Пример проведения корреляционного анализа

При проведении 8 опытов эксперимента по исследованию влияния содержании полиэтиленовых волокон в бумажном материале (х) на разрушающее материал усилие (y) был получен ряд единичных результатов измерений (табл. 7).

Таблица 7

Результаты эксперимента

Параметры	Значения параметров при уровнях фактора х
эксперимента	№ 1	№ 2	№ 3	№ 4
x, отн. %	100	110	120	130
y1, Н	24	45	52	65
y2, Н	16	35	48	55

Корреляционный анализ полученных результатов измерений решено провести двумя методами: анализом поля корреляции и выборочного коэффициента парной корреляции.

4.1. Анализ поля корреляции

При использовании этого метода выполняем две операции:

1. Строим поле корреляции (рис. 4).

2. Проводим анализ построенного поля корреляции.

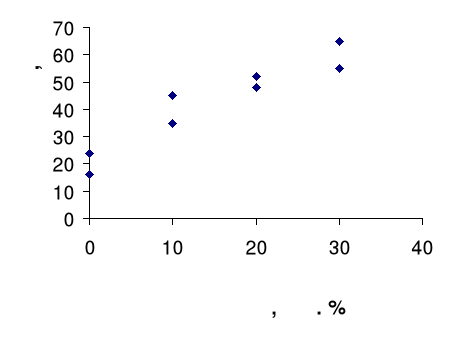
Рис. 4. Поле корреляции

Анализ поля корреляции (рис. 4) позволяет сделать следующие предварительные выводы:

1. Есть зависимость прочности материала от содержания в нем полиэтиленовых волокон.

2. Данная зависимость является корреляционной параболической.

3. Знак зависимости - положительный.

4. Зависимость является тесной.

4.2. Анализ выборочного парного коэффициента корреляции

При использовании данного метода выполняем следующие операции:

Рассчитываем выборочный парный коэффициент линейной корреляции ryx.

2. Проверяем нуль-гипотезу для рассчитанного значения ryx.

3. Анализируем окончательное значение ryx.

Для выполнения расчета ryx первоначально рассчитываем следующие величины:

отн. % ;

Н ;

Sx = 11,95229 12 отн. % ( в результате расчета оставлены две значащие цифры в соответствии с точностью математических вычислений (см. [6]);

Sy = 16,43168 16 Н.

Тогда значение ryx будет равно:

ryx = 0,945611 0,94.

Для проверки нуль-гипотезы рассчитанного значения ryx воспользуемся следующим методом. Согласно этому методу рассчитаем значение квантиля распределения Стьюдента (tр) по формуле

Выберем табличное значение квантиля распределения Стьюдента (tт), приняв вероятность Р = 0,95 и вычислив число степеней свободы f

(f =N-2=8-2= 6). Сравним tт и tр:

tт < tр (2,45 < 6,7).

Из этого неравенства следует, что с вероятностью Р = 0,95 нуль-гипотеза не выполняется, т.е. необходимо считать, что ryx 0 (т.е.
ryx = 0,94).

Анализ выборочного коэффициента линейной корреляции позволяет сделать следующие предварительные выводы:

1. Есть линейная зависимость прочности материала от содержания в нем полиэтиленовых волокон, т.е. введение в материал полиэтиленовых волокон с вероятностью 0,95 оказывает влияние на разрушающего его усилие.

2. Данная зависимость является корреляционной.

3. Знак зависимости - положительный.

4. Зависимость является тесной.

4.3. Окончательные выводы корреляционного анализа

Совместный анализ поля корреляции и окончательного значения выборочного коэффициента парной линейной корреляции (ryx = 0,94) позволяет сделать следующие выводы:

1. Есть зависимость прочности материала от содержания в нем полиэтиленовых волокон, т.е. введение в материал полиэтиленовых волокон с вероятностью 0,95 оказывает влияние на разрушающего его усилие.

2. Данная зависимость с вероятностью 0,95 является корреляционной линейной.

3. Знак зависимости - положительный.

4. Зависимость является тесной.

4.5. Составление планов эксперимента с учетом возможности
проведения корреляционного анализа

Корреляционный анализ не накладывает повышенных требований к планированию эксперимента. Единственным обязательным условием является выполнение соотношения mj 3. Из рекомендаций по планированию эксперимента для проведения корреляционного анализа можно привести следующие. Желательно, чтобы план эксперимента предусматривал:

1) широкую область изменения значений факторов xj;

2) большое число mj значений (уровней) факторов xj, при этом разница между уровнями должна быть больше абсолютной погрешности их измерения;

3) повторные опыты для каждого значения (уровня) факторов xj;

4) большое общее число измерений (N).

PAGE 23

ПЛАНИРОВАНИЕ И АНАЛИЗ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА