Аналоговая и дискретная информация. Носители данных. Операции с данными. Кодирование данных. Системы счисления. Энтропия и количество информации

Лекция 2. Аналоговая и дискретная информация. Носители данных. Операции с данными. Кодирование данных. Системы счисления. Энтропия и количество информации

Аналоговая и дискретная информация. Носители данных

Итак, зарегистрированные сигналы или данные – это результат какого-либо информационного процесса.

Зарегистрированные сигналы могут быть как аналоговыми (регистрируемыми непрерывно и записываемыми в виде графиков), так и дискретными (регистрируемыми через определенные промежутки времени и записываемыми в виде символьного кода: цифрового или буквенного).

Они могут храниться и транспортироваться носителями различных типов (от глиняных дощечек до лазерных дисков). Самый распространенный из носителей, но неэкономичный – это бумага.

Задача преобразования данных при смене носителя - одна из важнейших задач информатики (например: бумажный – оперативная память; оперативная память – жесткий диск; оперативная память – экран монитора и т. п.).

Операции с данными

В ходе информационного процесса над данными производятся разнообразные операции, такие как сбор, формализация, фильтрация, сортировка, группировка, архивация, шифрование, преобразование, транспортировка и другие, что определяется спецификой данных.

Вывод: работа с информацией имеет огромную трудоемкость, и ее необходимо автоматизировать.

Кодирование данных. Системы счисления

Кодирование данных используется издавна: код Морзе, Брайля, морской сигнальный, алфавит и т. п.

В истории человечества для кодировании чисел наиболее известны две системы счисления: непозиционная и позиционная.

Как та, так и другая системы счисления характеризуются основанием – количеством различных цифр, используемых для записи чисел, например, от 0 до 9 (т. е. 10 цифр) в десятичной системе, или I, V, X, L, C, D, M (т. е. 7 цифр) в римской системе счисления.

В непозиционных системах счисления, в частности, римской системе, значение цифры остаётся постоянным, т. е. не зависит от её положения.

Например, используя число 10, обозначаемого как "X" и числа 50, обозначаемого как "L" можно записать число 80 как "LXXX". Очевидно, что для цифры "Х" в любом положении вес одинаков, т. е. равен 10. Точно также, например, число 200 обозначается, как "CC", где каждая цифра "С" соответствует значению 100, независимо от её положения.

В позиционных же системах счисления вес цифры в записи числа, зависит от её положения в числе (позиции или разряда).

Десятичная система счисления, которая применяется в повседневной практике, использует для записи чисел десять арабских цифр (от 0 до 9) – десять пальцев руки.

Существовала пятеричная система расчёта (счёт на пальцах одной руки) и т. п.

Для любой позиционной системы счисления справедливо следующее правило формирования числа на основании входящих в эту систему цифр:

,

или, если расписать сумму в этом выражении,

,

где y – число;

k – основание системы счисления;

xi – цифры числа;

i – номер позиции (разряда) числа, начиная с 0.

Как показала практика, для представления любого числа вполне достаточно системы счисления, состоящей всего из двух символов, что с успехом применяется при работе электронных устройств.

Сохранение любой информации может обеспечиваться использованием двух состояний: наличие – отсутствие. Ячейка памяти, которая, в зависимости от внешнего воздействия, способна принимать одно из двух состояний, обладает минимальной информационной ёмкостью, а её состояния условно обозначаются как "0" и "1".

В компьютерах для кодирования информации в качестве основного кода применяется двоичный или бинарный, представленный позиционной последовательностью нулей и единиц.

Каждый разряд кода ("0" или "1") составляет 1 бит (bit - сокращение от англ. binary digit - двоичное число), т. е. запоминаются два состояния ячейки памяти.

Информация любого типа: символьная, графическая, звуковая кодируется для сохранения на электронных носителях на основании алфавита, состоящего только из двух символов (0, 1), т. е. на основании двоичного кода или двоичной системы счисления.

Информация, представленная в аналоговом виде, для того, чтобы быть сохраненной в электронной памяти, приводится к двоичному коду, т. е. оцифровывается.

В соответствии с тем, что двоичный код имеет позиционную структуру, т. е. старший разряд левее младшего, можно закодировать:

• двумя битами - 4 значения: 00, 01, 10, 11 или (22);
• тремя – 8 значений: 000, 001, 010, 011, 100, 101, 110, 111 или (23);
• четырьмя – 16 значений или 24;
• пятью – 32 значения или 25;
• восемью – 256 значений или (28) и т. п.

Таким образом, общая формула записи двоичного числа:

N=2m,

где m – число разрядов.

Восьмиразрядное двоичное число (28) называют байтом (1 byte = 8 bit).

Биты в байте в последовательности нумеруются слева направо: от 0-го до 7-го.

Минимальная комбинация в одном байте – восемь нулей:

000000002=0*27+0*26+0*25+0*24+0*23+0*22+0*21+0*20 =010

Максимальная – восемь единиц, что соответствует числу 255 в десятичной системе:

111111112=1*27+1*26+1*25+1*24+1*23+1*22+1*21+1*20=128+64+32+16+8+4+2+1=25510

(Подстрочным индексом обозначается основание системы счисления).

Обратное преобразование десятичного кода в двоичный осуществляется делением десятичного числа на 2 до тех пор, пока частное не будет равно единице. Совокупность остатков от деления, записанная слева направо, образует двоичный аналог десятичного числа.

Пример: 13 : 2 = 6 + 1

6 : 2 = 3 + 0

3 : 2 = 1 + 1

1 : 2 = 0 + 1

В итоге: 1310 = 11012 = 23+1*22+0*21+1*20 =1310

Кроме двоичного кода, в информатике используется восьмеричный код и широко применяется шестнадцатеричный код, обозначаемый буквой h (hexadecimal). Этим кодом записывается четырехразрядное двоичное число.

Разряд (24) шестнадцатеричного кода соответствует 16 различным значениям бинарного кода.

Значения от 0 до 9 разряда числа записываются цифрами десятичного кода:

0000 – 0; 0001 – 1; 0010 – 2; 0011 – 3; … 1000 – 8; 1001 – 9;

а остальные значения разряда (в десятичной системе – это уже следующий разряд) записываются первыми буквами латинского алфавита:

1010 – А (10); 1011 – B (11); 1100 – C (12);

1101 – D (13); 1110 – E (14); 1111 – F (15).

Преобразование из шестнадцатеричной системы в десятичную осуществляется просто, например:

A3h = 1010 00112 = 10*161 + 3*160 =16310

Проверка:. 1*27+1*25+1*21+1*20 = 128 + 32 + 2 + 1 = 160 + 3 = 16310

Другой пример: FAh = 1111 10102 = 15*161+10*160 = 25010

Проверка: 27+26+25+24+23+21 = 128+64+32+16+8+2 = 25010

Ещё пример перевода шестнадцатеричного числа 30ЕD16 в десятичное:

30ЕD16 = 3*163 + E*161 + D*160 = 3*4096 + 14*16 + 13 = 1252510

Преобразование из десятичной в шестнадцатеричную осуществляется (аналогично двоичной) делением на основание (16) и с записью остатка слева направо:

250 : 16 = 15 +10 (младший разряд - 160 * А);

15 : 16 = 0 +15 (старший разряд - 161 * F).

Итог: FAh = 15*161+10*160=25010

Правило 1.

Перевод целого десятичного числа в систему счисления с любым основанием осуществляется делением его на основание системы счисления.

Для перевода правильной дроби какой-либо системы счисления в дробь десятичной системы нужно представить дробные разряды исходной системы в виде простых дробей со знаменателями, соответствующими степеням числа, найти наименьший общий знаменатель и рассчитать десятичную дробь.

Пример: 0,CAh = 12/161 + 10/162 = 192/256 + 10/256 = 202/256=0,78910

При переводе правильной десятичной дроби в любую другую систему счисления её нужно последовательно умножать на основание заданной системы счисления. В каждом шаге умножения участвуют только дробные части. Процесс умножения продолжается до получения требуемого числа знаков (если точный перевод не возможен) или произведения, дробная часть которого равна нулю.

Целые числа произведения, начиная с первого, являются значениями разрядов правильной дроби в заданной системе. (При округлении величина погрешности равна половине веса цифры заданной системы счисления).

Пример перевода правильной дроби 0,655110 в восьмеричную систему:

0,6551*8 = 5,2408 5

0,2408*8 = 1,9264 1

0,9264*8 = 7,4112 7

0,4112*8 = 3,2896 3

В результате: 0,655110 = 0,51738

Правило 2.

Перевод правильной десятичной дроби в систему счисления с любым основанием осуществляется умножением на основание системы счисления, считыванием целой части полученных произведений сверху вниз и записью их слева направо.

Энтропия и количество информации

Получение любой информации сопровождается снятием какой-то неопределенности.

Задача, которая решается в ходе снятия неопределенности – это уменьшение количества рассматриваемых вариантов и выбор соответствующего ситуации варианта из числа всех возможных. Снятие неопределенности дает возможность принимать обоснованные управляющие решения и действовать.

Например, покупатель в магазине просит продать жевательную резинку. Продавец, у которого 16 сортов жевательной резинки, затрудняется в том, что предложить.

Но если уточнить: "Orbit", сортов которой половина, то теперь из 16 первоначальных вариантов продавец будет рассматривать только 8 вариантов, соответствующих марке "Orbit", т. е. неопределенность уменьшилась в два раза, и это соответствует получению 1 бита информации.

Если же покупатель сразу указывает пальцем на витрину: "Вот эту!", то неопределенность снимается полностью. Этим жестом (1 из 16 вариантов) продавцу сообщается уже 4 бита информации.

Максимальная неопределенность возникает при наличии нескольких равновероятных вариантов.

Минимальная неопределенность будет равна нулю, когда выбор одного из вариантов сделан, т. е. – это ситуация полной определенности, означающая то, что вся необходимая информация получена.

Величина, характеризующая количество неопределенности в теории информации обозначается символом H и имеет название энтропия, или информационная энтропия.

Энтропия (H) – мера неопределенности, выраженная в битах. Энтропию можно так же рассматривать как меру равномерности распределения (рассеяния) случайной величины.

При полном рассеянии (равномерном распределении) энтропия максимальна, а при полной упорядоченности отсутствует. Примером максимальной величины энтропии (максимального рассеяния) может служить "белый шум" в радиоэфире.

Поведение энтропии для случая двух альтернатив

На рисунке показано поведение энтропии для случая двух вероятных событий, при изменении соотношения их вероятностей

(p, (1-p)).

Максимального значения энтропия достигает тогда, когда обе вероятности равны между собой, т. е. равны , а нулевое значение энтропии соответствует случаям (p0=0, p1=1) и (p0=1, p1=0).

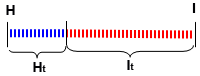
Рис. Связь между энтропией и количеством информации.

Соотношение энтропии (H) и количества информации (I), характеризующих одну и ту же ситуацию представлено на рисунке. Можно сказать, что I – это количество информации, которое требуется для снятия неопределенности H, или, другими словами, что информация –это отрицательная энтропия.

Когда неопределенность снята полностью, количество полученной информации I равно изначально существовавшей неопределенности H.

При частичном снятии неопределенности, полученное количество информации и оставшаяся неснятой неопределенность составляют в сумме исходную неопределенность: Ht + It = H.

Исходя из этого, формулы, по которым рассчитывается энтропия H, являются и формулами для расчета количества информации I, т. е. когда речь идет о полном снятии неопределенности, в них H можно заменить на I.

PAGE \* MERGEFORMAT6

EMBED Excel.Chart.8 \s

Аналоговая и дискретная информация. Носители данных. Операции с данными. Кодирование данных. Системы счисления. Энтропия и количество информации