Электронно-дырочный переход. Электронно-дырочный переход в состоянии равновесия
PAGE 1
Лк 3-4
Электронно-дырочный переход
Электронно-дырочный переход в состоянии равновесия
Принцип действия большинства полупроводниковых приборов основан на физических явлениях, происходящих в области контакта твердых тел. При этом преимущественно используются контакты: полупроводник-полупроводник; металл-полупроводник; металл-диэлектрик-полупроводник.
Если переход создается между полупроводниками n-типа и p-типа, то его называют электронно-дырочным или p-n переходом.
Электронно-дырочный переход создается в одном кристалле полупроводника с использованием сложных и разнообразных технологических операций.
Рассмотрим p-n переход, в котором концентрации доноров Nд и акцепторов Na изменяются скачком на границе раздела (рис. 1.7, а). Такой p-n переход называют резким. Равновесная концентрация дырок в p-области () значительно превышает их концентрацию в n-области (). Аналогично для электронов выполняется условие > . Неравномерное распределение концентраций одноименных носителей зарядов в кристалле (рис. 1.7, б) приводит к возникновению диффузии электронов из n-области в p-область и дырок из p-области в n-область. Такое движение зарядов создает диффузионный ток электронов и дырок. С учетом выражений (1.13) и (1.14) плотность полного диффузионного тока, проходящего через границу раздела, определится суммой
.
Электроны и дырки, переходя через контакт навстречу друг другу (благо- даря диффузии), рекомбинируют и в приконтактной области дырочного полу- проводника образуется нескомпенсированный заряд отрицательных ионов акцепторных примесей, а в электронном полупроводнике нескомпенсирован -ный заряд положительных донорных ионов (рис. 1.6, в). Таким образом, электронный полупроводник заряжается положительно, а дырочный - отрицательно. Между областями с различными типами электропроводности возникает собственное электрическое поле напряженностью Eсоб (рис. 1.7, а), созданное двумя слоями объемных зарядов.
Этому полю соответствует разность потенциалов Uк между n- и p-областями, называемая контактной (рис. 1.7, г). За пределами области объемного заряда полупроводниковые области n- и р-типа остаются электрически нейтральными.
Собственное электрическое поле является тормозящим для основных носителей заряда и ускоряющим для неосновных. Электроны p-области и 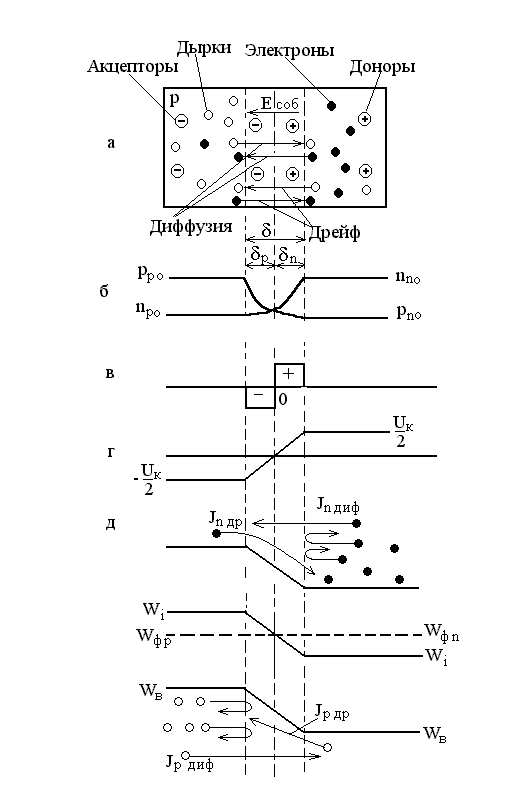
Рисунок 1.7 Равновесное состояние p-n перехода.
дырки n-области, совершая тепловое движение, попадают в пределы диффузионного электрического поля, увлекаются им и перебрасываются в противоположные области, образуя ток дрейфа, или ток проводимости.
Выведение носителей заряда из области полупроводника, где они являются неосновными, через электронно-дырочный переход ускоряющим электрическим полем называют экстракцией носителей заряда.
Используя выражение (1.12) и учитывая, что Е = -dU/dx, определяем плотность полного дрейфового тока через границу раздела p- и n-областей:
.
Так как через изолированный полупроводник ток проходить не должен, между диффузионным и дрейфовым токами устанавливается динамическое равновесие:
. (1.15)
Приконтактную область, где имеется собственное электрическое поле, называют p-n переходом.
Поскольку потенциальная энергия электрона и потенциал связаны соотношением W = -qU, образование нескомпенсированных объемных зарядов вызывает понижение энергетических уровней n-области и повышение энергетических уровней р-области. Смещение энергетических диаграмм прекратится, когда уровни Ферми W фn и W фp совпадут (рис. 1.7, д). При этом на границе раздела (x = 0) уровень Ферми проходит через середину запрещенной зоны. Это означает, что в плоскости сечения x = 0 полупроводник характеризуется собственной электропроводностью и обладает по сравнению с остальным объемом повышенным сопротивлением. В связи с этим его называют запирающим слоем или областью объемного заряда.
Совпадение уровней Ферми n- и p-областей соответствует установлению динамического равновесия между областями и возникновению между ними потенциального барьера Uk для диффузионного перемещения через p-n переход электронов n-области и дырок p-области.
Из рис. 1.7, д следует, что потенциальный барьер
.
Подстановка в это выражение результатов логарифмирования соотношений (1.4), (1.7) позволяет получить следующее равенство:
.
Если обозначить т = kT/q и учесть уравнение (1.10), то можно записать:
; (1.16) . (1.17)
Из уравнений (1.16) и (1.17) следует:
; . (1.18)
При комнатной температуре (Т = 300 К) т 0,026 В.
Таким образом, контактная разность потенциалов зависит от отношения концентраций носителей зарядов одного знака в р- и n-областях полупроводника.
Другим важным параметром p-n перехода является его ширина, обозначаемая = p + n.
Ширину запирающего слоя можно найти, решив уравнения Пуассона для n-области и p-области:
; (1.19) . (1.20)
Решения уравнений (1.19) и (1.20) при граничных условиях
; ;
имеют вид:
для -p < x < 0;
для 0 < x <n; (1.21)
В точке x = 0 оба решения должны давать одинаковые значения и . Приравняв и , можно записать:
. (1.22)
Из равенства (1.22) видно, что ширина слоев объемных зарядов в n- и p-областях обратно пропорциональна концентрациям примесей и в несимметричном переходе запирающий слой расширяется в область с меньшей концентрацией примесей.
На основании равенства (1.22) можно записать:
; , (1.23)
где = n + р.
Приравнивая правые части уравнений (1.21) и учитывая соотношения (1.23), при x = 0 получаем
.
На основании этого выражения формулу для определения ширины запирающего слоя p-n перехода можно записать в следующем виде:
. (1.24)
Из соотношения (1.24) видно, что на ширину запирающего слоя существенное влияние оказывает концентрация примесных атомов. Увеличение концентрации примесных атомов сужает запирающий слой, а уменьшение расширяет его. Это часто используется для придания полупроводниковым приборам требуемых свойств.
Прямое включение p-n перехода
При использовании p-n перехода в полупроводниковых приборах к нему подключается внешнее напряжение. Величина и полярность этого внешнего напряжения определяют электрический ток, проходящий через p-n переход.
Если положительный полюс источника питания подключается к
р-области, а отрицательный полюс - к n-области, то включение p-n перехода называют прямым. При изменении указанной полярности источника питания включение p-n перехода называют обратным.
Прямое включение p-n перехода показано на рис. 1.8. Поскольку сопротивление p-n перехода значительно превышает сопротивление нейтральных p- и n-областей, внешнее напряжение Uпр почти полностью падает на этом переходе.
Прямое напряжение создает в переходе внешнее электрическое поле, направленное навстречу собственному.
Напряженность результирующего поля падает, и уровни Ферми смещаются таким образом, что потенциальный барьер уменьшается до Uк - Uпр. Это сопровождается сужением запирающего слоя, ширина которого может быть найдена из соотношения (1.24) подстановкой вместо Uк величины Uк - Uпр:
.
В результате снижения потенциального барьера большее количество основных носителей зарядов получает возможность диффузионно переходить в соседнюю область, что сопровождается ростом тока диффузии. Ток дрейфа при этом не изменится, поскольку он зависит от количества неосновных носителей, появляющихся на границах p-n перехода. Это количество зависит только от концентрации примесей в полупроводнике и температуры.
Увеличение диффузионной составляющей тока через p-n переход при неизменной дрейфовой составляющей приводит к нарушению термодинамического равновесия, устанавливаемого выражением (1.15). Через переход будет проходить результирующий ток, определяемый диффузионной составляющей.
Дополнительная диффузия носителей зарядов приводит к тому, что на границе p-n перехода повышаются концентрации дырок в области n-типа до некоторого значения и электронов в p-области до значения . Повышение концентраций неосновных носителей в p- и n-областях вследствие влияния внешнего напряжения, приложенного к электронно-дырочному переходу,
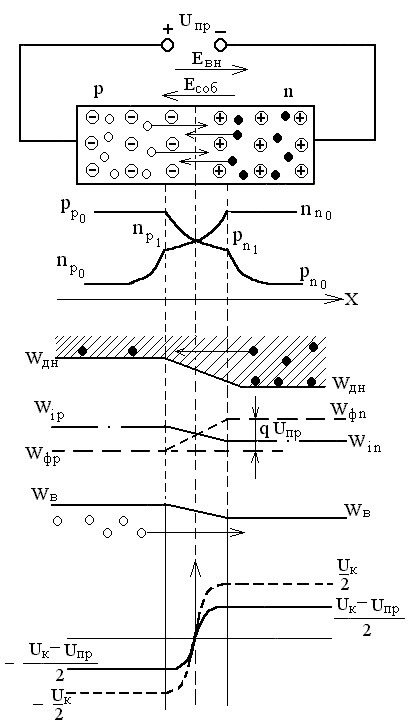
Рисунок 1.8 Прямое включение p-n перехода.
получило название инжекции неосновных носителей. Область, из которой происходит инжекция, называют эмиттером, а область, в которую осуществляется инжекция, — базой.
Поскольку при прямом включении p-n перехода потенциальный барьер уменьшается, концентрации неосновных носителей на границах p-n перехода могут быть рассчитаны по формулам (1.18) при замене Uк величиной Uк - Uпр. Тогда:
; (1.25)
. (1.26)
Из выражений (1.25) и (1.26) следует, что на границах p-n перехода под действием прямого напряжения Uпр происходит увеличение концентраций неосновных носителей.
Неравновесные неосновные носители зарядов диффундируют в глубь полупроводника и нарушают его электронейтральность. Восстановление нейтрального состояния полупроводников происходит за счет поступления носителей зарядов от внешнего источника. Это является причиной возникновения тока во внешней цепи, называемого прямым и обозначаемого Iпр.
Концентрации неосновных носителей в нейтральной области полупроводника зависят от координаты x. Закон их распределения может быть найден путем решения уравнения непрерывности для установившегося состояния, т. е. состояния, при котором концентрация неосновных носителей не изменяется во времени. Этому условию соответствуют уравнения непрерывности, которые при Е = 0 записываются в следующем виде:
; (1.27) ; (1.28)
где - диффузионная длина дырок в n-области; - диффузионная длина электронов в p-области.
Решения уравнений непрерывности (1.27) и (1.28) для нейтральной области полупроводников (начало отсчета координаты совпадает с границами p-n перехода) при очевидных из рис. 1.7 начальных условиях и с учетом соотношений (1.25) и (1.26) имеют вид:
; (1.29)
. (1.30)
Таким образом, на границе запирающего слоя (x = 0) за счет инжекции концентрация носителей повышается и достигает следующих значений:
; .
Уравнения (1.29) и (1.30) показывают, что в неравновесном состоянии при удалении от p-n перехода концентрации неосновных носителей зарядов вследствие рекомбинации убывают по экспоненциальному закону от значений и до и .
При x = Lp и x = Ln концентрации неосновных носителей уменьшаются в 2,7 раза. Таким образом, диффузионная длина - это расстояние, на котором концентрация неосновных носителей в неравновесном состоянии уменьшается в е раз.
Обратное включение р-п-перехода
При включении p-n перехода в обратном направлении (рис. 1.9) внешнее обратное напряжение Uобр создает электрическое поле, совпадающее по направлению с собственным, что приводит к росту потенциального барьера на
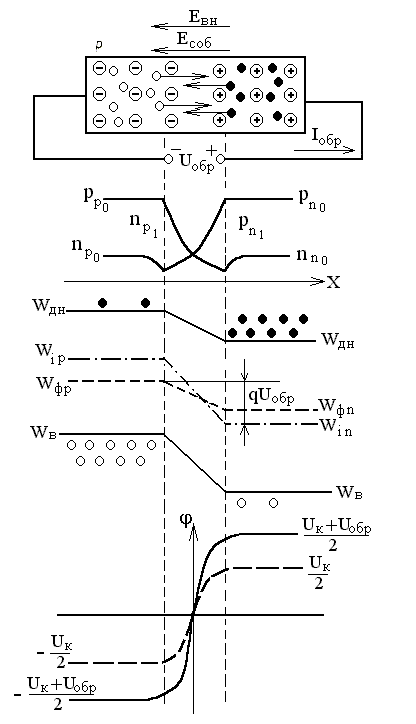
Рисунок 1.9 Обратное включение p-n перехода.
величину Uобр и увеличению относительного смещения энергетических диаграмм на q(Uk + Uобр). Это сопровождается увеличением ширины запирающего слоя, которая может быть найдена из соотношения (1.24) подстановкой вместо Uk величины Uk + Uобр.
. (1.31)
Возрастание потенциального барьера уменьшает диффузионные токи основных носителей (т. е. меньшее их количество преодолеет возросший потенциальный барьер). Для неосновных носителей поле в p-n переходе остается ускоряющим, и поэтому дрейфовый ток, как было показано в п. 1.3.2, не изменится.
Уменьшение диффузионного тока приведет к нарушению условия равновесия, устанавливаемого выражением (1.15). Через переход будет проходить результирующий ток, определяемый в основном током дрейфа неосновных носителей.
Концентрация неосновных носителей у границ p-n перехода вследствие уменьшения диффузионного перемещения основных носителей уменьшится до некоторых значений и . По мере удаления от p-n перехода концентрация неосновных носителей будет возрастать до равновесной. Значение концентрации неосновных носителей заряда на любом удалении x от границ p-n перехода можно рассчитать по следующим формулам, полученным при решении уравнения непрерывности для обратного, включения p-n перехода:
; (1.32)
. (1.33)
Теоретическая вольтамперная характеристика p-n перехода
Вольтамперная характеристика представляет собой график зависимости тока во внешней цепи p-n перехода от значения и полярности напряжения, прикладываемого к нему. Эта зависимость может быть получена экспериментально или рассчитана на основании уравнения вольтамперной характеристики.
При включении p-n перехода в прямом направлении в результате инжекции возникает прямой диффузионный ток.
Уравнения для плотности электронной и дырочной составляющих прямого тока получаются подстановкой соотношений (1.29) и (1.30) в (1.13) и (1.14) и, записываются в следующем виде:
; .
Плотность прямого тока, проходящего через p-n переход, можно определить как сумму jпр = jn диф + jp диф, не изменяющуюся при изменении координаты х. Если считать, что в запирающем слое отсутствуют генерация и рекомбинация носителей зарядов, то плотность прямого тока, определяемая на границах p-n перехода (при x = 0),
. (1.34)
Включение p-n перехода в обратном направлении приводит к обеднению приконтактной области неосновными носителями и появлению градиента их концентрации. Градиент концентрации является причиной возникновения диффузионного тока неосновных носителей.
На основании соотношений (1.13), (1.14) и (1.32), (1.33) выражение для расчета плотности обратного тока может быть записано в виде
. (1.35)
Объединяя выражения (1.34) и (1.35), можно записать уравнение для плотности тока в общем виде:
, (1.36) где .
Величину js называют плотностью тока насыщения. Умножив правую и левую части выражения (1.36) на площадь П p-n перехода, получим уравнение теоретической вольтамперной характеристики:
, (1.37)
где IS- ток насыщения. В это уравнение напряжение U подставляется со знаком "плюс" при включении p-n перехода в прямом направлении и со знаком "минус" при обратном включении.
Уравнение (1.37) позволяет рассчитать теоретическую вольтамперную характеристику тонкого электронно-дырочного перехода, в котором отсутствуют генерация и рекомбинация носителей зарядов.
Теоретическая вольтамперная характеристика p-n перехода, построенная на основании уравнения (1.37), приведена на рис. 1.10. При увеличении
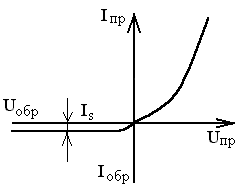
Рисунок 1.10 Теоретическая вольтамперная характеристика p-n перехода.
обратного напряжения ток через p-n переход стремится к предельному значению js, которого достигает при обратном напряжении примерно 0,1...0,2 В.
На основании соотношений (1.2), (1.5), (1.8) и (1.10), считая, что все атомы примесей ионизированы, т. е. = Na, для области рабочих температур можно записать: . (1.38)
Из соотношения (1.38) видно, что чем больше ширина запрещенной зоны полупроводника и концентрация примесей доноров и акцепторов, тем меньше ток насыщения, а с увеличением температуры ток насыщения растет по экспоненциальному закону.
Процессы генерации и рекомбинации носителей в запирающем слое оказывают существенное влияние на вид вольтамперной характеристики. В отсутствие внешнего напряжения между процессами генерации и рекомбинации устанавливается равновесие. При приложении к p-n переходу обратного напряжения дырки и электроны, образующиеся в результате генерации, выводятся полем запирающего слоя. Это приводит к возникновению дополнительного тока генерации Iген, совпадающего с обратным током p-n перехода. Можно показать, что при = , n = р = 0 и Ln = Lp = L0 справедливо соотношение
, (1.39)
где 0 - толщина запирающего слоя.
Из выражения (1.39) видно, что генерационная составляющая обратного тока растет при увеличении ширины запрещенной зоны полупроводника, так как при этом уменьшается значение ni, а также при увеличении концентрации примесей, при которой возрастает . Например, при одинаковых значениях 0 и L0 для германия ni = 2,51013 см-3 (W = 0,67 эВ) и Iген= 0,1Is, а для кремния ni = 6,81010 см-3 (W = 1,12 эВ) и Iген = 3000IS,.
Таким образом, если в германиевых p-n переходах током генерации можно пренебречь, то в кремниевых p-n переходах он является основной составляющей обратного тока. Поэтому на вольтамперных характеристиках кремниевых p-n переходов нет выраженного участка насыщения.
Емкости p-n перехода
Изменение внешнего напряжения dU на p-n переходе приводит к изменению накопленного в нем заряда dQ. По�этому p-n переход ведет себя подобно конденсатору, ем�кость которого С = dQ/ dU.
В зависимости от физической природы изменяющегося заряда различают емкости барьерную (зарядную) и диф�фузионную.
Барьерная (зарядная) емкость определяется измене�нием нескомпенсированного заряда ионов при изменении ширины запирающего слоя под воздействием внешнего обратного напряжения. Поэтому идеальный электронно-дырочный переход можно рассматривать как плоский кон�денсатор, емкость которого определяется соотношением
, (1.41)
где П, - соответственно площадь и толщина p-n перехода.
Из соотношений (1.41) и (1.31) следует
.
В общем случае зависимость зарядной емкости от при�ложенного к p-n переходу обратного напряжения выра�жается формулой
,
где C0 — емкость p-n перехода при UОБР = 0; - коэффици�ент, зависящий от типа p-n перехода (для резких p-n переходов = 1/2, а для плавных = 1/3).
Барьерная емкость увеличивается с ростом NА и NД, а также с уменьшением обратного напряжения. Характер зависимости СБАР = f(UОБР) показан на рис. 1.13,а.
Рассмотрим диффузионную емкость. При увеличении внешнего напряжения, приложенного к p-n переходу в прямом направлении, растет концентрация инжектирован�ных носителей вблизи границ перехода, что приводит к изменению количества заря�да, обусловленного неосновны�ми носителями в p- и n-областях. Это можно рассмат�ривать как проявление неко�торой емкости. Поскольку она зависит от изменения диффузионной составляю�щей тока, ее называют диф�фузионной. Диффузионная емкость представляет собой отношение приращения инжекционного заряда dQинж к вызвавшему его изменению напряжения dUпр, т. е. . Воспользовавшись уравнением (1.30), можно опреде�лить заряд инжектированных носителей, например дырок в n-области:
.
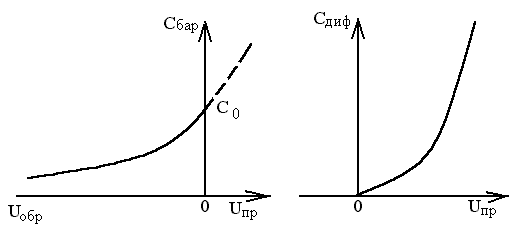
Рисунок 1.13 Зависимость барьерной (а) и диффузионной (б) емкостей p-n перехода от напряжения.
.
Тогда диффузионная емкость, обусловленная изменением общего заряда неравновесных дырок в n-области, опреде�лится по формуле
.
Аналогично для диффузионной емкости, обусловленной инжекцией электронов в p-область,
.
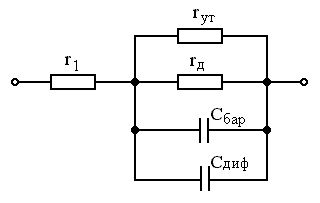
Рисунок 1.13 Эквивалентная схема p-n перехода.
Общая диффузионная емкость
.
Зависимость ёмкости от прямого напряжения на p-n переходе показана на рисунке 1.13, б.
Полная емкость p-n перехода определяется сум�мой зарядной и диффузи�онной емкостей:
.
При включении p-n перехода в прямом направ�лении преобладает диффу�зионная емкость, а при включении в обратном на�правлении - зарядная.
На рис. 1.14 приведена эквивалентная схема p-n перехода по переменному току. Схема содержит дифферен�циальное сопротивление p-n перехода rД, диффузионную емкость СДИФ, барьерную емкость СБАР и сопротивление объ�ема p- и n-областей r1. На основании уравнения (1.37) можно записать:
.
Если при прямом включении p-n перехода Uпр >> т, то:
; .
При комнатной температуре ; (1.42)
(в соотношении (1.42) значение тока подставляется в ам�перах). Сопротивление утечки rУТ учитывает возможность прохождения тока по поверхности кристалла из-за несо�вершенства его структуры. При прямом включении p-n перехода СБАР << СДИФ, дифференциальное сопротивление rД ПР мало и соизмеримо с r1, поэтому эквивалентная схе�ма принимает вид, показанный на рис. 1.15, а.
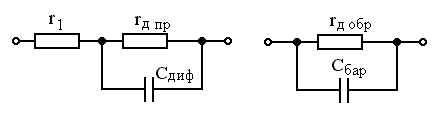
Рисунок 1.15 Упрощенные эквивалентные схемы p-n перехода.
При обратном смещении rД ОБР >> r1, СБАР >> СДИФ и эк�вивалентная схема имеет вид, показанный на рис. 1.15, б.
Электронно-дырочный переход. Электронно-дырочный переход в состоянии равновесия