Размерные цепи

Одним из самых эффективных методов расчета геометрических параметров составных частей конструкций, является метод размерных цепей. Метод позволяет устанавливать расчетом допуски и отклонения геометрических параметров или проверить правильность их назначения для обеспечения собираемости и работоспособности изделий.

Использование методов расчёта размерных цепей позволяют сократить как время так и материальные затраты на этапе технической подготовки и производства конструкций, повысить качество и сократить сроки отработки изделий, их конструкторской и технологической документации. Каждая размерная цепь имеет одно замыкающее звено. Замыкающими такие звенья называют потому, что в процессе сборки изделия или при обработке элементов отдельных деталей они замыкают реальную размерную цепь. Замыкающие звенья размерной цепи непосредственно не выполняются, а являются результатом выполнения (в том числе изготовления) всех других звеньев, составляющих размерную цепь. Применяемые методы достижения точности замыкающего звена, т.е. методы расчёта размерных цепей, показаны на Рисунке 1.

Любая размерная цепь имеет замыкающее звено и составляющие звенья размерной цепи. Из приведённых методов расчёта размерных цепей базовым можно считать «метод полной взаимозаменяемости», на основе которого получены основные определения и зависимости. Рассмотрение других методов после освоения «метода полной взаимозаменяемости» становится менее затруднительным.

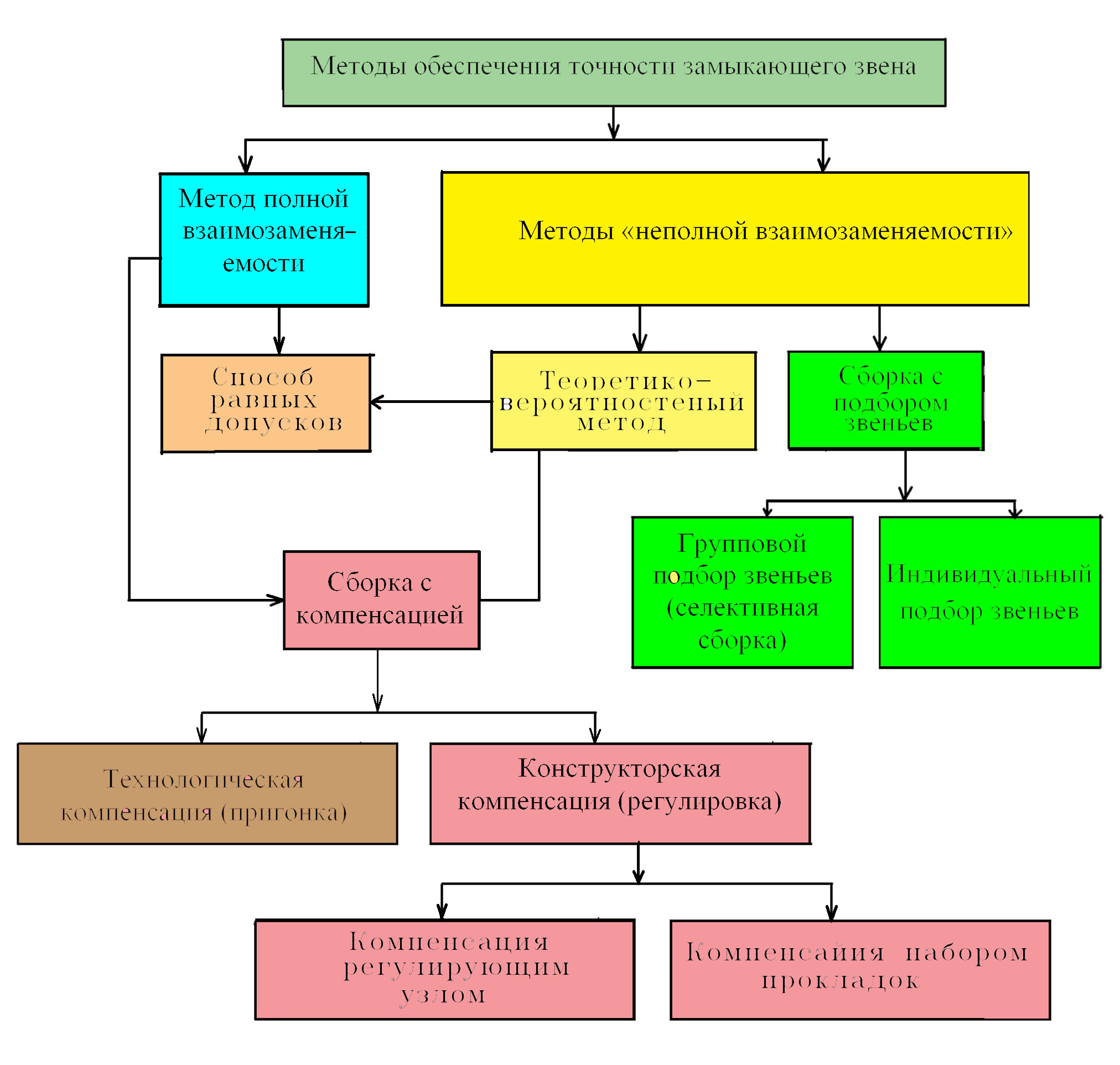
Рисунок 1. Методы обеспечения точности замыкающего звена

Основные определения и классификация размерных цепей

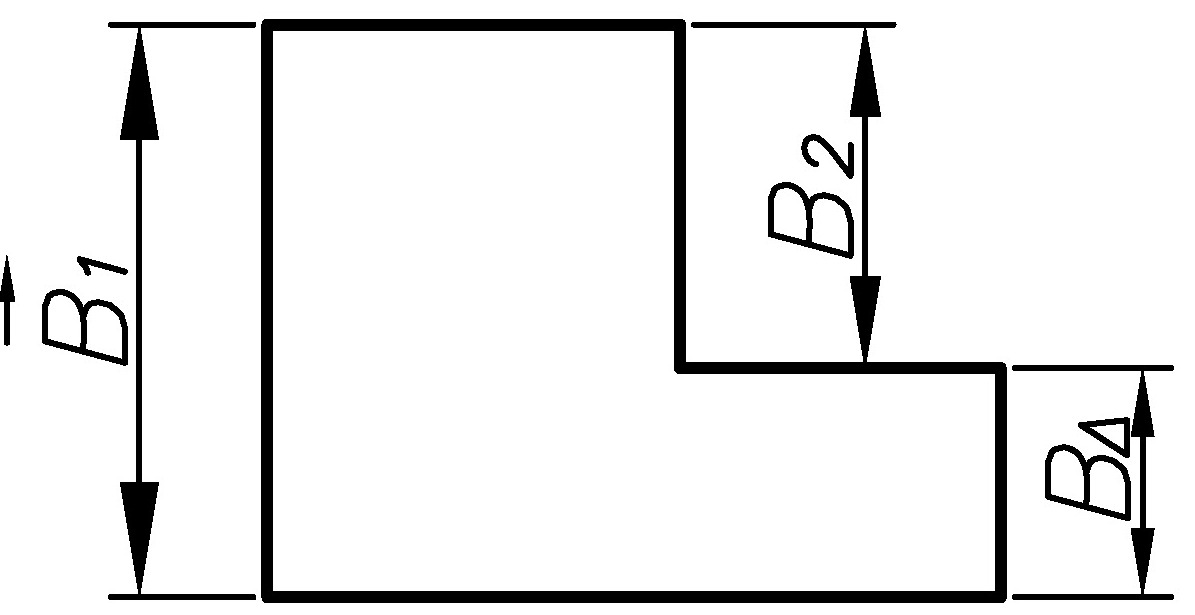
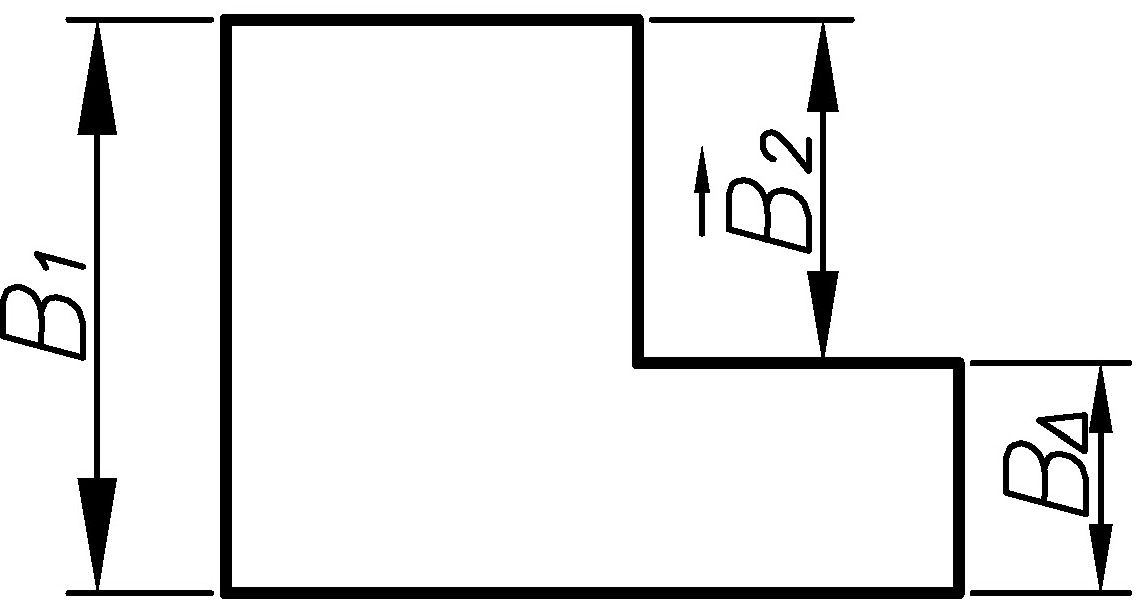
Размерной цепью называется совокупность взаимосвязанных размеров, определяющих взаимное расположение осей и поверхностей одной детали (детальная размерная цепь, рис. 2) или нескольких деталей в изделии (сборочная размерная цепь, рис.3), расположенных в определённой последовательности по замкнутому контуру и непосредственно влияющих на точность одного из размеров контура.

Каждая размерная цепь состоит из составляющих звеньев (размеров) цепи и замыкающего звена (размера). Геометрические схемы позволяют исключить возможность ошибок и упростить задачу выявления размерных цепей, особенно при сложных многозвенных цепях.

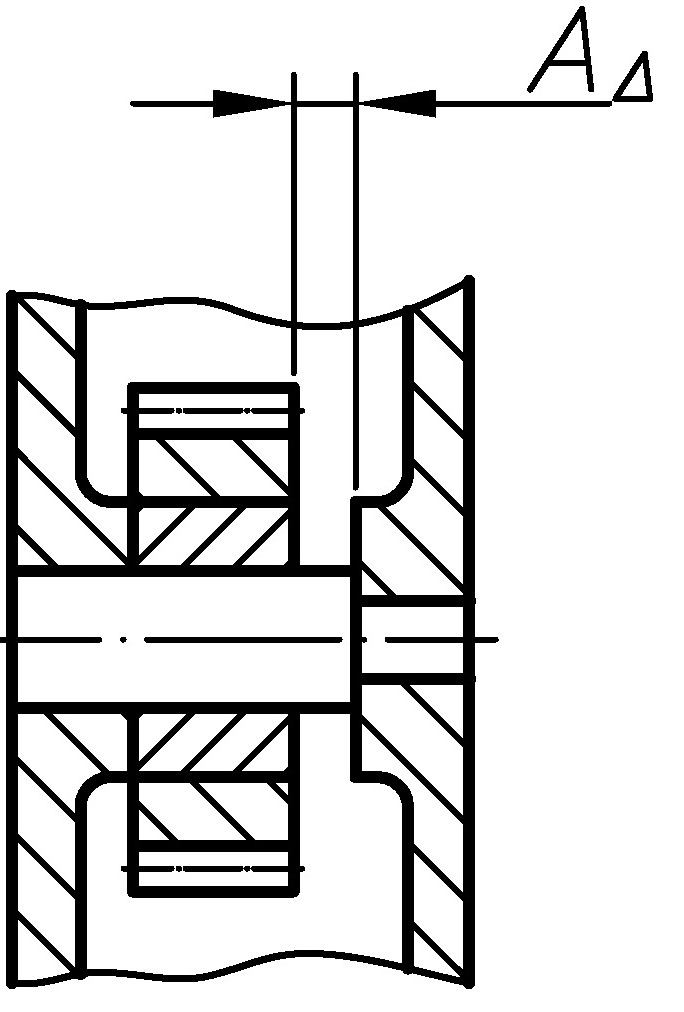
Замыкающим размером (А; рис.2,3,4) называется размер, получающийся последним в процессе обработки детали или сборки узла, величина и точность которого зависят от величины и точности всех остальных размеров цепи, называемых составляющими (А1, A2...An-1; рис. 2, 3).

К числу основных типовых замыкающих звеньев размерных цепей относят:

зазоры и натяги в сопряжениях деталей;
выступы и перекрытия элементов одних деталей относительно других;
симметричность поверхностей;
зацепление поверхностей одних деталей относительно других;
соосность цилиндрических поверхностей одной или нескольких деталей;
расстояния между поверхностями деталей, определяющие начало и конец воздействия одной детали на другую.

Классификация звеньев размерных цепей размерных цепей показана в таблице 1.

По взаимному расположению размеров размерные цепи делятся на линейные, плоскостные и пространственные.

Линейными называются размерные цепи, звенья которых расположены параллельно друг другу (рис. 2, 3)

Плоскостными называются размерные цепи, все или часть звеньев которых не параллельны друг другу, но расположены в одной или нескольких параллельных плоскостях (рис. 4).

Пространственными называются размерные цепи, все или часть звеньев которых не параллельны друг другу и расположены в непараллельных плоскостях.

Угловыми называются размерные цепи, все звенья которых - угловые величины. Признаками составляющих размеров угловой цепи часто бывают отклонения от перпендикулярности, отклонения от параллельности осей и поверхностей и тому подобные погрешности взаимного расположения поверхностей и осей деталей.

Классификация звеньев размерных цепей

Таблица 1

Определение	Примеры
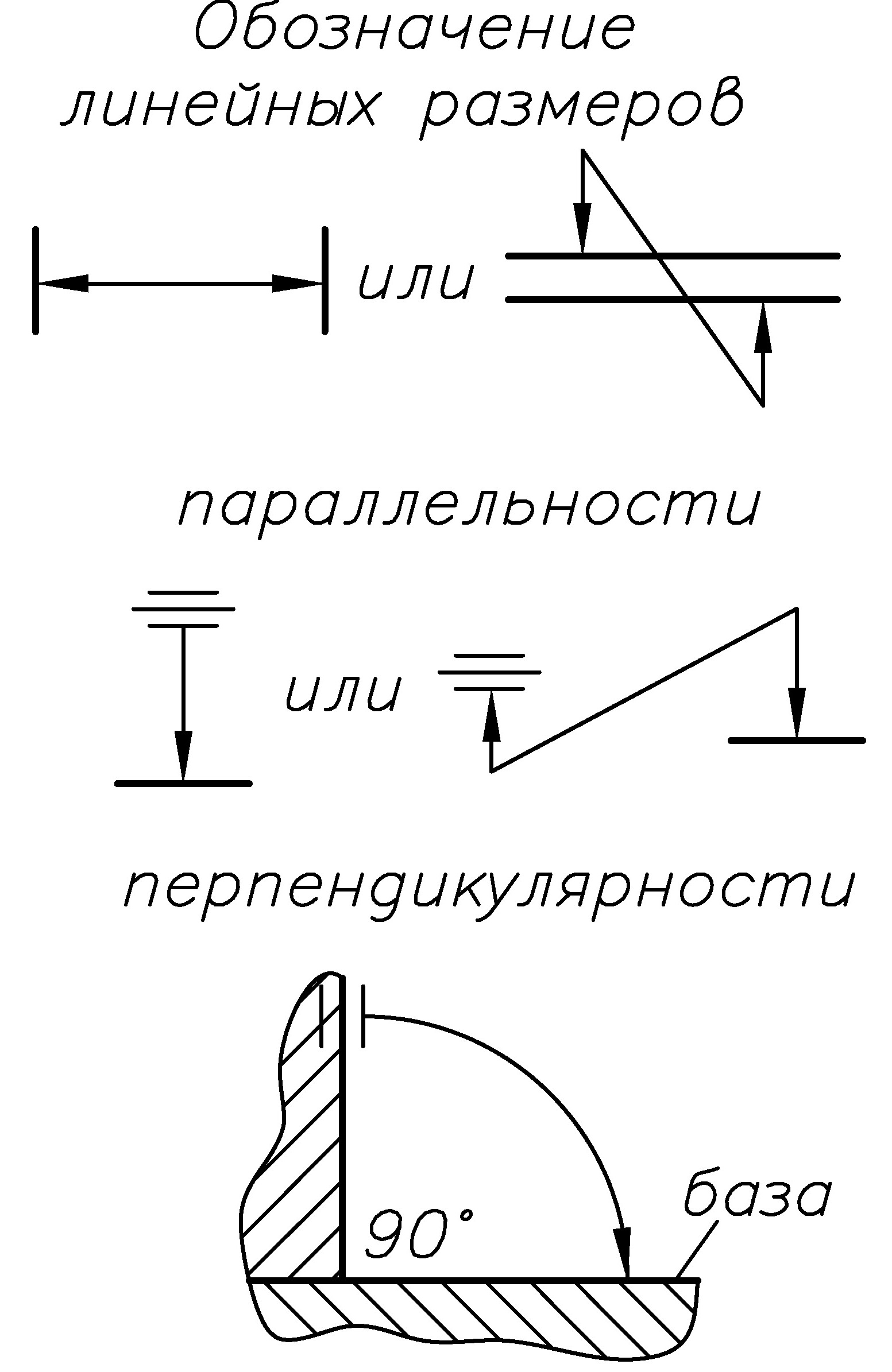
Звено	Один из размеров, образующих размерную цепь. На схемах размерных цепей условно обозначают звенья: линейные размеры – двусторонней стрелкой; параллельность и перпендикулярность – односторонней стрелкой с направлением острия стрелки к базе
Замыкающее	Звено размерной цепи, являющееся исходным при постановке задачи. Например, при конструировании, исходя из служебного назначения механизма, устанавливают технические требования (предельные размеры) к зазору А - замыкающему звену
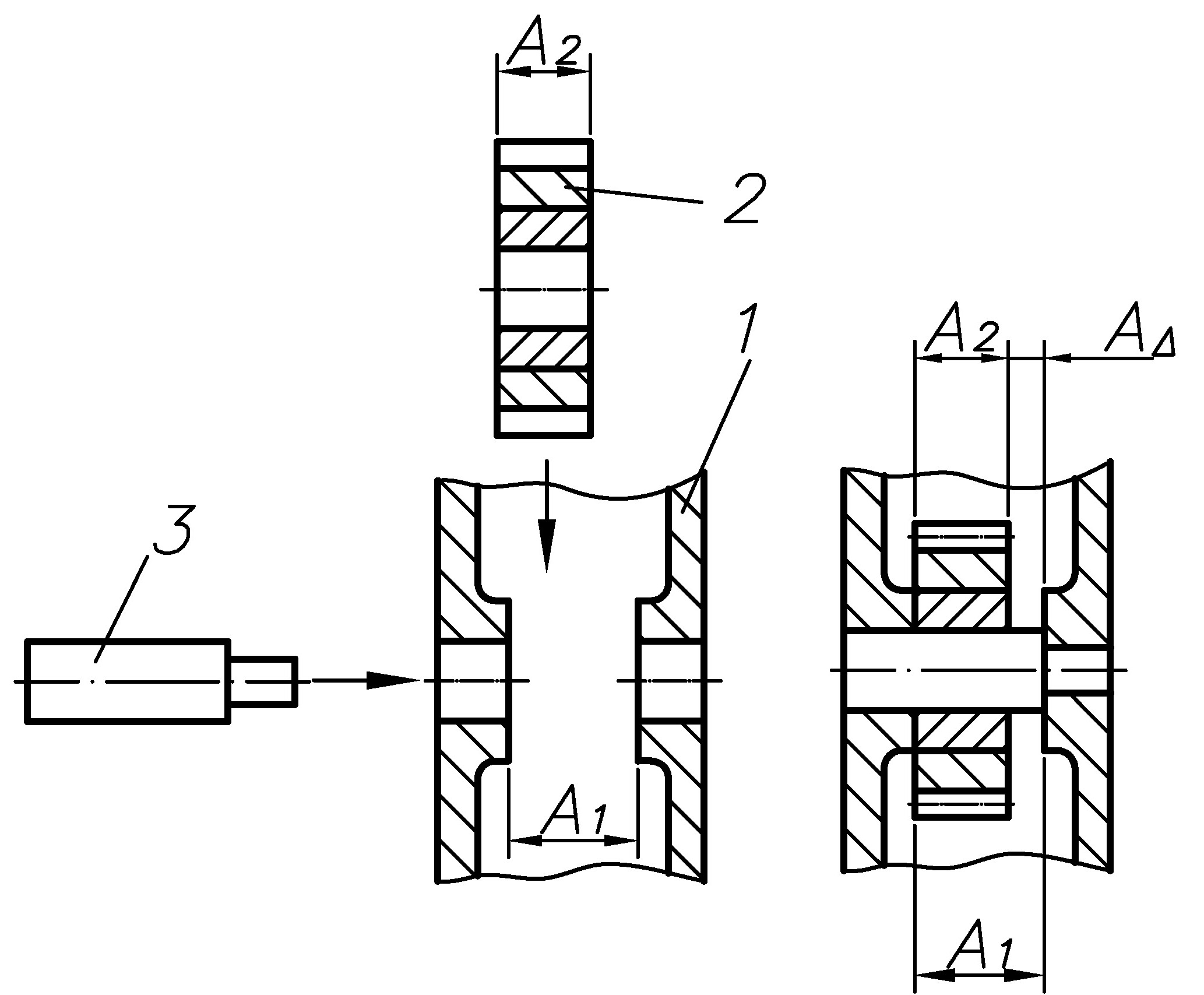
	Звено размерной цепи, получающееся последним в результате решения поставленной задачи. Например, при сборке редуктора в его корпус 1 устанавливают зубчатое колесо 2 и вал 3. Последним звеном размерной цепи является зазор А - замыкающее звено

Продолжение табл. 1

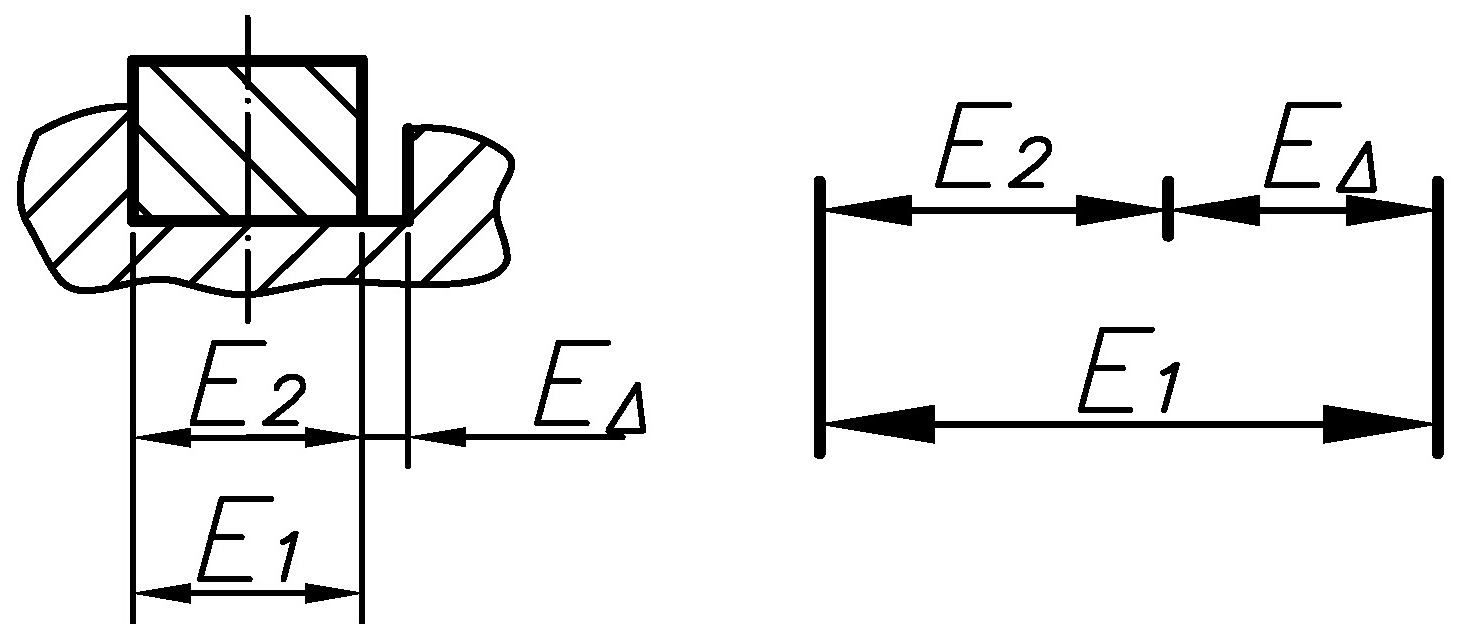
Составляющее	Звено размерной цепи, функционально связанное с замыкающим звеном. Например, звенья Е1 и Е2 размерной цепи Е
Увеличивающее	Составляющее звено размерной цепи, с увеличением которого замыкающее звено увеличивается. Например, звено размерной цепи
Уменьшающее	Составляющее звено размерной цепи, с увеличением которого замыкающее звено уменьшается. Например, звено размерной цепи
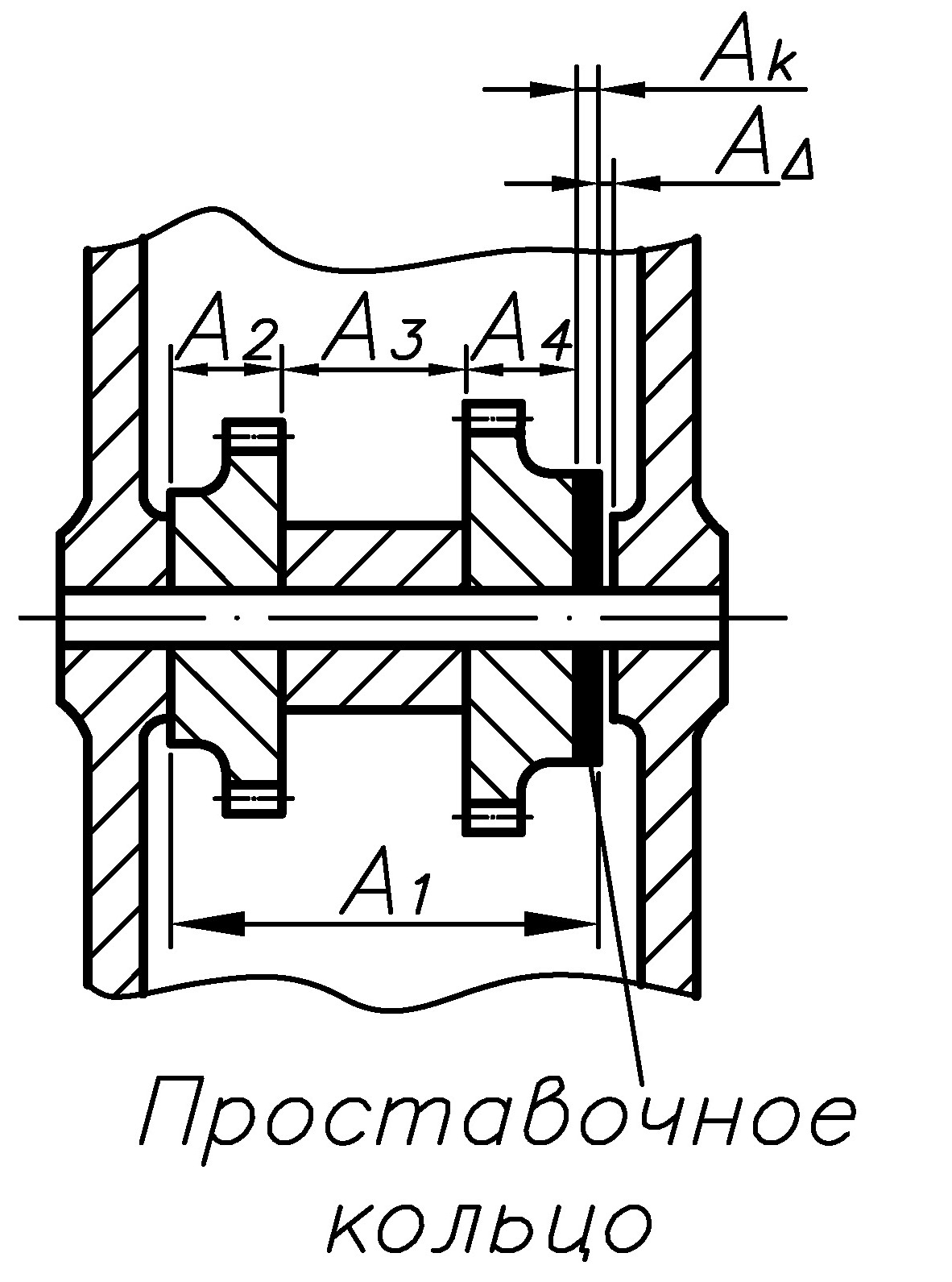
Компенсирующее	Составляющее звено размерной цепи, изменением которого достигается требуемая точность замыкающего звена. Например, звено Ак – проставочное кольцо размерной цепи А

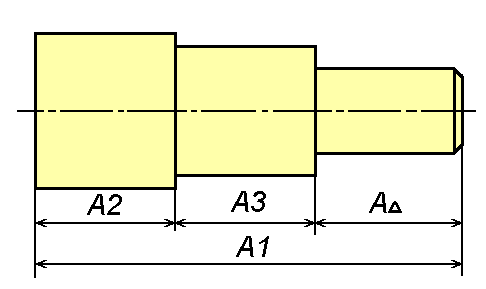
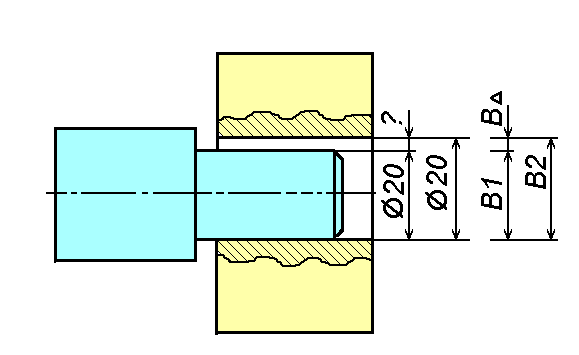
Рис. 2. Размерная цепь детали

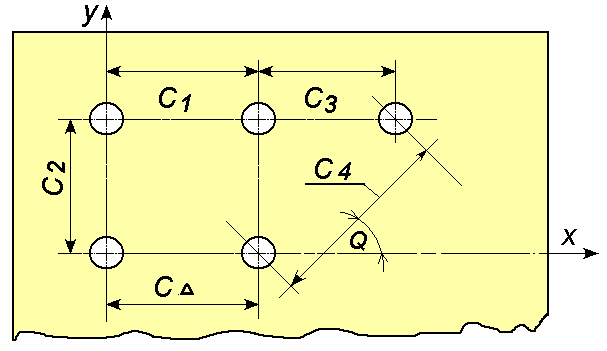
Рис. 3. Размерная цепь узла

Рис. 4. Плоскостная размерная цепь

В табл. 2 показана классификация размерных цепей.

Таблица 2

Виды размерных цепей

Цепь	Определение
Технологическая	Размерная цепь, обеспечивающая требуемое расстояние или относительный поворот между поверхностями изготавливаемого изделия при выполнении операции или ряда операций сборки, обработки, при настройке станка или при расчете межпереходных размеров
Конструкторская	Размерная цепь, определяющая расстояние или относительный поворот между поверхностями или осями поверхностей деталей в изделии
Измерительная	Размерная цепь, возникающая при определении расстояния или относительного поворота между поверхностями, их осями или образующими поверхностями изготовляемого или изготовленного изделия
Линейная	Размерная цепь, звеньями которой являются линейные размеры
Угловая	Размерная цепь, звеньями которой являются угловые размеры
Плоская	Размерная цепь, звенья которой расположены в одной или нескольких параллельных плоскостях
Пространственная	Размерная цепь, звенья которой расположены в непараллельных плоскостях

Увеличивающими называются составляющие размеры, при увеличении которых замыкающий размер увеличивается.

Уменьшающими называются составляющие размеры, при увеличении которых замыкающий размер уменьшается.

Например, достаточно добавить некоторую малую величину к размеру (см. рис. 4), при постоянстве остальных размеров цепи (здесь это только ), чтобы F уменьшился. Если же, оставив неизменным , добавить , то замыкающий F увеличится.

Учитывая разделение размеров на увеличивающие и уменьшающие не трудно записать уравнение размерной цепи в номиналах

А = Ai ув – Ai ум (1)

где в размерной цепи:

m - количество увеличивающих размеров,( Ai ув),

p - количество уменьшающих размеров (Ai ум ).

Всего номинальных размеров составляющих звеньев, с учётом замыкающего, будет: n=m+ p+1

Предельные значения размеров замыкающего звена определяются по уравнениям, логически вытекающим из выражения (1) и определений увеличивающих и уменьшающих размеров:

= – (2)

= – (3)

где: , - наибольший и наименьший предельные размеры замыкающего звена;

, , , - наибольшие и наименьшие предельные размеры звеньев.

Допуск замыкающего размера вычисляется как разность наибольшего (2) и наименьшего (3) значений замыкающего, т. е. достаточно сложить два последних уравнения и получим

TA = TAi (4)

где: TA -допуск замыкающего размера;

TAi - допуск составляющего размера;

n–1 - количество составляющих звеньев размерной цепи, без замыкающего.

В общем случае для размеров размерной цепи A справедливо соотношение:

TA = TAi (5)

где: = передаточное отношение, n – число звеньев цепи.

Если же проводится анализ цепей с параллельными звеньями, то:

для увеличивающих размеров =+1,

для уменьшающих размеров =-1.

Параметр наиболее необходим при формализации решения задач, например при программировании.

Предельные значения составляющих размеров и замыкающего звена в случае, если размеры заданы номинальными значениями и отклонениями, определяются по формулам:

= Аi + ESi

= Аi + EIi

= А + ES (6)

= А + EI, (7)

где: Аi , А - номинальное значения составляющих и замыкающего размера,

ESi, EIi, ES, EI - верхнее и нижнее отклонения составляющих и замыкающего размера.

Воспользуемся уравнением

= –

Запишем его с учётом рассмотренных выше определений предельных значений

А + ES = (Аiув + ESiув)– (Аiум + EIiум)

Подставим в левой части уравнения

А = Ai ув – Ai ум

Верхнее и нижнее отклонения замыкающего размера в этом случае определяются по уравнениям размерной цепи в отклонениях:

ES = ESi ув – EIi ум (8)

EI = EIi ув – ESi ум, (9)

где: ESi ув , EIi ув , ESi ум , EIi ум - верхнее и нижнее отклонения увеличивающих и уменьшающих составляющих звеньев размерной цепи.

При решении ряда задач по размерному анализу верхнее и нижнее отклонения замыкающего размера удобнее определять по формулам через координату середины поля допуска:

ES = 0 А + (10)

EI = 0 А – , (11)

где: 0А - TА - допуск на замыкающее звено, определяемый по формуле (5).

Координата середины поля допуска замыкающего звена, определяется по уравнению середин полей допусков размерной цепи:

0 А = 0 Аi ув – 0 Аi ум, (12)

где: 0 Аi ув , 0 Аi ум - координаты середины поля допуска составляющих звеньев размерной цепи, определяемые по зависимости:

0 Аi = (ESi + EIi)/2

С учётом выражений(11) и (12), верхнее и нижнее отклонения замыкающего размера определяются по формулам:

ES = (0 Аi ув – 0 Аi ум) + (13)

EI = (0 Аi ув – 0 Аi ум) – (14)

Известно, что величина допуска каждого составляющего размера определяется по формуле:

TAi = a i ii,

где: a - коэффициент точности; ii = 0.45+ 0.001Ai ср - единица допуска.

Но следует полагать, что все составляющие звенья цепи одного уровня точности, что позволяет записать:

a 1 = a 2 = a 3 = a 4 =…= a n-1 = a = const

Тогда:

TAi = a (0.45+ 0.001Ai ср),

Ai ср - средний размер интервала размеров.

Учитывая уравнение (5) ТА = TAi,

Или

ТА = a i1 + a i2 + … a in-1= a

теперь можно записать:

Если же изначально в размерной цепи некоторые размеры были с заданными допусками (например, размеры подшипников и т.д.), то уравнение (5) примет вид:

Здесь к – число размеров с заданными допусками. Теперь окончательно уравнение для коэффициента точности будет:

(15)

Определив коэффициент точности, можно вычислить допуски как TAi = а·ii, но рациональнее по таблице допусков выбирать допуски по ближайшему квалитету. В случае одинаковых размеров составляющих звеньев или же размеров находящихся в стандартном интервале размеров, где «i» неизменно для интервала, формула упрощается

или TАi = ТА/(n-1) (16)

Как видно получен единый допуск для всех размеров. Способ этот прост, но по сути ориентировочный и поэтому применяется, в основном, лишь для предварительного назначения допусков составляющих размеров.

Допуски для размеров назначают, как для основного вала и основного отверстия, т.е. для увеличивающих в «+» а уменьшающих в «-», за исключением увязочного. Для увязочного размера положение допуска определяется по одному из уравнений, связывающих параметры замыкающего размера и составляющих, при назначенных параметров остальных.

Приведённые зависимости справедливы для метода полной взаимозаменяемости (МПВ), где предполагается равновероятное распределение получаемых размеров. Иначе говоря, при стрельбе в круглую мишень с прицеливанием в середину мишени, вероятность попадания в «1» и в «10» одинакова, что не совсем верно.

Теоретико-вероятностный метод (ТВМ)

Теоретико-вероятностный метод (ТВМ) основывается на вероятностных кривых распределения и как результат применяет несколько отличные формулы (здесь приводим без вывода). В представленных зависимостях предусмотрено равновероятностное распределение и коэффициент риска 0.27%.

…………………………(17)

…………………………(18)

Значение допуска увязочного размера в ТВМ определяется по зависимости

…………………………(19)

Из формул не трудно заметить, что для ТВМ допуски будут шире, чем для МПВ

Метод компенсации

В методе регулирования точность замыкающего звена размерной цепи достигается изменением размера компенсирующего звена без удаления материала с компенсатора.

Подвижные компенсаторы - это устройства или отдельные детали, за счет регулировки которых, достигаемой перемещением или поворотом, обеспечивается требуемый размер замыкающего звена (рис.5).

Неподвижные компенсаторы это, например сменные прокладки, кольца, втулки, шайбы и т.д., устанавливаемые при сборке до достижения требуемой точности замыкающего звена. Рационально готовить наборы компенсаторов одинаковой или ступенчатой толщины (рис.6).

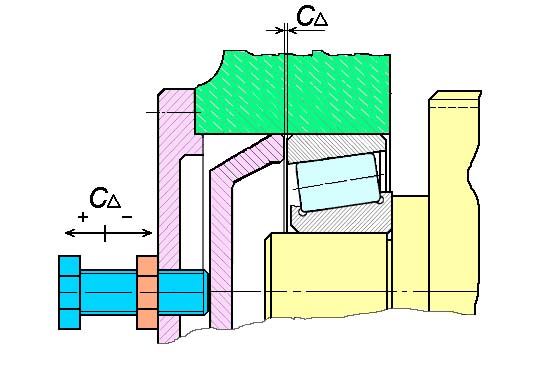
Рис. 5. Подвижный компенсатор

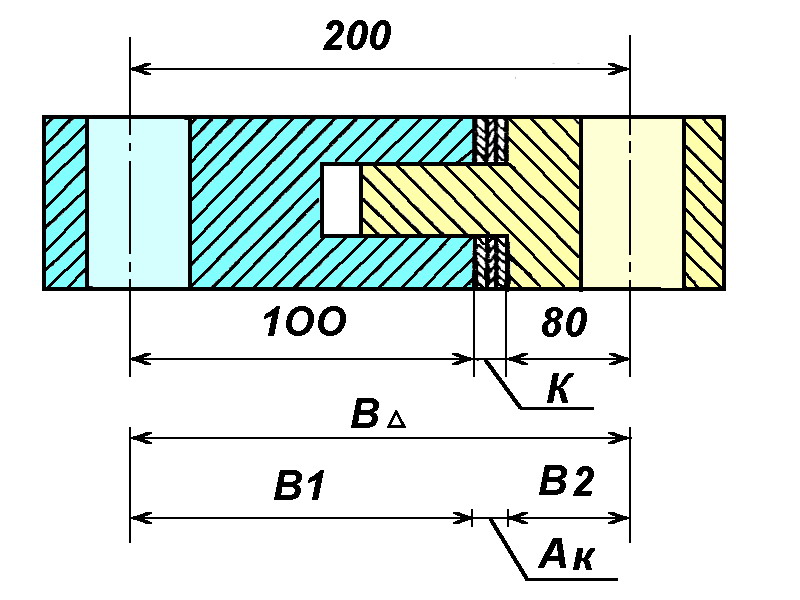
Рис. 6. Неподвижный компенсатор

Подвижные компенсаторы по непрерывности регулирования разделяют на компенсаторы с периодическим регулированием (резьбовые, клиновые, эксцентриковые и др.) и компенсаторы с непрерывным регулированием, как правило, автоматического регулирования технологического процесса. По назначению все типы компенсаторов делят на группы, компенсирующие линейные или угловые размеры. Расчет параметров размерных цепей проводят методом максимума-минимума или вероятностным методом.

К недостаткам метода регулирования относят: неполную взаимозаменяемость, некоторое усложнение конструкции введением конструктивного компенсатора и усложнение сборки из-за необходимости проводить регулировку. Метод нашел широкое применение для многозвенных цепей с высокими требованиями к точности замыкающих звеньев и не столь высоким уровнем точности составляющих звеньев.

Параметры составляющих звеньев размерной цепи при методе регулирования назначают в соответствии с технологически и экономически приемлемыми условиями производства. Требуемая при этом величина компенсации ТАк достигаемая регулированием при помощи рассмотренных выше типов компенсаторов.

Запишем уравнение

Приняв технологически и экономически целесообразные расширенные допуски можем получить

Введя Ак и ТAк можно обеспечить равенства

При теоретико-вероятностном методе

Для обеспечения необходимой точности замыкающего звена в методе регулирования размер минимальной ступени компенсаторов не должен превосходить допуска замыкающего звена:

При равенстве можно определить необходимое число ступеней компенсации

Полученное значение N определяет потребное число прокладок с некоторым запасом.

На этапах производства и эксплуатации конструкции возникает необходимость решение обратных задач, когда вычисляют параметры замыкающего звена по известным (заданным) параметрам всех составляющих звеньев размерной цепи. На этапе проектирования обратные задачи решаются с целью проверки правильности решения прямых задач.

В методе пригонки необходимая точность замыкающего звена размерной цепи, получается, посредством удаления с компенсатора некоторого слоя материала, для достижения размера компенсирующего звена. Для этого компенсирующее звено детали компенсатора поступает на сборку с заранее установленным припуском, который удаляется, методами механической обработки для достижения требуемого значения замыкающего звена. Этот метод позволяет установить экономически целесообразные допуски на все составляющие звенья размерной цепи. Однако следует заметить, что применяется он только в индивидуальном и мелкосерийном производстве. К недостаткам метода относят удорожание сборки и повышенную трудоемкость сборочных работ, а также усложнение планирования и снабжения изделия запасными частями.

Для усвоения теоретических зависимостей попробуем решить размерную цепь простого узла различными методами.

Селективная сборка

Сущность селективной сборки состоит в том, что детали соединения изготавливают с технологически выполнимыми и экономически целесообразными допусками. Изготовленные детали измеряют и сортируют на группы по действительным размерам. Сборку соединений производят по одноименным группам.

Селективной называют сборку изделий из деталей, предварительно рассортированных на группы по их действительным размерам. Этот метод применяют, для различных соединений в том числе и при решении размерных цепей и называют также методом групповой взаимозаменяемости. Селективная сборка позволяет увеличить точность замыкающего звена размерной цепи без увеличения точности обработки составляющих звеньев. Можно уменьшить точность изготовления составляющих звеньев узла и посредством селективной сборки получить потребный допуск замыкающего размера. Cборка узлов производится из одноименных групп. В некоторых случаях получение изделий в массовом производстве без применения селективной сборки вообще невозможно. Например, подшипники качения, ответственные резьбы с натягом, точные поршневые группы, топливные насосы дизелей, и другие высокоточные изделия можно получить только с помощью селективной сборки.

Селективную сборку применяют:

- с целью повышения точности замыкающего размера без уменьшения допусков на детали, образующие узел;

- с целью расширения допусков на обработку при сохранении заданной точности замыкающего размера.

Основное достоинство селективной сборки - снижение затрат и получение требуемой точности сопряжения, достижение которой технологически затруднительно или невозможно.

Недостатки селективной сборки:

- дополнительные затраты на измерение деталей, сортировку, маркировку, хранение;

- обеспечивается неполная (групповая) взаимозаменяемость.

- возникает незавершенное производство в результате разного количества деталей в одноименных группах сортировки.

- рациональность применения при крупносерийном и массовом производстве.

Пример: необходимо изготовить для сборки с указанным зазором.

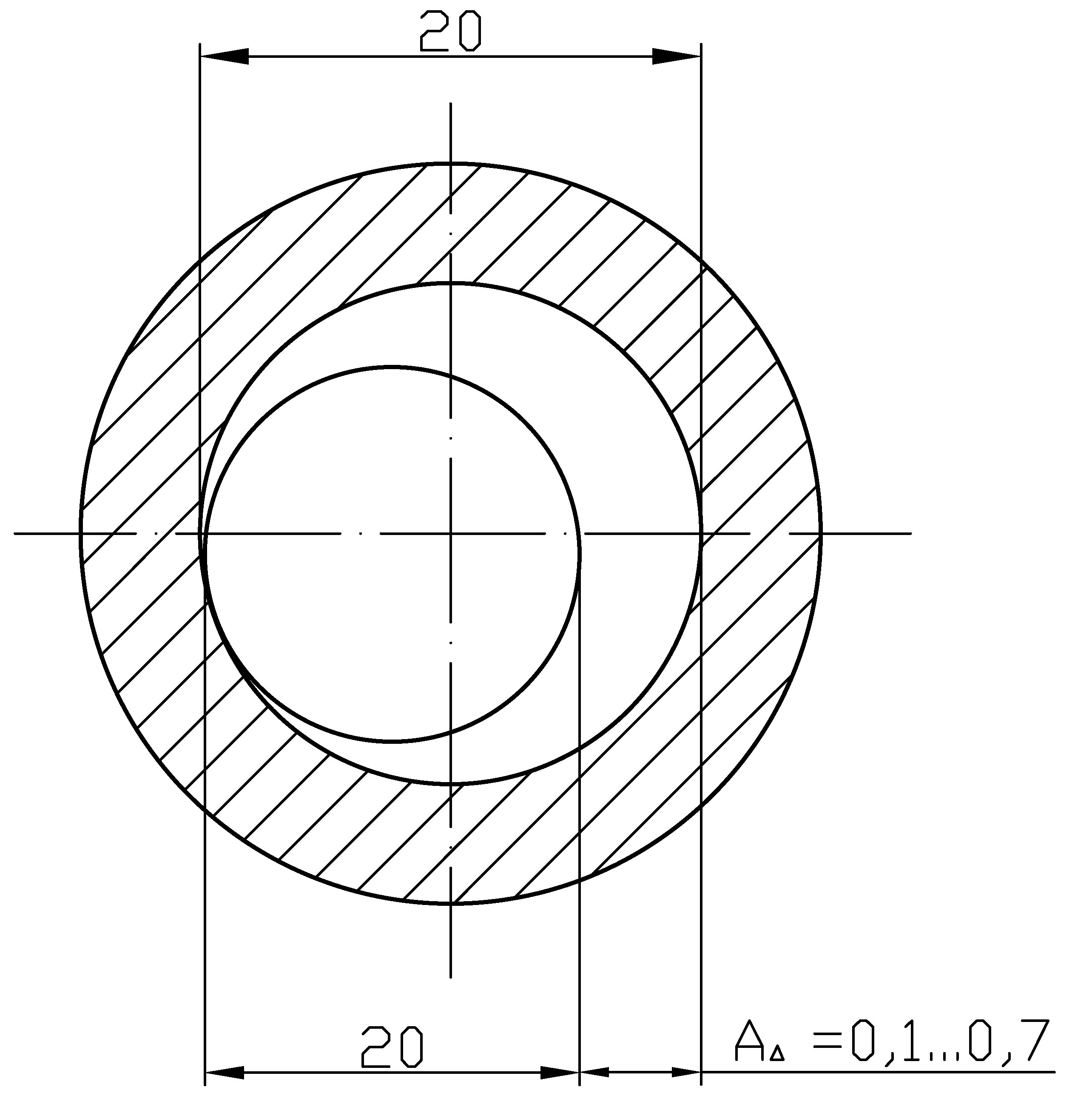
Выделим размерную цепь узла:

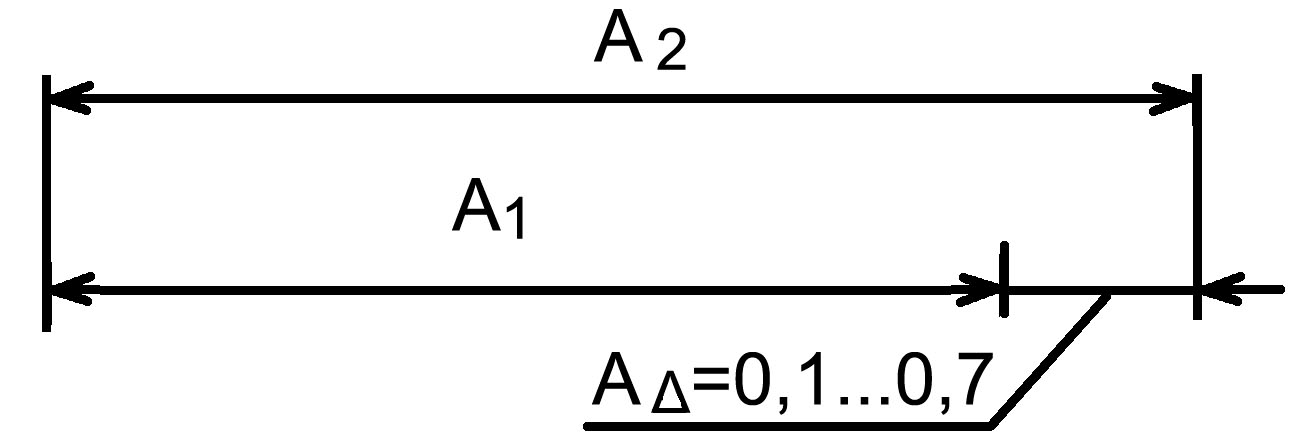
где n=3,число размеров

m=1,увеличивающих

n=1,уменьшающих

Допуск замыкающий

TA=ES-EI=0,7-0,1=0,6

Допуск составляющих

TAi=

Tai=T1A2=300 мкм

А2 увеличивающий, А1 уменьшающий. Для А2 назначим допуск в тело от нуля и поэтому A2=20+0,3, за увязочный примем А1 по уравнению ES=-

ES=ESA2-EIA1; EIA1= ESA2- ES

EIA2=0,3-0,7=-0,4 мм

ESA2= EIA2+ТА2=-0,4+0,3=-0,1 мм

Тогда А2=

а)Условия сборки узла изменились и необходимо получить ТА=300 мкм.

Можно заказать новую партию деталей с более жестким допуском.

Но не изготавливая вновь детали можно разделить партию на 2 группы:

А1=20 А1=20 ТА=300 мкм

А2=20 А2=20 ТА=300 мкм

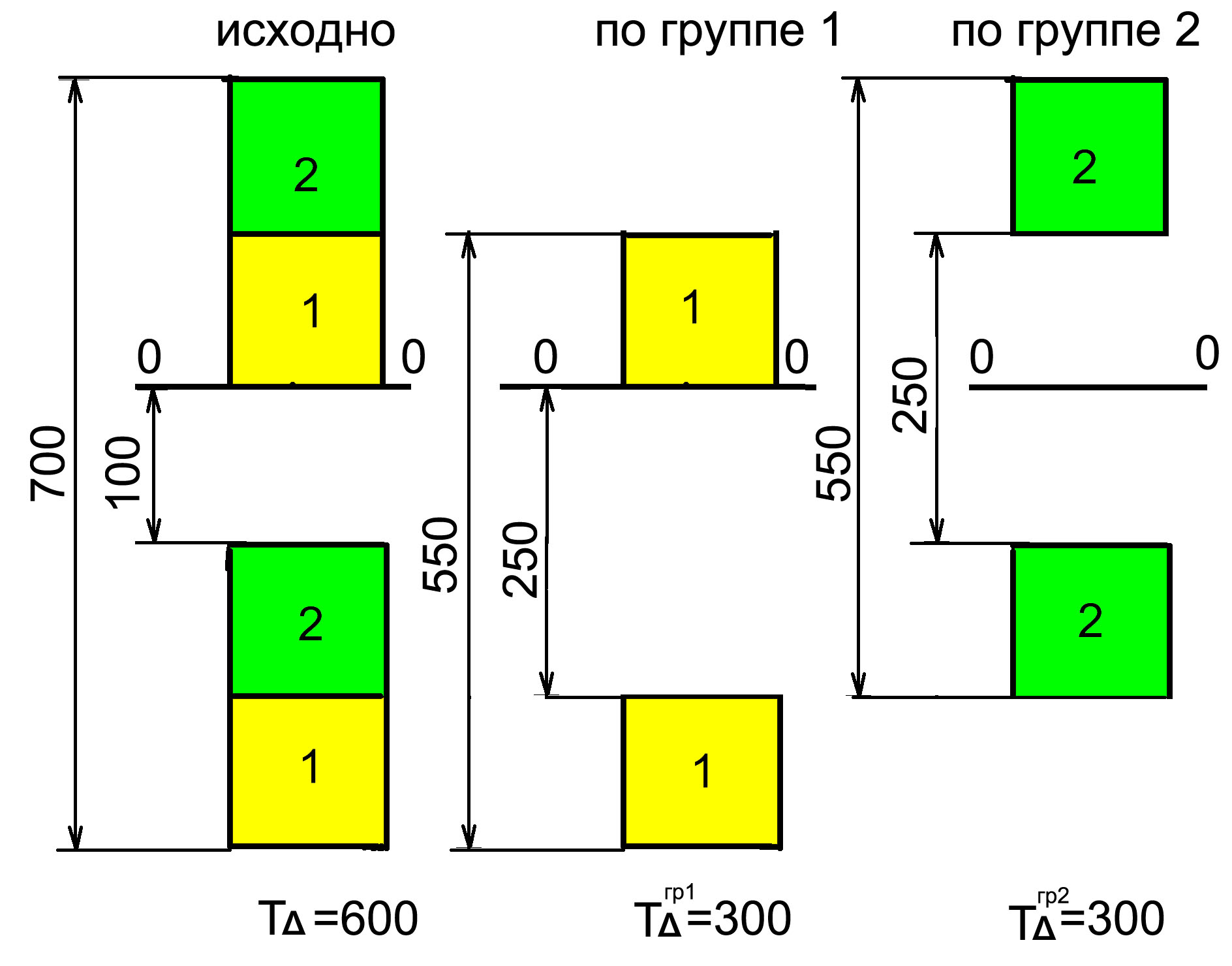
Данное решение получено в предположении, что количество валов и отверстий по группам одинаково, что не всегда так при мелкосерийном производстве, массовое производство позволяет получать практически, собирать 100 % изделий.

б)условия производства изменились и не позволяют изготавливать изделие с TA=0,6 мм. В этом случае можно изготовить узел с TA=1,2 мм, а затем, аналогично разделив серию деталей на 2 группы получить в сборке TA=0,6 мм.

Примеры решения задач размерных цепей различными методами

Задание:

Для узла на первом рисунке провести сравнительный расчет размерной цепи различными методами.

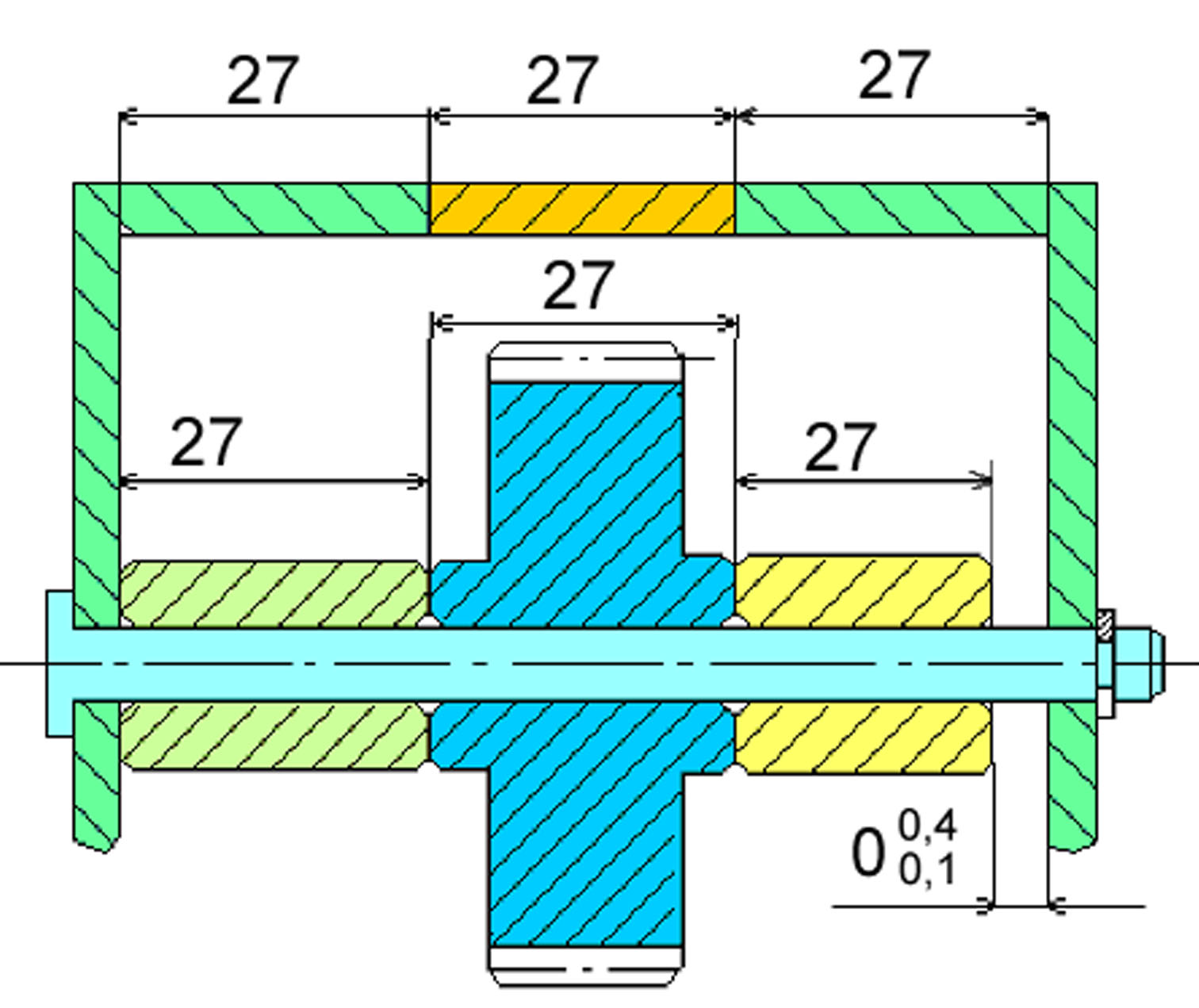
Рисунок . Узел 1.

Выделим размерную цепь из узла:

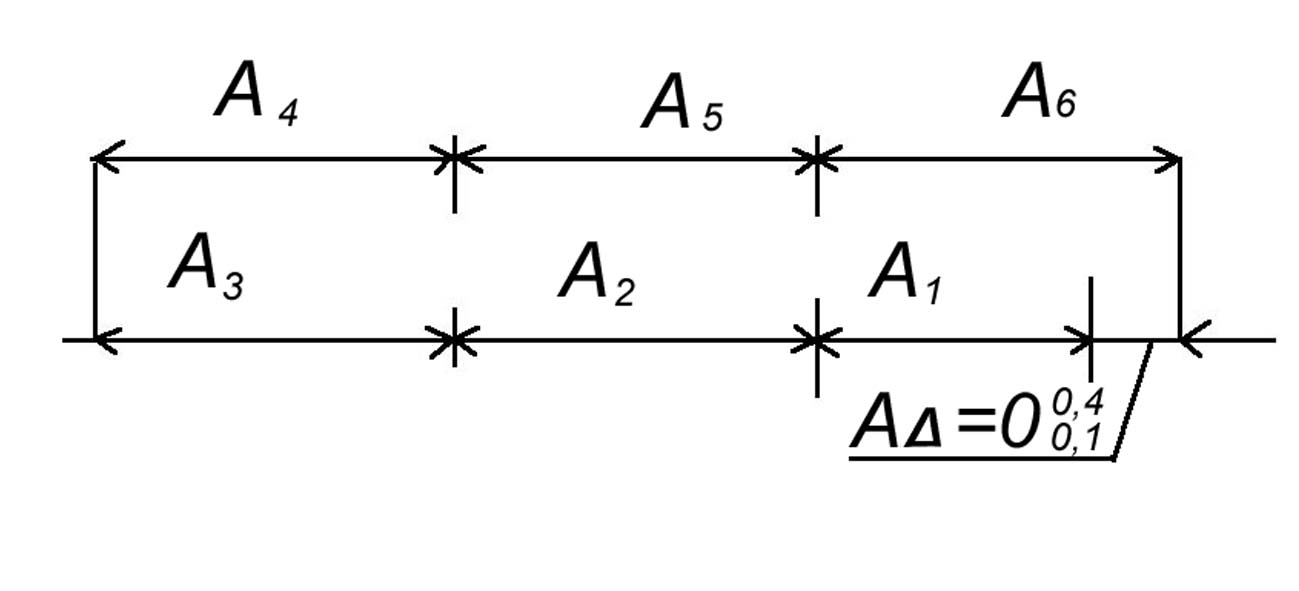
Рисунок . РЦ-А

Всего размеров в размерной цепи n = 7, n = m + p,

где: m -увеличивающих, p-уменьшающих

Увеличивающие размеры А4, А5, А6, уменьшающие размеры А1, А2, А3

По способу равных допусков

Применим формулы:

TAi=TAD/ (n-1), TAi=300мкм/ (n-1) =50мкм

Воспользуемся уравнением:

= –

Выбрав в качестве увязочного размера, примем уменьшающий , получим:

= – –

Представим графически положение допусков, приняв их в тело детали для всех размеров, кроме увязочного:

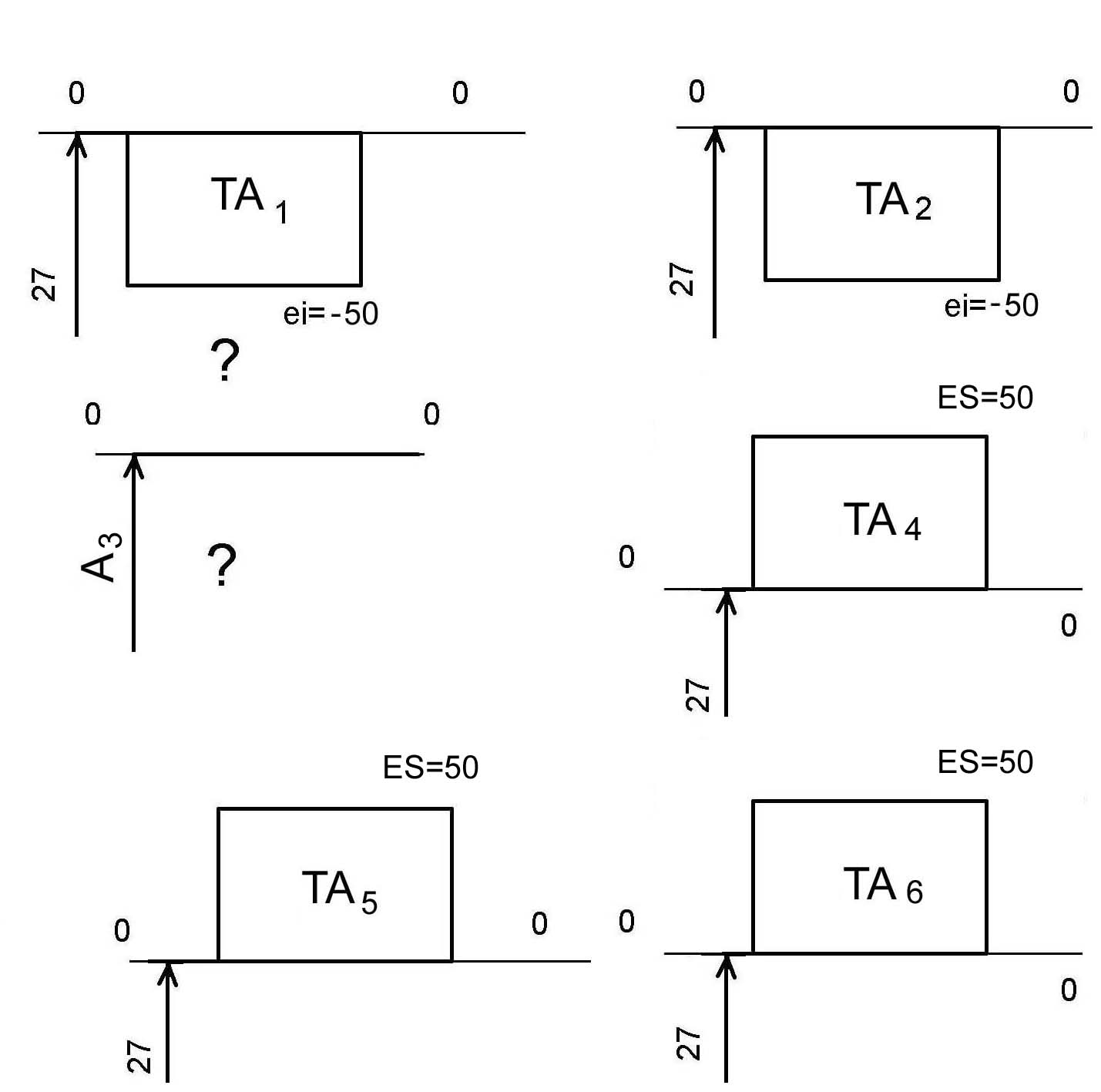
Рисунок . Поля-А

Найдем его наименьшее значение :

=26,850

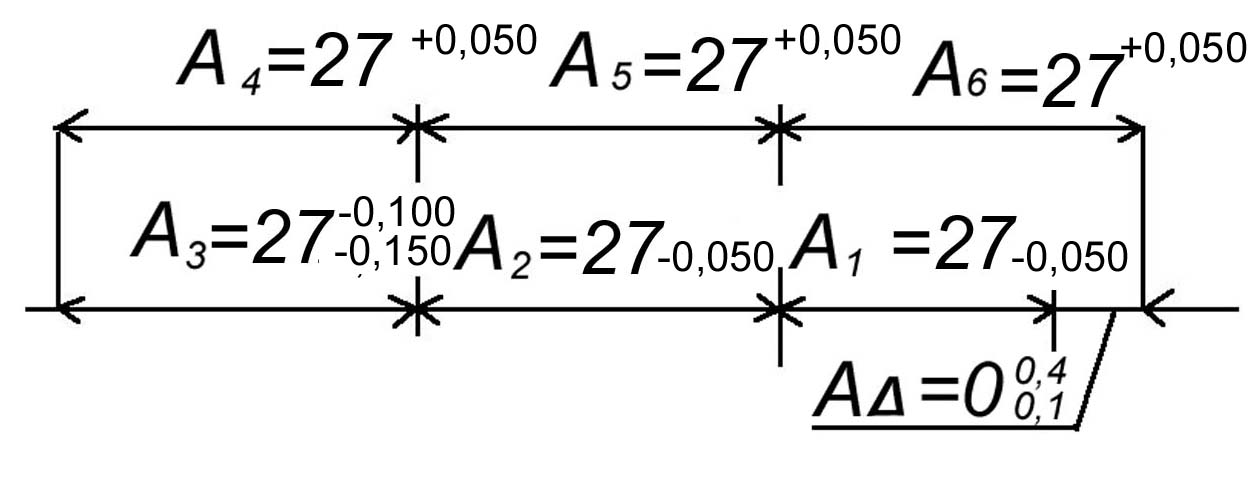
Рисунок . РЦ-А с отклонениями

В сборке допуски графически можно представить в виде:

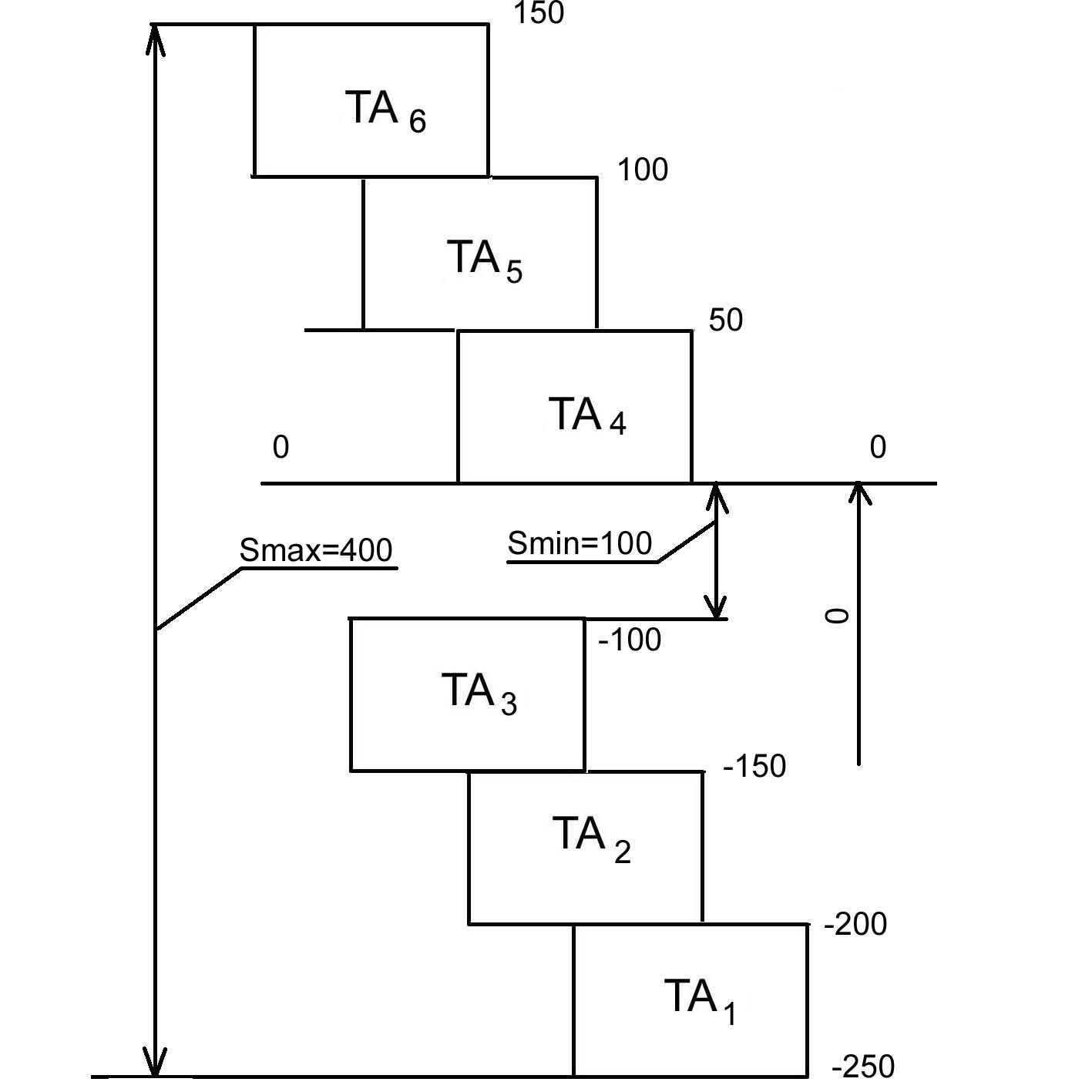
Рисунок . Графическая цепочка полей допусков А

Представим детали узла 1 с номинальными размерами и допусками, подготовленными к сборке. Получим в графической цепочке, как и было, заказано: Smax=400мкм и Smin=100мкм.

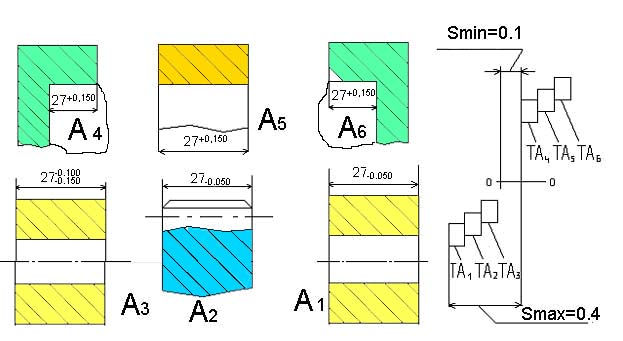
Втулка Шестерня Втулка

Рисунок . Составляющие детали узла с допусками размеров и цепочка их расположения

Решение задачи по методу допусков одного квалитета-полной взаимозамеряемости (МПВ).

Решим ту же задачу, но по зависимостям метода полной взаимозаменяемости, не находя допуски по зависимости способа одного квалитета. При определении допуска, для размерной цепи «А» воспользуемся формулой для расчета допуска через коэффициент точности «а»:

Необходимо определить а и i :

Полагая, что точность изготовления всех деталей одного уровня, можно считать все коэффициенты точности одинаковыми равными аср. Этот коэффициент можно получить:

Если же есть детали с заданными допусками, то формула принимает вид:

-допуски готовых деталей, например полученных по кооперации. У нас заданных допусков нет, поэтому вторая сумма в числителе равна нулю. Допуск замыкающего размера будет:

Теперь допуски размеров будут:

что соответствует результату, ранее полученному по способу равных допусков.

В общем случае метод допусков одного квалитета предполагает наличие различных размеров звеньев. Для ранее рассмотренной задачи будем считать, что корпус целиковый и внутренний его размер 81мм.

Для узла 2 выделим размерную цепь обозначив её «В»: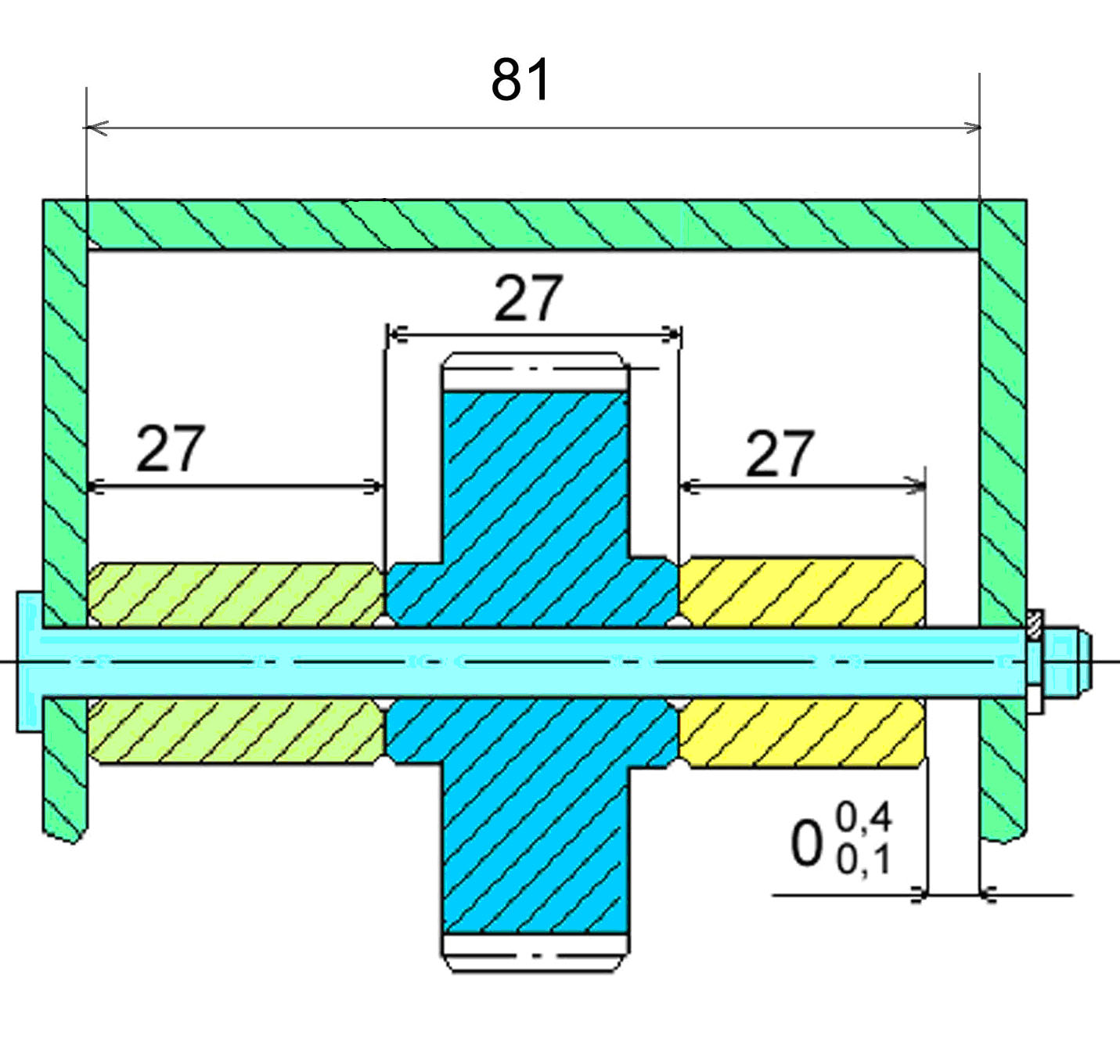

Рисунок . Узел 2.

Теперь размерная цепь примет вид:

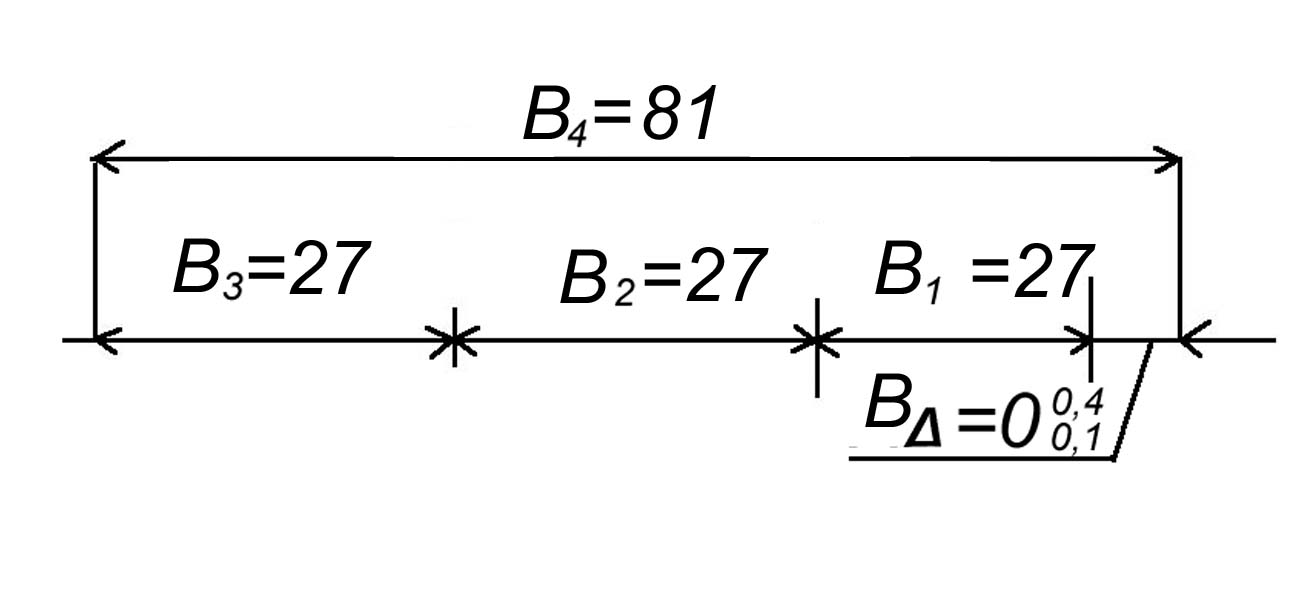
Рисунок . РЦ-В

Размеров с заданными допусками нет, поэтому:

Проверим сумму допусков:

67,07+67,07+67,07+98,781=201,444+98,549=299,871

Округлим допуски до 67 и 99мкм, получим:

67+67+67+99=300

Примем допуски размеров B1, B2, B3 в тело допуска, а B4 как увязочный размер:

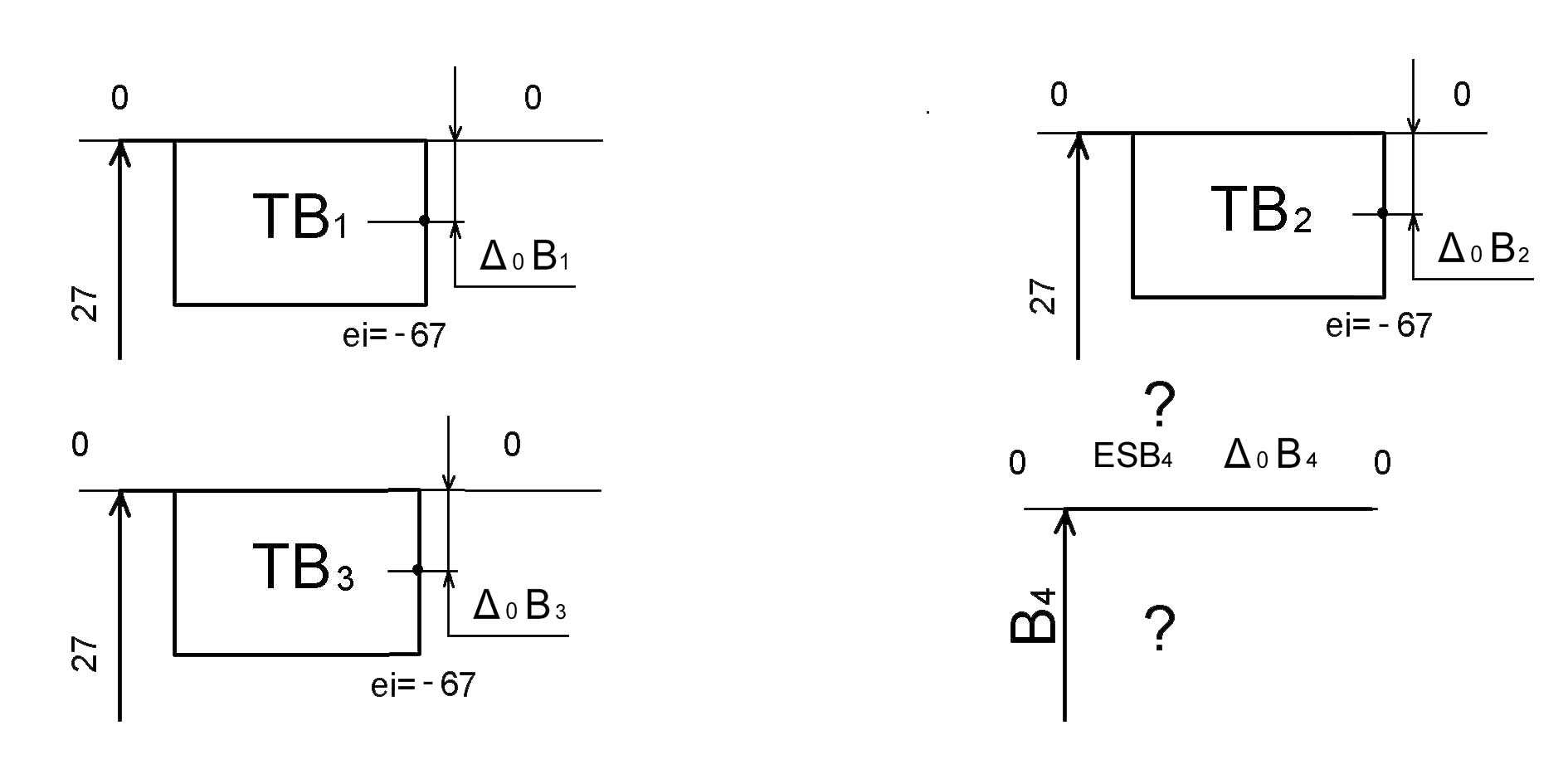
Рисунок . Поля-В

Воспользовавшись уравнением для максимального значения замыкающего размера, получим:

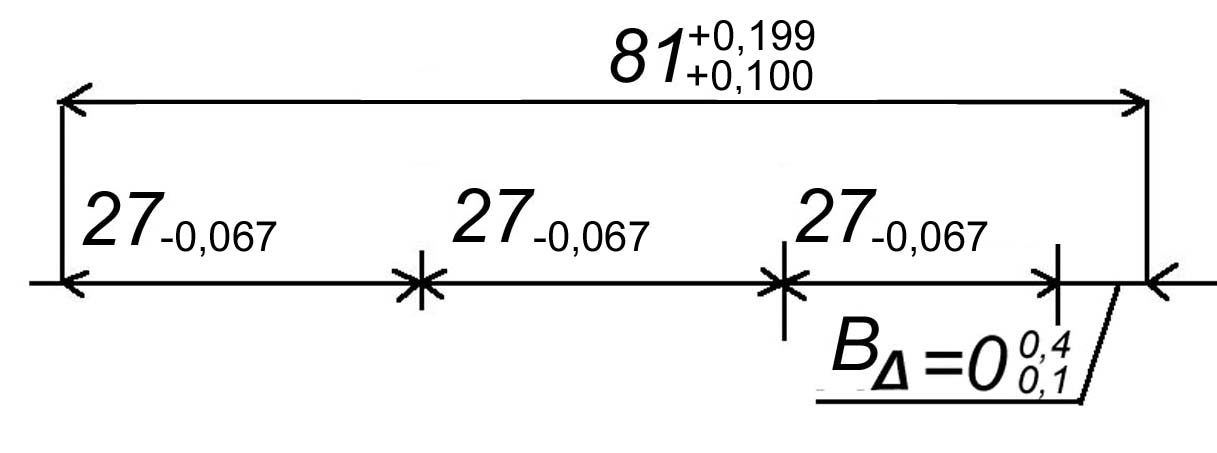
Рисунок . РЦ-В с отклонениями размеров

Теперь, представив, полученный результат графически и проверим полученные величины замыкающего размера:

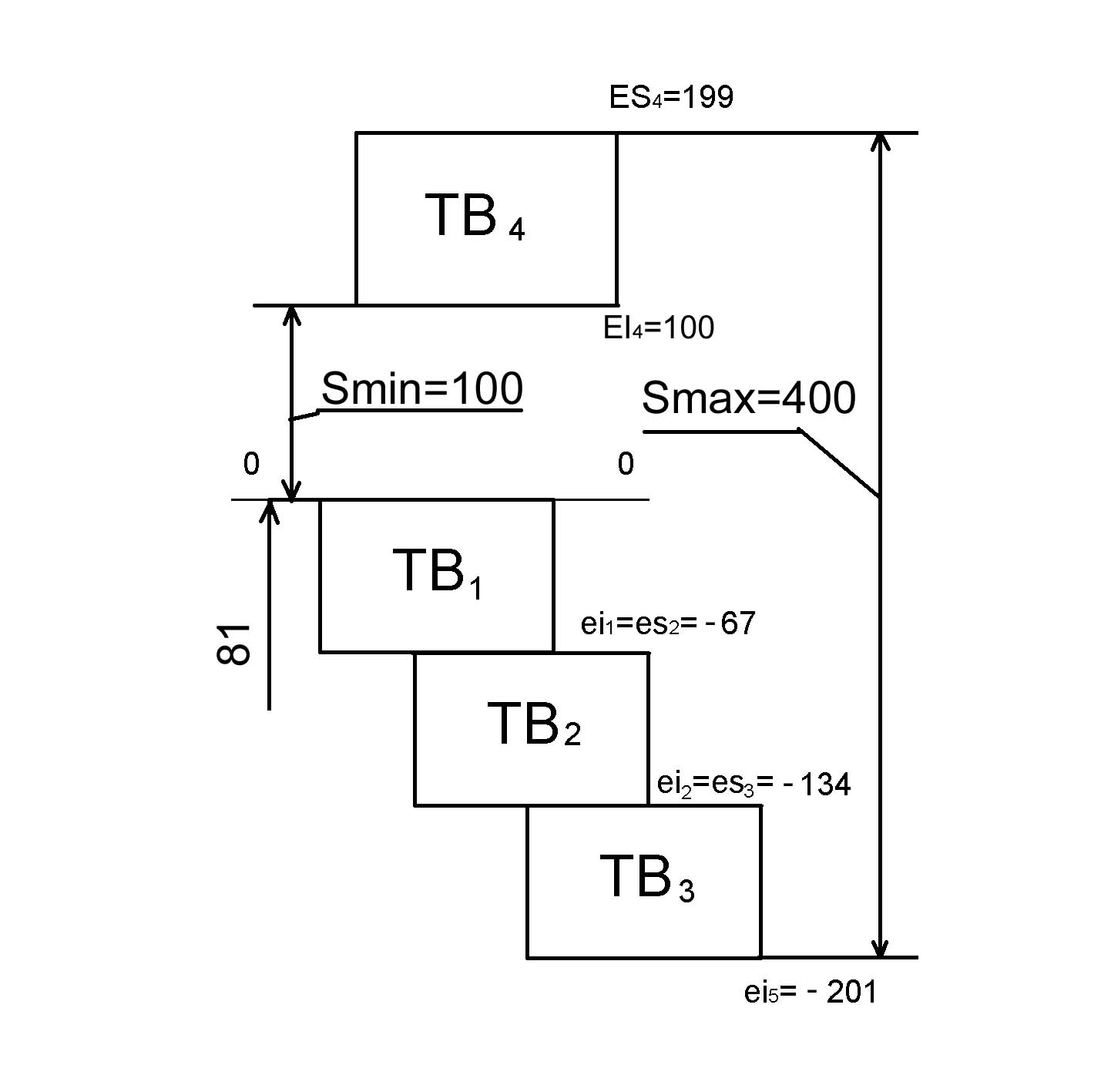
Рисунок . Графическая цепочка полей допусков В

По уравнениям можно тоже провести проверку:

По результатам решения уравнений и графически видно, что задача решена, верно.

Проведём, однако, дополнительно проверку посредством уравнения середины полей допусков:

Здесь обозначено 0 – середина поля допуска соответствующего размера.

Найдём середины полей известных допусков, за исключением увязочного и обозначим значения на рисунке:

Расположение допусков одинаково, поэтому:

Определим середину поля допуска замыкающего размера:

Подставив величины в уравнение, найдём середину поля допуска увязочного размера :

По графической проверке также:

Определим отклонения увязочного размера:

Определим среднюю величину зазора, через допуски по графической цепочке: (100+199)/2+(0+201)/2=149,5+100,5=250мкм

Решение задачи теоретико-вероятностным методом (ТВМ).

Для узла 2 выделим размерную цепь обозначив её «С» :

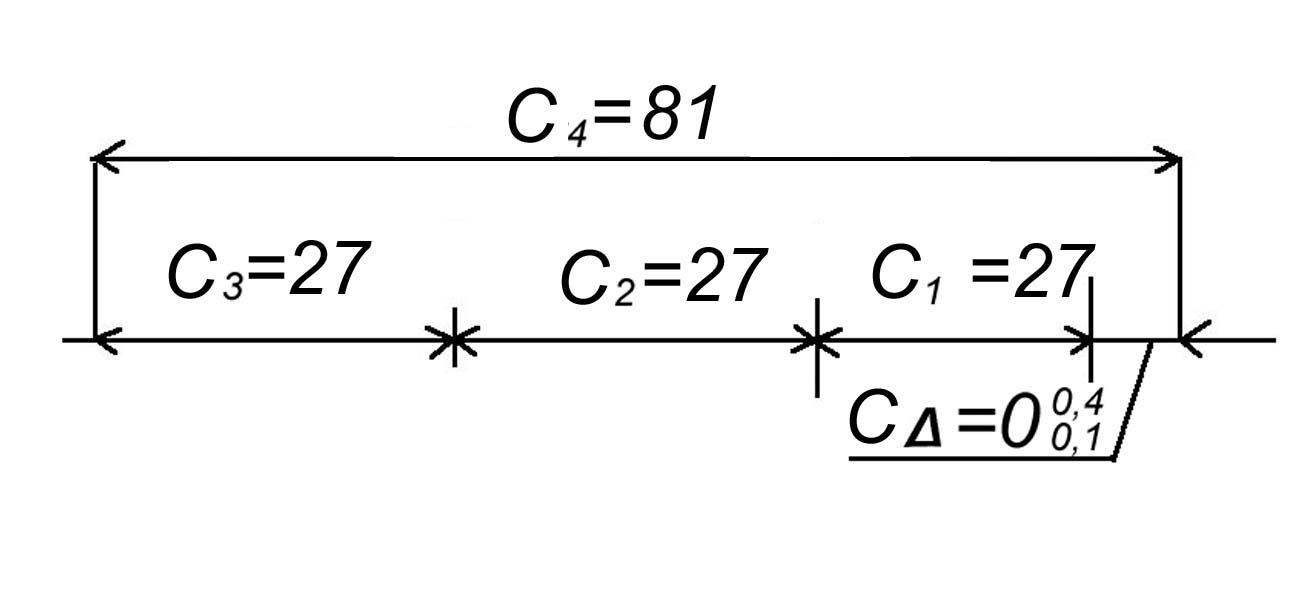
Рисунок . РЦ-С

Задача может быть решена по теоретико-вероятностному методу, для которого связь замыкающего размера с составляющим будет:

Коэффициент точности «а» примет вид:

Квалитет уже больший, чем в МПВ, и можно вычислить допуски и представить положение полей, для всех размеров, кроме увязочного:

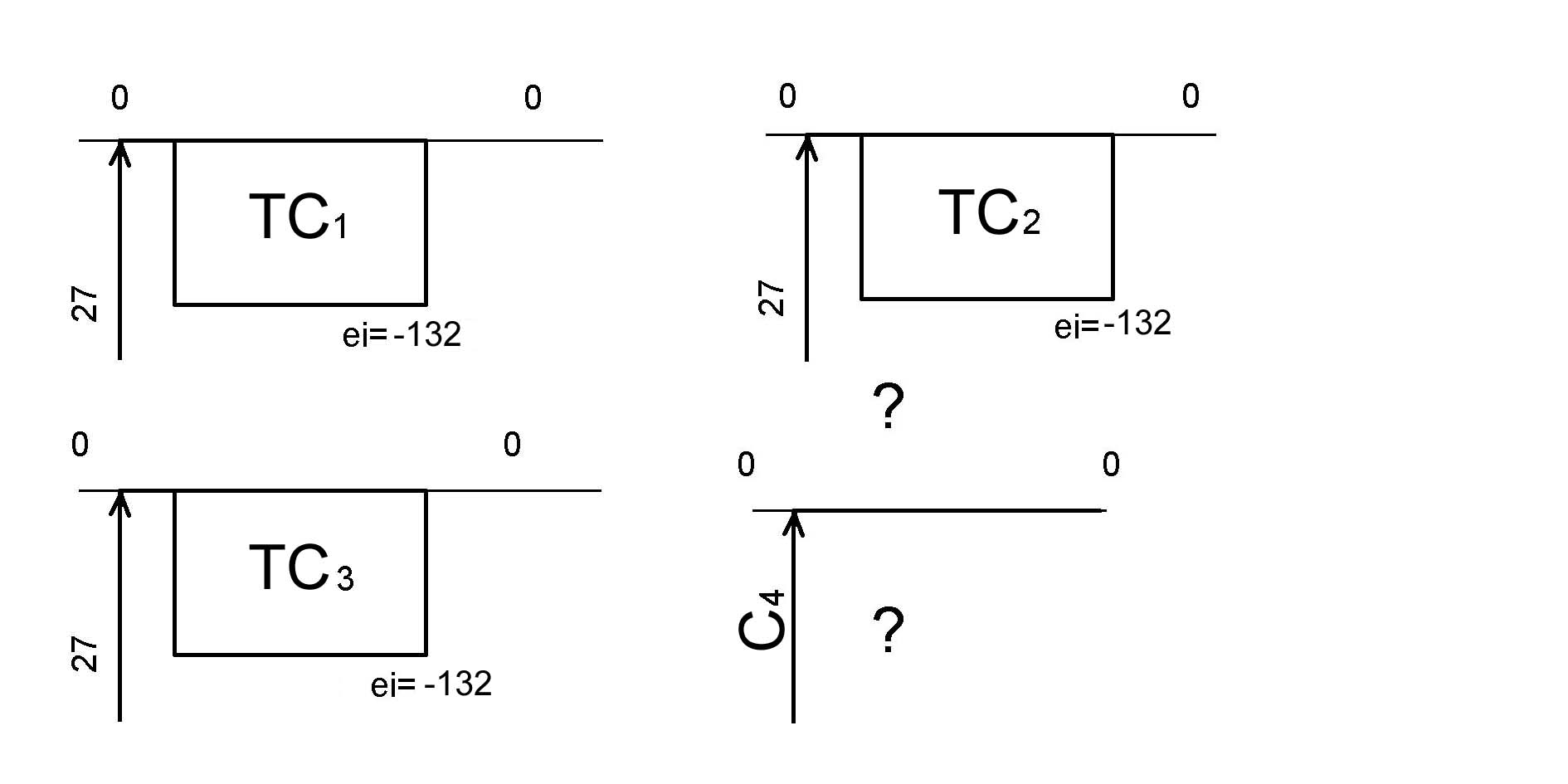
Рисунок . Поля С

Воспользуемся уравнением:

и определим допуск увязочного размера:

Определим середины полей допусков составляющих звеньев РЦ и замыкающего размера для того, чтобы воспользоваться уравнением:

Уравнение середин полей допусков запишем через допуски размеров:

Величина средневероятного зазора будет:

Окончательно размерная цепь будет:

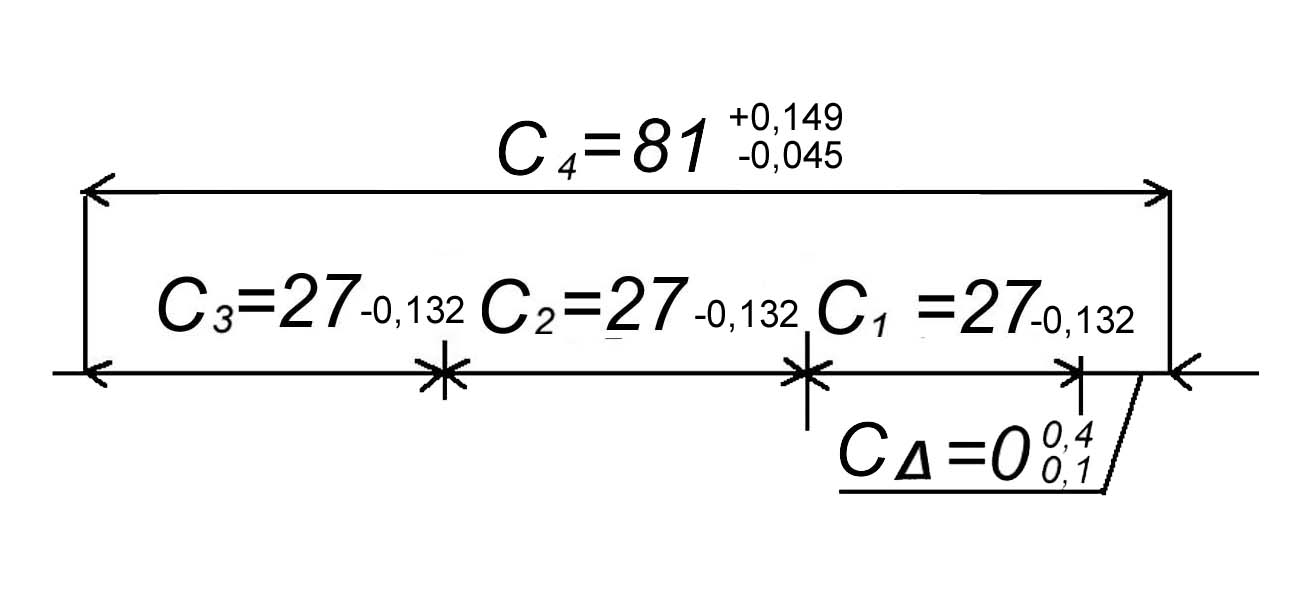
Рисунок . Окончательная размерная цепь «С»

Как видно средняя величина зазора 250 мкм осталась такой же, что и была в решении методом полной взаимозаменяемости (МПВ), а вот допуски взросли и существенно.

Полученные результаты расчета теоретико-вероятностным методом (ТВМ) можно представить графически:

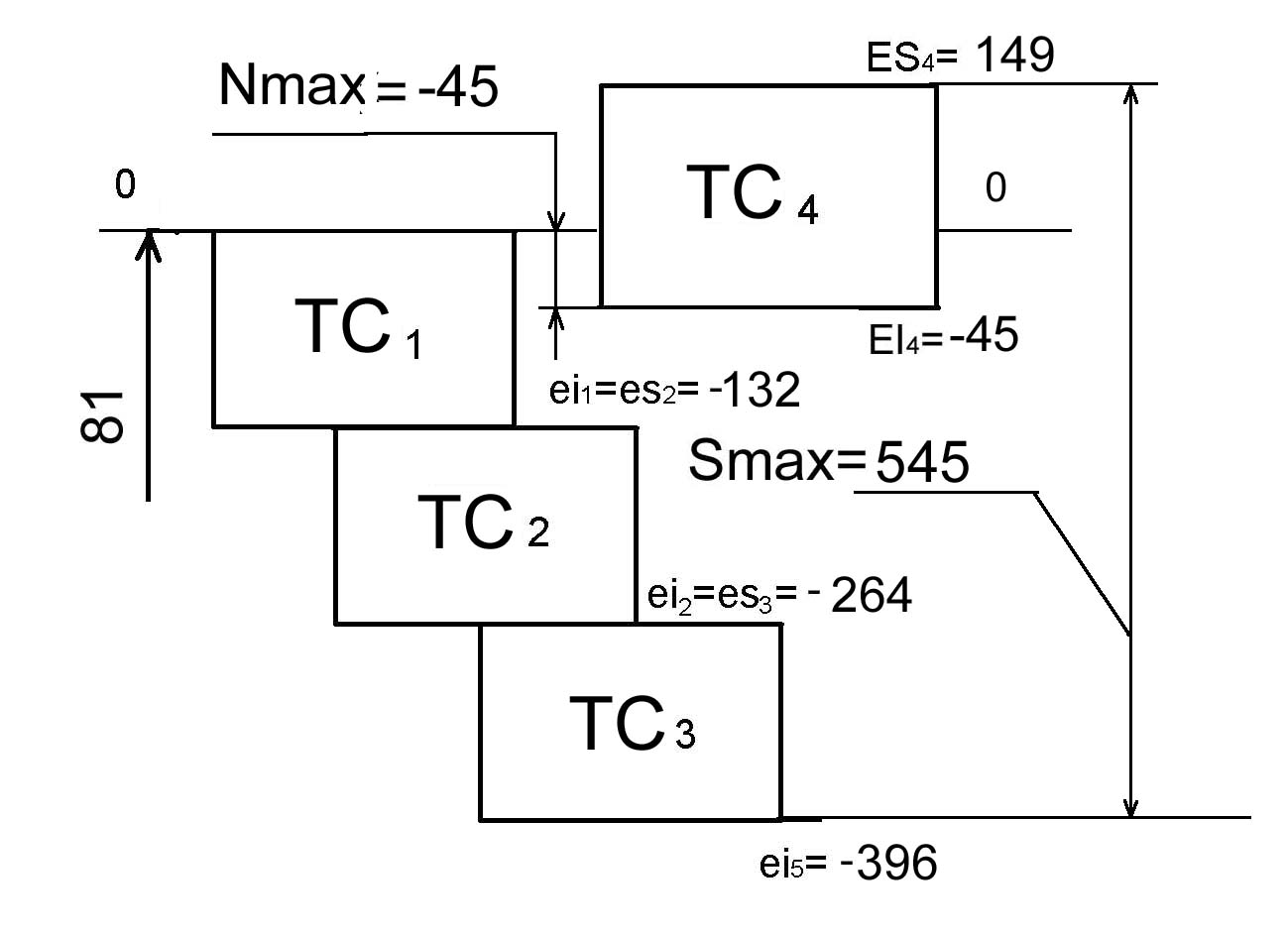
Рисунок . ЦЕПОЧКА С

Оценив соотношения допусков, получим коэффициент расширения допусков, для ТВМ по отношению к МПВ: К1=К2=К3=132/67=1,97 К4=193/99=1,94 Кср=(1,97+1,94)/2=1,95. Теперь достаточно вспомнить о кривой зависимости допуска Т и стоимости деталей С, чтобы заметить, что стоимость производства упадет не в 2 раза, а существенно больше при вероятности несобираемости узла на уровне 0,27% (всего лишь 3 сборки на 1000 не соберутся). И, конечно же, нет сомнений в том, что потери в 3 сборки уже окупились.

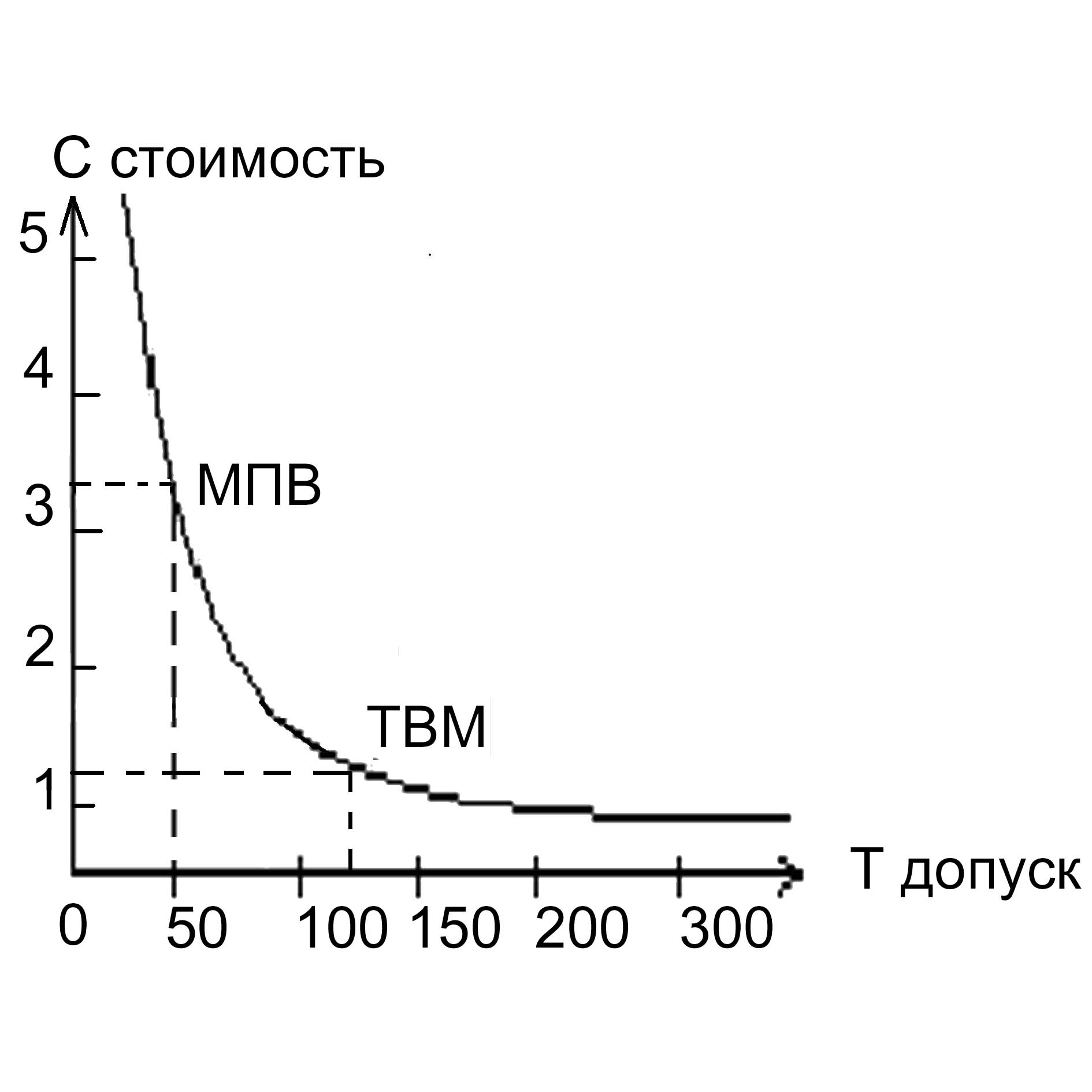
Рисунок . Соотношение величины допусков и стоимости

Решение задачи методом компенсации