СТІЙКІСТЬ АВТОМАТИЧНИХ СИСТЕМ І ПОКАЗНИКИ ЯКОСТІ ПЕРЕХІДНИХ ПРОЦЕСІВ

ЛЕКЦІЯ 4

4.1 Поняття стійкості автоматичних систем керування

Вияснимо фізичне трактування поняття стійкості. Роглянемо кулю, поміщену у верхню точку підвищення. Вона знаходиться в нестійкому положенні. Дійсно, достатньо найменшого відхилення кулі від початкового положення, як вона скотиться по схилу поверхні і не повернеться у вихідне положення.

Навпаки, куля, що знаходиться у впадині, займає стійке положення, і після відхилення вона обов’язково повернеться до свого початкового положення.

Таким чином, стійкість – це властивість системи (куля – поверхня) повертатись у вихідний стан після виведення її з цього стану та припинення дії збурення.

Як видно з визначення, здатність системи повертатись в початковий стан пов’язується з початковими відхиленнями. В розглянутих прикладах стійкість і нестійкість не залежать від початкових відхилень кулі. Але можна уявити собі таку систему, яка при малому відхиленні повертається, а при великому – не повертається у вихідне положення. Прийнято вважати, що така система стійка в малому і нестійка у великому, оскільки стійкість пов’язана з величиною початкового відхилення. Система, з кулею, що знаходиться у впадині є безмежно стійкою, так як куля буде повертатись у вихідне положення при будь-якому початковому відхиленні. Система має властивості байдужої рівноваги.

Чи завжди за вихідний стан системи, стійкість якої оцінюється, беруть стан спокою? Ні, не завжди. В загальному випадку можна говорити про стійкість руху взагалі, тобто руху, пов’язаного з будь-яким переміщенням маси або енергії. Наприклад, можна оцінити стійкість руху супутника, як його здатність повертатись на вихідну орбіту після припинення дії сил, які відхиляли супутник від заданої орбіти. Так само можна оцінити стійкість системи автоматичного управління, як її здатність повертатись до початкового незбуреного руху після припинення дій збурення.

Отже, ми розглянули якісну оцінку поняття стійкості. Але існує і кількісна оцінка цього поняття: стійкість можна описати математичними формулами.

Вперше найбільш суттєві математичні результати по стійкості механічних систем були отримані харків’янином А.М.Ляпуновим у 1880-1910 рр. Оскільки різні за своєю природою матеріальні системи описуються однаковими диференціальними рівняннями, то результати по стійкості механічних систем, отримані А.М.Ляпуновим, можна використати і до інших фізичних систем, в тому числі до систем автоматичного керування.

Стійкість є дуже важливою характеристикою якості систем і пристроїв, що використовуються в різних галузях техніки. Особливо гостро проблема стійкості стоїть в автоматиці. Це пояснюється наступним. Автоматичні системи є замкнутими системами, в яких вихідна величина через основний зворотний зв’язок подається на вхід системи, де порівнюється з заданим впливом. Система, що нормально функціонує, бажає зменшити різницю між значеннями задаючого впливу і керуючої величини. Але інколи виходить так, що ця різниця буде не зменшуватись, а зростати з плином часу, тобто система буде нестійкою. Характерно, що нестійкою може бути система, яка складається тільки зі стійких елементів, як це часто буває на практиці.

Через складність автоматичних систем для оцінки їх стійкості тільки фізичних уявлень недостатньо. Для цього необхідне використання математичного апарата. Тому розглянемо, в чому полягає особливість математичного трактування стійкості автоматичних систем.

4.2 Математична оцінка стійкості

Математично стійкість незбуреного руху оцінюють за характером збуреного руху як здатність системи приходити в результаті збуреного руху до незбуреного руху, якщо дія впливу припинилась. З цією причини збурення руху частіше розглядають як вільний рух системи, оскільки простіше розв’язати однорідне диференціальне рівняння з ненульовими початковими умовами, ніж неоднорідне диференціальне рівняння з ненульовими початковими умовами.

Якщо незбурений рух характеризується функціями , збурений – функціями , то збурений рух можна описати відхиленням величин від тих значень, які вони мають при незбуреному русі:

Початковими умовами при вільному русі, що записаний у відхиленнях, будуть значення величин . Вони виникли в результаті дії збурення, що потім припинилась. Тому функції описують процес вільного руху в системі.

Як трактувати визначення стійкості в цьому випадку? Незбурений рух буде стійким, якщо для всякого додатного числа , яке б мале воно не було, можна підібрати інше число , яке залежить від , що для всіх незбурених рухів, для яких в початковий момент

, (4.1)

при всіх виконується нерівність

. (4.2)

З рівняння (4.2) випливає, що при оцінці стійкості відхилення не повинні перевищувати деякої достатньо малої величини , а з рівняння (4.1) – що початкові умови при цьому відрізняються від нуля, але не перевищують деяке значення , яке залежить від вибраного значення .

Якщо виконується умова , то система називається безмежно стійкою, тобто вона буде стійкою при будь-яких початкових відхиленнях. Якщо система стійка при і нестійка при , то вона є стійкою в малому і нестійкою у великому (при ). Якщо виконується умова , то система називається асиметрично стійкою.

Розглянемо, як можна математично оцінити стійкість лінійної автоматичної системи.

Вільний рух лінійної системи описують лінійним однорідним диференціальним рівнянням

(4.3)

з початковими умовами , де – порядок похідної.

Розв’язок цього рівняння являє собою суму членів

, (4.4)

де – корені характеристичного рівняння

, (4.5)

– постійні інтегрування, що залежать від початкових умов .

Щоби система була стійкою, рівняння (4.4) повинно задовольняти умову

. (4.6)

Корені характеристичного рівняння (4.5) в загальному випадку можуть бути суттєвими і комплексно спряженими. Нехай перших буде S, а других – n-S. Тоді розв’язок (4.4) можна представити у вигляді

. (4.7)

Розглянемо, як будуть змінюватись складові рівняння (4.7) при залежно від значення коренів. Якщо всі істотні корені від’ємні, то , так як кожна із складових при являє собою експоненту, що зменшується. Якщо істотні частини k всіх комплексних коренів від’ємні, то , оскільки кожен із складників являє собою затухаюче коливання. Таким чином, якщо в характеристичному рівнянні всі істотні частини комплексних коренів та прості корені від’ємні, то і система буде стійкою. Якщо хоча б один з істотних коренів або істотна частина пари комплексних коренів буде додатним, то відповідні їм складові в загальному розв’язку (4.7) і з часом будуть нескінченно зростати, і система буде нестійкою.

Таким чином, необхідною і достатньою умовою стійкості лінійної системи автоматичного керування є від’ємність істотних частин всіх коренів її характеристичного рівняння. Якщо істотна частина хоча б одного кореня дорівнює нулю, а істотні частини інших коренів – від’ємні, то система знаходиться на межі стійкості. За наявності кратних коренів з нульовими істотними частинами система буде нестійкою.

Отже, ми встановили необхідну і достатню умову стійкості лінійних автоматичних систем. Але майже всі реальні системи є нелінійними і тільки приблизно деякі з них можна описати лінійними рівняннями. Чи можна за стійкістю лінеаризованої системи судити про стійкість вихідної нелінійної системи? Це питання було вирішене А.М.Ляпуновим, який сформулював свої знамениті теореми про стійкість лінеаризованих систем. Ці теореми звучать так:

Якщо лінеаризована система стійка, то стійка і вихідна нелінійна система
Якщо лінеаризована система нестійка, то нестійка і вихідна нелінійна система
Якщо лінеаризована система знаходиться на межі стійкості, то для визначення стійкості вихідної нелінійної системи необхідно провести додаткові дослідження за вихідними нелінійними рівняннями системи.

Таким чином, теореми Ляпунова дозволяють стверджувати про стійкість нелінійної системи за лінійним рівнянням. І тільки в окремих випадках, коли аналіз лінійного рівняння покаже, що лінеаризована система знаходиться на межі стійкості, потрібні додаткові дослідження. Дійсно, автоматичні системи, що використовуються на практиці, повинні бути не тільки стійкими, але й мати певний запас стійкості, тобто повинні знаходитися на деякій відстані від межі стійкості. В противному разі при незначній зміні параметрів система може стати нестійкою і непридатною для подальшої роботи. Тому вузька зона, перехід якої переводить лінеаризовану систему із стійкої в нестійку, включає в себе також межу стійкості вихідної нелінійної системи.

Ми показали, що необхідною і достатньою умовою стійкості лінеаризованих, а отже, і вихідних нелінійних автоматичних систем, є від’ємність істотних частин всіх коренів їх характеристичних рівнянь. Отже, для визначення стійкості системи прийдеться вирішувати її характеристичні рівняння, щоби визначити знаки коренів останнього. Аналітичний розв’язок алгебраїчних рівнянь 3-го і 4-го порядків потребує багато часу, а рівняння 5-го і більш високих порядків аналітично взагалі не вирішуються.

Тому виникає запитання, як визначити знаки істотних частин коренів характеристичного рівняння, а отже, і визначити стійкість системи, не вирішуючи характеристичне рівняння.

Цим питанням займалось багато вчених. В результаті досліджень були сформульовані умови стійкості у вигляді так званих критеріїв стійкості. Перш за все було встановлено, що необхідною умовою стійкості системи є додатність всіх коефіцієнтів її характеристичного рівняння, для систем третього і більш високих порядків – є лише необхідною, але недостатньою умовою стійкості систем.

Які ж умови є не тільки необхідними, але й достатніми для стійкості системи? Які вихідні дані необхідні для визначення, чи виконуються ці умови?

Умови стійкості формулюються у вигляді різних критеріїв стійкості, кожен з яких використовують залежно від того, якими вихідними характеристиками і даними володіють. Якщо відомі диференціальні рівняння системи, то частіше використовують алгебраїчні критерії стійкості.

4.3 Алгебраїчні критерії стійкості

Перший алгебраїчний критерій, який можна використовувати для системи 3-го порядку, був сформульований І.А.Вишнеградським в 1876 р.:

для стійкості лінійної системи з характеристичним рівнянням

необхідне виконання двох умов:

всі коефіцієнти характеристичного рівняння повинні бути додатними;
похідна середніх коефіцієнтів повинна бути більша від похідної крайніх

В коефіцієнти рівнянь входять лише значення параметрів системи, тому стійкість останньої визначається тільки параметрами і не залежить від їх стану.

Для визначення систем будь-якого типу порядку використовують критерії Гурвіца та Рауса. Критерій Гурвіца більш простіший, тому його використовують частіше. Він формулюється так:

Система з характеристичним рівнянням

буде стійкою, якщо визначник і всі його діагональні мінори додатні:

При складанні визначника Гурвіца спочатку по діагоналі розміщують коефіцієнти, починаючи з до :

. (4.8)

Потім визначник заповнюють по стовпцях: вище діагональних коефіцієнтів записуються коефіцієнти із індексами, що зменшуються, а нижче – із зростаючими. При досягненні нульового або n-го індексу далі ставляться нулі.

Кожен діагональний мінор визначника Гурвіца отримують з попереднього мінору шляхом викреслювання нижнього рядка і правого стовпчика. Мінор отримують з визначника Гурвіца за загальним правилом, тобто шляхом викреслювання з нижнього рядка і правого стовпчика. Нижчий діагональний мінор Гурвіца .

Як приклад використаємо критерій Гурвіца для визначення стійкості системи з характеристичним рівнянням

Складемо визначник Гурвіца і його діагональні мінори

Звідси видно, що визначник Гурвіца і його діагональні мінори додатні. Отже, система, що досліджується, стійка.

Позитивною ознакою алгебраїчних критеріїв є простота використання, а недоліком – те, що вони не дозволяють оцінити вплив на стійкість системи параметрів окремих її елементів. Цього недоліку можна позбутися за допомогою графоаналітичного критерію А.В.Михайлова.

4.4 Графо-аналітичний критерій Михайлова

Представимо ліву частину рівняння

у вигляді функції від р

Зробивши заміну , отримаємо рівняння комплексного вектора

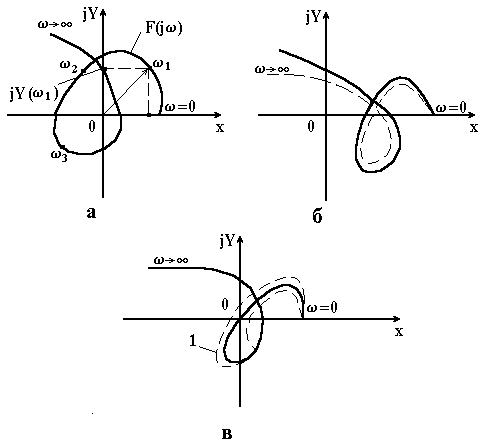
кінець якого при зміні від 0 до опише деяку криву – криву Михайлова. На рис. 4.1 показані криві Михайлова для систем 6-го порядку.

а – стійка система; б – система, що знаходиться на межі стійкості

Рисунок 4.1 – Криві Михайлова для систем шостого порядку

Розглянемо основні властивості кривої Михайлова. Крива Михайлова починається на дійсній осі при в точці і закінчується в n-ому квадранті (при ), якщо відлік квадрантів вести проти годинникової стрілки (n – порядок характеристичного рівняння). В n-ому квадранті крива Михайлова йде в нескінченність.

Щоб побудувати криву Михайлова, необхідно в функції замінити p на і розділити дійсну і уявну частини

Далі, задаючись різними значеннями необхідно знайти точки , , , ... За цими точками будують на комплексній площині криву Михайлова. Згідно з критерієм Михайлова лінійна система n-го порядку буде стійкою, якщо крива Михайлова охоплює початок координат і послідовно проходить n квадрантів.

Якщо крива Михайлова проходить через початок координат, то система може знаходитись на межі стійкості або бути нестійкою. Першому випадку відповідає така крива, яка при найменшій деформації в околі початку координат буде відповідати стійкій або нестійкій системі, а другому випадку – якщо деформація не призведе її до виду, який відповідає стійкій системі. На рис. 4.1 деформовані криві Михайлова показані пунктиром. Отже, для оцінки стійкості системи за допомогою критерію Михайлова важливо встановити розміщення кривої Михайлова, відносно початку координат.

Щоби за допомогою критерію Михайлова оцінити вплив зміни параметрів елементів системи на її стійкість, необхідно побудувати криву Михайлова при даному значенні параметра. Нехай, наприклад, вийшло так, що система знаходиться на межі стійкості (рис. 4.1, в). Потім слід змінити цей параметр, наприклад, збільшити і побудувати криву Михайлова для цього випадку (рис. 4.1, в, крива 1). З побудови випливає, що збільшення параметра, який нас цікавить, в зоні початкового його значення допомагає стійкості системи.

4.5 Частотні критерії стійкості

Для оцінки стійкості системи, замкнутої при відомій її АФЧХ, використовують частотний критерій Найквіста – Михайлова. Необхідна АФЧХ розімкнутої системи може бути отримана наступним чином.

Якщо є передавальна функція розімкнутої системи , де і – поліноми від p, то, замінивши р на j, отримаємо рівняння АФЧХ розімкнутої системи . Щоби побудувати АФЧХ, необхідно представити її такою, що складається з дійсної і уявної частин: .

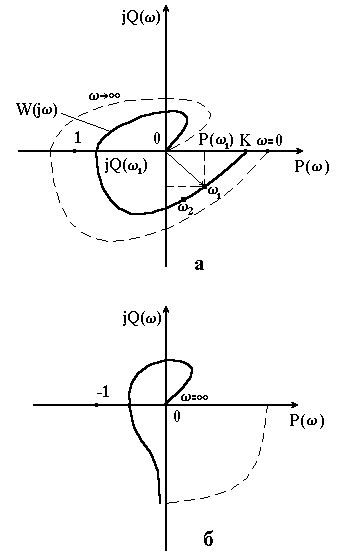
Потім, задаючись значеннями від 0 до : ; ; і т.д., необхідно знайти точки , , , ... і побудувати АФЧХ на комплексній площині (рис. 4.2, а).

Рисунок 4.2 – АФЧХ стійкої (а) і що знаходиться на межі стійкості (б) розімкнутих систем, які будуть стійкими в замкнутому стані

Розглянемо основні властивості АФЧХ розімкненої системи. Якщо розімкнена система не має інтегруючих ланок, то при її АФЧХ починається на дійсній осі в точці , де К – коефіцієнт підсилення розімкнутої системи. Закінчується АФЧХ при на початку координат (рис. 4.2, б).

Важливо відзначити, що розімкнена система може бути стійкою, нестійкою або знаходитись на межі стійкості. Якщо система складається тільки зі стійких елементів, то вона буде стійкою в розімкнутому стані. За наявності хоча б одного нестійкого елемента вона буде нестійкою. За наявності однієї інтегруючої ланки розімкнута система знаходиться на межі стійкості (в літературі такі системи інколи називають нейтрально-стійкими).

Сформулюємо тепер критерій Найквіста-Михайлова (частковим критерій стійкості називають завдяки тому, що він був розроблений Найквістом для дослідження підсилювачів із зворотним зв’язком, а Михайлов узагальнив цей критерій для дослідження стійкості замкнутих автоматичних систем):

якщо розімкнута система стійка або знаходиться на межі стійкості, то для того, щоб замкнута система була стійка, необхідно і достатньо, щоби амплітудно-фазова частотна характеристика розімкненої системи при зміні від 0 до не охоплювала точку з координатами {–1, j0}. Якщо розімкнена система нестійка, а її передавальна функція має m полюсів справа від уявної осі площини р, то для стійкості замкнутої системи необхідно і достатньо, щоби АФЧХ розімкнутої системи при зміні від - до + охоплювала точку {–1, j0} m разів.

Як визначити, чи охоплює АФЧХ розімкнутої системи точку , якщо розімкнута система знаходиться на межі стійкості, бо АФЧХ при прямує до нескінченності. В цьому випадку уявно з’єднують кінець АФЧХ при з додатною дійсною піввіссю другого кола, нескінченно великого радіуса (рис. 4.2 , б). Тоді можна однозначно визначити, чи охоплює АФЧХ точку .

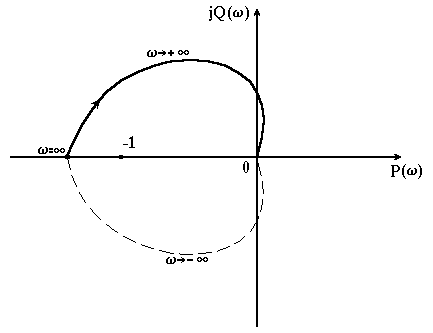
Чому у випадку стійкості розімкненої системи розглядається АФЧХ при зміні від 0 до , а у випадку нестійкої – при зміні від - до +? На практиці АФЧХ може бути знята тільки для додатних частот (). З математичної точки зору АФЧХ повинні будуватись для всього діапазону частот – , при цьому гілка АФЧХ для від’ємних частот симетрична відносно дійсної осі гілки, побудованої для додатних частот, якщо ця гілка не охоплює або охоплює точку m разів. Якщо ж розглядати тільки додатну ланку (гілку), то вона повинна охоплювати цю точку разів. Наприклад, при вона повинна охоплювати її разу. Але таке визначення доволі невдале. Тому при нестійкій розімкненій системі розглядають дві гілки її АФЧХ, тобто беруть діапазон зміни частоти від - до + (рис. 4.3). Звідси видно, що при використанні частотного критерію стійкості визначним є положення АФЧХ розімкненої системи поблизу точки .

Рисунок 4.3 – АФЧХ нестійкої розімкнутої системи (m=1), яка буде стійкою

в замкнутому стані

За допомогою критерію Найквіста-Михайлова, як і критерію стійкості Михайлова, можна оцінити вплив параметрів елементів системи на її стійкість. Для цього необхідно побудувати АФЧХ розімкнутої системи при даному значенні параметра і визначити стійкість замкнутої системи. Нехай для прикладу система є стійкою (рис. 4.4). Змінимо значення цього параметра. Нехай при новому значенні параметра (наприклад, при більшому) АФЧХ набула вигляду, зображеного на рис. 4.4 пунктиром. Отже, збільшення параметра спонукає нестійкості системи.

Рисунок 4.4 – АФЧХ стійкої розімкнутої системи

Так як критерій Найквіста-Михайлова використовує експериментально зняті АФЧХ, то неважко дати його фізичну трактовку. Пояснимо це спочатку на прикладі системи, яка знаходиться на межі стійкості. В цьому випадку АФЧХ розімкненої системи при деякій частоті проходить через точку (рис. 4.4). Це означає, що при даній частоті амплітуда вихідного сигналу дорівнює амплітуді вхідного сигналу, а його фаза прямо протилежна фазі вхідного сигналу, тобто зсув по фазі між ними дорівнює -. При замиканні системи основний зворотний зв’язок повинен бути від’ємний, тобто фазу вихідного сигналу при подачі його на вхід системи слід повернути на . Крім того, при цьому слід відключити зовнішнє джерело коливань, яке подавало гармонійні сигнали на вхід системи.

Отже, при замиканні системи вихідний сигнал (правда, тепер він вже не буде вихідним, оскільки він поданий на вхід системи, але ми знову для якості будемо його називати вихідним) буде співпадати за амплітудою і фазою з вхідним сигналом, тобто при замиканні системи в ній нічого не зміниться. В системі встановляться незатухаючі коливання, причому вони будуть підтримуватись не за рахунок енергії джерела вхідного сигналу (воно тепер відключене), а за рахунок енергії самої системи. Це і означає знаходження системи на межі стійкості.

Якщо АФЧХ при частоті перетинає дійсну вісь зліва від точки , то вона охоплює дану точку. Це свідчить про те, що в розімкнутій системі амплітуда вихідного сигналу на даній частоті більша від амплітуди вхідного сигналу, а зсув по фазі між ними дорівнює -. При замиканні системи і відключенні джерела зовнішніх коливань амплітуда вихідних коливань буде зростати, тобто система буде нестійкою. Якщо АФЧХ не охоплює точки , то при зсуві по фазі, рівному -, амплітуда вихідного сигналу менша, ніж амплітуда вхідного сигналу. В цьому випадку при замиканні системи коливання в ній будуть затухати, тобто система буде стійкою.

Тепер розглянемо, як використати частотний критерій стійкості Найквіста-Михайлова, якщо в розпорядженні є не АФЧХ, а ЛАЧХ розімкненої системи. Сформулюємо даний критерій для даного випадку.

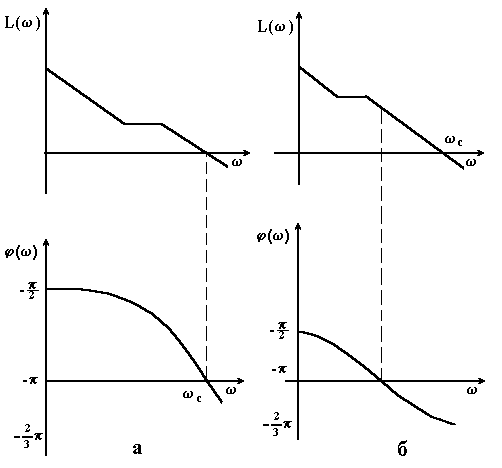
Замкнута мінімально фазова система стійка, якщо при досягненні фазової частотною характеристикою значення - логарифмічна амплітудно-частотна характеристика буде від’ємною (рис. 4.5). До мінімально-фазових систем відносяться такі, порядок числівника передавальної функції яких нижчий порядку знаменника і відсутні нулі передавальної функції (корені рівняння ) в правій півплощині р.

Чому розглядається ЛАЧХ при значенні фази, рівному
-? Тому що стійкість згідно з критерієм Найквіста-Михайлова оцінюється тим, з якого боку від точки АФЧХ перетинає дійсну вісь комплексної площини, а при перетині дійсної осі фаза АФЧХ дорівнює -.

Якщо ЛАЧХ від’ємна, то модуль АФЧХ менший одиниці, оскільки числа, менші одиниці, мають від’ємні логарифми. Від’ємність ЛАЧХ при фазі - свідчить про те, що АФЧХ розімкнутої системи не охоплює точку .

Чому при оцінці стійкості системи за ЛАЧХ вважається, що критерій Найквіста-Михайлова можна використовувати тільки для мінімально-фазових систем, адже при використанні АФЧХ такого обмеження не було? Це пояснюється тим, що при оцінці стійкості за ЛАЧХ розглядається тільки частина її при фазі, близькій до -, або частина АФЧХ в околі перетину нею дійсної осі. Тільки для мінімально-фазових систем розгляд частини АФЧХ (ЛАЧХ) свідчить про всю характеристику. Для немінімально-фазових систем це зробити неможливо.

Всі розглянуті критерії стійкості тим або іншим способом оцінюють один і той же факт: чи є серед коренів характеристичного рівняння замкнутої системи корені з додатною дійсною частиною. Тому всі вони дають однаковий результат в оцінці стійкості системи.

Відзначимо, що у всіх випадках перш ніж досліджувати стійкість за допомогою того чи іншого критерію, слід впевнитись, що необхідна умова стійкості виконується, тобто всі коефіцієнти характеристичного рівняння системи є додатними числами.

4.6 Оцінка стійкості автоматичної системи за її структурою

В ряді випадків оцінити стійкість автоматичної системи можна за її структурою. Це значно скорочує час, так як немає необхідності складати характеристичне рівняння.

Якщо система має таку структуру, що в ній неможливо забезпечити стійкість ні при якому значенні параметрів її елементів, то така система називається структурно-нестійкою.

Оцінимо стійкість даної системи за її структурою. Наприклад, якщо система має дві інтегруючих ланки, неохоплені жорстким зворотним зв’язком, і не має послідовно включених диференціюючих ланок, то вона буде нестійкою при будь-якому значенні параметрів її елементів.

Покажемо це на прикладі простішої системи, яка складається з однієї аперіодичної і двох інтегруючих ланок. Передавальна функція такої системи в розімкнутому стані

а характеристичне рівняння замкнутої системи

Для цього рівняння не виконується необхідна умова стійкості. Отже, система буде нестійка при будь-яких значеннях параметрів Т і К, тобто вона буде структурно нестійкою. Структурно нестійку систему можна перетворити в стійку тільки заміною її структури, тобто введенням додаткових елементів, наприклад диференціюючих елементів при включенні пропорційних елементів паралельно інтегруючим.

Рисунок 4.5 – ЛАЧХ нейтральної (а) і нестійкої (б) розімкнутих систем
в замкнутому стані

4.7 Синтез систем автоматичного керування, виходячи з умов стійкості

При синтезі системи автоматичного керування виникає задача вибору таких значень параметрів її елементів, при яких система буде стійкою. Щоби здійснити такий вибір, слід підставити значення параметрів, що нас цікавлять, в характеристичне рівняння системи або в передавальну функцію в загальному вигляді, тобто у вигляді літер.

Далі слід використати вибраний критерій, тобто записати умови, при яких система буде стійка. В результаті отримаємо ряд рівнянь або нерівностей, з яких визначимо значення параметрів. Нехай характеристичне рівняння системи має вигляд

Потрібно визначити значення постійної часу Т, при яких система буде стійкою.

Використаємо критерій Вишнеградського, отримаємо три нерівності

; (4.9)

; (4.10)

. (4.11)

З нерівності (4.11) знайдемо . При цьому значенні Т нерівності (4.9) і (4.10) також виконуються. Отже, при будь-яких система буде стійкою.

Як можна спростити розв’язок задачі синтезу, виходячи з умов стійкості? Для цього необхідно знати, які фактори викликають нестійкість системи. Одним з найважливіших факторів є великий коефіцієнт підсилення розімкненої системи. В цьому легко впевнитись, використовуючи, наприклад, критерій Найквіста-Михайлова.

Нехай передавальна функція розімкнутої системи має вигляд , де і – поліноми від р, вільні члени яких рівні одиниці; К – коефіцієнт підсилення розімкнутої системи.

АФЧХ розімкнутої системи, отриманої з передавальної функції заміною р на j , має вигляд

Збільшення коефіцієнта підсилення К збільшує модуль АФЧХ, тому точка перетину АФЧХ з дійсною віссю переміщується вліво, і система в кінці кінців може перетворитись зі стійкої в нестійку (рис. 4.2, а).

Як це пояснити з фізичної точки зору? При великому коефіцієнті підсилення вихідний сигнал розімкнутої системи, що при замиканні подається на вхід системи, значно переважає попередньо поданий вхідний сигнал. Система підсилює цей сигнал, і він знову подається на вхід. Процес наростає лавиноподібно, і система швидко виходить з початкового встановленого стану.

Завдання синтезу систем значно полегшується, якщо побудувати області стійкості в площині тих параметрів, які необхідно вибрати. Побудова областей стійкості особливо зручна, якщо число варійованих параметрів рівне двом. Області стійкості включають в себе ті значення шуканих параметрів, при яких синтезована система буде стійкою.

Визначення межі областей стійкості для двох параметрів проводиться принципово так само, як і при виборі одного параметра, який ми розглянули вище.

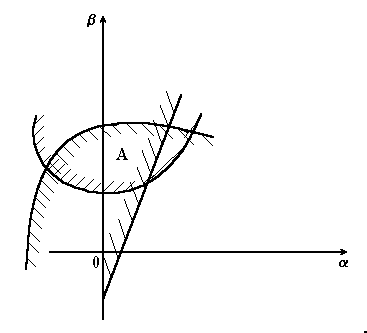
Для цього в характеристичному рівнянні або в передавальній функції системи ті параметри, що нас цікавлять, записують в загальному вигляді, тобто у вигляді літер. Потім на основі вибраного критерію записують умови знаходження системи на межі стійкості. З цією метою нерівності записують у вигляді рівнянь. Використання нерівностей в подальшому дозволить відрізнити області стійкості від областей нестійкості. На основі рівнянь будують криві або прямі в площині параметрів. Ці криві штрихують так, щоби штриховка була направлена в той бік півплощини, точки якої задовольняють даній умові стійкості. Областями стійкості будуть ті області, штриховка меж яких направлена в один бік (область А на рис. 4.6).

Рисунок 4.6 – До визначення області стійкості в площині параметрів: і

Для прикладу побудуємо області стійкості в площині параметрів Т і К для системи, характеристичне рівняння якої

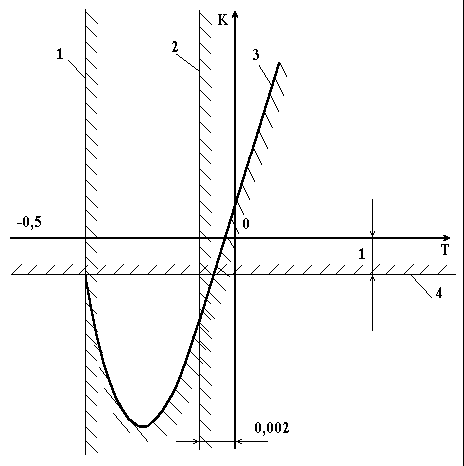
Граничні криві будуть мати вигляд (на рис. 4.7, криві відповідно 2, 1, 4 і 3)

; (4.12)

; (4.13)

; (4.14)

, (4.15)

а умови стійкості – відповідно

Рисунок 4.7 – До визначення меж області стійкості в площині параметрів Т і К

З рис. 4.7. видно, що областю стійкості буде частина площини К, Т, яка розміщена в першому квадранті і йде від граничної прямої 4 вверх, а від граничної кривої 3 – вправо.

Принципово такими ж будуть межі областей стійкості при використанні інших критеріїв стійкості. Слід зазначити, що побудова областей стійкості в площині параметрів значно простіша при використанні алгебраїчних критеріїв та критерію Михайлова, ніж при використанні частотних критеріїв.

Дуже важливо визначити, які значення параметрів системи доцільно вибирати, якщо в розпорядженні є області стійкості, побудовані в площині цих параметрів. На перший погляд здається, що значення параметрів можуть бути будь-якими, лиш би вони належали області стійкості. Але це не так. Якщо взяти значення параметрів, близькі до межі області стійкості, то на практиці може статись, що в результаті звичайної неточності виготовлення системи або в результаті зміни параметрів в процесі експлуатації їх значення можуть бути такими, що не відповідатимуть області стійкості системи. Система стане нестійкою і, отже, непридатною до експлуатації.

Щоби усунути можливість виникнення нестійкості системи, вводять запас її стійкості.

4.8 Запас стійкості автоматичної системи

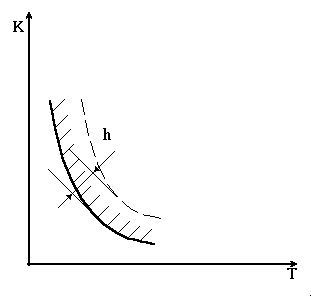
Запас стійкості – це кількісна оцінка відстані значень параметрів системи або її характеристик від зони, небезпечної з точки зору стійкості. Запас стійкості по параметрах характеризує відстань граничної кривої, яка визначає область вирішених значень параметрів, від межі області стійкості. На рис. 4.8 запас стійкості по параметрах Т і К позначений через h.

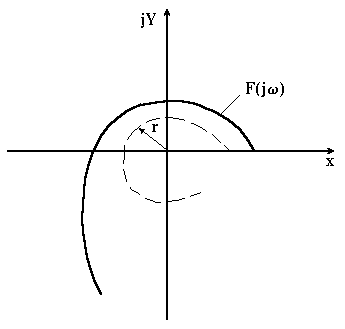
Запас стійкості за критерієм Михайлова дорівнює радіусу кола r, в яке не повинна заходити крива Михайлова (рис. 4.9). Центром кола є “небезпечна” точка при використанні критерію Михайлова, тобто початок координат площини F.

При використанні критерію Найквіста-Михайлова “не-безпечною” точкою є точка з координатами . Оцінка запасу стійкості, виходячи з цього критерію, проводиться за амплітудою і за фазою.

Рисунок 4.8 – Запас стійкості по параметрах Т і К

Рисунок 4.9 – Запас стійкості при використанні критерію Михайлова

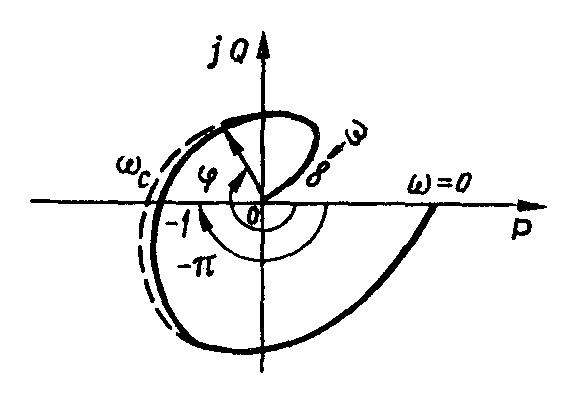
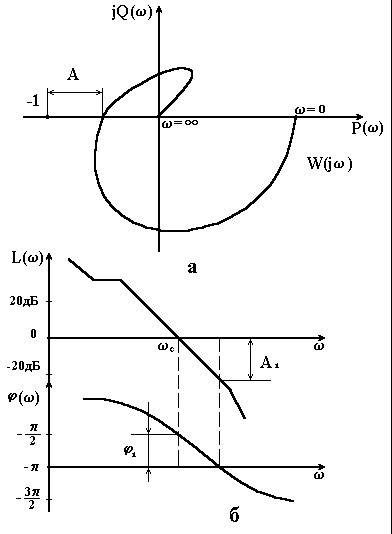
Запас стійкості по амплітуді А (рис. 4.10, а) дорівнює відстані від точки перетину АФЧХ розімкненої системи дійсної осі до точки , а запас по фазі 1 (рис. 4.10, а) – куту між дійсною віссю і вектором, проведеним з початку координат в точку перетину АФЧХ з колом одиничного радіуса.

При оцінці стійкості за логарифмічними частотними характеристиками запас стійкості по амплітуді визначається як ордината ЛАЧХ при фазі і вимірюється в децибелах. Запас стійкості по фазі визначається за фазовою частотною характеристикою при частоті зрізу , тобто при частоті перетину ЛАЧХ осі частот. В цій точці значення ЛАЧХ рівне нулю, так як модуль АФЧХ в цій точці дорівнює одиниці.

На рис. 4.10, б запас по амплітуді виражений в логарифмічному масштабі. Чи більше за абсолютною величиною , тим дальше від точки –1 перетинає АФЧХ стійкої системи дійсну вісь і, отже, тим більша величина А (рис. 4.10, а). Звідси випливає, що запаси по амплітудах А і однаково характеризують розміщення АФЧХ розімкненої системи при фазі
–, тільки вимірюються вони в різних масштабах.

У випадку, коли побудовані межі області стійкості в площині параметрів системи, запас стійкості слід виразити як деяке умовне поширення h від цих меж (рис. 4.8). Найчастіше ці нові межі проводять еквідистантно (на однаковій відстані) від теоретично розрахованої межі стійкості. Ступінь видалення гарантованої області стійкості від розрахованої називають запасом стійкості за параметром, на відміну від попередніх випадків, де розглядався запас стійкості за показником вибраного критерію. Незалежно від прийнятої форми запас стійкості є кількісною характеристикою, і використання його при розрахунках є гарантією стійкості системи в реальних умовах.

Висновки. Дослідження стійкості є одним з перших етапів оцінки систем автоматичного управління при їх аналізі. Проводячи аналіз або синтез автоматичної системи, необхідно впевнитись в тому, що система структурно стійка.

Рисунок 4.10 – До визначення запасу стійкості за фазою і за амплітудою за допомогою АФЧХ (а) та ЛАЧХ і ФЧХ (б) розімкненої системи

Якщо розв’язується задача аналізу, то оцінка стійкості проводиться за допомогою одного з розглянутих критеріїв. За наявності диференціального рівняння замкнутої системи потрібно використовувати алгебраїчні або графоаналітичні критерії стійкості: при третьому порядку рівняння – критерій Вишнеградського, при четвертому і п’ятому – критерій Гурвіца, а при більш високому порядку – критерій Михайлова. За наявності частотних характеристик оцінку стійкості потрібно проводити за допомогою частотних критеріїв. Якщо розв’я-зується задача синтезу, виходячи з умов стійкості, і при цьому визначається значення параметрів системи, то потрібно використати алгебраїчні критерії або критерії Михайлова і попередньо побудувати межі області стійкості в площині варійованих параметрів.

На практиці вибір прикладів систем переважно проводять, виходячи не тільки з умов стійкості, але й з умов забезпечення потрібної якості перехідного процесу. В цьому випадку ефективними є логарифмічні частотні характеристики систем.

4.9 Показники якості перехідних процесів

З попередніх тверджень ми знаємо, що автоматична система передусім має бути стійкою. В стійкій системі перехідний процес затухає. Однак для практики не є байдужим характер затухання перехідного процесу. Так, наприклад, якщо перехідний процес затухає помалу, і система довго входить в новий установлений режим, то вона володіє недостатньою швидкодією, і, як наслідок, її застосування буде обмеженою. Тому стійкість є необхідною але недостатньою умовою роботоздатності автоматичних систем. Достатньою умовою є якість процесів і помилками в установлених режимах.

Якість перехідних процесів здебільшого оцінюють за перехідною функцією , яка являє собою реакцію на зовнішній вплив типу одиничної ступінчатої функції . Для слідкуючих систем керування розглядають перехідну функцію по відношенню до заданого впливу , а для систем стабілізації – по відношенню до .

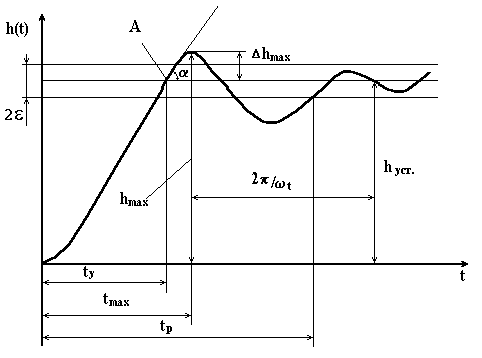
На прикладі перехідної функції (рис. 4.11) ознайомимось з основними показниками якості перехідного процесу: часом коливань, перерегулюванням, основною частотою коливань, кількістю коливань, максимальною швидкістю і максимальним прискоренням регульованої величини.

Рисунок 4.11 – Графік перехідної функції h(t)

Час регулювання визначається тривалістю перехідного процесу. Теоретично перехідний процес триває нескінченно довго, однак на практиці вважається, що він закінчується, як тільки відхилення керованої величини від нового її встановленого значення не буде перевищувати допустимих значень . Найчастіше приймається від . Часом регулювання характеризують також часом досягнення перехідною функцією перший раз нового встановленого значення або часом досягнення максимального значення .

Перерегулювання , або вихід, являє собою максимальне відхилення регульованої величини від нового значення, що встановилося. Як правило, перший максимум є найбільшим. Відносне перерегулювання вираховується за формулою

Час регулювання і перерегулювання, основні показники перехідного процесу, тісно пов’язані між собою. На перший погляд може здатися, що перерегулювання недопустиме, так як воно збільшує час регулювання. Однак це не так. Переважно перерегулювання появляється внаслідок того, що система до нового встановленого стану підходить з певною швидкістю, яка графічно відображається тангенсом кута нахилу дотичної в точці А (рис. 4.11).

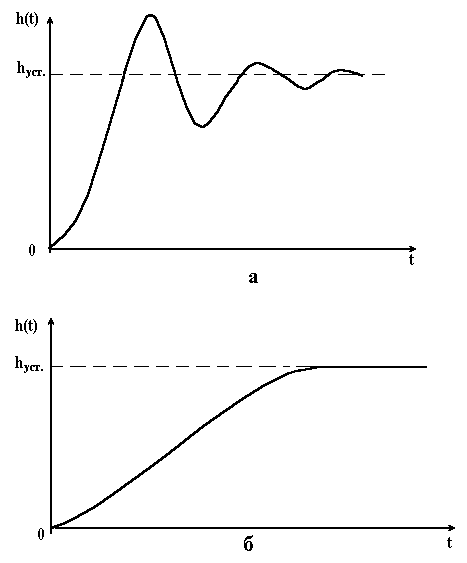
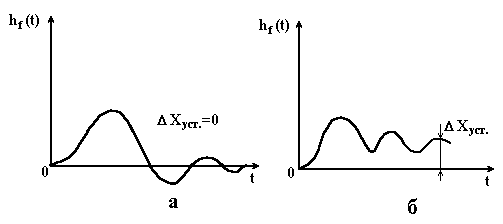
Чим більша ця швидкість, тим довше за встановлене положення пройде система за інерцією. Отже, для зменшення перерегулювання необхідно зменшити швидкість, з якою система підходить до нового встановленого стану. Це, в кінці кінців, призводить до збільшення часу регулювання. Якщо система підходить до нового встановленого стану з нульовою швидкістю, то перерегулювання зовсім не буде, але час регулювання значно збільшиться (рис. 4.12, б).

Так як час регулювання характеризує швидкодію системи, то стараються, там, де це необхідно, звести її до мінімуму. Це означає, що система має відробляти задану дію з великою швидкістю, що в подальшому призводить до великого перерегулювання. Крім цього, оскільки перехідний процес коливається, то будуть мати місце великі прискорення регульованої величини, що може викликати недопустимо великі динамічні навантаження на елементи системи. Таким чином, як відсутність, так і дуже велике перерегулювання небажані. Тому як оптимальне допускають перерегулювання в межах 20-30%. При цьому число напівколивань перехідної функції рівне 2-3.

Числові значення регулювання перерегулювання часто задаються як вихідні дані синтезу коректуючих механізмів, оскільки забезпечується подавлення небажаних відхилень регульованої величини в перехідному процесі.

Рисунок 4.12 – Графіки перехідних функцій з великим перерегулюванням в системі (а) та при відсуності перерегулювання (б)

Для деяких систем перерегулювання зовсім небажане, наприклад, для систем автоматичного регулювання хімічних процесів, де перерегулювання може погіршити продукцію, що виготовляється. Необхідно також мати на увазі, що бажання зменшити час регулювання призведе до збільшення потужності виконуючого пристрою.

4.10 Методи побудови перехідних процесів

Для визначення числових значень показників перехідного процесу необхідно мати його криву, яку можна отримати трьома різними способами: експериментально, за допомогою моделювання та розрахунковим шляхом. Проведемо огляд розрахункових методів встановлення і побудови перехідних процесів. До них відносяться методи, що грунтуються на роз-в’язанні диференціальних рівнянь та частотний метод.

Спочатку розглянемо встановлення перехідної функції шляхом розв’язання диференціальних рівнянь системи.

Відомі методи розв’язку диференціальних рівнянь розділяють на точні і наближені. До точних відносяться класичні і операційні методи. Різні чисельні та графічні методи роз-в’язку диференціальних рівнянь є наближеними.

При розв’язанні диференціальних рівнянь класичним методом виникають труднощі, пов’язані з розв’язанням характеристичного рівняння для знаходження його коренів, та з розв’язанням системи алгебраїчних рівнянь для знаходження сталих інтегрування з початкових даних. Ці труднощі збільшуються із збільшенням порядку диференціального рівняння. Крім того розв’язання диференціального рівняння значно ускладнюється, якщо початкові значення не нульові, а права частина рівняння містить похідні.

Тому класичний спосіб в автоматиці знаходить обмежене застосування, інколи використовується для рівнянь другого і третього порядку.

Розв’язання диференціальних рівнянь операційним методом зводиться до відшукання оригіналу функції за відомим її зображенням шляхом зворотного перетворення Лапласа. Так, якщо ми хочемо знайти перехідну функцію , то необхідно знати її зображення

Зображення легко знайти за допомогою передавальної функції замкнутої системи . Дійсно,

Якщо прийняти , то і, враховуючи, що зображення одиничної ступінчатої функції рівне , отримаємо

. (4.16)

Тоді

Для пошуку оригіналу можна скористатися таблицями зображень. Це, наприклад, вигідно робити при визначенні перехідних функцій типових ланок, так як в таблицях приведені прості вирази для зображень.

Зображення для автоматичних систем є завжди складною функцією аргументу р. В цьому випадку для знаходження оригіналу можна користуватися теоремою розкладу. Ця теорема – для випадку, коли зображення може бути показано у вигляді

, (4.17)

тобто має один нульовий корінь в знаменнику, і виражається формулою

, (4.18)

де – корені рівняння ; ; n – степінь полінома . Операційний метод розв’язання диференціальних рівнянь порівняно з класичним має ту перевагу, що в ній залишається тільки одна складна операція – знаходження коренів алгебраїчного рівняння . Друга операція, пов’язана зі знаходженням вільних сталих інтегрування, відпадає, оскільки початкові умови (нульові) враховуються автоматично при складанні передавальної функції системи. Тому операційний метод є більш зручним і його часто застосовують для вирішення практичних завдань автоматичного регулювання.

Для побудови кривої перехідного процесу можуть бути використані числові і графоаналітичні методи розв’язання диференціальних рівнянь.

Частотний метод побудови перехідного процесу

Побудова кривої перехідного процесу для відомих частотних характеристик системи має велике практичне значення, так як це не пов’язано з великими розрахунками, особливо при застосуванні логарифмічних частотних характеристик. Крім того, частотні характеристики можна зняти експериментально.

Частотний метод побудови перехідного процесу грунтується на кількісному зв’язку між тимчасовими і частотними характеристиками, що відображається перетворенням (інтегралом) Фур’є

, (4.19)

причому

, (4.20)

де – зображення Фур’є функції .

Як функцію часу будемо розглядати перехідну функцію . Тоді отримаємо

, (4.21)

де

Функція є амплітудно-фазовою характеристикою замкнутої системи.

Таким чином, зв’язок між перехідною функцією і частотною характеристикою має вигляд

. (4.22)

Отриманою формулою при розрахунках користуватись незручно через наявність комплексних функцій під знаком інтегралу. Тому, враховуючи відомі співвідношення

формулу (4.22) можна привести до вигляду

, (4.23)

або

, (4.24)

де і – відповідно дійсно і уявна частотні характеристики замкнутої системи.

Таким чином, за формулами (4.23) або (4.24) можна розрахувати перехідну функцію і побудувати її графік, якщо відома частотна характеристика або . Але, оскільки функції і є складними дрібно-раціональними, то інтеграли в формулах (4.23) і (4.24) важко вираховуються. Ці важкості можна обминути, якщо отримати функції і у вигляді графіків, що, як було показано в шостій частині, можна зробити досить простими способами. Тому виникло завдання побудови перехідної функції за відомим графіком або . Це завдання було вирішено професором В.В.Солодовниковим, який запропонував наближений графоаналітичний метод побудови перехідного процесу.

Суть даного методу полягає в тому, що графік розбивають на типові трапеції. Потім для кожної трапеції на основі попередньо складених таблиць h–функцій, розрахованих за допомогою формули (4.23), будують графік перехідної функції. Шукану перехідну функцію знаходять шляхом алгебраїчного додавання ординат окремих складових.

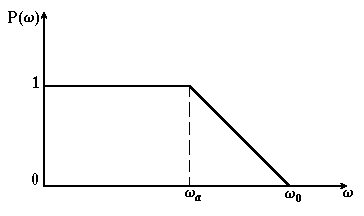
Таблиці h–функцій складені для одиничної трапеції, яка характеризується коефіцієнтом нахилу (рис. 4.13). Така таблиця дозволяє для заданого значення побудувати графік перехідної відносного часу , де t – поточний час перехідного процесу. Якщо висота трапеції не дорівнює одиниці, то графік відповідно змінить свій масштаб по осі ординат.

Рисунок 4.13 – Типова одинична трапецеїдальна дійсна частотна характеристика

Побудова перехідної функції автоматичної системи за методом проф. В.В.Солодовникова зручно робити в такій послідовності:

Знаходять передавальну функцію розірваної системи (за відповідним диференціальному рівнянням або за структурною схемою системи).
За передавальною функцією будують логарифмічну амплітудну і фазову частотні характеристики.
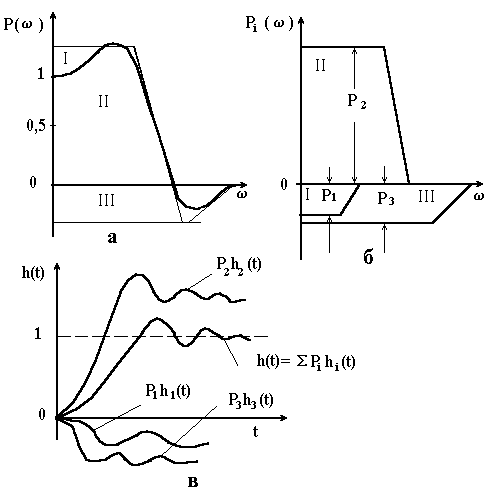
За значеннями і за допомогою р-номо-грами визначають значення і будують графік речової частотної характеристики замкнутої системи (рис. 4.14, а).

Рисунок 4.14 – До побудови дійсної частотної характеристики на основі трапецеїдальної і вдповідні їм перехідні процеси

Графік розбивають на типові трапеції І, ІІ і ІІІ для кожної з яких визначають її параметри , і (рис. 4.14, б).
Для кожної з цих трапецій за допомогою таблиці h–функцій будують графік ; при цьому відносний час перераховують в реальний (рис. 4.14, в).
Шукану перехідну функцію знаходять шляхом алгебраїчного додавання ординат перехідних функцій, що відповідають кожній трапеції (рис. 4.14, в).

Точність методу повністю достатня для інженерних розрахунків і в значній степені залежить від точності апроксимації графіка Р() трапеціями.

Таблиця 4.1 – Типові ЛАЧХ розімкнутих систем

Тип ЛАЧХ	Передавальна функція	Нахили послідовних ділянок дБ/дек
І		-20, -40, -20, -40
ІІ		-20, -60, -20, -40
ІІІ		-20, -40, -20, -60
ІV		-20, -60, -20, -60

4.11 Непрямі оцінки якості перехідних процесів

Всесторонню оцінку якості неперехідного процесу роблять за графіком перехідної функції, вирахування і побудова якого є доволі складним і громіздким завданням. У зв'язку з цим виникає питання: чи потрібно знати всі деталі перехідного процесу? Насправді, для вирішення практичних завдань зовсім не обов’язкове точне дотримання певної визначеної форми перехідної функції, тому не потрібно знати і всі прямі показники якості. Таким чином, побудувавши з деякими труднощами графік перехідної функції, отримаємо значно більше, ніж потрібно, даних для розрахунків в техніці автоматичного керування. Тому при дослідженні якості керування не завжди необхідно будувати криву перехідного процесу. Така постановка завдання призводить до знаходження непрямих методів оцінки перехідного процесу.

Непрямими оцінками називають деякі числа, що характеризують окремі сторони перехідного процесу. Ці числа можна знайти порівняно простими способами без побудови графіка перехідного процесу. Значення непрямих оцінок полягає в тому, що вони дозволяють в деякій мірі стверджувати про вплив параметрів системи на її динамічні властивості.

Існує декілька непрямих оцінок якості перехідного процесу: оцінка за частотними характеристиками, інтегральні оцінки, кореневі методи і т.д. Ознайомимося з деякими з цих оцінок, що найбільш часто застосовуються на практиці. Перш за все розглянемо, як можна оцінити перехідний процес за частотними характеристиками замкнутої системи.

Припустимо, що вихідний сигнал слідкуючої системи в будь-який момент часу точно копіює вхідний. Тоді ж передавальна функція замкнутої системи і відповідна амплітудна фазова характеристика також дорівнює одиниці: . Отже, амплітудно-частотна і фазово-частотна характеристики відповідно будуть рівні

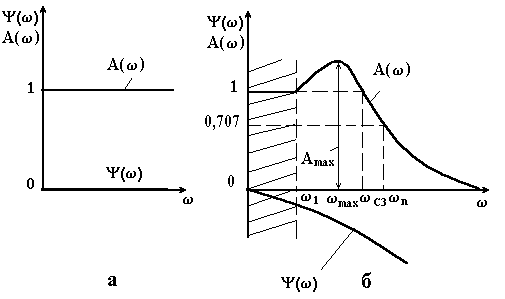
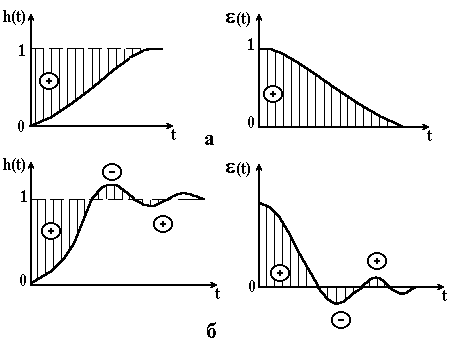
Іншими словами, на всіх частотних примусових коливаннях амплітуда вихідного сигналу дорівнює амплітуді вхідного, і зсув фаз між ними дорівнює нулю (рис. 4.15, а). Але рівність може виконуватися тільки в ідеальному випадку – якщо всі елементи системи безінерційні. Тому внаслідок інерційності системи, яка відбивається постійними часу її ланок, амплітудна і фазова частотні характеристики замкнутої системи переважно мають вигляд, приведений на (рис. 4.15, б). В цьому випадку умови і виконуються на невеликій ділянці малих частот (заштрихована ділянка на рис. 4.15, б). На резонансній частоті амплітудна характеристика має максимум . При подальшому збільшенні частоти система внаслідок своєї інерційності не встигає реагувати на коливання великих частот, і різко падає. Фазова частотна характеристика від’ємна. Отже, вихідний сигнал відстає по фазі від вхідного. За своїми частотними властивостями слідкуюча система може бути віднесена до класу фільтрів нижніх частот, які добре пропускають коливання малих частот і погано – великих.

Рисунок 4.15 – Амплітудна і фазова частотні характеристики ідеальної (а) і реальної (б) слікуючих систем

Встановлено, що чим більша , тим більш коливальний є перехідний процес. Тому співвідношення називають показником коливання. Для слідкуючих систем , тому . Часто . При малих М система “в’яла” і має більший час регулювання. При великих М збільшується перерегулювання, і система наближується до межі стійкості.

Крім частоти , характерними частотами амплітудно-частотної характеристики є і . Частота називається частотою зрізу замкнутої системи і визначається на рівні . Для слідкуючих систем частота визначає діапазон частот вимушених коливань, які пропускає система без послаблення. На цій частоті амплітуди вхідного і вихідного коливань рівні між собою. Частота називається смугою пропускання замкнутої системи і визначається на рівні Та як в діапазоні частот амплітудна характеристика різко падає, то цифрові значення частот і близькі один до одного.

Смуга пропускання впливає на точність і швидкодію системи. Із збільшенням смуги пропускання швидкодія системи збільшується. Чим більша смуга пропускання, тим більший спектр вхідного сигналу передається системою без викривлення. Отже, точність обробки вхідного сигналу підвищується. Але за наявності високочастотних перешкод у вихідному сигналі нереально розширювати смугу пропускання, так як при цьому система буде однаково добре пропускати як корисний сигнал, так і перешкоди.

Таким чином, показник коливальності М і смуга пропускання (частота зрізу ) замкнутої системи є непрямими показниками якості перехідного процесу, і їх необхідні значення можуть служити вихідними даними при проектуванні автоматичних систем.

При аналізі і синтезі автоматичних систем часто використовують логарифмічні амплітудні частотні характеристики (ЛАЧХ) розімкнених систем. Як нам уже відомо, за цими характеристиками судять про стійкість системи. Але, що ще важливіше, за ними можна судити про якість регулювання. Більше того, якщо для дослідження стійкості необхідно мати дві характеристики – амплітудну і фазову, то про якість регулювання можна судити тільки за однією амплітудною характеристикою. Така оцінка можлива для мінімально-фазових систем.

На основі розрахунків перехідних процесів було встановлено, що для позитивної якості регулювання ділянка середніх частот () ЛАЧХ повинна мати схил, що дорівнює –20 дБ/дек (рис. 4.7). Протяжність цієї ділянки впливає на перерегулювання, в тому числі з його збільшенням зменшується коливальність перехідного процесу. Прийнята якість перехідних процесів має місце, якщо протяжність цієї ділянки приблизно дорівнює декаді. Час регулювання залежить від частоти зрізу : чим більше , тим менше .

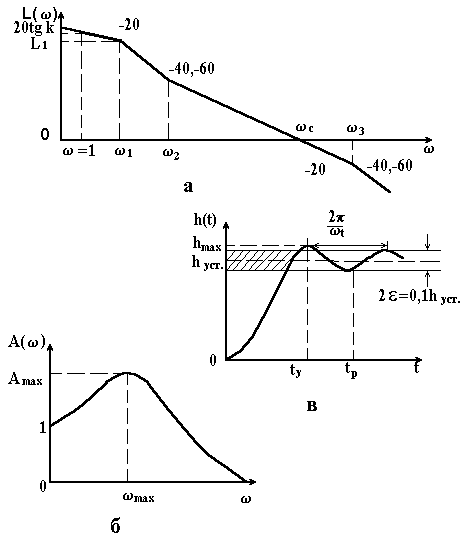
У зв’язку з можливістю оцінки якості процесу регулювання введені типові ЛАЧХ розімкнутих систем, які відрізняються одна від одної схилами окремих ділянок. Зазвичай розглядають чотири типи ЛАЧХ астатичних систем першого порядку (табл. 6.1). Кожна типова ЛАЧХ визначається чотирма параметрами (рис. 4.16, а), коефіцієнтом передачі розімкнутої системи k, частотами , , , при цьому . Та більш зручно кожну типову ЛАЧХ визначати ординатою , частотою зрізу і відносними частотами і . Кількісний зв’язок між показниками якості регулювання і параметрами типових ЛАЧХ наперед розрахований і зображується номограмами. Ці номограми дозволяють знайти , а отже, і і прямі показники якості перехідних процесів (рис. 4.16,
б і в), а також запас стійкості за фазою і коефіцієнти помилки і .

4.12 Інтегральні оцінки перехідних процесів

Прямі показники якості перехідного процесу характеризують окремі його сторони. Виникає питання: чи не можна перехідний процес оцінити тільки одним узагальненням критеріїв без посереднього визначення його окремих показників? Виявляється, можна. Таким узагальненням критеріїв є інтегральна оцінка перехідного процесу.

Інтегральна оцінка являє собою певний визначений інтеграл від деякої функції перехідної основної помилки. Переважно інтегральні оцінки застосовують для слідкуючих систем, які є астатичними. В цих системах встановлена помилка при ступінчастому задаючому впливі рівна нулю, і перехідна складова помилки рівна помилці системи

В загальному вигляді формула для визначення інтегральної оцінки має вигляд

. (4.25)

Рисунок 4.16 – Типова ЛАЧХ (а), АЧХ (б) і перехідна функція (в)

Для простої інтегральної оцінки знаходиться інтеграл

. (4.26)

Ця оцінка може бути застосована тільки для перехідних процесів перерегулювання, коли помилка не змінює свого знаку (рис. 4.17, а). Інтеграл визначає заштриховану частину на рис. 4.17, а, яку інколи називають площиною регулювання.

Рисунок 4.17 – Перехідна функція h(t) і помилка (t) при монотонному (а) і коливальному (б)

перехідних процесах

При коливальному характері перехідного процесу оцінка не може бути застосована, так як помилка має різні знаки. В цьому випадку застосовують інтегральну оцінку (рис. 4.17, б)

, (4.27)

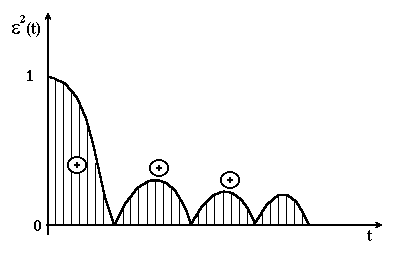
Вирахувати інтеграл дуже важко. Для оцінки як коливальних, так і монотонних перехідних процесів запропонована і часто застосовується квадратична інтегральна оцінка

, (4.28)

яка не залежить від знаку помилки, а отже, і від характеру кривої перехідного процесу. Інтеграл визначає заштриховану площу під кривою , яку інколи називають квадратичною площиною регулювання (рис. 4.18). Величина інтегралу буде тим менша, чим менша сума заштрихованих площин на рис. 4.18, тобто, чим більший перехідний процес до ідеальної ступінчастої видозміни регульованої величини, викликаний ступінчастою видозміною задаючого впливу.

Рисунок 4.18 – Графік зміни квадрата помилки

В результаті наближення перехідного процесу до ідеального (ступінчастого) отримується велика швидкість процесу при переході регульованої величини до нового встановленого значення, що викликає велике перерегулювання. Тому при оцінці перехідного процесу за інтегралом сильно коливальний процес може видатися кращим, ніж коливальний, а це не завжди є правильним.

Квадратичну інтегральну оцінку можна покращити, якщо враховувати не тільки помилку , але й швидкість її зміни . Такою оцінкою є інтеграл

. (4.29)

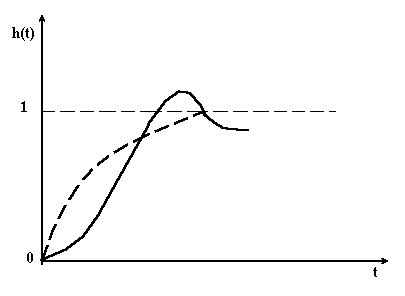
Можна довести, що мінімум інтегральної оцінки відповідає наближенню перехідного процесу не до ступінчатого, а до деякого експоненціального з постійною часу (пунктирна крива на рис. 4.19, яку називають екстремальною). Вибір параметрів системи із умови відповідає менш коливальному процесу в порівнянні з використанням квадратичної оцінки .

Рисунок 4.19 – Перехідний процес, відповідний мінімуму
інтегральної оцінки І

Знаходять застосування і більш інтегральні оцінки, враховуючи помилку , а також першу , другу і більш високі похідні від . При будь-яких інтегральних оцінках якість пересічного процесу буде тим краща, чим менша величина відповідного інтегралу.

Інтегральні оцінки вираховують через коефіцієнти відображення помилки.

4.13 Розрахунок сталої помилки автоматичної системи

Теорія автоматичного керування розглядає автоматичні системи в інформаційному плані, тобто з точки зору передачі і перетворення сигналів. Тому цілком природно виникає питання: з якою точністю передаються ці сигнали? Стосовно до цього, нас цікавить точність відтворення заданого впливу, тобто, з якою точністю виконується основна умова . Крім того, необхідно визначити помилку, викликану збудженням . Помилка системи від заданого впливу

а від збудження

тобто, помилка системи від збудження чисельно рівна зміні регульованої величини під впливом цього збудження (при відсутності заданого впливу).

За наявності перехідних процесів поточне значення помилки різко змінюється і не може служити мірою точності автоматичних систем. Тому домовились точність автоматичних систем оцінювати величиною сталої помилки, яка має місце в стійкій системі після закінчення перехідного процесу.

Отже, нам необхідно встановити, по-перше, як вираховуються сталі помилки і, по-друге, які фактори впливають на ці помилки. Обидва завдання будемо вирішувати паралельно. Попередньо зауважимо, що стала помилки вираховується для значення часу , тобто

Величину сталої помилки можна знайти із диференціального рівняння системи, але її значно зручніше вираховувати за допомогою передавальної функції помилки . Отже,

Дана формула дозволяє знайти зображення помилки. Для того, щоб знайти помилку як функцію часу, необхідно зробити зворотне перетворення Лапласа

звідки можна визначити сталу помилку прийнявши .

Та даний спосіб вираховування нераціональний, оскільки ми спочатку знаходимо помилку як функцію часу, а потім вираховуємо її значення для однієї тільки точки . А чи не можна відразу за відомим зображенням знайти , обійшовши проміжний етап визначення ? Виявляється, можна і до того ж досить просто. Для цього використаємо теорему операційного числення про кінцеве значення функції. Ця теорема свідчить про те, що, якщо відоме зображення функції , то кінцеве значення можна вирахувати за формулою

Використавши дану формулу для вирішення нашого завдання, отримуємо

. (4.30)

Формула (4.30) дозволяє вирахувати сталу помилку, що встановилася за заданим впливом . Для вилучення сталої помилки, що встановилася від збурення , треба користуватись залежністю

, (4.31)

де – передавальна функція за збуренням.

Таким чином, з формул (4.30) і (4.31) випливає, що наявність автоматичних систем залежить, по-перше, від зовнішнього впливу або і, по-друге, від властивостей автоматичної системи, що відтворюються передавальною функцією або .

В загальному випадку як заданий, так і збуджений впливи є складними функціями часу, при яких вирахування помилок значно ускладнюється і навіть є неможливим. Як же вийти з цього становища? Замінимо реальні впливи типовими, тобто достатньо простими для того, щоб можна було визначити помилки. По-перше, зовнішні впливи деяких систем близькі до типових, і по-друге, при проектуванні автоматичних систем необхідно порівнювати між собою різні варіанти і вибрати кращий.

Це зручно зробити при типових впливах, коли використовують ступінчасту , лінійну і квадратичну функції. Можна використовувати і більш складні впливи.

Всі ці впливи легко зобразити за допомогою формул, їх значення можна точно вирахувати для будь-якого моменту часу. Однак зовнішні впливи часто є випадковими функціями часу. В такому випадку для оцінки точності автоматичних систем використовують статичні методи.

4.14 Помилки від задаючих впливів

Отримаємо формулу для вираховування помилки від задаючих впливів. Враховуючи рівність (4.30), а також формулу для передавальної функції помилки

отримаємо

(4.32)

де – передавальна функція розімкнутої системи.

При вираховуванні помилки за формулою (4.32) необхідно мати на увазі, що зображення за Лапласом типових впливів для відповідно рівні

Крім того, для статичних систем . Для астатичних систем 1-го і 2-го порядків приймемо відповідно і . При цьому , де k – коефіцієнт передачі розімкнутої системи; – передавальна функція без врахування інтегруючих ланок і коефіцієнта передачі.

Розглянемо тепер помилки деяких автоматичних систем. Як видно із табл. 3, статичні системи при ступінчастому впливі мають сталу помилку

, (4.33)

яка називається статичною, або помилкою за станом. Вона пропорційна величині заданого впливу і зменшується із збільшенням коефіцієнта передачі розімкнутої системи k. При змінних у часі впливах помилка безперервно зростає, тому ці системи як слідуючі використовувати недоцільно.

Астатичні системи 1-го порядку принципово точно відпрацьовують ступінчастий вплив, але мають постійну помилку при відпрацюванні лінійно зростаючого сигналу (табл. 4.2). Це помилка

(4.34)

пропорційна швидкості v зміни вхідного сигналу, тому її називають швидкісною помилкою, а коефіцієнт передачі розімкненої системи k – добротністю системи за швидкістю. Відсутність статичної помилки пояснюється наявністю в одноланцюговій структурній схемі системи інтегруючої ланки.

Астатичні системи 2-го порядку принципово точно відпрацьовують як ступінчастий, так і лінійно зростаючий сигнал. При відпрацюванні квадратичного сигналу має місце помилка

(4.35)

пропорційна прискоренню а вхідного сигналу і обернено пропорційна коефіцієнту посилення розімкненої системи k, який називається добротністю системи за прискоренням.

Отже, із збільшенням коефіцієнта передачі розімкненої системи сталі помилки зменшуються. Але, як уже було сказано, із збільшенням k погіршується стійкість автоматичних систем. Таким чином, вимога до точності заперечує потребу до стійкості. Отже, при виборі величини k повинно бути прийняте компромісне рішення. Забігаючи наперед, зазначимо, що покращання стійкості при заданому відносно великому значенні k досягається шляхом включення до системи коректуючих пристроїв.

Відзначаючи вплив порядку астатизму системи v на точність, констатуємо, що чим більша v, тим точніше система відпрацьовує більш складний вплив. Однак ці системи більш схильні до коливань в перехідних процесах, їх стійкість погіршується. Тому системи з порядком астатизму більше двох на практиці майже не зустрічаються.

4.15 Коефіцієнти помилки

Якщо заданий вплив є функцією часу, що повільно змінюється, то динамічну помилку можна вирахувати за допомогою так званих коефіцієнтів помилки.

Передавальну функцію помилки можна запропонувати у вигляді ряду

(4.36)

Тоді

(4.37)

або в оригіналах

(4.38)

Таким чином, динамічна помилка системи складається із суми доданків пропорційних вхідному сигналу, його швидкості, прискоренню і т. д. , тому коефіцієнти називають коефіцієнтами помилки відповідно за станом, за швидкістю, за прискоренням і т. д.

Чим повільніше змішається вхідний сигнал, тим менше потрібно брати членів ряду в формулі (4.38).

Відомі декілька прийомів вирахування коефіцієнтів помилки. Найпростіше це зробити, розклавши передавальну функцію помилки в степеневий ряд шляхом ділення її чисельника на знаменник.

Слід відзначити, що порядок астатизму визначається кількістю перших коефіцієнтів помилки, рівних нулю. Так, для статичних систем () ні один з коефіцієнтів не дорівнює нулю, для статичних систем першого порядку , а для статичних систем другого порядку і .

4.16 Помилки від впливу збурення

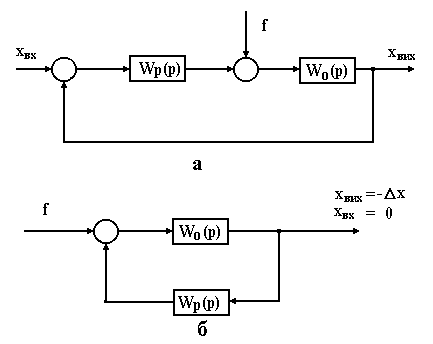
Для визначення помилок від збурення структурну систему необхідно привести до вигляду, показаного на рис. 4.20, де і – передавальні функції частин системи, умовно названі відповідно регулятором і об’єктом.

Рисунок 4.20 – Структурні схеми АСР

Передавальна функція за збуренням (рис. 4.20, б)

де – передавальна функція розімкнутої системи.

Тоді зображення у відповідності з формулою (4.31) має вигляд

. (4.39)

Використовуючи дану формулу, можна не тільки вирахувати величину сталої похибки, але й визначити порядок
астатизму системи по відношенню до збурення. Так, якщо регулятор не містить інтегруючої ланки, то система буде статичною, якщо містить – астатичною (рис. 4.21).

Рисунок 4.21 – Перехідні функції встановленої помилки за збуренням для астатичних (а) і

статичних (б) систем

Так, наприклад, при статичному об’єкті і статичному регуляторі і . При ступінчастому збуренні

З урахуванням того, що , стала похибка

(4.40)

де – коефіцієнт передачі розімкненої системи, тобто система статична.

Якщо ж регулятор буде астатичним, тобто , до того ж , то

, (4.41)

тобто система є астатичною.

Висновки: якість процесів регулювання – це загальна характеристика динамічних властивостей автоматичних систем як в перехідних процесах, так і в сталих режимах.

Перехідний процес обумовлюється інерційністю системи. Його можна оцінити прямо і непрямо.

При прямій оцінці тих чи інших способів необхідно будувати графік перехідного процесу, за яким знаходять основні його показники. Непрямі оцінки не потребують побудови графіків перехідного процесу і в цьому їх перевага. Вони дають можливість визначити деякі деталі перехідного процесу і встановити вплив системи на його якість.

Точність автоматичних систем характеризує вимушений рух, який оцінюється величиною встановлених помилок, які залежать як від характеру зовнішнього впливу, так і від якості самої системи. Зі збільшенням коефіцієнта передачі розімкнутої системи її помилки зменшуються, однак при цьому погіршується стійкість. Тому мають місце протиріччя в потребах до точності і стійкості.

Показники якості процесів регулювання мають забезпечити пред’явлені до системи вимоги. Це досягнення корекції динамічних систем.

СТІЙКІСТЬ АВТОМАТИЧНИХ СИСТЕМ І ПОКАЗНИКИ ЯКОСТІ ПЕРЕХІДНИХ ПРОЦЕСІВ