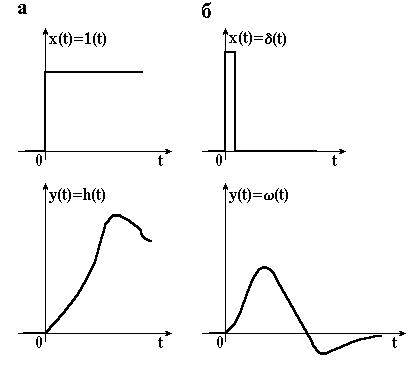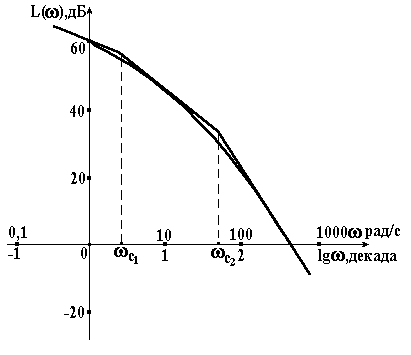СТАТИЧНІ І ДИНАМІЧНІ ХАРАКТЕРИСТИКИ ОБ’ЄКТІВ КЕРУВАННЯ

ЛЕКЦІЯ 2

2.1 Лінійні диференціальні рівняння автоматичних систем і їх елементів

Найбільш спільною і найбільш повною формою математичного описання автоматичних систем і їх елементів є диференціальне рівняння. Але для більшості реальних елементів вихідне рівняння, складене строго у відповідності з законами фізики, є нелінійним. Ця обставина сильно ускладнює всі наступні процедури аналізу. Тому завжди прагнуть перейти від складнішого розв’язання нелінійного рівняння до лінійного диференціального рівняння

(2.1)

де і – відповідно вхідна і вихідна величини елементу або системи; , 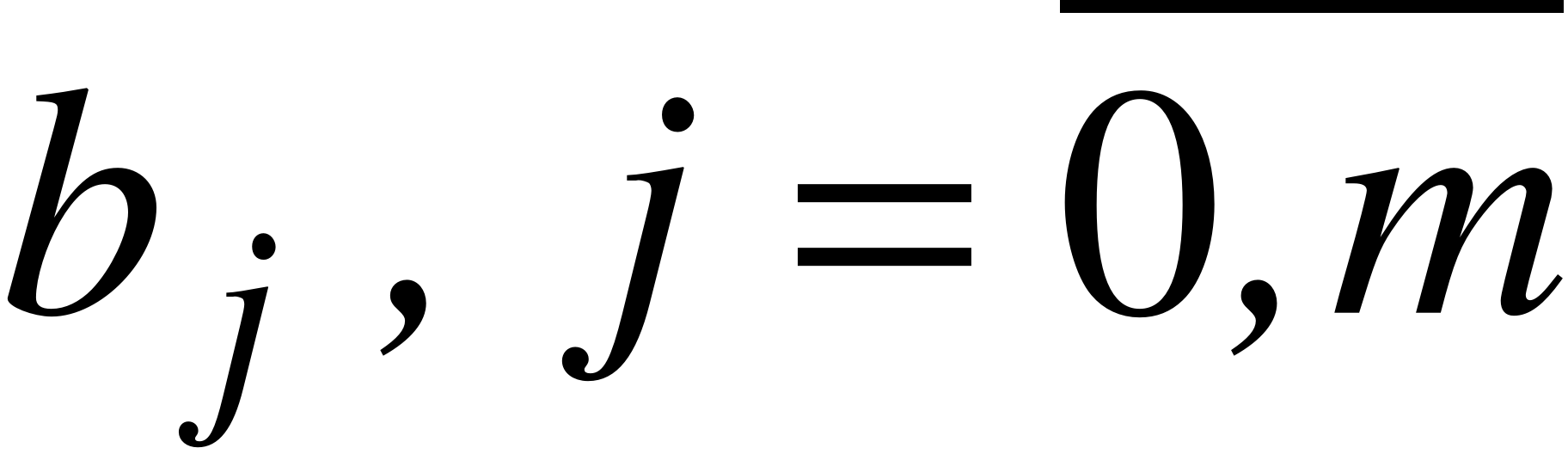– коефіцієнти рівняння.

Рівняння (2.1) встановлює зв’язок між вхідною величиною як в перехідних, так і в установлених режимах.

Коефіцієнти диференціального рівняння залежать від різних фізичних констант, що характеризують швидкість протікання процесів в елементах. Такими константами є, наприклад, маси частинок, що рухаються, індуктивності і ємності електронних ланцюгів, теплоємності нагрівальних елементів.

Інколи параметри деяких елементів систем змінюються в часі, причому швидкість їх зміни співставляється з швидкістю процесів управління в системі. Тоді систему називають нестаціонарною, або системою зі змінними параметрами. Системою зі змінними параметрами є, наприклад, автоматична система керування приводом повороту потужного екскаватора, якщо в процесі повороту одночасно виконується висування ручки з ковшом. В міру віддалення ковша від центра повороту платформи екскаватора сильно збільшується маховий момент маси навколо вертикальної осі і, отже, значно буде змінюватись один з коефіцієнтів диференціального рівняння.

В більшості практичних випадків коефіцієнти рівняння мало змінюються, і системи є системами з постійними параметрами. Далі будуть розглядатися тільки такі системи.

Якщо при складанні лінійного диференціального рівняння (2.1) використовуються лінеаризовані статичні характеристики або прийняті допущення про лінійності тих чи інших взаємозв’язків, то рівняння справедливе лише для малих відхилень вхідної і вихідної величин від їх значень в статичному режимі Але для спрощення записів часто в лінійному рівнянні відхилення позначають тими ж символами (без знаку ), що й самі величини.

Для автоматичних систем керування, що описуються лінійним рівнянням (2.1), справедливий принцип накладання або суперпозиції, згідно з яким зміна вихідної величини , що виникає при дії на систему декількох вхідних сигналів, дорівнює сумі зміни величини , що викликаються кожним сигналом окремо. Ця властивість лінійних систем має практичне значення, так як, дякуючи йому, значно полегшує всі розрахунки.

Розглянемо тепер типові форми запису лінійного диференціального рівняння (2.1), які використовуються в різних задачах теорії автоматичного управління.

Як і в інших галузях науки і техніки, всі фізичні змінні, які входять в рівняння, можуть бути виражені у відносних одиницях. Для цього кожний доданок ділять на сталу величину, що має розмірність тієї змінної , яка входить в цей доданок. Сталі величини називають базовими. Як базові величини приймають переважно номінальні або встановлені значення змінних х і у.

Вигідною формою запису лінійних диференціальних рівнянь є символічна або операторна. Перехід до цієї форми здійснюється введенням скороченого умовного позначення операції диференціювання: Відповідно коефіцієнту похідну змінної у позначають

, (2.2)

тоді рівняння (2.1) в символічній формі буде мати вигляд

. (2.3)

Многочлени від р степеня п і т, що знаходяться в лівій і правій частинах рівняння (2.3), називаються диференціальними операторами. Кожний такий оператор встановлює співвідношення між функцією часу і визначеною сукупністю похідних цієї функції. Многочлен

(2.4)

називають власним оператором, а многочлен

(2.5)

– вхідним оператором або оператором дії.

Назва “власний” обумовлена тим, що многочлен характеризує власний рух елемента, рух за відсутності внутрішньої дії. Оператор називають також характеристичним.

У всіх реальних елементах і системах порядок найвищої похідної в вхідному операторі не може бути більшим від порядку найвищої похідної в власному операторі, тобто, всі . Якщо в процесі яких-небудь формальних викладок утворюється рівняння, в якому , то вважають, що це рівняння відповідає фізично нереалізуючій системі.

Рівняння елементів невисокого порядку () в теорії автоматичного управління прийнято записувати в так званій стандартній формі. При стандартній формі запису рівняння перетворюється таким чином, щоб коефіцієнт при вихідній величині був рівний одиниці. При цьому коефіцієнт перед вхідною величиною в правій частині рівняння стає рівним передавальному коефіцієнту, а коефіцієнти при похідних вихідної величини будуть мати розмірність часу в степені, рівній порядку відповідної похідної. Наприклад, рівняння другого порядку

(2.6)

шляхом ділення всіх членів на коефіцієнт може бути приведене до стандартної форми

, (2.7)

де

Коефіцієнти називають сталими часу. Вони характеризують динамічні властивості елемента. Часто при дослідженні автоматичних систем виявляється вигідним перехід від природного часу t, виміряного в секундах, хвилинах, до так званого безрозмірного (відносного) часу . Цей перехід здійснюють за допомогою деякого сталого (в загальному випадку – довільно вибраного) множника , який має розмірність часу.

. (2.8)

Як множник часто беруть сталу часу одного з елементів, що входять в систему. Величину, обернену до множника , називають масштабом часу і позначають .

Оператор k-кратного диференціювання за безрозмірним часом зв’язаний із звичайним оператором диференціювання співвідношенням

(2.9)

Використовуючи співвідношення (2.9), можна будь-яке диференціальне рівняння записати в безрозмірному часі, який вимірюється в умовних одиницях . Наприклад, рівняння (2.6) буде мати вигляд

. (2.10)

Якщо коефіцієнт перетворення часу вибирають за визначеним правилом, а саме:

(2.11)

то можна максимально спростити диференціальне рівняння. Так, рівняння (2.10) набуде вигляду

, (2.12)

де

В лівій частині рівняння замість трьох числових коефіцієнтів залишився лише один коефіцієнт . Така компактна форма запису була вперше використана І.А.Вишнеградським (для рівняння 3-го порядку) і називається формою Вишнеградського.

Важливою перевагою цієї форми є те, що введення безрозмірного часу в диференціальне рівняння не впливає на характер функції (міняється тільки масштаб незалежної змінної t). Тому заміна масштабу часу широко використовується при дослідженні автоматичних систем на аналогових обчислювальних машинах. При цьому приходять як до “приско-рення” часу (), так і до “сповільнення” часу ().

Заміна масштабу часу полегшує в багатьох випадках аналіз динаміки автоматичних систем, дозволяє одержати результати в найбільш загальному, універсальному вигляді.

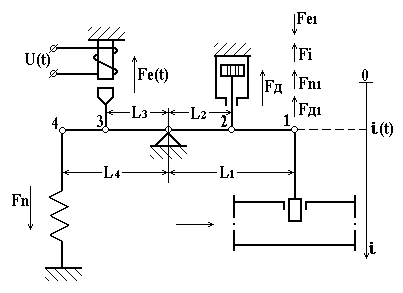
Приклад. Складемо і запишемо в типових формах диференціальне рівняння механічної частини виконуючого пристрою, зображеного на рис. 2.1. Сила , утворена електромагнітом і прикладена в точці 3, через важіль передається на виконавчий орган – заслінку. Вихідною величиною слід вважати переміщення заслінки , так як від величини переміщення залежать пропускна здатність трубопроводу і режим роботи всього наступного ланцюжка елементів автоматичної системи. (Зазначимо, що нерідко призначення електромагніта – створення тиску на об’єкт, і тоді як вихідну величину слід розглядати силу).

Згідно з відомим законом механіки – принципом Даламбера – сума всіх моментів, діючих на важіль, повинна дорівнювати нулю

(2.13)

Так як кут повороту важеля змінюється в невеликих межах, то замість обертового руху можна розглядати поступальний, а рівняння руху записати для лінійного переміщення однієї з точок важеля (наприклад, для точки 1). Відповідно всі сили і маси необхідно привести в дану точку. Тоді замість рівняння моментів (2.13) можна записати рівняння сил, приведених в точку 1

(2.14)

Рисунок 2.1 – Конструктивна схема електромагнітного виконавчого пристрою

Сила інерції пропорційна прискоренню в точці 1 і масі пересувних частинок пристрою

, (2.15)

де т – сума мас, приведених в точку 1, кг.

Силу демпфера з достатньою для практичних розрахунків точністю можна вважати пропорційною швидкості переміщення точки 2

, (2.16)

де – коефіцієнт демпфування, що залежить від конструктивних параметрів демпфера (площі поршня і діаметра дірок в ньому), Н/(м/с).

Сила пружності пружини пропорційна величині переміщення точки 4

, (2.17)

де – коефіцієнт пружності (жорсткості) пружини, Н/м.

Підставляючи вирази (2.15), (2.16), (2.17) у рівняння сил (2.14), одержимо диференціальне рівняння, котре зв’язує вхідну і вихідну величини механічної частини пристрою

(2.18)

Після ділення лівої і правої частини рівняння (2.18) на величину його можна записати в стандартній формі

, (2.19)

де – стала часу, яка характеризує коливальні властивості пристрою, с; – стала часу, яка характеризує демпфуючі властивості, с; – передавальний коефіцієнт пристрою, що залежить від пружності пружини і співвідношення плечей руки, м/Н.

При складанні рівняння (2.19) було прийнято, що сила тертя пропорційна швидкості переміщення і що ліве і праве плечі ручки не доходять до відказу. Обидва ці передбачення справедливі лише при обмеженому діапазоні зміни величин і їх похідних. Тому, хоч лінеаризація в явному вигляді і не здійснюється, рівняння (2.19) є в дійсності лінеаризованим і, отже, справджується лише для відхилень l і Fe вказаних величин від значень, котрі відповідають точкам лінеаризації або серединам діапазонів, які розглядаємо.

Запишемо тепер рівняння (2.19) у відносних одиницях. Для цього приймемо як базові значення змінних деякі сталі величини і і введемо позначення і . Тоді рівняння (2.19) після нескладних перетворень набуде вигляду

, (2.20)

де – безмежний передавальний коефіцієнт приладу.

Для того, щоб записати рівняння в безмежному часі, візьмемо за одиницю часу одну з сталих часу приладу, наприклад, величину . Тоді час, який вимірюється в одиницях ,

відповідно

диференціальне рівняння (2.20) матиме вигляд

(2.21)

де – безрозмірний коефіцієнт рівняння.

2.2 Перехідні функції

Диференціальне рівняння є найзагальнішою формою описування елемента і не дає уяви про передавальні властивості елемента. Уяву про ці властивості дає функція , яка є розв’язком диференціального рівняння. Але одне і те ж диференціальне рівняння може мати, як відомо, декілька розв’яз-ків, конкретний вигляд яких залежить від початкової умови і від характеру функції 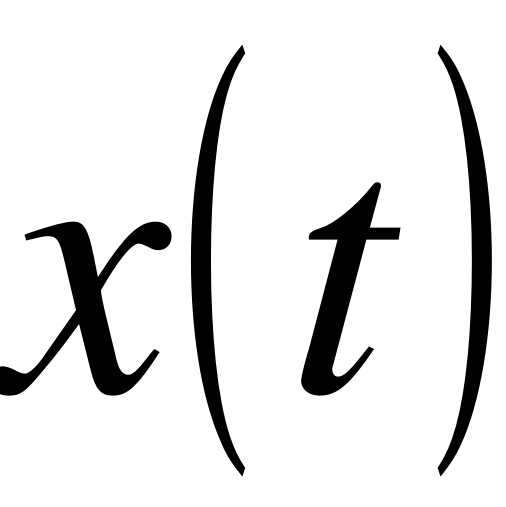, від початкового стану елемента і від виду внутрішньої дії. Тому прийнято динамічні властивості елементів і систем характеризувати розв’язком, відповідним нульовим початковим умовам (елемент знаходиться в статичному режимі) і одній з типових дій. Як типові дії приймають одиничну ступінчасту дельта-функцію або гармонічну функцію.

Найбільш уявлення про динамічні властивості елемента дає його перехідна функція (характеристика). Перехідною функцією називають зміну вихідної величини в часі, яка виникає після подання на вхід одиничної ступінчастої дії при нульових початкових умовах. Перехідна функція може бути задана у вигляді графіка (рис. 2.2, а) або у формульному вигляді. Формульний вираз функції для конкретного елемента можна знайти, розв’язуючи його диференціальне рівняння при і при Друга умова означає, що вихідна величина у і її похідні до ()-го порядку безпосередньо перед подачею ступінчастої дії дорівнюють нулю.

Рисунок 2.2 – Перехідна (а) та імпульсна перехідна (б) функції

Перехідна функція , як і будь-який розв’язок неоднорідного диференціального рівняння вигляду (2.1), має складові: вимушену і вільну . Вимушена складова перехідного процесу, є , як відомо, власним розв’язком вихідного рівняння. При ступінчастій дії вимушена складова рівна встановленому значенню вихідної величини, котре може бути визначене безпосередньо з диференціального рівняння (при )

(2.22)

Вільна складова може бути знайдена як розв’язок відповідного диференційного рівняння в наступному вигляді:

(2.23)

де – корені характеристичного рівняння; – постійні інтегрування, котрі залежать від початкових умов.

Характеристичне рівняння, яке відповідає диференціальному рівнянню, являє собою, як відомо, алгебраїчне рівняння, степінь і коефіцієнти якого співпадають з порядком і коефіцієнтами лівої частини цього диференціального рівняння. Для диференціального рівняння, записаного у формі (2.1), характеристичне рівняння має вигляд

. (2.24)

Структура характеристичного рівняння (2.24) співпадає з структурою лівої частини диференціального рівняння, записаного в символічній формі (2.3) і з структурою власного (характеристичного) оператора D(p) (2.4). Тому при записі характеристичного рівняння часто замість символу , котрий означає невідому заміну алгебраїчного рівняння, використовують символ р. Але при цьому р означає вже не операцію диференціювання, а деяке комплексне число, яке є розв’язком (коренем) характеристичного рівняння.

Для лінійних елементів і систем, крім принципу суперпозиції, справедливе ще одне загальне правило: реакція на неодиничну ступінчасту дію рівна похідній перехідної функції на величину множника а, . Ця властивість широко використовується при дослідженні і розрахунку лінійних систем.

Імпульсною перехідною функцією називають зміну вхідної величини , яка виникає після надання на вхід дельта-функції, при нульових початкових умовах (рис. 2.2, б).

Якщо вхідна дія являє собою неодиничний імпульс , ординати функції вихідної величини будуть в а разів більші ординат функції , .

Імпульсна перехідна функція рівна похідній від перехідної функції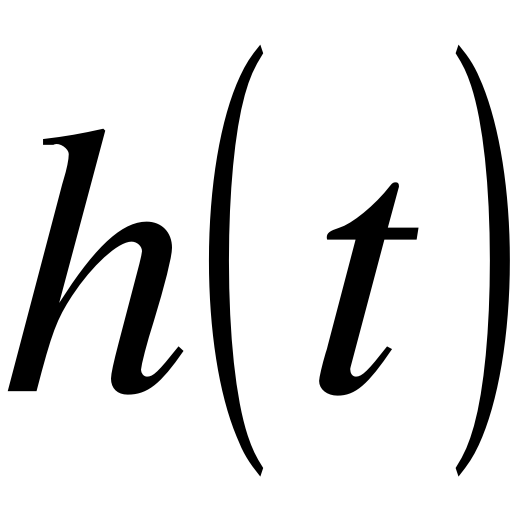

, (2.25)

і навпаки, перехідна функція рівна інтегралу від імпульсної перехідної

. (2.26)

За допомогою імпульсної системи перехідної функції елемента можна визначити його реакцію на вхідну дію вільного виду. Зв’язок між зміною вхідної і вихідної величин в часі встановлюється інтегралом Дюамеля, або інтегралом згортки

. (2.27)

Так як при вхідна дія , а при функція (умова фізичного виконання), то межі інтегрування у (2.27) можна вважати нескінченними

. (2.28)

Перехідні характеристики і називають також часовими.

Приклад 1. Знайдемо перехідну функцію елемента, який описується рівнянням

. (2.29)

Перехідна функція має дві складові

(2.30)

Вимушена складова згідно з (5.9) в даному випадку рівна

. (2.31)

Вільну складову будемо шукати у вигляді

(2.32)

Враховуючи початкову умову , одержимо Тоді

. (2.33)

Приклад 2. Визначимо за допомогою інтеграла Дюамеля реакцію елемента (2.29) на дію вигляду

Імпульсна перехідна функція елемента згідно з (2.25)

. (2.34)

Функцію , яка описує зміну вихідної величини після надання лінійної дії, одержимо, підставляючи вираз (2.34) в інтеграл (2.27)

(2.35)

2.3 Передавальні функції

Найбільш розповсюдженим методом описування і аналізу автоматичних систем є операційний. В основі методу лежить перетворення Лапласа

, (2.36)

яке встановлює відповідність між функціями дійсної змінної t і функціями комплексної змінної р. Функцію часу , яка входить в інтеграл Лапласа (2.36), називають оригіналом, а результат інтегрування – функцію – називають зображенням функції за Лапласом.

Перетворення Лапласа виконується лише для таких функцій часу, котрі рівні нулю при . Ця умова забезпечується, зазвичай, множенням функції на одиничну ступінчасту функцію . З математичної і фізичної точок зору такий штучний прийом повністю конкретний, так як функції описують процеси в автоматичних системах, які починаються з деякого моменту часу, а цей момент часу завжди може бути прийнятий за початок відліку.

В табл. 2.1 показані зображення простих функцій часу, які найчастіше використовуються в розрахунках автоматичних систем.

Таблиця 2.1 – Зображення простих функцій часу

Назва функції	x(t)	X(p)
Дельта-функція		1
Ступінчаста функція
Степенева функція
Експонента
Синусоїда
Косинусоїда

Основні властивості перетворення Лапласа показані в таблиці 2.2. Кожну з цих властивостей використовують при аналізі автоматичних систем операційним методом.

Найбільш важливими властивостями перетворення Лапласа є властивості, які формулюються, зазвичай, у вигляді правил: при нульових початкових умовах диференціювання оригіналу за змінною t відповідає множенню зображення на комплексну змінну р, а інтегрування оригіналу – діленню на р. Так, на цих двох властивостях оснований операційний метод розв’язку диференціальних рівнянь. Метод полягає в наступному. Вихідне диференціальне (або інтегродиференціальне) рівняння замінюють на алгебраїчне рівняння відносно зображення . Отже, замінюють на (цю процедуру називають алгебраїзацією диференціального рівняння), потім, розв’язуючи алгебраїчне рівняння при заданому , знаходять зображення і, накінець, за зображенням визначають функцію . Зворотний перехід від зображення до оригіналів в більшості практичних задач можна зробити за допомогою таблиць, які знаходяться в спеціальних довідниках з операційного обчислення.

Широке розповсюдження операційного методу в теорії автоматичного керування обумовленого ще й тим, що з його допомогою визначають так звану передавальну функцію, яка є найкомпактнішою формою описання динамічних властивостей елементів і систем.

Таблиця 2.2 – Основні властивості перетворення Лапласа

Назва	Оригінал	Зображення
Лінійність
Правило диференціювання (при нульових початкових умовах)
Правило інтегрування (при нульових початкових умовах)
Зміна масштабу часу (теорема подібності)
Зміщення аргументу оригіналу (теорема запізнення)
Зміщення аргументу зображення
Правило множення зображень (теорема згортки)
Теорема про початкове значення оригіналу
Теорема про значення оригіналу

Використаємо перетворення Лапласа до лінійного диференціального рівняння загального вигляду (2.1), припускаючи, що до подання зовнішньої дії система знаходилась в спокої, і що всі початкові умови рівні нулю. Використовуючи властивість лінійності і правило диференціювання (див. табл. 2.2) можна одержати алгебраїчне рівняння у вигляді:

, (2.37)

де

;

Порівнюючи рівняння (2.37) з рівнянням у символічній формі (2.3), можна помітити повну аналогію їх структур. Різниця рівнянь лише в значенні символа р: в першому рівнянні він означає операцію диференціювання, в другому – комплексну змінну.

Введемо тепер поняття передавальної функції. Передавальною функцією W(p) називають відношення зображення вихідної величини до зображення вхідної величини при нульових початкових умовах

. (2.38)

Для системи, яка описується рівнянням (2.1), передавальна функція рівна відношенню вхідного оператора до власного оператора

. (2.39)

З виразу (2.39) видно, що передавальна функція не залежить від виду вхідної дії і характеризує лише власні динамічні властивості елемента або системи.

Розглянемо тепер основні властивості і особливості, якими володіють передавальні функції автоматичних систем і їх елементів.

Передавальна функція встановлює зв’язок між вхідною і вихідною величиною як в динамічному, так і в статичному режимах.

Передавальна функція дійсних елементів являє собою правильний раціональний дріб, в якому степінь полінома, що знаходиться в чисельнику, менший або дорівнює степеню полінома знаменника . Всі коефіцієнти передавальної функції – дійсні числа, що характеризують параметри елемента.

Передавальна функція є функцією комплексної змінної , яка може при деяких значеннях змінної р перетворюватись в нуль або нескінченність. Значення змінної р, при якому функція перетворюється в нуль, називають нулем, а значення, при якому перетворюється в нескінченність – полюсом передавальної функції. Очевидно, що нулями передавальної функції є корені полінома , а полюсами – корені полінома 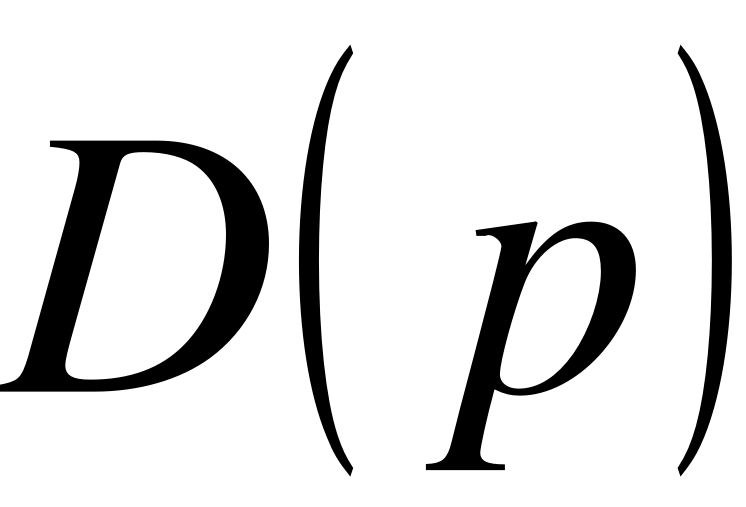. Корені поліномів чисельника і знаменника можуть бути комплексними, уявними і речовими числами (в тому числі і нульовими). Якщо ці корені відомі, то передавальна функція може бути представлена в такому вигляді

, (2.40)

де – корені многочлена (нулі ); – корені многочлена 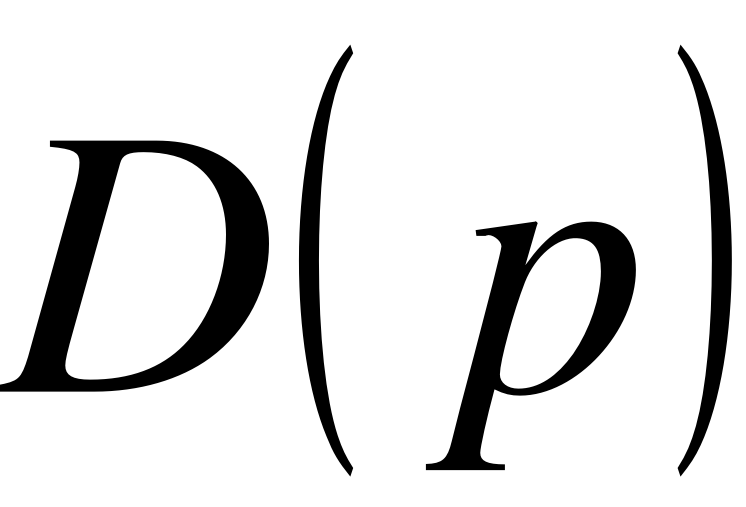(полюси ).

Таким чином, кожній конкретній передавальній функції з заданими коефіцієнтами відповідає визначеність сполучення нулів і полюсів. За розподіленням нулів і полюсів передавальної функції і комплексної площини з координатами і можна судити про властивості елемента або системи.

Якщо поліноми 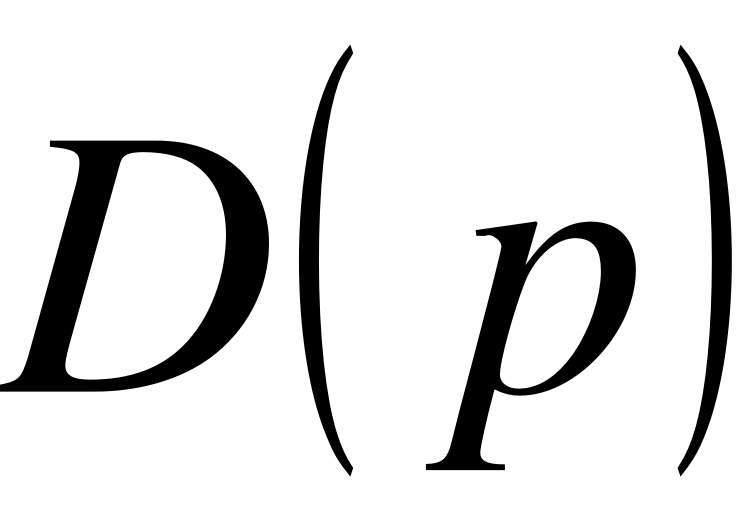і мають один або декілька нульових коренів, то передавальну функцію вигідно записувати в такій формі, щоб ці полюси і нулі були виділені в явному вигляді. Так, якщо передавальна функція має в точці полюс кратності v, то таку передавальну функцію можна записати у вигляді

, (2.41)

де при .

Передавальна функція (2.40) має полюси в точці , коли один або декілька менших коефіцієнтів многочлена рівні нулю: , (). Таку передавальну функцію можна представити у вигляді

, (2.42)

або після перетворень

, (2.43)

де при ; при ; .

Величину v називають порядком астатизму. Коефіцієнт k має розмірність

(2.44)

і з деякою умовою може бути названий передавальним коефіцієнтом. Умова полягає в тому, що поняття передавального коефіцієнта було введено як характеристика статичного режиму, а в елементах з статичного режиму роботи не існує.

Якщо , то елемент називається статичним, а його передавальна функція при рівна передавальному коефіцієнту

. (2.45)

Передавальна функція елемента пов’язана з його імпульсною перехідною функцією перетворення Лапласа

. (2.46)

У справедливості виразу (2.46) можна впевнитися, якщо врахувати, що функція характеризує зміну вихідної величини при і що зображення дельта-функції рівна 1.

2.4 Частотні характеристики

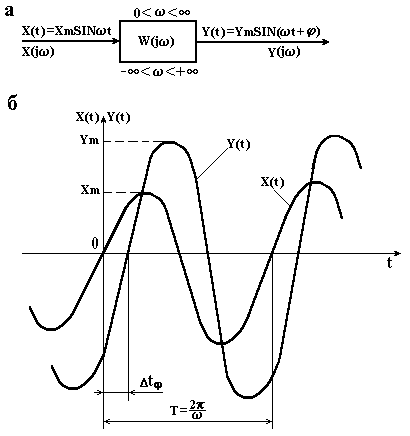
Частотні характеристики описують передавальні властивості елементів і систем в режимі встановлених гармонічних коливань, викликаних зовнішніми гармонічними діями. Знаючи частотну характеристику елемента, можна визначити його реакцію на гармонічну дію будь-якої частоти, а також на суму гармонічних дій різної частоти. Частотні характеристики широко використовуються в теорії і практиці автоматичного керування, так як реальні умови, що діють на автоматичні системи, можуть бути представлені як сума гармонічних сигналів. Позитивною властивістю частотних характеристик є те, що вони можуть бути безпосередньо визначені експериментальним шляхом. Розглянемо фізичну сутність і різновид частотних характеристик. Нехай на вхід лінійного елемента (рис. 2.3, а) в момент часу подано гармонічну дію відповідної частоти

. (2.47)

Через деякий час, необхідний для протікання перехідного процесу (для зникнення вільної складової), елемент ввійде в режим встановлених вимушених коливань, а вихідна величина буде змінюватись за гармонічним законом з тією ж частотою , але з іншою амплітудою і зі зрушенням по осі часу (рис. 2.3, б)

, (2.48)

де – фазове зрушення між вхідним і вихідним сигналами, град.

Повторюючи такий експеримент при фіксуючому для різних значень частоти (від 0 до ), можна встановити, що амплітуда і фазове зрушення вихідного сигналу конкретного елемента залежать від частоти дії. Подаючи гармонічну дію на вхід різних елементів, можна переконатися, що величини і залежать також від типу і параметрів елементу. Отже, залежності амплітуди і зрушення від значень частоти можуть служити характеристиками динамічних властивостей елементів.

Рисунок 2.3 – Визначення понять частотного методу

Так як амплітуда вихідного сигналу залежить ще від амплітуди вхідного сигналу , то доцільно при описанні передавальних властивостей елементів розглядати відношення амплітуд і .

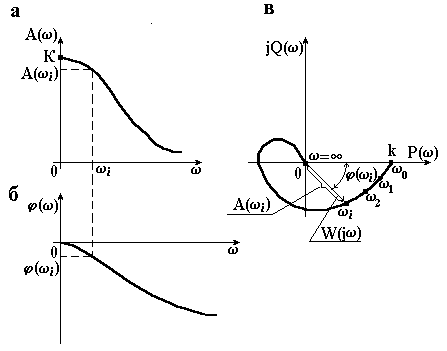
Залежність відношення амплітуд вихідного і вхідного сигналів від частоти називають амплітудною частотною характеристикою (скорочено АЧХ). Вона позначається . Залежність фазового зрушення між вхідним і вихідним сигналами від частоти називають фазовою частотною характеристикою (ФЧХ) . Можливий вид цих характеристик показаний на рис. 2.4, а і б. Аналітичні вирази і називають відповідно амплітудною і фазовою частотними функціями.

а – амплітудна; б – фазова; в – амплітудно-фазова

Рисунок 2.4 – Частотні характеристики

Амплітудна і частотна характеристики показують, як елемент пропускає сигнали різної частоти. Оцінку пропускання виробляють по відношенню амплітуд і . Фазова частотна характеристика показує, яке відставання і випередження вихідного сигналу по фазі створює елемент при різних частотах.

Амплітудна функція має розмірність, рівну відношенню розмірності вихідної величини до розмірності вхідної. В деяких випадках використовують безрозмірну функцію .

Амплітудну і фазову частотні характеристики можна об’єднати в одну загальну – амплітудно-фазову частотну характеристику (АФЧХ). Амплітудно-фазова частотна характеристика являє собою функцію комплексного змінного , модуль якої рівний , а аргумент рівний . Кожному фіксованому значенню частоти відповідає комплексне число , яке на комплексній площині можна зобразити вектором, що має довжину і кут повороту (рис. 2.4, в). Негативні значення , що відповідають відставанню вихідного сигналу від вхідного, прийнято відраховувати за годинниковою стрілкою від позитивного напряму дійсної осі.

При зміні частоти від нуля до нескінченності вектор буде повертатися навколо початку координат, одночасно буде збільшуватися або зменшуватися довжина вектора. Крива, яку при цьому опише кінець вектора, і є амплітудно-фазовою характеристикою. Кожній точці характеристики відповідає відповідне значення частоти. Проекції вектора на дійсну і уявну осі називають відповідно дійсною частотною характеристикою і уявною частотною характеристикою. Позначають їх так: . Зазначимо, що дійсна частотна характеристика завжди парна функція частоти, а уявна характеристика – завжди непарна функція.

Амплітудно-фазова функція , як і будь-яка комплексна величина, може бути представлена в показниковій

(2.49)

або в алгебраїчній формі

. (2.50)

Зв’язок між різними частотними функціями наступний:

, (2.51)

. (2.52)

Аналітичний вираз для амплітудно-фазової характеристики конкретного елемента можна одержати з його передавальної функції підстановкою

. (2.53)

Оскільки амплітудно-фазова функція , як і передавальна функція, являє собою звичайний дріб, то її модуль може бути знайдений за відомим правилом: як відношення модуля чисельника до модуля знаменника:

, (2.54)

а аргумент функції – як різниця аргументів чисельника і знаменника

. (2.55)

Амплітудно-фазова характеристика встановлює зв’язок між вхідним і вихідним сигналами не тільки для випадку, коли вони є гармонічними функціями, але і тоді, коли мають довільний вигляд. Вона рівна відношенню зображення за Фур’є вихідної величини до зображення вхідної величини

. (2.56)

В цьому випадку змінна змінюється від - до +, так як будь-який реальний сигнал може бути розкладений на суму тільки попарно спряжених векторів, що обертаються.

Користуючись співвідношенням (2.56) та зворотним перетворенням Фур’є, можна встановити зв’язок між частотними і часовими характеристиками. Врахуємо, що при вихідна величина і зображення за Фур’є дельта-функції рівне 1. Тоді імпульсну функцію можна записати так:

. (2.57)

Відповідно амплітудно-фазова функція є зображенням за Фур’є імпульсної перехідної функції

. (2.58)

Так як при функція , то нижня межа інтегрування прийнята рівною нулю.

Якщо (2.58) використати для імпульсної перехідної функції, записаної в безвимірному часі , то амплітудно-фазова характеристика стане функцією безвимірної частоти

, (2.59)

де – масштабний множник, прийнятий за одиницю часу.

Співвідношення (2.59) означає, що якщо розтягувати (стискати) графік функції вздовж осі часу в разів, то графіки амплітудної і фазової характеристик будуть стискатися (розтягуватися) вздовж осі частот в разів. Ця властивість використовується при побудові безвимірних частотних характеристик і при аналізі зв’язку перехідних процесів з частотними характеристиками систем.

При практичних розрахунках автоматичних систем вигідно використовувати частотні характеристики побудови в логарифмічній системі координат. Такі характеристики називають логарифмічними. Вони мають меншу кривизну і тому можуть бути приблизно замінені ламаними лініями, складеними з декількох прямолінійних відрізків. Причому ці відрізки в більшості випадків вдається побудувати без громіздких обчислень, за допомогою декількох простих правил. Крім того, в логарифмічній системі координат легко знаходити характеристики різних з’єднань елементів, так як множенню і діленню звичайних характеристик відповідають додавання і віднімання ординат логарифмічних характеристик.

За одиницю довжини по осі частот логарифмічних характеристик приймають декаду. Декада – інтервал частот, розташований між самовільним значенням і його десятикратним значенням . Відрізок логарифмічної осі частот, що відповідає одній декаді, рівний 1. Переважно, в розрахунках використовують логарифмічну амплітудно-частотну характеристику (ЛАЧХ)

, (2.60)

ординати якої вимірюють в логарифмічних одиницях – белах або децибелах (скорочено дБ).

Бел – одиниця вимірювання відношення потужностей двох сигналів. Якщо потужність одного сигналу більша (менша) потужності другого сигналу в 10 разів, то ці потужності відрізняються на (). Так як потужність гармонічного сигналу пропорційна квадрату його амплітуди, то при використанні цієї одиниці для вимірювання відношення амплітуд перед логарифмом з’являється множник 2. Наприклад, якщо на деякій частоті , то це означає, що потужності вхідного і вихідного сигналів відрізняються в 1002 разів, на або на відповідно і .

При побудові фазової частотної характеристики логарифмічний масштаб використовують тільки для осі абсцис.

На рис. 2.5 показані логарифмічна амплітудна характеристика (товста лінія) і відповідна їй наближена характеристика у вигляді прямолінійних відрізків (тонка лінія). Частоти, що відповідають точкам стику відрізків, називають сполучними і позначають .

Правила і приклади побудови наближених логарифмічних характеристик конкретних елементів будуть дані в главі 4.

За видом частотних характеристик всі елементи і системи діляться на дві групи: мінімально-фазові і немінімально-фазові. Мінімально-фазовими є елементи (системи), в яких всі полюси і нулі передавальної функції мають негативні і рівні нулю дійсні частини. Такі елементи дають мінімальний фазовий зсув порівняно з будь-якими іншими елементами, які мають таку саму амплітудну характеристику , але дійсна частина хоча б одного полюса або нуля якої додатна.

Мінімально-фазові елементи володіють цінною для практичних розрахунків властивістю: їх частотна передавальна функція повністю визначається однією з трьох складових: , або . Це істотно полегшує завдання аналізу і синтезу мінімально-фазових систем.

Рисунок 2.5 – Логарифмічна амплітудна частотна характеристика

Приклад. Знайдемо аналітичний вираз для частотних характеристик елемента, передавальна функція якого має вигляд

. (2.61)

Амплітудно-фазова функція елемента

. (2.62)

Вираз для амплітудно-частотної характеристики знайдемо як відношення модулів

, (2.63)

а для фазової – як різницю аргументів чисельника і знаменника

(2.64)

2.5 Статичні характеристики типових з’єднань елементів

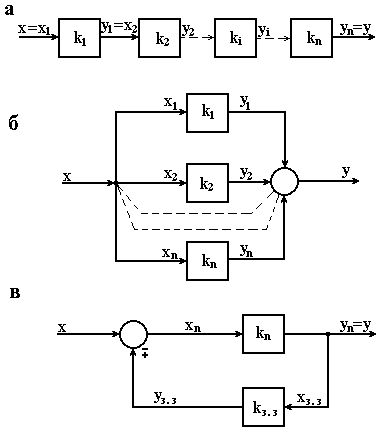
Алгоритмічна структура будь-якої автоматичної системи управління являє собою комбінацію трьох типових з’єднань елементів: послідовної, паралельної і обернено-паралельної дії. Кожне з’єднання може бути за простими правилами замінене одним елементом, статичні і динамічні властивості якого еквівалентні властивостям з’єднання.

При послідовному з’єднанні (рис. 2.6, а) вихідна величина кожного попереднього елемента є вхідною для наступного (і тільки для нього одного). Якщо елементи лінійні і в статиці характеризуються передавальними коефіцієнтами , то згідно з визначенням передавального коефіцієнта можна записати систему рівнянь

(2.65)

Викидаючи з (2.65) проміжні змінні , одержимо рівняння

, (2.66)

з якого випливає, що передавальний коефіцієнт еквівалентного елемента

а – послідовне; б – паралельне;
в – зустрічно-паралельне (із зворотним в’язком)

Рисунок 2.6 – Типові з’єднання елементів

. (2.67)

Таким чином, загальний передавальний коефіцієнт послідовно з’єднаних елементів рівний добутку передавальних коефіцієнтів цих елементів. Розмірність загального передавального коефіцієнта рівна добутку розмірностей коефіцієнтів.

Так як при послідовному з’єднанні вихід кожного попереднього елемента є входом наступного, то передавальні коефіцієнти всіх елементів повинні визначатися лінеаризацією статичних характеристик в точках, які відповідають одному і тому ж режиму.

Паралельним з’єднанням називають таке з’єднання, при якому на вхід всіх елементів поступає одна і та ж дія, а їх вихідні величини (з відповідними знаками) підсумовуються (рис. 2.6, б). Згідно з цим визначенням

(2.68)

(2.69)

Підставляючи в (2.69) рівняння статики окремих елементів

(2.70)

одержимо

(2.71)

Звідси випливає, що еквівалентний передавальний коефіцієнт паралельно з’єднаних елементів рівний сумі передавальних коефіцієнтів елементів

. (2.72)

Відзначимо, що підсумування сигналів в одній точці можливе лише в тому випадку, коли вони мають однакову розмірність. Тому коефіцієнти всіх паралельно включених елементів і коефіцієнтів завжди мають одну і ту ж розмірність.

Обернено-паралельним з’єднанням двох елементів (з’єднанням з оберненим зв’язком) називають таке з’єднання, при якому вихідний сигнал першого елемента поступає на вхід другого, а вихідний сигнал другого елемента з вхідним знаком підсумовується з загальним вхідним сигналом (рис. 2.6, в). Перший елемент, в якому напрям подачі сигналу співпадає з напрямом передачі загального сигналу, називають елементом прямого ланцюга. Другий елемент, в якому напрям передачі сигналу протилежний напряму передачі загального сигналу, називають елементом зворотного зв’язку.

Залежно від знаку сигналу зворотного зв’язку розрізняють позитивні і негативні зворотні зв’язки. Якщо сигнал зворотного зв’язку підсумовується (на схемі знак “+”) з загальним вхідним сигналом х, то зворотний зв’язок є позитивним. Якщо сигнал зворотного зв’язку віднімається від загального сигналу (на схемі знак “–“), то зворотний зв’язок є негативним.

Розглянемо статичні властивості з’єднання зі зворотним зв’язком. Нехай елементи прямого і зворотного зв’язків лінійні і характеризуються коефіцієнтами і . Тоді згідно з визначенням поняття “зворотний зв’язок” можна записати рівняння прямого ланцюга

, (2.73)

зворотного зв’язку

(2.74)

і вузла підсумування

(2.75)

Підставляючи вираз (2.74) в (2.75), а потім вираз (2.75) в (2.73), одержимо рівняння статики всього з’єднання із зворотним зв’язком

. (2.76)

Звідси еквівалентний передавальний коефіцієнт

, (2.77)

де знак “+” відповідає негативному зворотному зв’язку, а знак “–“ – позитивному.

З виразу (2.77) випливає, що негативний зворотний зв’язок зменшує еквівалентний коефіцієнт, а позитивний - збільшує. Якщо при позитивному зворотному зв’язку добуток коефіцієнтів рівний одиниці, то коефіцієнт зростає до нескінченності.

З’єднання з негативним зворотним зв’язком володіє позитивною (доброю) властивістю: при достатньо великому добутку величина еквівалентного передавального коефіцієнта практично не залежить від коефіцієнта .

Справді, при

. (2.78)

Ця властивість широко використовується при конструюванні високо стабільних приладів з елементів зі змінними коефіцієнтами.

Оцінимо вплив нестабільності коефіцієнта на спричинені ним зміни вихідної величини в двох випадках: коли елемент прямого ланцюга діє без зворотного зв’язку і коли він охоплений негативним зворотним зв’язком.

Нехай без зворотного зв’язку деякому фіксованому значенню відповідає значення , а в з’єднанні із зворотнім зв’язком таке ж значення вихідна величина приймає при значенні вхідної величини, рівному . Приріст вихідної величини, який виникає через зміни коефіцієнта на величину ,

. (2.79)

В з’єднанні зі зворотним зв’язком така ж зміна коефіцієнта створить приріст вихідної величини

. (2.80)

Враховуючи умову вибору значення , можна приріст виразити через приріст

. (2.81)

Вираз (2.81) показує, що негативний зворотний зв’язок зменшує відхилення вихідної величини, яке виникає через нестабільність коефіцієнта прямого ланцюга, в разів.

Приведені викладки ілюструють стабілізуючі дії негативного зворотного зв’язку при параметричному збуренні – при зміні параметра охоплюючої ланки. В главі 6 буде показано, що негативний зворотний зв’язок стабілізує вихідну величину і при координатних збуреннях. Саме дякуючи цьому, негативний зворотний зв’язок лежить в основі всіх замкнутих систем керування.

Розглянемо тепер методи одержання еквівалентних статичних характеристик з’єднань, які складаються з нелінійних елементів. В цьому випадку не можна використовувати формули (2.67), (2.72) і (2.77), еквівалентні характеристики доводиться визначати графічно.

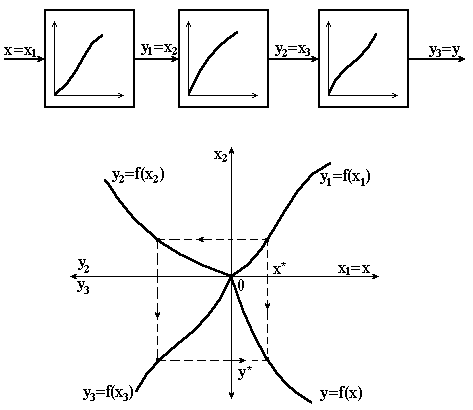
На рис. 2.7 показано, як можна послідовним переносом точок побудувати еквівалентну статичну характеристику послідовного з’єднання трьох елементів з нелінійними характеристиками (рис. 2.7, а).

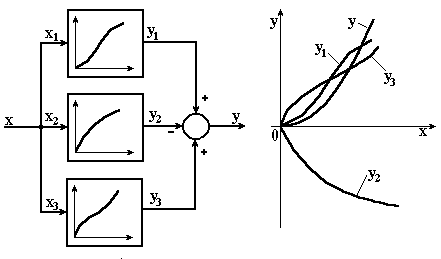
На рис. 2.8, б показано побудову еквівалентної характеристики паралельного з’єднання трьох нелінійних елементів (рис. 2.8, а). Вихідні сигнали першого і третього елементів підсумовуються, а вихідний сигнал другого – віднімається.

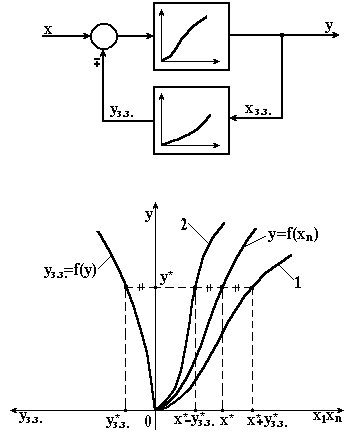
Тепер розглянемо зустрічно-паралельне з’єднання (рис. 2.9, а). В першому квадранті на рис. 2.9, б побудована характеристика елемента прямого ланцюга , а в другому квадранті – характеристика елемента зворотного зв’язку . Прослідкуємо, як будується еквівалентна характеристика при негативному зворотному зв’язку. Задамося деяким фіксованим значенням y* вихідної величини і визначимо, чому повинен дорівнювати вихідний сигнал х з’єднання. За характеристикою зворотного зв’язку знаходимо значення y*зз, яке відповідає значенню y*. Значення y*зз сигналу зворотного зв’язку віднімається від вхідного сигналу, тому значення вхідного сигналу повинно бути рівне .

Повторюючи цю процедуру для кількох значень вихідної величини, отримаємо характеристику з’єднання з негативним зворотним зв’язком (лінія 1).

За допомогою аналогічних міркувань і побудови можна отримати еквівалентну характеристику для додаткового зворотного зв’язку (лінія 2).

Рисунок 2.7 – Побудова статичної характеристики послідовного з’єднання елементів

Рисунок 2.8 – Побудова статичної характеристики
паралельно з’єднаних елементів

Рисунок 2.9 – Побудова статичної характеристики елемента,
охопленого зворотним зв’язком

СТАТИЧНІ І ДИНАМІЧНІ ХАРАКТЕРИСТИКИ ОБ’ЄКТІВ КЕРУВАННЯ