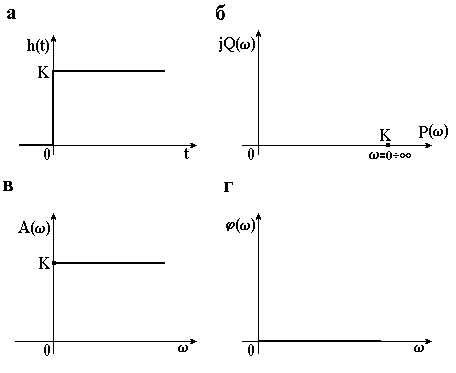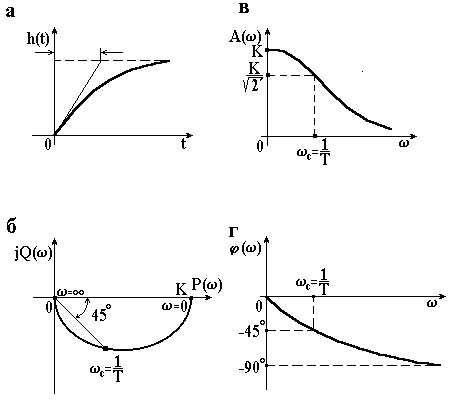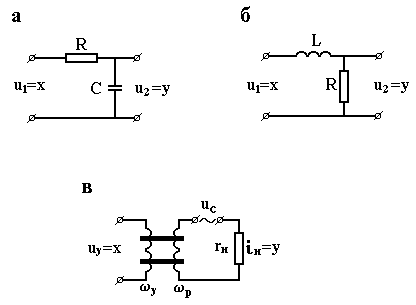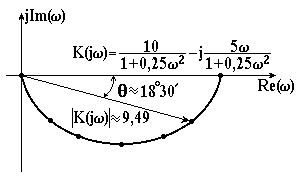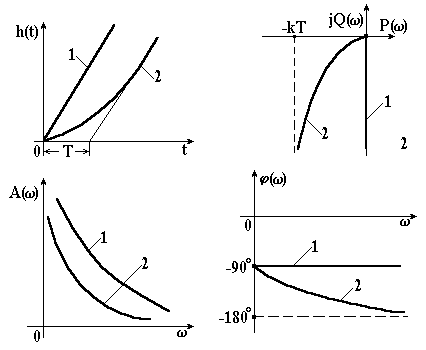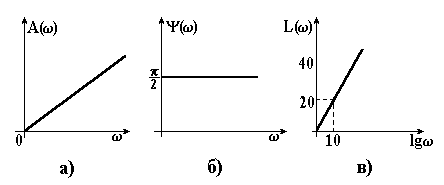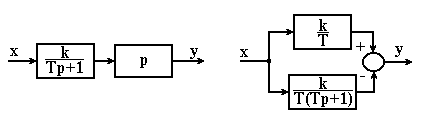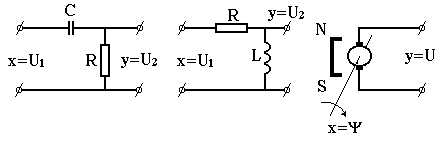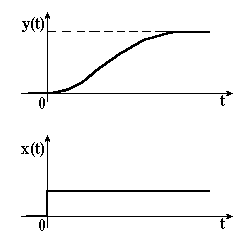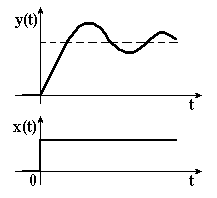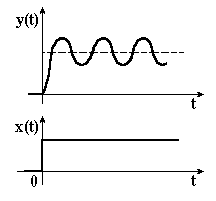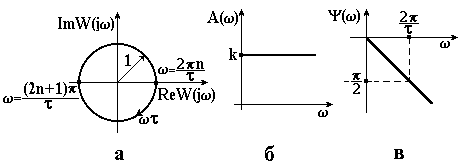Типові алгоритмічні ланки, їх частотні та часові характеристики

ЛЕКЦІЯ 3

3.1 Поняття алгоритмічної, типової і елементарної ланок

Багато технічних наук використовують умовні поняття для вирішення науково-технічних задач. Наприклад, в електротехніці користуються R, L, C і з їх допомогою проводять розрахунок електричних ланцюгів.

Аналогічно і в ТАК: систему керування можна синтезувати на основі типових динамічних ланок. Для цього використовують знання вищої математики, а саме: перетворення Лапласа, Фур’є та інші.

При вивченні роботи автоматичних систем ми класифікували елементи за функціональними ознаками. Це давало можливість вивчити взаємодію керованого об’єкта з керуючим пристроєм, а також їх елементів. Можна класифікувати елементи за динамічними властивостями. Така класифікація спрощує розв’язок задач аналізу. Виявляється, що незважаючи на розмірність елементів, багато з них мають однакові динамічні властивості.

Наприклад, двигуни постійного і змінного струмів після їх включення набирають швидкість за таким законом, за яким проходить зміна струму в їх обмотках. Всі ці процеси описуються диференціальними рівняннями першого порядку. В цьому проявляється єдність природи.

Загальність математичних виразів, що зв’язують вхідні і вихідні величини різних елементів, дозволяють виділити обмежену кількість типових алгоритмічних ланок.

Кожному типу алгоритмічної ланки відповідає математичне співвідношення між вхідною і вихідною величинами. Якщо ці співвідношення є елементарними, то такі алгоритмічні ланки називають елементарними.

Алгоритмічні ланки, які описуються звичайними диференціальними рівняннями І-го і ІІ-го порядку, називаються типовими динамічними ланками.

Типові динамічні ланки – це ланки спрямованої дії. Сигнали передаються тільки з входу на вихід. При зміні вхідного сигналу повинен змінюватись вихідний сигнал. Причому, якщо ланки з’єднані між собою, то наступна ланка не повинна впливати на попередню. Але ця вимога виконується не завжди.

При створенні класифікації динамічних ланок виникає проблема – скільки повинно бути ланок? Ця задача вирішена в 1938 році Михайловим. Він довів, що класифікація типових динамічних ланок може бути виконана на основі диференціального рівняння ІІ-го порядку:

. (3.1)

З цього рівняння можна отримати 12 рівнянь шляхом зміни коефіцієнтів (табл. 3.3).

Аналіз великої кількості елементів системи автоматичного керування вказує, що більшість з них мають динамічні властивості, які можна описати диференціальними рівняннями другого порядку.

Ланки, в яких , мають властивості статизму, тобто однозначний зв’язок між входом і виходом в статичному режимі. Тому її називають статичними або позиційними. До них відносяться 1, 2, 3, 4, 10, 11, 12. Ланки, в яких , мають властивості інерційності (2, 3, 4, 6, 8, 11, 12). Ланки 1, 5, 7 мають два коефіцієнти, які не дорівнюють нулю – ці ланки називають елементарними. Всі інші ланки можуть бути створені з елементів шляхом послідовного, паралельного, зустрічно-паралельного з’єднань.

В диференціальному рівнянні ІІ-го порядку, яке розглядається, всі коефіцієнти додатні. Виникає проблема – як зміняться властивості елементів, якщо хоч би один із коефіцієнтів диференціального рівняння від’ємний. Відповідь можна отримати, розглянувши хоча б одне диференціальне рівняння І-го порядку

Перетворимо його за Лапласом

, ,

Щоб знайти перехідні характеристики, потрібно взяти зворотне перетворення за Лапласом

Тоді .

Побудувавши графік (рис. 3.1), бачимо, що така ланка нестійка.

Рисунок 3.1 – Перехідна характеристика нестійкої ланки 1-го порядку

3.2 Типові ланки з розподіленими параметрами

Для систем, які мають елементи з розподіленими параметрами, краще виділити ряд типових елементів.

В літературі відсутня єдина класифікація, тому за основу візьмемо класифікацію Лозинського Л.Д., Ливаново Ю.В., яка приведена в книжці: “Аналіз і шляхи вдосконалення систем автоматичного регулювання об’єктів нафтогазової промисловості”. – М., 1978.

Ірраціональні ланки:

– напівінтегруюча;

– напіваперіодична І-го типу;

– напіваперіодична ІІ-го типу.

Експоненціальні ланки:

якщо то ланка чистого запізнення,

якщо то ланка затухання.

Гіперболічні ланки:

, де ;

;

3.3 Безінерційна ланка

Безінерційна ланка є найпростішою серед всіх типових ланок. Вона передає сигнал з входу на вихід моментально, без викривлення його форми. В ланці може відбуватися тільки посилення або послаблення моментальних значень вхідної величини.

Зв’язок між моментальним значенням вхідної величини і вихідної величини описується алгебраїчним рівнянням

. (3.2)

Передавальні властивості ланки визначаються лише одним параметром – передавальним коефіцієнтом k.

При одиничній ступінчастій дії , прикладеній в момент , вихідна величина моментально зміниться і прийме значення k (рис. 3.2). Перехідна функція ланки має вигляд

, (3.3)

а імпульсна перехідна

. (3.4)

Рівняння ланки в операційній формі

, (3.5)

звідси передавальна функція

. (3.6)

Рисунок 3.2 – Характеристика безінерційної ланки

Амплітудно-фазова характеристика ланки описується функцією

, (3.7)

якій на комплексній площині відповідає одна точка на дійсній осі (рис. 3.2). Амплітудна частотна характеристика така

, (3.8)

являє собою пряму, паралельну до осі частот (рис. 3.2, в). Це означає, що сигнали будь-якої частоти (від нуля до нескінченності) проходять через безінерційну ланку з однаковим відношенням амплітуд вхідної і вихідної величин, рівних k.

Вираз для фазової частотної характеристики (рис. 3.2,г)

(3.9)

показує, що безінерційна ланка не створює фазових зсувів між вхідною і вихідною величинами. Це і оправдовує назву ланки.

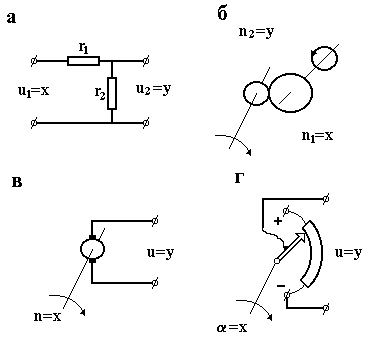
На рис. 3.3 зображені розповсюджені конструктивні елементи автоматичних систем, які є безінерційними ланками.

Рисунок 3.3 – Приклади безінерційних ланок

Передавальний коефіцієнт ненавантаженого дільника напруження (рис. 3.3, а)

. (3.10)

Передавальний коефіцієнт редуктора (рис. 3.3, б) залежить від співвідношення діаметрів або кількості зубців веденої і ведучої шестерень

. (3.11)

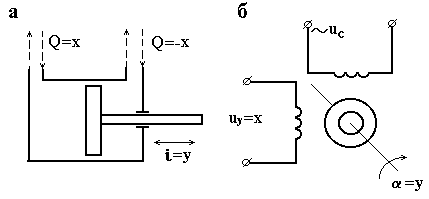
На рис. 3.3, в зображений тахогенератор, який використовується як вимірювач частоти повертання. Його вхідною величиною є частота обертання п, яка вимірюється в оборотах в секунду (1/с), а вихідною – напруга u, В. Передавальний коефіцієнт тахогенератора залежить від числа пар полюсів р, числа провідників в пазах якоря N, числа пар паралельних віток обмотки якоря а і магнітного потоку збудження Ф (у веберах)

(3.12)

У серійних тахогенераторах коефіцієнт знаходиться в межах від 1 до 10 .

Потенціометр (рис. 3.3, г) використовують для пропорційного перетворення кутового переміщення в електричну напругу u. Передавальний коефіцієнт потенціометра залежить від величини напруги , підведеного від внутрішнього джерела до затискачів потенціометра і від величини повного ходу двигуна

, В/градус . (3.13)

Безінерційними ланками є, як правило, приймаючі елементи (датчики), які використовуються в системах управління інерційними технологічними об’єктами.

Слід зазначити, що поняття безінерційної ланки є продуктом математичної ідеалізації. Насправді, всі реальні конструктивні елементи автоматичних систем володіють деякою інерційністю, так як передача енергії з входу на вихід елемента не може здійснюватись моментально.

Але, якщо інерційність того чи іншого елемента на 2-3 порядки менша, ніж в інших елементах розглянутої системи, то його вважають безінерційною ланкою.

3.4 Інерційна ланка І-го порядку

Диференціальне рівняння ланки має вигляд

, (3.14)

де k – передавальний коефіцієнт, який характеризує властивості ланки в статичному режимі; Т – стала часу, яка характеризує інерційність ланки.

Перехідну функцію ланки можна знайти, як суму загального і часткового розв’язків рівняння. Використовуючи відому методику, одержимо наступний вираз для перехідної функції:

. (3.15)

Графік перехідної функції зображений на рис. 3.4, а. За допомогою методів аналітичної геометрії неважко переконатися в тому, що дотична до кривої в точці відсікає на горизонтальній прямій відрізок, рівний сталій часу Т. Перехідна функція при рівна , а при функція досягає значення . В приблизних розрахунках зазвичай вважають, що при перехідний процес практично закінчився.

Рисунок 3.4 – Характеристика інерційної ланки І-го порядку

Імпульсна перехідна функція ланки може бути одержана шляхом диференціювання функції . Для інерційної ланки першого порядку імпульсна функція має вигляд

. (3.16)

Застосовуючи до лівої і правої частин рівняння перетворення Лапласа, одержимо рівняння динаміки ланки в операційній формі

. (3.17)

З рівняння (3.17) знаходимо передавальну функцію ланки

. (3.18)

Підставляючи в передавальну функцію , одержимо амплітудно-фазову функцію

. (3.19)

Перемножуючи чисельник і знаменник функції на вираз , спряжений із знаменником, можна позбутися величини j в знаменнику і представити амплітудно-фозову функцію у вигляді суми дійсної і уявної частин

, (3.20)

де

(3.21)

Вираз (3.21) можна розглядати як рівняння амплітудно-фазові характеристики , задане в параметричній формі в системі координат і . Роль третьої змінної (параметра) відіграє частота .

Якщо виразити уявну складову через дійсну , тоді можна переконатись, що амплітудно-фазова характеристика являє собою півколо з центром в точці і з діаметром, рівним k (рис. 3.4, б).

Розподілення точок, які відповідають різним значенням , вздовж кривої залежить від величини сталої часу Т. На графіку показані характерні точки , і .

Вираз для амплітудної частотної характеристики можна одержати за формулами (5.120) або (5.123).

Для розглянутої ланки простіше використати формулу (5.123)

. (3.22)

Графік функції зображений на рис. 3.4, в. З графіка видно, що гармонічні сигнали малої частоти () пропускаються ланкою з відношенням амплітуд вихідної і вхідної величин, близьких до передавального коефіцієнта k. Сигнали великої частоти () погано пропускаються ланкою відношення амплітуд істотно менше від коефіцієнта k. Чим більша стала часу Т, тобто, чим більша інерційність ланки, тим менша характеристика , витягнута вздовж осі частот, або, як прийнято говорити в автоматиці, тим вужча смуга пропускання частот. В практичних розрахунках ширину смуги пропускання ланок і систем визначають за ординатою , рівний . Для інерційної ланки першого порядку

. (3.23)

Графік функції (3.23) показаний на рис. 3.4, г. Чим більша частота вхідного сигналу, тим більше відставання по фазі вихідної величини від вхідної. Максимально можливе відставання рівне 90. При частоті зсув фаз рівний 45.

Розглянута ланка є мінімально-фазовою. Фазовий зсув, який створює ця ланка, менший, ніж в будь-якій іншій ланці з такою ж амплітудною характеристикою. Наприклад, у нестійкій інерційній ланці першого порядку

(3.24)

амплітудна характеристика не відрізняється від характеристики (3.22), а фазова згідно з формулою (5.121) рівна

. (3.25)

При зміні частоти від 0 до + фазовий зсув змінюється від -180 до -90.

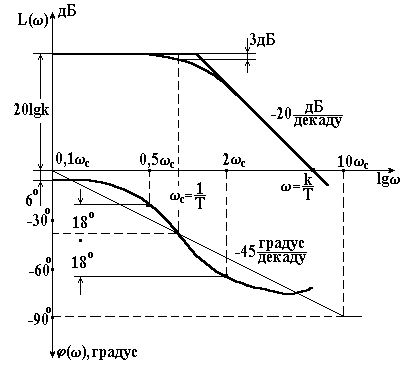
Розглянемо тепер логарифмічні частотні характеристики ланки. Логарифмічна амплітудна характеристика

. (3.26)

Крива, яка точно відповідає функції (3.26), показана на рис. 3.5 тонкою лінією. В практичних розрахунках використовують наближену характеристику , яка являє собою ламану у вигляді двох асимптот.

Перша асимптота (низькочастотна) одержується при малих частотах, коли величиною у виразі (3.26) можна знехтувати і прийняти, що

. (3.27)

Низькочастотна асимптота від частоти не залежить і являє собою пряму, паралельну до осі частот і віддалену від неї на відстань .

Друга асимптота (високочастотна) замінює точну характеристику при великих частотах, коли і одиницю під коренем у формулі (3.26) можна не враховувати. Вираз для цієї асимптоти

. (3.28)

Ця асимптота залежить від частоти. В логарифмічній системі координат вона являє собою пряму, яка має негативний

Рисунок 3.5 – Логарифмічні частотні характеристики інерційної ланки І-го порядку

нахил і проходить через точку з координатами , . Підставляючи у формулу (3.28) два значення частоти і , можна переконатись, що приріст високочастотної асимптоти, яка припадає на одну декаду, рівна – 20 дБ.

Значення спряженої частоти , при якій перетинаються обидві асимптоти, знайдемо з умови

, (3.29)

звідси

. (3.30)

Наближена амплітудна характеристика інерційної ланки першого порядку показана на рис. 3.5 жирною лінією. Можна довести, що найбільша помилка від наближеної заміни одержується при спряженій частоті. Ця помилка рівна 3 дБ.

Фазова частотна характеристика (рис. 3.5, тонка лінія) в системі координат також може бути замінена наближеною характеристикою, яка на інтервалі частот від до являє собою пряму, яка має нахил –45 град./дек. і проходить через точку . Максимальна помилка, яка при цьому допускається, не перевищує 6.

Інерційними ланками першого порядку є конструктивні елементи, які можуть накопичувати енергію і які володіють так званими властивостями самовирівнювання. Найпростішим прикладом такого елемента служить електричний пасивний чотириполюсник (рис. 3.6, а), що складається з резистора опором r, Ом і конденсатора ємністю С, Ф. Вихідна величина чотириполюсника – напруга – після подачі на його вхід постійної напруги змінюється пропорційно величині заряду, що накопичується в ємності. В перші моменти заряд зростає швидко (рис. 3.4, а), а потім в міру наближення на обмотках конденсатора до вхідної напруги струм заряду зменшується, а швидкість зростання напруги поступово спадає до нуля.

Рисунок 3.6 – Приклади інерційних ланок І-го порядку

Параметри передавальної функції (3.18) в чотириполюснику, що розглядається, рівні: , , с.

Властивостями інерційної ланки першого порядку володіють також електричні елементи з індуктивностями L, Г, в яких вихідний сигнал пропорційний струму через індуктивність. Найпростішим прикладом такого роду є ланцюг, зображений на рис. 3.6, б. Передавальний коефіцієнт ланцюга , а стала часу , с.

Більш складним прикладом ланки такого порядку є магнітний підсилювач, який широко використовується в автоматичних системах. На рис. 3.6, в зображена схема найпростішого магнітного підсилювача, так званого дроселя насичення. Його використовують для регулювання струму в ланцюгу активного або пасивного навантаження. Якщо як вхідну величину підсилювача розглядати напругу постійного струму , що подається на обмотку керування, а як вихідну – діюче значення струму в ланцюгу активного навантаження, тоді підсилювач наближено описується передавальної функцією (3.18). Передавальний коефіцієнт підсилювача в такому випадку рівний

, (3.31)

а стала часу

, (3.32)

де – число витків відповідно обмотки керування і робочої обмотки; – опір відповідно обмотки керування, робочої обмотки і навантаження; f – частота напруги мережі.

Магнітні підсилювачі більш складних типів також можуть бути наближено описані передавальною функцією (3.18), але параметри k і Т необхідно визначити експериментально або вирахувати за формулами, які можна знайти в спеціальних довідниках для магнітних підсилювачів.

Приклад. Побудувати амплітудно-фазову характеристику стійкої аперіодичної ланки при значеннях: коефіцієнт підсилення і стала часу ланки .

Підставляючи ці значення в рівняння передавальної функції ланки, одержимо

Зробивши заміну , одержимо рівняння амплітудно-фазової характеристики

Позбавившись уявності в знаменнику, одержимо

Тут дійсна частина

і уявна частина

Для побудови амплітудно-фазової характеристики будемо змінювати частоту від нуля до нескінченності

За одержаними значеннями будуємо апмлітудно-фазову характеристику (рис. 3.7) – півколо, яке проходить через початок координат, який опирається на дійсну вісь, як на діаметр, і розміщений в четвертому квадранті.

Напишемо це рівняння в полярних координатах

Рисунок 3.7 – Амплітудно-фазова характеристика стійкої аперіодичної ланки І-го порядку

Для побудови графіка амплітудно-фазової характеристики будемо змінювати величину від нуля до нескінченності. Знайдемо крайні точки графіка

тобто в цьому випадку ми одержали невизначеність, яку розкриємо, використовуючи правило Лопіталя

Отже,

Одержані точки лежать: одна на осі реальних, а інша – в початку координат і обмежують графік амплітудно-фазової характеристики, яка являє собою півколо з радіусом, рівним , розміщене в четвертому квадранті, що опирається на дійсну вісь, як на діаметр, і проходить через початок координат комплексної площини.

Для перевірки цього припущення досить визначити ординату цього півкола. Абсциса точки центра півкола

Звідки

Підставляючи значення у вираз для ординати точки центра півкола, одержимо

тобто ордината точки центра півкола дійсно рівна його радіусу, що треба було довести.

3.5 Інтегруючі ланки

Розрізняють два види інтегруючих ланок: ідеальні і реальні. Загальною особливістю інтегруючих ланок є пропорційність похідної вихідної величини моментальному значенню вхідної величини. Причому, в ідеальній інтегруючій ланці пропорційність існує в будь-який момент часу після подачі ступінчатої дії, а в реальній – тільки після завершення процесу в ланці.

Диференціальне рівняння ідеальної інтегруючої ланки

. (3.33)

Коефіцієнт пропорційності k залежить від конструктивних параметрів ланки і має розмірність

. (3.34)

Рівнянню (3.33) рівносильне інтегральне співвідношення

, (3.35)

яке в даній формі виражає залежність вихідної величини від вхідної і пояснює назву ланки: ланка інтегрує вхідний сигнал.

Підставляючи у співвідношення (3.34) , можна одержати перехідну функцію

. (3.36)

Графік функції показаний на рис. 3.8, а (лінія 1). Імпульсна перехідна функція ланки

. (3.37)

Передавальна функція ідеальної інтегруючої ланки

. (3.38)

Амплітудно-фазова характеристика ланки

(3.39)

на комплексній площині зображується у вигляді прямої, яка співпадає з уявною віссю (рис. 3.8, б – лінія 1).

Амплітудна частотна характеристика

(3.40)

являє собою гіперболу (рис. 3.8, в, лінія 1), яка при прямує до нескінченності. Цю особливість можна умовно (за аналогом зі статичними ланками) пояснити наявністю передавального коефіцієнта, рівного нескінченості.

При збільшенні частоти значення прямує до нуля. Ця властивість зближує інтегруючі ланки з інерційними.

Рисунок 3.8 – Характеристики інтегруючих ланок

Фазова частотна характеристика ідеальної інтегруючої ланки

(3.41)

показує, що зсув фаз, який породжується ланкою, на всіх частотах однаковий і рівний -90 (рис. 3.8, г, лінія 1).

Логарифмічна амплітудна характеристика

(3.42)

являє собою пряму з нахилом – 20 дБ/дек, яка проходить через точку з координатами

Розглянемо тепер характеристики реальної інтегруючої ланки. Її диференціальне рівняння

, (3.43)

а передавальна функція

. (3.44)

Неважко побачити, що ланка з передавальною функцією (3.43) може розглядатись як послідовне з’єднання двох елементарних ланок: ідеальної інтегруючої з передавальною функцією і статичної інерційної ланки першого порядку зі сталою часу Т і передавальним коефіцієнтом, рівним одиниці. Тому всі частотні характеристики реальної інтегруючої ланки можуть бути одержані за характеристиками цих простих ланок та відповідними правилами перемножування комплексних (векторних) величин.

Характеристики реальної інтегруючої ланки показані на рис. 3.8 (лінія 2).

Інтегруючими ланками є виконуючі двигуни і механізми – прилади, які переміщують виконавчі органи (шибери, заслінки, вентилі і т. д.). Їх називають також серводвигунами і сервомеханізмами. Вхідною величиною цих приладів служить, звичайно, кількість енергії або речовини, яка поступає в прилад, а вихідною – лінійне або кутове переміщення будь-якого елемента. Ступінь ідеальності (безінерційності) таких інтегруючих ланок залежить від величини мас частин, які переміщуються (обертаються) навколо виконавчого приладу і приведеного ним в рух виконавчого органу.

Ідеальною інтегруючою ланкою можна вважати (з деякими припущеннями) гідравлічний виконавчий механізм (рис. 3.9, а), вхідною величиною якого є кількість рідини Q (м3/с), що поступає в одиницю часу в порожнину циліндра, а вихідною – переміщення l (м) поршня з штоком. Дійсно, якщо маса частин, що переміщуються, мала і якщо зусилля, породжене тиском гідронасоса, істотно більше сил опору, то переміщення поршня визначається рівнянням балансу рідини

, (3.45)

де S – площа поршня, м2.

Рисунок 3.9 – Приклади інтегруючих ланок

Рівняння (3.45) легко приводиться до рівняння (3.33) або (3.35). Коефіцієнт k в даному випадку рівний . Його розмірність або 1/м2.

Властивостями ідеальної інтегруючої ланки володіє при деяких умовах інерційна ланка першого порядку. Наприклад, аперіодичний rc-ланцюг при частотах вхідної дії може приблизно розглядатись як інтегруюча ланка. Дійсно, якщо в частотній функції (3.19) знехтувати одиницею в знаменнику, то вона співпадає з функцією (3.39).

Реальними інтегруючими ланками є електричні виконавчі двигуни постійного і змінного струмів. На рис. 3.9, б зображений двофазний асинхронний двигун. Його вхідна величина – напруга змінного струму , прикладена до обмотки керування, вихідна – кут повороту вала , град. Діюче значення напруги на обмотці збудження вважається незмінним. При деяких припущеннях (інерційність обмотки управління мала, статичні механічні характеристики двигуна попередньо лінеаризовані, діапазон зміни напруги обмежений) двигун може бути описаний передавальною функцією (3.44). Передавальний коефіцієнт двигуна приблизно може бути розрахований через номінальні значення частоти обертання , 1/с і керованої напруги

, град./(Вс) . (3.46)

Стала часу залежить від приведеного на вал двигуна моменту інерції частин, що обертаються J, кгм3

, с, (3.47)

де МП – номінальне значення пускового моменту, Нм.

3.6 Диференціююча ланка

Диференціюючою називають таку ланку, в якій вихідна величина пропорційна похідній від вхідної величини

. (3.48)

Перетворимо рівняння (3.48) за Лапласом

тоді

Знаходимо перехідну функцію ланки, перехідна характеристика якої показана на рис. 3.10

Амплітудно-фазова функція

АФХ співпадає з уявною віссю (рис. 3.11).

АЧХ:

ФЧХ:

ЛАЧХ:

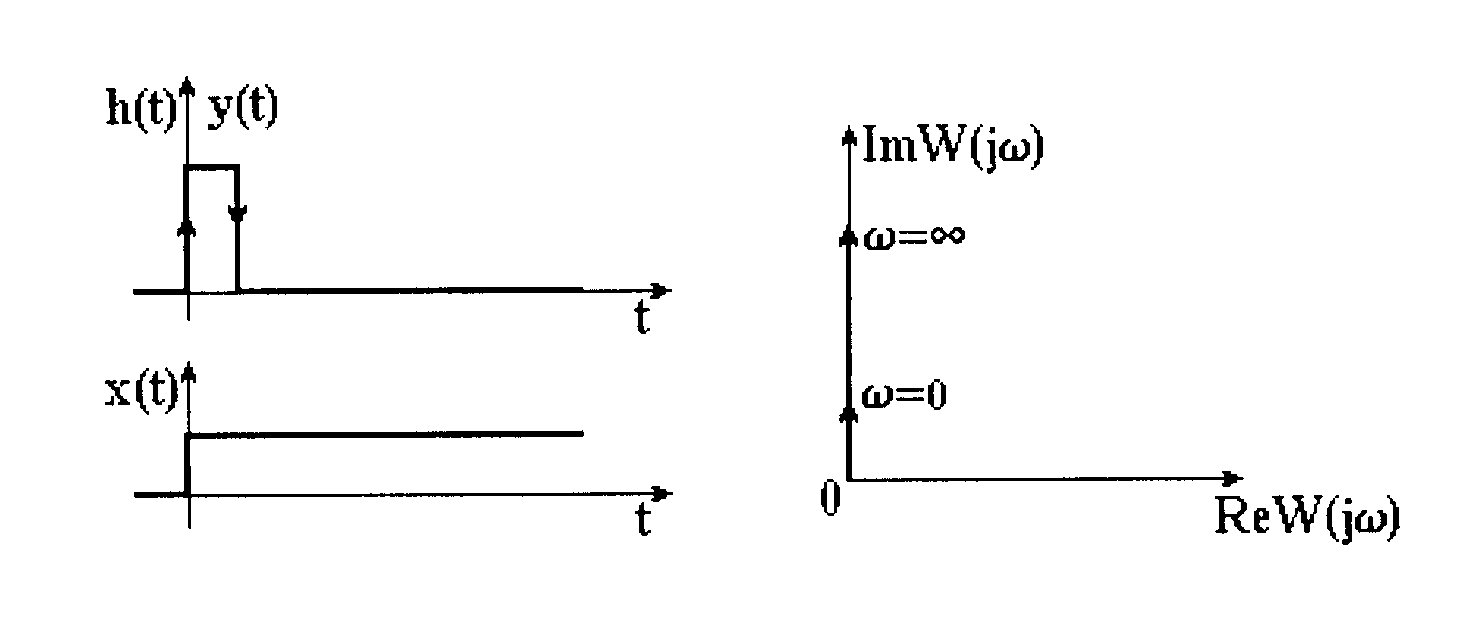
Рисунок 3.10 – Перехідна характеристика диференціюючої ланки

Рисунок 3.11 – АФХ диференціюючої ланки

Реальна диференціююча ланка являє собою послідовне з’єднання ідеальної диференціюючої ланки та інерційної ланки І-го порядку. Вона має таке диференціальне рівняння:

Рисунок 3.12 – АЧХ (а), ФЧХ (б), ЛАЧХ (в) диференціюючої ланки

(3.49)

і передавальну функцію

. (3.50)

Таку ланку можна зобразити у вигляді послідовного або паралельного з’єднання безінерційної і інерційної ланок (рис. 3.13).

Характеристики реальної диференціюючої ланки приведені на рисунку 3.14.

Приклади реальних диференціюючих ланок приведені на рисунку 3.15.

Диференціюючі ланки в статичному режимі не передають сигналу на вихід, вони добре пропускають високочастотні сигнали і погано-низькочастотні. Вони вносять додатковий фазовий зсув.

Рисунок 3.13 – Реальні диференціюючі ланки

Рисунок 3.14 – Характеристики реальної диференціюючої ланки

Рисунок 3.15 – Приклади диференціюючих ланок

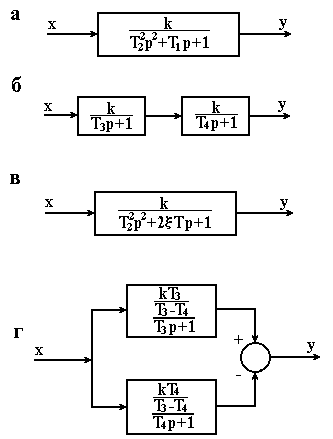
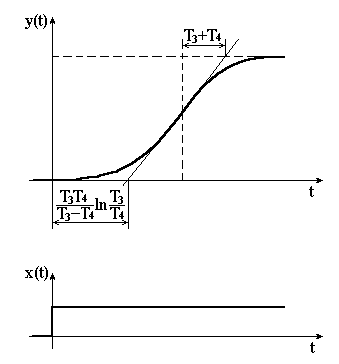
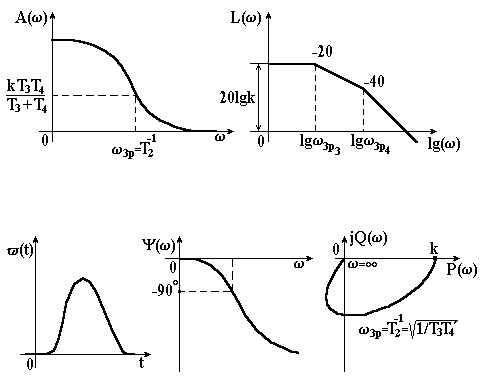
3.7 Інерційні ланки другого порядку

Диференціальне рівняння ланок ІІ-го порядку має вигляд

. (3.51)

Йому відповідає рівняння динаміки в операторній формі

(3.52)

і передавальна функція

. (3.53)

Характеристичне рівняння має два корені

. (3.54)

Характер перехідного процесу залежить від типу коренів, які можуть бути дійсними, комплексними і уявними.

Рисунок 3.16 – Перехідна характеристика аперіодичної ланки
ІІ-го порядку

І. Якщо , то обидва корені дійсні, тобто

де і – умовні постійні часу.

Перехідна характеристика такої ланки є монотонною. Вона близька до інерційної ланки І-го порядку, тому її називають – аперіодична ланка ІІ-го порядку.

При передавальну функцію (3.53) можна представити в таких еквівалентних формах:

, (3.55)

, (3.56)

яким відповідають алгоритмічні схеми, приведені на рисунку 3.17, б, г.

ІІ. Якщо , то корені характеристичного рівняння комплексні і спряжені

(3.57)

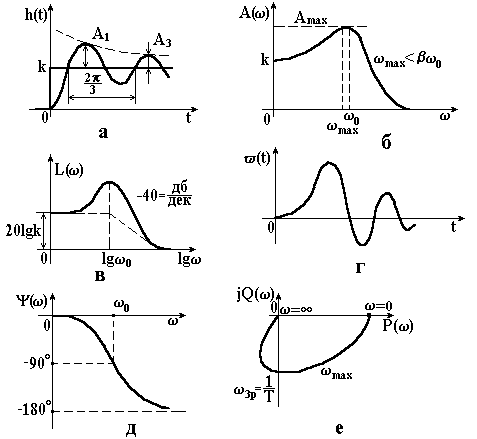
Перехідна характеристика в цьому випадку носить коливальний характер (рис. 3.18). Тобто, маємо коливальну ланку.

ІІІ. Якщо , то обидва корені уявні, і перехідна характеристика являє собою незатухаючу синусоїду. Інерційну ланку ІІ-го порядку з називають ідеальною коливальною або консервативною.

Поряд із загальними властивостями всі ланки реально відрізняються одна від одної. Розглянемо окремо характеристики інерційних ланок ІІ-го порядку.

Перехідна функція аперіодичної ланки ІІ-го порядку може бути одержана додаванням загального рішення

(3.58)

і рішення, яке відповідає примусовій складовій при тоді перехідна функція має такий вигляд:

. (3.59)

Рисунок 3.17 – Алгоритмічні схеми інерційних ланок ІІ-го порядку

Після підстановки початкових умов і у вираз (3.59), маємо

(3.60)


Рисунок 3.18 – Перехідна характеристика коливальної ланки	Рисунок 3.19 – Перехідна характеристика консервативної ланки

тоді перехідна функція має такий вигляд:

. (3.61)

Передавальна функція

. (3.62)

Сталі часу і можна визначити на підставі графікоекспериментальної перехідної характеристики.

Характеристики аперіодичної ланки ІІ-го порядку показані на рис 3.21.

З частотних характеристик даної ланки випливає, що вона добре пропускає сигнали низької частоти і погано пропускає сигнали високої частоти.

Коливальна ланка – це така ланка, в якій при стрибкоподібній зміні вхідної величини вихідна величина прямує до нового встановленого значення, здійснюючи навколо нього затухаючі коливання.

Для більш детального вивчення диференціальне рівняння ланки записують у такому вигляді:

, (3.63)

Рисунок 3.20 – Перехідна характеристика аперіодичної ланки ІІ-го порядку

де – постійна часу, яка характеризує інерційність ланки; де – відносний коефіцієнт затухання; він характеризує коливальність ланки і змінюється від 0 до 1.

Перетворивши рівняння (3.63) за Лапласом, отримаємо передавальну функцію

, (3.64)

. (3.65)

Ця передавальна функція вигідніша, бо тут фігурує одна постійна часу Т. Прирівнюючи до нуля знаменник (3.65), одержимо характеристичне рівняння

Рисунок 3.21 – Характеристики аперіодичної ланки ІІ-го порядку

. (3.66)

Розв’язуючи це рівняння відносно р, будемо мати

, (3.67)

де – коефіцієнт затухання; – кутова частота затухання коливань, рад/с.

Підставляючи в загальний розв’язок диференціального рівняння (3.58) значення комплексних коренів (3.67) і додавши до нього часткове рішення , отримаємо перехідну функцію коливальної ланки

, (3.68)

За допомогою формули Ейлера

(3.69)

функцію (3.68) можна перетворити до такого вигляду:

. (3.70)

Використовуючи початкові умови і 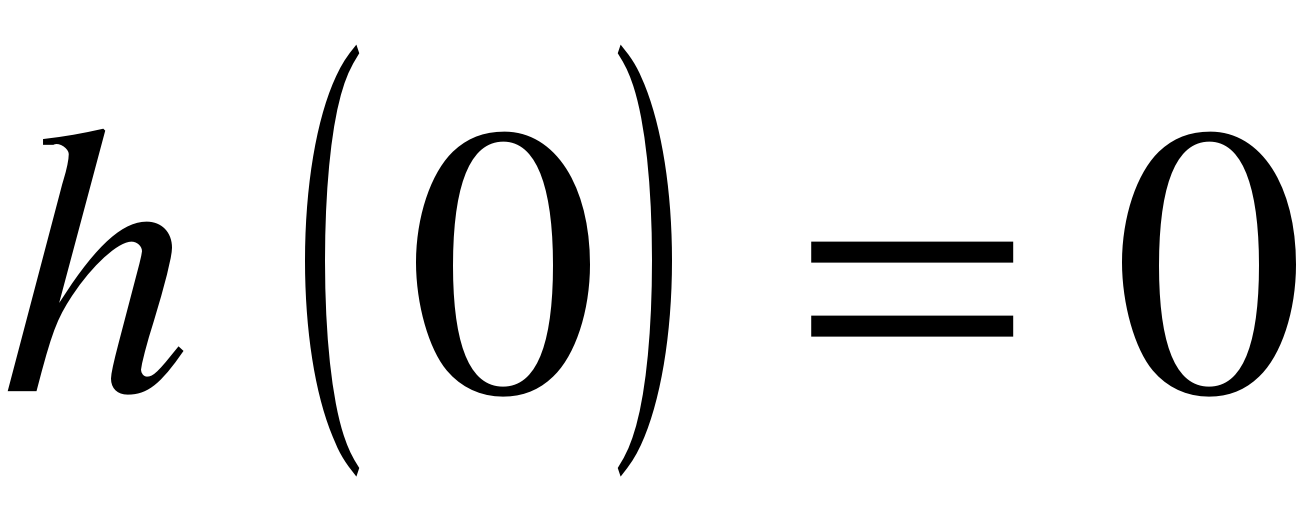, знайдемо

, (3.71)

. (3.72)

Остаточно перехідна функція може бути записана в наступному вигляді:

. (3.73)

Вільна складова перехідної функції (рис. 3.22, а) являє собою синусоїду, амплітуда якої зменшується за законом експоненти.

Період затухаючих коливань дорівнює

. (3.74)

Чим менша постійна часу Т і чим більший коефіцієнт демпфування , тим швидше затухають коливання. Якщо коефіцієнт демпфування , що відповідає , то на виході ланки після подачі одиничного ступінчатого впливу виникають незатухаючі коливання з частотою .

Швидкість затухання коливального перехідного процесу оцінюють степенем затухання

. (3.75)

Чим ближче до одиниці, тим швидше затухають коливання. Степінь затухання залежить від співвідношення дійсної і уявної частин комплексного кореня. Дійсно, якщо у вираз (3.73) підставити два значення t, які відрізняються на період затухання коливань , то можна отримати

. (3.76)

Відношення називають ступенем коливальності.

Використовуючи вираз (3.67), можна з’ясувати зв’язок між ступенем коливальності і коефіцієнтом демпфування

. (3.77)

Від коефіцієнта залежить максимальне значення перехідної функції.

Рисунок 3.22 – Характеристики коливальної ланки ІІ-го порядку

Продиференціювавши (3.70) за t і прирівнявши похідну до нуля, одержимо

, (3.78)

. (3.79)

АФХ коливальної ланки (рис. 3.22, е) описується функцією

. (3.80)

3.8 Ланка запізнення

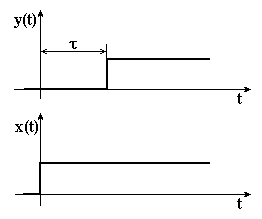
Ланка запізнення – це ланка, вихідна величина якої така сама, як і вхідна, але зсунута на величину чистого запізнення (рис. 3.23).

Передавальну функцію цієї ланки визначають, користуючись виразами для вхідного і вихідного сигналів, перетворених за Фур’є

Тоді АФХ

Отже,

Запишемо передавальну функцію

Якщо ланка запізнення має передавальний коефіцієнт, що відрізняється від одиниці, тобто , то

Рисунок 3.23 – Перехідна характеристика ланки запізнення

Взагалі, запізненням володіють такі ланки, які мають різні властивості. Наприклад: – інерційна ланка І-го порядку.

Такі ланки представляють у вигляді двох послідовно з’єднаних ланок.

Рисунок 3.24 – АФХ (а), АЧХ (б) і ФЧХ (в) ланки запізнення

Рисунок 3.25 – Перехідна характеристика інерційної ланки І-го порядку

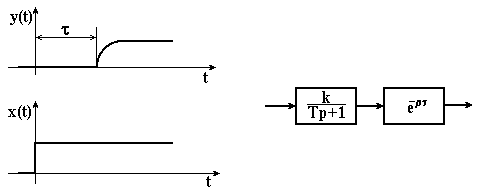
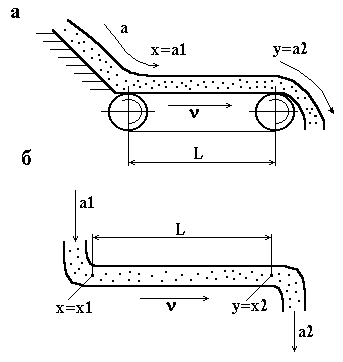
Найбільш характерним прикладом ланки запізнення є: стрічковий живильник (рис. 3.26, а), що транспортує сипкий матеріал (руду, концентрат). Запізнення (с) між кількістю матеріалу (кг/с), який викидається в одиницю часу на живильник матеріалу (кг/с) на спуску живильника залежить від довжини L (м) і швидкості руху v (м/с)

. (3.81)

Другим розповсюдженим прикладом ланки запізнення є трубопровід (рис. 3.26, б), по якому в технічний об’єкт керування рідка речовина (пульпа, розчин реагенту) в кількості (м3/с) з концентрацією корисного компоненту

(кг/м3).

Зазначимо, що необхідність розглядати живильник, трубопровід та інші транспортуючі пристрої як ланки запізнення виникають лише в тих випадках, коли вони є елементами замкнутих автоматичних систем керування.

Таким чином, ланка запізнення відзначається наступними характерними особливостями:

Вона передає будь-які вхідні сигнали без спотворення їх форми, але затримує на інтервалі в сталому режимі (при ) вихідний сигнал.

. (3.82)

Як і для інших статичних (позиційних) ланок, передавальна функція ланки

Рисунок 3.26 – Ланки з запізненням

. (3.83)

За властивостями АЧХ ланка запізнення еквівалентна безінерційній: пропускає високочастотні і низькочастотні сигнали з однаковим відношенням амплітуд (рівним одиниці).
За властивостями ФЧХ вона еквівалентна інерційним ланкам: створює від’ємний зсув (пропорційний запізненню і частоті ).

Типові алгоритмічні ланки, їх частотні та часові характеристики