Классификация измерений

Классификация измерений

Измерения максимально возможной точности, достигаемой при существующем уровне развития науки и техники. Такие измерения проводят при создании эталонов и измерениях физических констант. Характерными для таких измерений являются оценка погрешностей и анализ источников их возникновения.

Технические измерения - это измерения, проводимые в заданных условиях по определенной методике, разработанной и исследованной заранее; как правило, к ним относят массовые измерения, проводимые во всех отраслях народного хозяйства, за исключением научных исследований. При технических измерениях погрешность оценивают по метрологическим характеристикам СИ с учетом при меняемого метода измерения.

Контрольно-поверочные измерения - это измерения, выполняемые службами метрологического надзора с целью определения метрологических характеристик СИ. К таким измерениям относят измерения при метрологической аттестации СИ, экспертные измерения и др.

По способу получения измерения:

• Прямые – когда физическая величина непосредственно связывается с ее мерой;

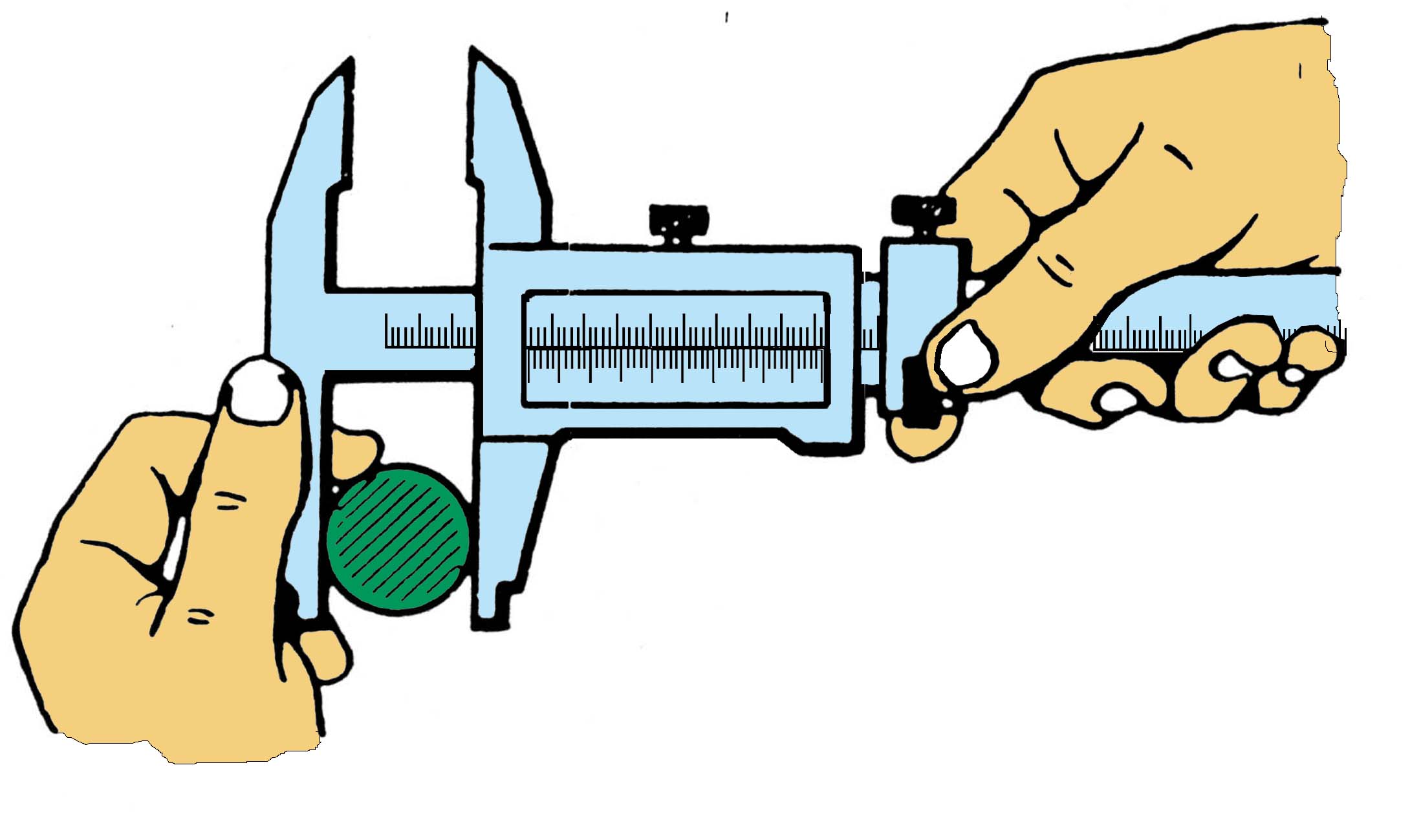
• Косвенные – когда искомое значение измеряемой величины установлено по результатам прямых измерений величин, которые связаны с искомой величиной известной зависимостью;

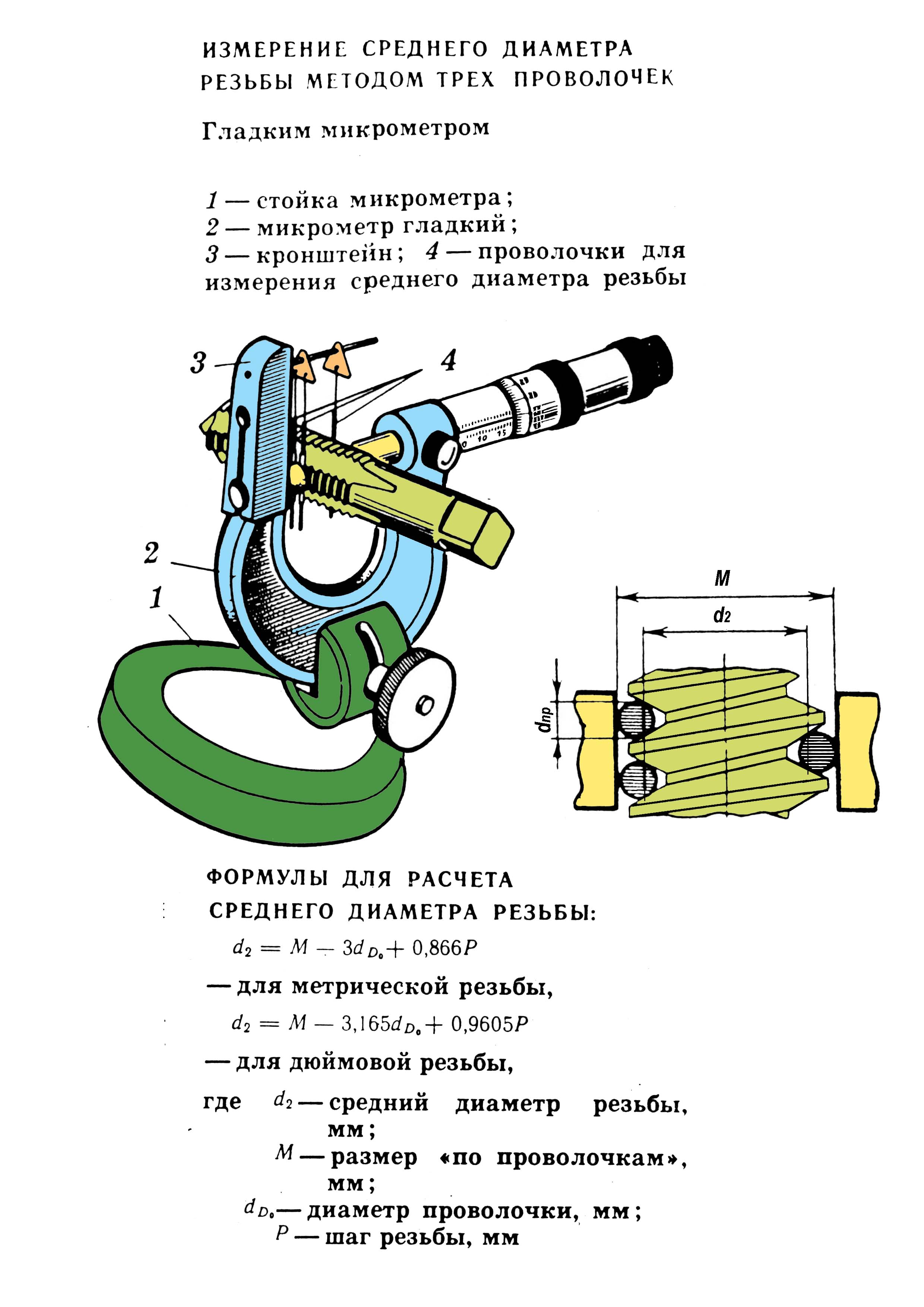
Совокупные – когда используются системы уравнений, составляемых по результатам измерения нескольких однородных величин.

Совокупные измерения - это проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин находят решением системы уравнений, получаемых при прямых измерениях и различных сочетаниях этих величин.

Примером совокупных измерений может служить нахождение сопротивлений двух резисторов по результатам измерений сопротивлений последовательного и параллельного соединений этих резисторов.

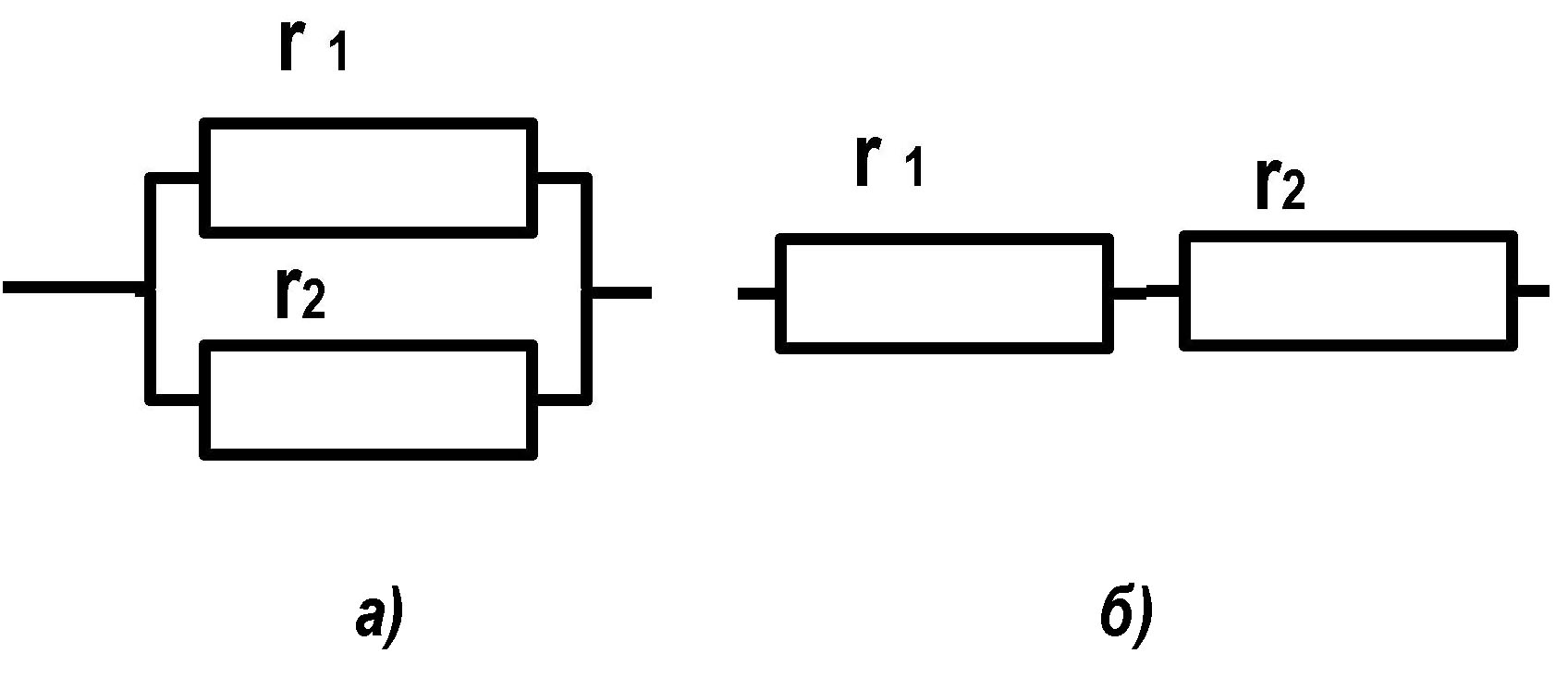
Искомые значения сопротивлений находят из системы двух уравнений.

Совместные измерения - это проводимые одновременно измерения двух или более не одноименных величин для нахождения зависимости между ними

Совместные – производятся с целью установления зависимости между величинами. При этих измерениях определяется сразу несколько показателей. Классическим примером совместных измерений является нахождение зависимости сопротивления резистора от температуры:

R(tO ) = R20 [1 + A(tO - 20) + B(tO - 20)2 ],

Где:

R20 - сопротивление резистора при t = 20 градусов С;

А; В - температурные коэффициенты.

Для получения зависимости R(t) необходимо провести минимум три измерения сопротивления R при трех различных температурах R(t1), R(t2), R(t3), составить систему из трех уравнений и решив ее, определить коэффициенты R20, А, В.

Совместные и совокупные измерения по способам нахождения искомых значений измеряемых величин близки между собой. И в одном, и в другом случае искомые значения находят путем решения систем уравнений. Отличие состоит в том, что при совокупных измерениях одновременно измеряют несколько одноименных величин, а при совместных несколько разноименных

По характеру изменения измеряемой величины:

• Статические – связаны с такими величинами, которые не изменяются на протяжении времени измерения.
• Динамические – связаны с такими величинами, которые в процессе измерений меняются (температура окружающей среды).

По количеству информации:

• Однократные;
• Многократные (> 3);

По отношению к основным единицам измерения:

• Абсолютные (используют прямое измерение одной основной величины и физической константы).
• Относительные – базируются на установлении отношения измеряемой величины, применяемой в качестве единицы. Такая измеряемая величина зависит от используемой единицы измерения

Принцип измерений это совокупность взаимодействия СИ с объектом основанное на физических явлениях.

Метод измерения это совокупность приемов использования принципа и средств измерений.

Все без исключения методы измерений основаны на сравнении измеряемой величины с величиной, воспроизводимой мерой (однозначной или многозначной). При этом в зависимости от способа применения меры известной величины выделяют метод непосредственной оценки и методы сравнения с мерой (см. табл.).

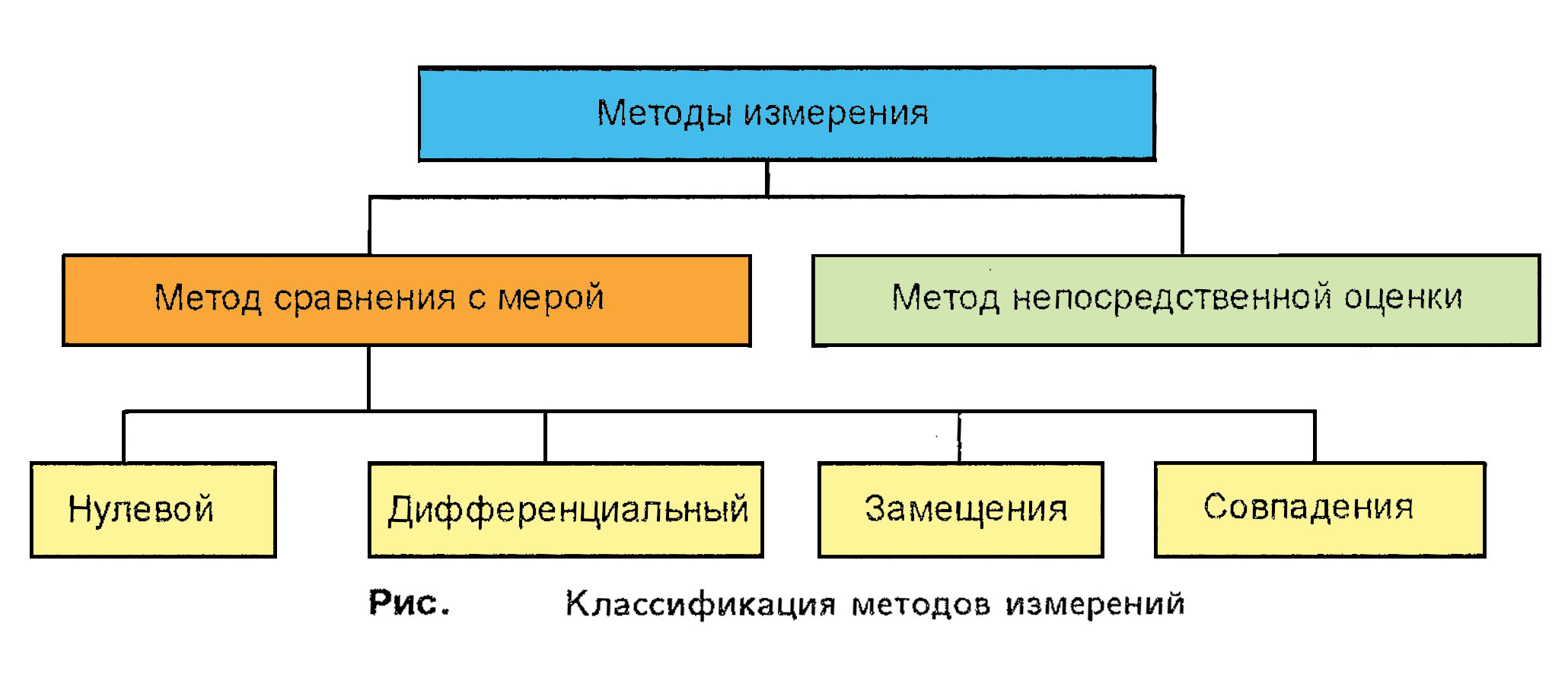
Метод непосредственной оценки - с помощью которого значение величины определяют непосредственно по отсчетному устройству измерительного прибора (измерение длины с применением линейки, массы на пружинных весах, давление - манометром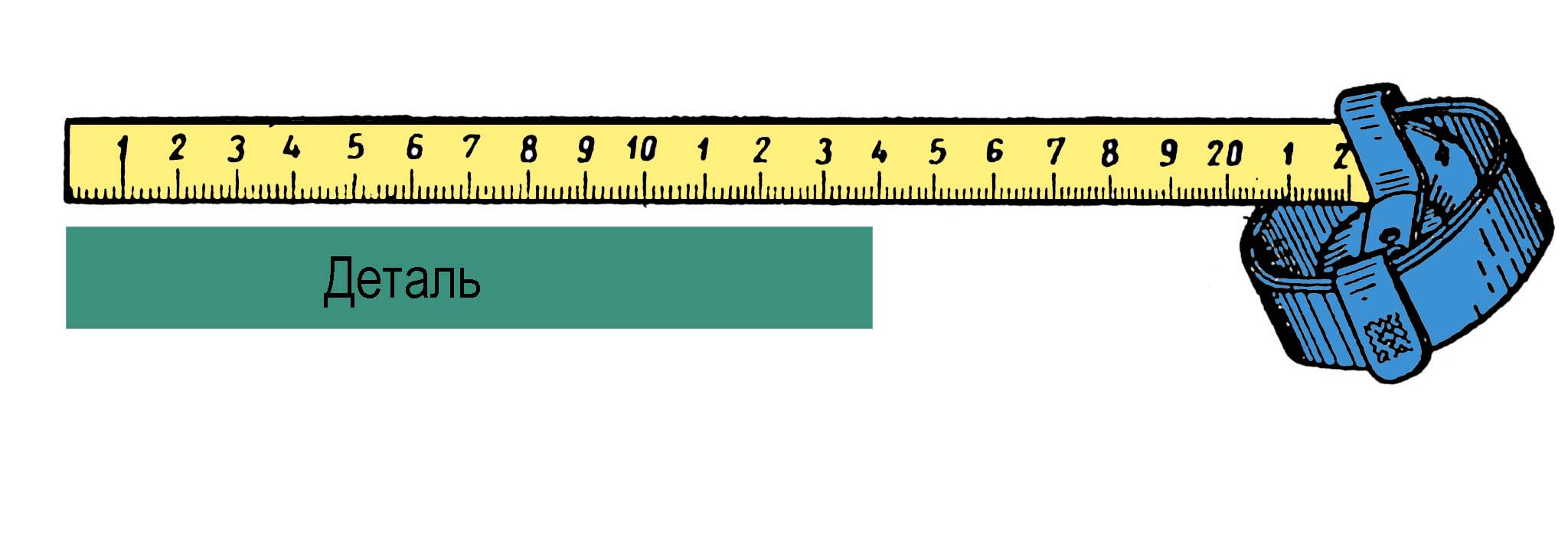

Метод сравнения с мерой - измеряемую величину сравнивают с величиной, воспроизводимой мерой (измерение зазора между деталями с помощью щупа, измерение массы на рычажных весах с использованием гирь и т. п.);

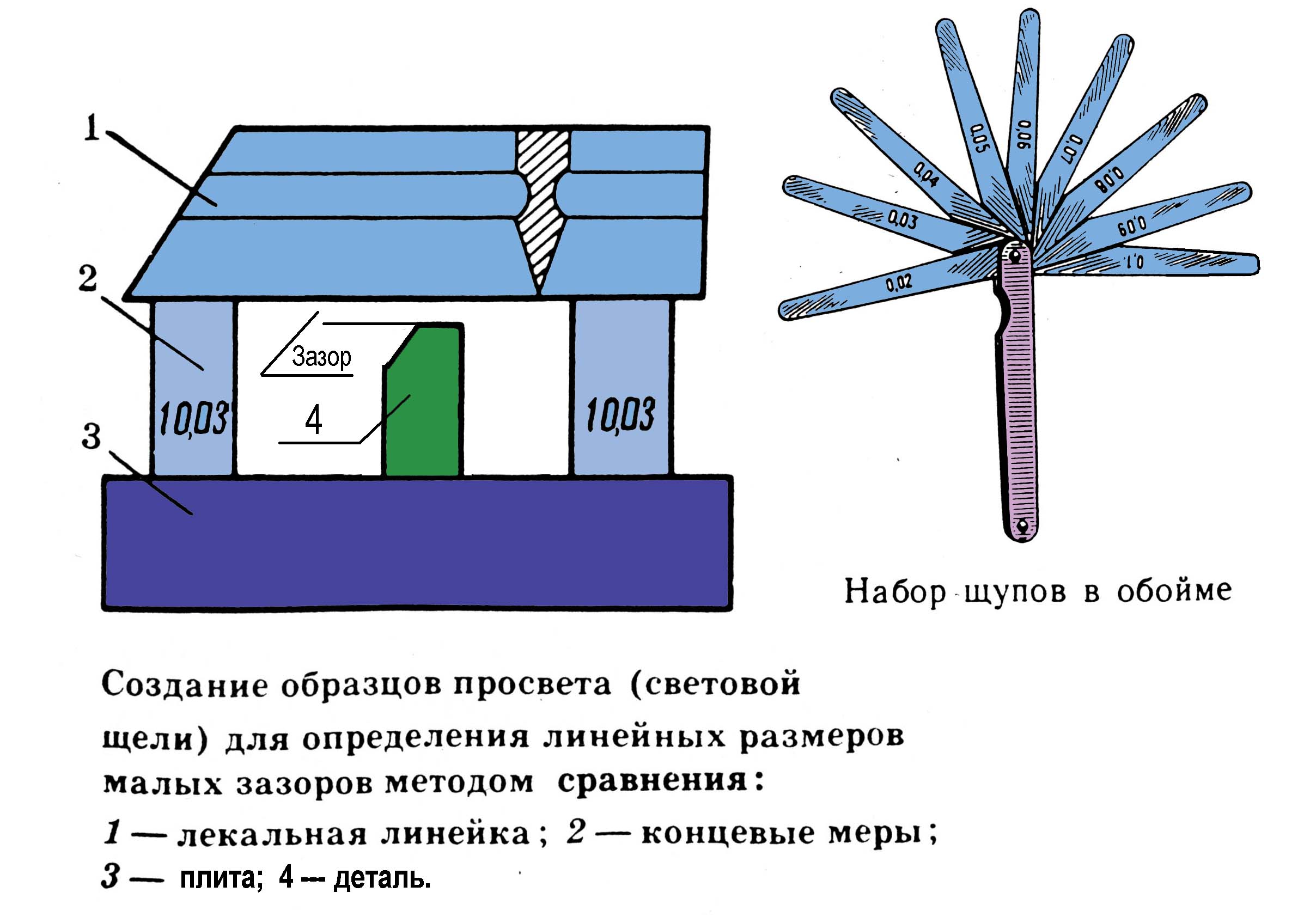
Измерений дополнением - метод сравнения с мерой, при осуществлении которого значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению (измерение массы объекта с помощью рычажных весов, на одну чашку которых помещается объект, а на другую - гири для уравновешивания весов и измерения массы объекта);

Дифференциальный метод - измеряемую величину сравнивают с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и измеряют разность между этими двумя величинами (измерение длины сравнением с образцовой мерой при помощи компаратора - средства сравнения, предназначенного для сличения мер однородных величин);

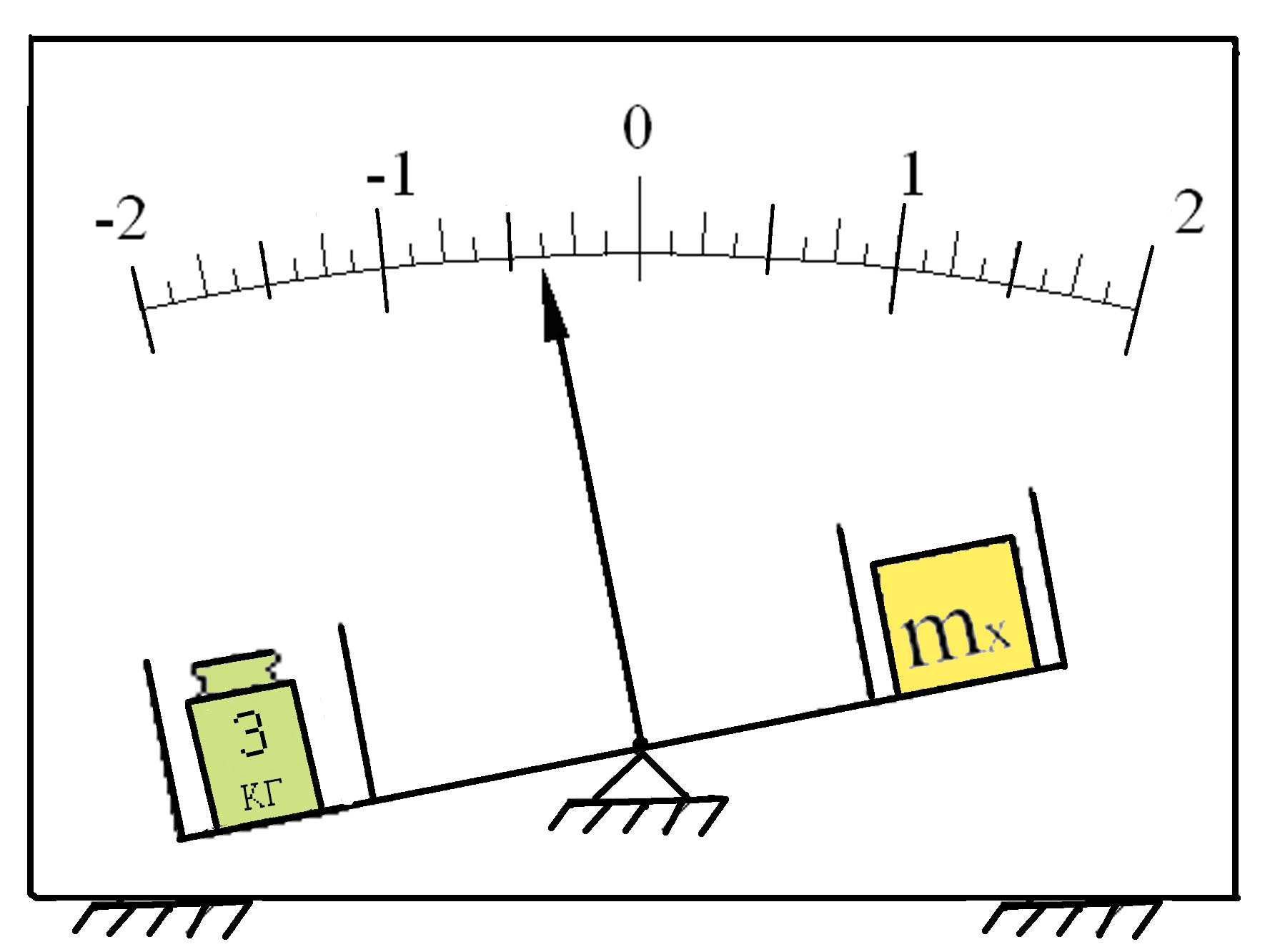
Нулевой метод сравнения с мерой, при реализации которого результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля (измерение электрического сопротивления мостом с полным его уравновешиванием);

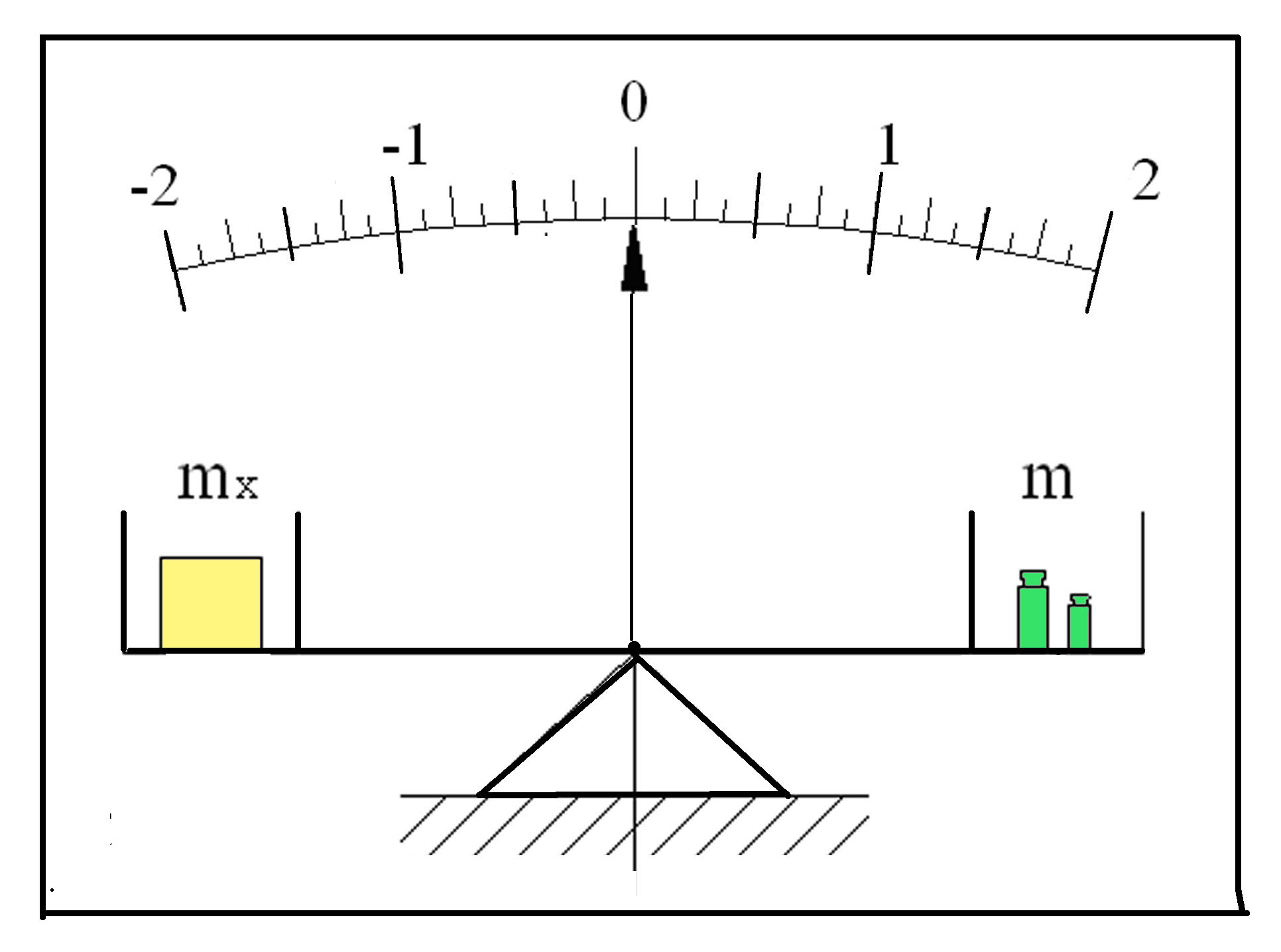
Метод замещения при сравнения с мерой, с помощью которого измеряемую величину замещают мерой с известным значением величины (взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов);

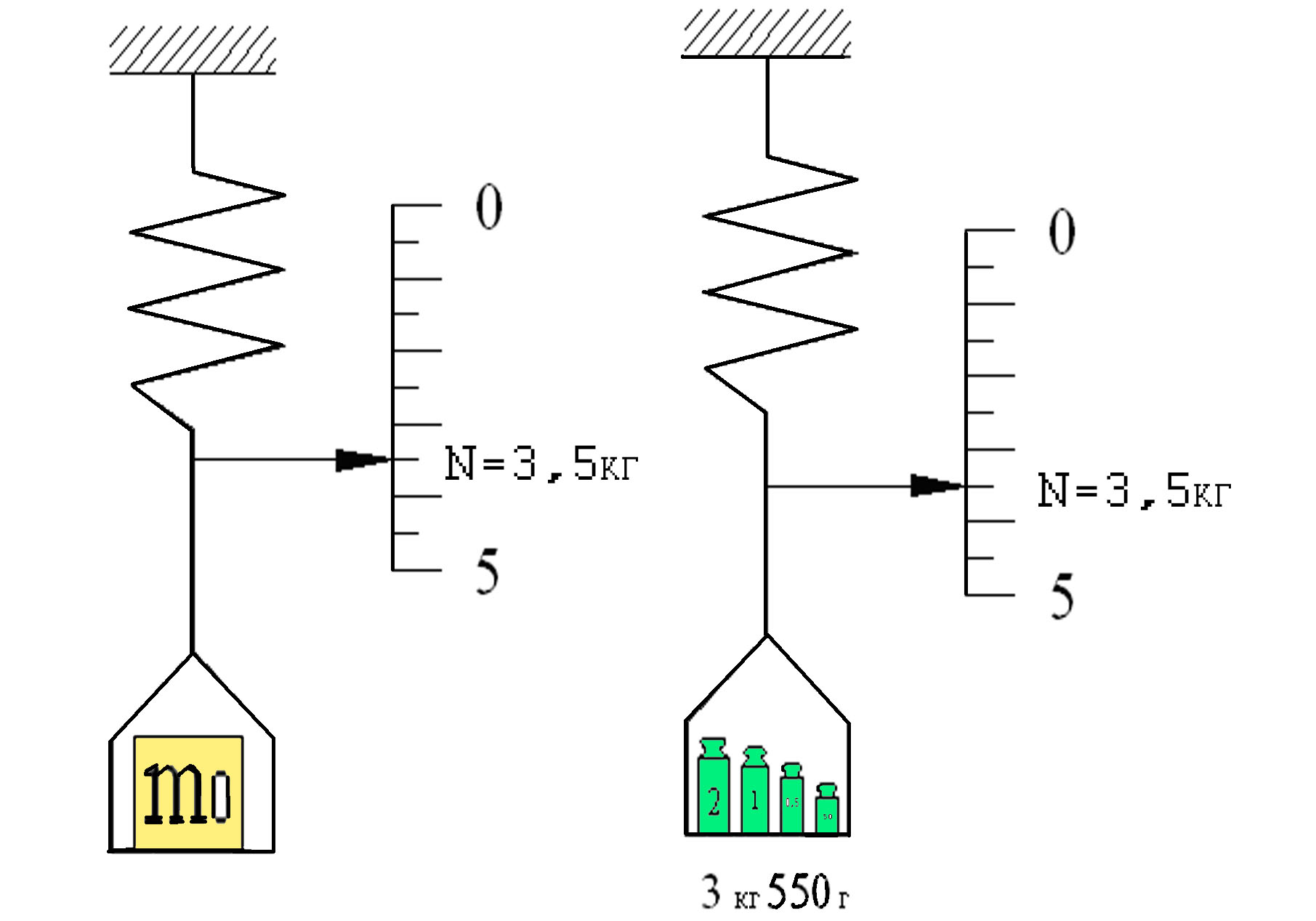
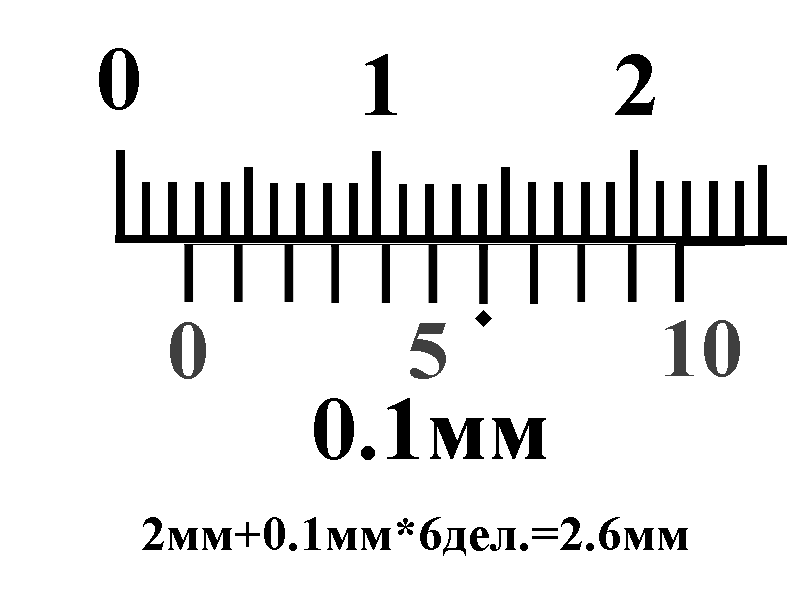
Метод совпадений - сравнения с мерой, при осуществлении которого разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение меток шкал или периодических сигналов (измерение длины с помощью штангенциркуля с нониусом, когда наблюдают совпадение отметок на шкалах штангенциркуля и нониуса; измерение частоты вращения с помощью стробоскопа, когда положение какой-либо отметки на вращающемся объекте совмещают с отметкой на не вращающейся части этого объекта при определенной частоте вспышек стробоскопа).

Различают контактный и бесконтактный методы измерений.

Контактный метод измерений основан на том, что чувствительный элемент прибора приводится в контакт с объектом измерения (определение размеров отверстия штангенциркулем или индикаторным нутромером).

Бесконтактный метод измерений, при котором чувствительный элемент средства измерений не приводится в контакт с объектом измерения (измерение расстояния до объекта с помощью радиолокатора, параметров резьбы - с помощью инструментального микроскопа и др.)

Закономерности формирования результатов измерений

Сходимость результатов измерений

Сходимость результатов измерений - характеристика качества измерений, отражающая близость друг к другу результатов измерений одной и той же величины, выполненных повторно одними и теми же средствами, одним и тем же методом, в одинаковых условиях и с одинаковой тщательностью.

Воспроизводимость измерений

Воспроизводимость результатов измерений - повторяемость (в пределах установленной погрешности) результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами, разными операторами, в разное время, но приведенных к одним и тем же условиям измерений.

Погрешности результатов измерений

Любое измерение производится с некоторой погрешностью, которая искажает результат измерения и позволяет определить лишь приближенное значение· измеряемой· величины. Введение понятия· «погрешность»- требует определения и четкого разграничения понятий истинного и· действительного значений, измеряемой ФВ и результата измерения.

Истинное значение физической величины идеальным образом характеризует в качественном и количественном отношений соответствующую Ф В. Оно не зависит от средств человеческого познания и является той абсолютной истиной, к которой стремятся, пытаясь выразить ее в виде числового значения. Поскольку :«истинное значение»- получить невозможно, то на практике его заменяют-«действительным значением».

Действительное значение физической величины получают экспериментальным путем. Оно настолько близко к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.

Результатом измерения ФВ является ее значение, полученное путем измерения.

Погрешность результата измерения (погрешность измерeнuя) -

это отклонение результата измерения от истинного (действительного) значения измеряемой величины.

На практике при определении погрешности измерения используют действительное значение, в результате чего погрешность измерения определяется по формуле.

где

Dхизм = х - хд

х - результат измерения;

хд - действительное значение измеряемой величины.

Классификация погрешностей измерения по основным признакам приведена в таблице.

В метрологии используют понятия «погрешность измерения»-и «погрешность средств измерений», причем погрешность средств. измерений является одной из составляющих (часто наибольшей) погрешности измерения. Погрешности измерения и погрешности средств измерений по характеру проявления и способу выражения классифицируются одинаково (см. рис. 1).

Рис. 1 Классификация погрешностей средств измерений

По окончании измерения необходимо получить не только значение физической величины, но и оценить точность результата измерения. Количественной мерой точности служат характеристики погрешности результата измерений.

По способу выражения погрешности делят на абсолютные, относительные· и приведенные .

Абсолютную погрешность определяют как разность результата

измерения и действительного значения измеряемой величины:

D = х - хд

Т.е. это погрешность измерения, выраженная в единицах измеряемой величины.

Абсолютная погрешность ·независима от измеряемой величины, поэтому она не может в полной мере служить показателем точности измерений ФВ, в частности различных размеров.

Например, погрешность измерения А =0,001 мм при измерении длины L -100 мм соответствует достаточно высокой точности измерений, а при L -1мм - низкой.

Относительная погрешность выражается отношением абсолютной погрешности измерения к действительному или истинному значению измеряемой. величины. Относительную погрешность в долях или процентах находят из отношений:

dх = (А / х) или dх = (А / х) 100%.

Тогда из предыдущего измерении длины L= 100 мм, Dх= (0,01/100) ·100% = 0,01% , а при L = 1 мм = (0,01/1) 100%=1% .

Относительная погрешность является наиболее информативной, так как дает возможность объективно сопоставлять результаты и оценивать качество измерений, выполненных в разное время, различными средствами или операторами, а также ранжировать погрешности измеряемой величины с различными размерностями и числовыми значениями.

Однако относительная погрешность измерения не может быть использована для нормирования погрешности некоторых средств измерений (например, электроизмерительных приборов), поскольку при приближении измеряемой величины к нулю незначительные ее изменения приводят к громадным изменениям Dх..

Исключение указанного недостатка возможно при нормировании по приведенной погрешности измерения.

Приведённой называется относительная погрешность g, выраженная в процентах от некоторого нормирующего значения х н

g= ± (D / х н) . 100%.

Часто за нормирующее значение - х н принимают верхний предел измерений средств измерений, т.е. х н= х max .

По характеру проявления погрешности делятся на систематические, случайные и промахи.

Систематическая погрешность измерения - это составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же ФВ.

Отличительной особенностью систематических погрешностей является предсказуемость их поведения. Они могут быть почти полностью устранены путем введения соответствующих поправок. К систематическим постоянным погрешностям (остающимся постоянными при повторных измерениях) можно отнести погрешности от несоответствия действительного значения меры, с помощью которой выполняют измерения, ее номинальному значению, а также погрешности, вызванные температурной деформацией измеряемой детали или средства измерений при отклонении температуры от нормальной области значений.

Примером систематической переменной погрешности, закономерно изменяющейся при повторных измерениях одной и той же ФВ (рис….), является погрешность, вызванная, например, износом измерительного наконечника средства измерений при контактных измерениях.

Случайная погрешность измерения - это составляющая погрешности результата измерения, изменяющаяся случайным образом при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же ФВ.

В проявлении этих погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения.

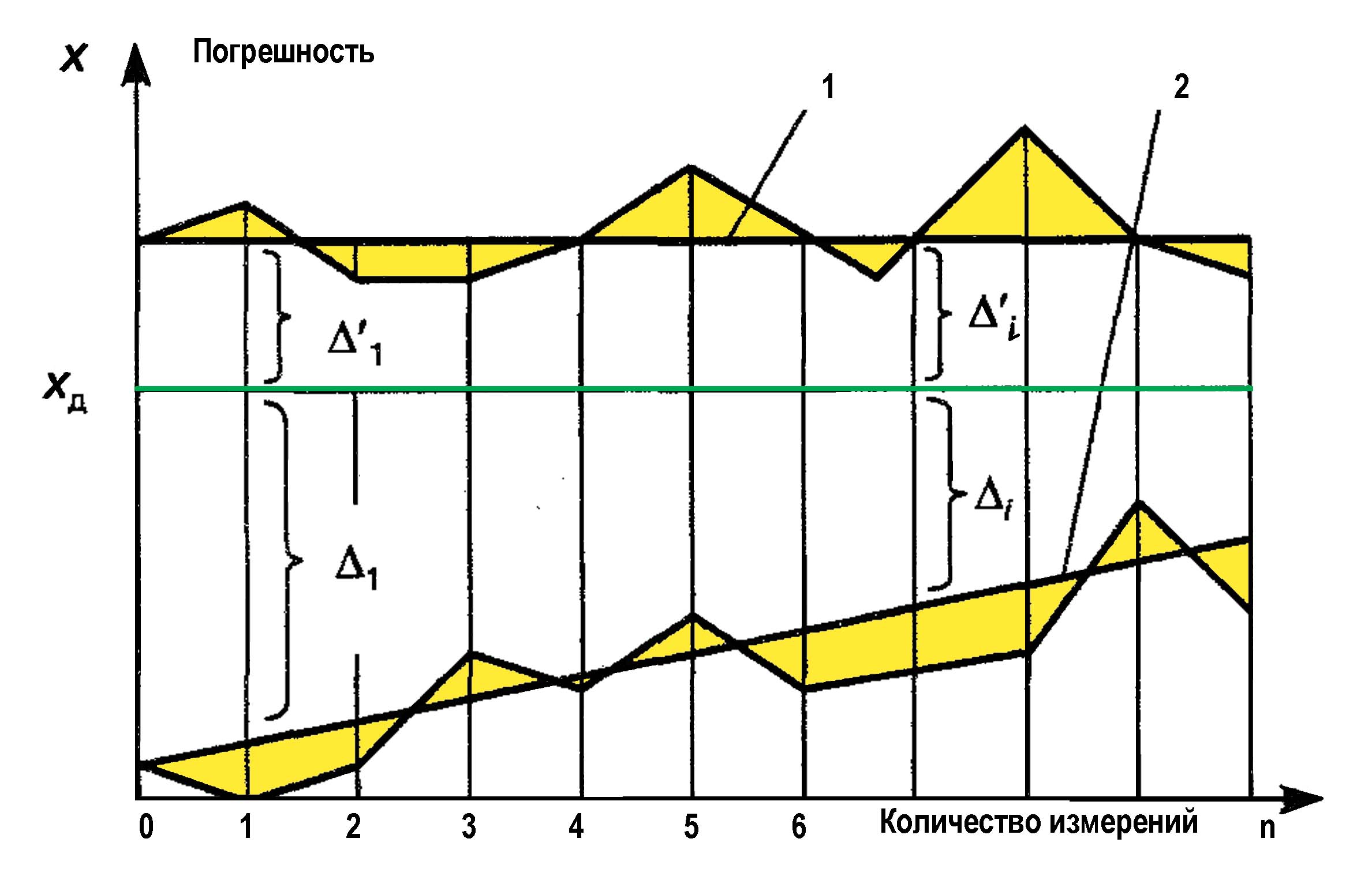
Рис. 3. Систематические погрешность

1 - постоянная; 2 - переменная; п - номер повторяемого измерения;

и - систематические погрешности i-го измерения ;

= = ... = = const, т.е. = const

... const, т.е. const

В отличие от систематических случайные погрешности нельзя исключить из результата измерения путем введения поправок, однако их можно существенно уменьшить путем увеличения числа единичных измерений. Причин, вызывающих случайные погрешности, множество, например перекосы элементов прибора, нерегулярные изменения моментов трения в. опорах, колебания температуры окружающей среды, округления показаний прибора, изменение внимания оператора и др.

К случайной погрешности результата измерения относится также промах или грубая погрешность.

Промах (грубая погрешность) - это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.

Промахи, как правило, возникают из-за ошибок или неправильного действия оператора, кратковременных резких изменений условий проведения измерений и др. Если промахи обнаруживаются в процессе измерений, то результаты, их содержащие, отбрасывают как недостоверные. Как правило, выявление промахов производится на основании анализа результатов измерений с помощью различных вероятностных критериев.

Обязательными компонентами любого измерения являются средства измерений, метод измерения и оператор, проводящий измерения. В связи с этим по источнику возникновения различают инструментальные, методические и субъективные погрешности.

Инструментальная погрешность измерения - это составляющая погрешности измерений, обусловленная погрешностью применяемого средства измерений.

Методическая погрешность измерения (погрешность метода измерения) - это составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений. Такая погрешность возникает вследствие: ограниченной точности расчетных формул, положенных в основу измерений; влияния приема использования средства измерений; экстраполяций значения свойства, измеренного на ограниченной части объекта, на весь объект и др. В большинстве случаев методические погрешности носят систематический характер, однако возможно и случайное их проявление. Например, если уравнения метода измерений включают в себя коэффициенты, зависящие от условий измерений, которые меняются случайным образом.

Субъективная погрешность измерения - это часть погрешности измерения, зависящая от оператора. Она обусловлена погрешностью отсчитывания оператором показаний, влиянием теплоизлучения оператора на средство измерений и погрешностями, связанными с квалификацией оператора.

При изготовлении изделий машиностроения значительная часть про водимых измерений приходится на долю измерений геометрических параметров деталей: линейных и угловых размеров, отклонений формы и расположения поверхностей, шероховатости, параметров точности резьб, зубчатых колес и др. В связи с этим рассмотрим более подробно формирование погрешностей измерения геометрических параметров деталей.

Погрешность измерения геометрических параметров деталей с учетом условий и метода измерений можно рассчитать по формуле ;

где:

D1 - погрешность средства измерений

D2 - погрешность метода измерений

D3 - погрешность от температурных деформаций средства измерений

D4 - субъективная погрешность оператора

D5 - погрешность от измерительного усилия

D6 - другие погрешность средства измерений кроме указанных

Исключение систематических погрешностей

Известные систематические погрешности можно исключить, либо за счет устранения источников погрешностей до начала измерений (профилактика погрешностей), либо путем введения известных поправок в результат измерения в процессе измерения. Профилактика погрешностей является наиболее рациональным способом их снижения. Профилактику погрешностей измерения производят путем регулировки, ремонта и поверки средств измерений. Снизить погрешность измерения можно, устранив влияние колебания температуры (например, термоизоляцией), вибраций и т.п.

Поправка - это значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности. Путем введения поправки исключают, как правило, систематическую постоянную погрешность средств измерений.

При введении поправки уравнение измерения будет иметь вид

y=x+c+n,

где x - значение измеряемой величины;

c - систематическая погрешность измерения;

n - поправка.

Поправка численно равна значению систематической погрешности и противоположна ей по знаку n = - c

Полученное при измерении значение величины и уточненное путем введения в него необходимых поправок на действие систематических погрешностей называют исправленным результатом измерения. Неисправленный результат измерения - значение величины, полученное при измерении до введения в него поправок.

Одним из наиболее распространенных методов исключения систематических погрешностей в процессе измерения является метод замещения.

Для реализации этого метода сначала измеряют неизвестную величину (объект измерения размером х), в результате чего получают

хси=х+с,

где хси - показания средства измерений.

Ничего не меняя в измерительной системе, устанавливают вместо объекта измерения размером х регулируемую меру (либо меру из набора) с размером хм, подбирая такое ее значение, при котором достигается прежнее показание средства измерений, тогда

хси= хм+c

Сопоставляя равенства получают значение неизвестной величины при х = хм и определяют значение систематической погрешности

с=хси-хм

Пример При измерении диаметра цилиндрической детали штангенциркулем ШЦ-II-0,05 получен результат хси = 25,75 мм.

Определить поправку, которую необходимо внести в показания прибора, используя набор плоскопараллельных концевых мер длины.

Такой же результат (25,75мм) получают при измерении штангенциркулем блока концевых мер размером хм = 25,65 мм. Тогда х = 25,65 мм;

а систематическая погрешность штангенциркуля составит, мм:

с = 25,75 - 25,65 = 0,1мм.

Таким образом, поправка, которую необходимо ввести в показания штангенциркуля, мм:

n = -с = -0,1мм.

Универсальным методом исключения неизвестных постоянных систематических погрешностей является метод рандомизации. Суть этого метода заключается в том, что одна и та же величина измеряется различными методами (приборами). Систематические погрешности каждого из них для всей совокупности являются различными случайными величинами. Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности взаимно компенсируются.

Одним из наиболее простых способов обнаружения и устранения переменных систематических погрешностей является графический метод, который заключается в построении графика последовательности неисправленных значений результатов единичных измерений. Расположение полученных точек позволяет обнаружить наличие закономерного изменения результатов измерений и сделать вывод о присутствии в них систематической погрешности.

На рисунке представлено несколько однократных измерений постоянной величины х0, выполненных через равные промежутки времени. Если закон изменения систематической погрешности близок к линейному, то графический метод обеспечивает практически полное ее исключение.

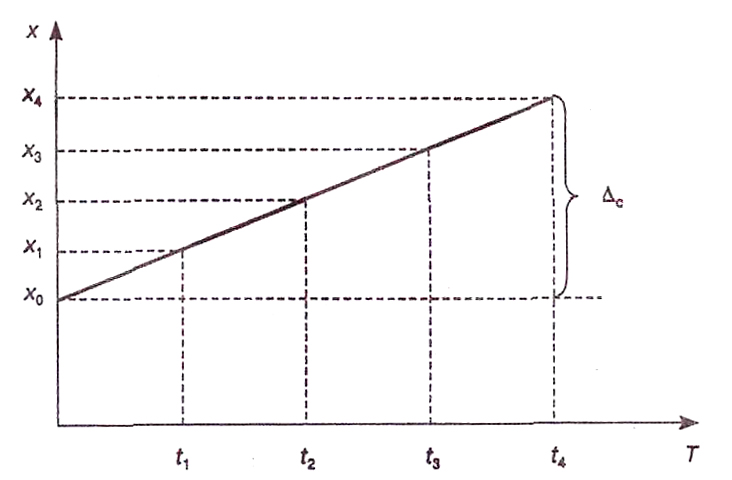
Линейное изменение систематической погрешности

Исключение промахов

Если заранее известно, что какой-либо результат измерения получен из-за грубой ошибки при проведении измерений (неверный отсчет или запись показаний, сбой показаний прибора и т.п.), этот результат считается промахом и его следует исключить из рассматриваемой совокупности результатов измерений, не подвергая никаким проверкам.

Если же имеется сомнение, то каждый из промахов подлежит статистической проверке. Существует несколько критериев для оценки промахов.

Если число измерений n 20 и распределение результатов измерений подчиняется нормальному закону, используют критерий «тpex сигм». По этому критерию считается, что результат хi возникший с вероятностью

Р 0,003 (0,3%), маловероятен и его логично считать промахом при

При числе измерений n < 20 целесообразно применять критерий Романовского. При этом вычисляют отношение

где - результат, вызывающий сомнение;

- коэффициент, предельное значение которого (табличное) определяют по табл.

Значения

Уровень значимости q	Число измерений
	n=4	n=6	n=8	n=10	n=12	n=14	n=16
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,69	2,78
0,10	1,69	2,00	2,17	2,29	2,39	2,49	2,62

При результат измерения хi исключают («отбрасывают»), так как этот результат является промахом.

Если число измерений невелико (n 10), то можно использовать критерий Шовине. В этом случаи считают, что результат xi является промахом, если превышает значения, приведенные далее:

>	1,6	при	n=3
	1,7	при	n=6
	1,9	при	n=8
	2,0	при	n=10

Пример. При измерении диаметра вала микрометром были получены значения. Определить, имеется ли среди результатов промах.

Измерение микрометром размера вала мм
№	1	2	3	4	5	6	7	8	9	10	11	12
И	14,24	14,26	14,28	14,28	14,31	14,34	14,40	14,41	14,42	14,42	14,45	14,80
№	13	14	15	16	17	18	19	20	21	22	23	24
И	14,34	14,40	14,41	14,42	14,42	14,28	14,28	14,31	14,34	14,26	14,28	14,31

Так как n > 20, для определения промахов используем критерий «трёх сигм».

Сравнивая разницу с уровнем получим:

=14,36-14,24=0,12

=0,33

0,12<0,33 ,

следовательно, х1 не является промахом.

Проведя анализ и других измерений, приходим к выводу, что промахом является измерение номер 12:

=14,36-14,80=0,44

0,44>0,33

Пример . При измерении диаметра вала микрометром были получены значения:

Измерение микрометром размера вала мм
№	1	2	3	4	5	6	7	8	9	10	11	12
И	12,24	12,26	12,28	12,28	12,31	12,34	12,40	12,41	12,42	12,42	12,45	12,80

Число измерений n =12. Определить, является ли последний результат x12= 12,80 мм промахом при Р = 0,95 (q = 1 - Р = 0,05).

Так как n < 20, для определения промахов используем критерий Романовского.

Для n = 12 и q = 0,05 = 2,52 (см. табл. …), т.е, и результат хi=x12= 12,80 мм необходимо отбросить, так как он является промахом.

Пример. При измерении диаметра вала микрометром были получены значения:

Измерение микрометром размера вала мм
№	1	2	3	4	5	6
И	30,12	30,27	30,28	30,29	30,32	30,38

Число измерений n = 6. Определить, является ли первый результат x1=30,12 мм промахом.

Так как n < 10, для определения промахов используем критерий Шовине.

что больше, чем 1,7 = 0,1462 мм. Следовательно, причиной появления результата xi=x1=30,12 мм является промах и этот результат необходимо исключить из полученного ряда результатов измерений.

Многократные прямые измерения

Основная задача обработки многократных измерений, заключается в нахождении результата измерения ФВ и доверительного интервала, в котором находится ее истинное (действительное) значение.

Исходной информацией для обработки является ряд из n (n > 4) результатов единичных измерений x1, x2, ..., xn, из которых исключены известные систематические погрешности. Число измерений зависит от требований к точности получаемого результата и от реальной возможности выполнения повторных измерений.

Последовательность обработки результатов многократных измерений включает в себя ряд этапов:

1) исключение из результатов измерений известных систематических погрешностей;

2) вычисление среднего арифметического значения измеряемой величины из n единичных результатов;

3) вычисление средней квадратической погрешности единичных измерений в ряду измерений ;

4) исключение промахов (грубых погрешностей измерений);

5) вычисление средней квадратической погрешности результата измерений среднего арифметического ;

6) проверку гипотезы о принадлежности результатов измерений нормальному закону;

7) вычисление доверительных границ случайной погрешности измерений ±;

8) вычисление доверительных границ неисключенной систематической погрешности результата измерений ±;

9) вычисление доверительных границ погрешности результата измерений ±;

10) представление результата измерения в виде , где P - доверительная вероятность.

Известные систематические погрешности исключают введением в результат измерений соответствующих поправок, численно равных систематическим погрешностям, но противоположным им по знаку. Поправку вводят в результаты единичных измерений, а если известно, что результаты всех единичных измерений имеют одинаковые систематические погрешности, ее исключают из среднего арифметического значения измеряемой величины.

Среднее арифметическое значение измеряемой величины из n

единичных результатов рассчитывают по формуле

Для определения средней квадратической погрешности (СКП) единичных измерений в ряду измерений используют формулу

Промахи (грубые погрешности) могут сильно исказить результат измерений, поэтому их исключение из ряда измерений обязательно.

Среднюю квадратическую погрешность результата измерений (СКПр)

среднего арифметического значения вычисляют по формуле

Гипотезу о принадлежности результатов измерений нормальному закону проверяют с помощью специальных критериев, если число измерений n > 50; составной критерий используют, если 15 < n < 50. При n 15 гипотезу о нормальном законе распределения результатов измерений не проверяют, предполагая, что вид закона распределения известен заранее. Это, как правило, нормальный закон распределения.

При заданном значении доверительной вероятности Р и числе единичных измерений n по таблицам функций определяют значения параметров.

Рассмотрим определение доверительного интервала результата измерений при отсутствии систематической погрешности.

Вероятность того, что истинное значение x измеряемой величины находится в пределах от xн до xв

,

где q - уровень значимости.

Здесь Р называют доверительной вероятностью, а интервал от хн до хв - доверительным интервалом результата измерений.

Будем полагать, что значение случайной величины х подчиняется нормальному закону распределения, то доверительный интервал симметричен относительно точечной оценки и определяется из таблиц значений интегральной функции Лапласа :

, ,

где - аргумент функции Лапласа, отвечающий вероятности Р/2.

- доверительные границы погрешности результата измерений.

Полученный доверительный интервал определяется по формуле

Вычисление доверительных границ производится, как правило, с доверительной вероятностью Р = 0,90; 0,95 или 0,99.

Пример. Выполнено 45 единичных измерений линейного размера детали с помощью индикатора часового типа, установленного на стойке. Получены следующие исправленные результаты измерений:

= 19,95 мм, = 0,13 мм. Определить доверительный интервал результата измерений, если закон распределения - нормальный, а доверительная вероятность Р = 0,95.

1. По формуле найдем СКП результата измерений среднего арифметического, мм:

2. По таблице, значений функции Лапласа

Значение интеграла Таблица

z	Ф(z)	z	Ф(z)	z	Ф(z)
0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 0,37 0,38 0,39 0,40 0,41	0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0,0753 0,0793 0,0832 0,0871 0,0910 0,0948 0,0987 0,1026 0,1064 0,1103 0,1141 0,1179 0,1217 0,1255 0,1293 0,1331 0,1368 0,1406 0,1443 0,1480 0,1517 0,1554 0,1591	0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 0,50 0,51 0,52 0,53 0,54 0,55 0,56 0,57 0,58 0,59 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67 0,68 0,69 0,70 0,71 0,72 0,73 0,74 0,75 0,76 0,77 0,78 0,79 0,80 0,81 0,82 0,83	0,1628 0,1664 0,1700 0,1736 0,1772 0,1808 0,1844 0,1879 0,1915 0,1950 0,1985 0,2019 0,2054 0,2088 0,2123 0,2157 0,2190 0,2224 0,2257 0,2291 0,2324 0,2357 0,2389 0,2422 0,2454 0,2486 0,2517 0,2549 0,2580 0,2611 0,2642 0,2673 0,2703 0,2734 0,2764 0,2794 0,2823 0,2852 0,2881 0,2910 0,2939 0,2967	0,84 0,85 0,86 0,87 0,88 0,89 0,90 0,91 0,92 0,93 0,94 0,95 0,96 0,97 0,98 0,99 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 1,25	0,2995 0,3023 0,3051 0,3078 0,3106 0,3133 0,3159 0,3186 0,3212 0,3238 0,3264 0,3289 0,3315 0,3340 0,3365 0,3389 0,3413 0,3438 0,3461 0,3485 0,3508 0,3531 0,3554 0,3577 0,3599 0,3621 0,3643 0,3665 0,3686 0,3708 0,3729 0,3794 0,3770 0,3790 0,3810 0,3830 0,3849 0,3869 0,3888 0,3907 0,3925 0,3944

z	Ф(z)	z	Ф(z)	z	Ф(z)
1,26 1,27 1,28 1,29 1,30 1,31 1,32 1,33 1,34 1,35 1,36 1,37 1,38 1,39 1,40 1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49 1,50 1,51 1,52 1,53 1,54 1,55 1,56 1,57 1,58 1,59 1,60 1,61 1,62 1,63 1,64 1,65 1,66 1,67 1,68 1,69	0,3962 0,3980 0,3997 0,4015 0,4032 0,4049 0,4066 0,4082 0,4099 0,4115 0,4131 0,4147 0,4162 0,4177 0,4192 0,4207 0,4222 0,4236 0,4251 0,4265 0,4279 0, 4292 0,4306 0,4319 0,4332 0,4345 0,4357 0,4370 0,4382 0,4394 0,4406 0,4418 0,4429 0,4441 0,4452 0,4463 0,4474 0,4484 0,4495 0,4505 0,4515 0,4525 0,4535 0,4545	1,70 1,71 1,72 1,73 1,74 1,75 1,76 1,77 1,78 1,79 1,80 1,81 1,82 1,83 1,84 1,85 1,86 1,87 1,88 1,89 1,90 1,91 1,92 1,93 1,94 1,95 1,96 1,97 1,98 1,99 2,00 2,02 2,04 2,06 2,08 2,10 2,12 2,14 2,16 2,18 2,20 2,22 2,24 2,26	0,4554 0,4561 0,4573 0,4582 0,4591 0,4599 0,4608 0,4616 0,4625 0,4633 0,4641 0,4649 0,4656 0,4664 0,4671 0,4678 0,4686 0,4693 0,4699 0,4706 0,4713 0,4719 0,4726 0,4732 0,4738 0,4744 0,4750 0,4756 0,4761 0,4767 0,4772 0,4783 0,4793 0,4803 0,4812 0,4821 0,4830 0,4838 0,4846 0,4854 0,4861 0,4868 0,4875 0,4881	2,28 2,30 2,32 2,34 2,36 2,38 2,40 2,42 2,44 2,46 2,48 2,50 2,52 2,54 2,56 2,58 2,60 2,62 2,64 2,66 2,68 2,70 2,72 2,74 2,76 2,78 2,80 2,82 2,84 2,86 2,88 2,90 2,92 2,94 2,96 2,98 3,00 3,20 3,40 3,60 3,80 4,00 4,50 5,00	0,4887 0,4893 0,4898 0,4904 0,4909 0,4913 0,4918 0,4922 0,4927 0,4931 0,4934 0,4938 0,4941 0,4945 0,4948 0,4951 0,4953 0,4956 0,4959 0,4961 0,4963 0,4965 0,4967 0,4969 0,4971 0,4973 0,4974 0,4976 0,4977 0,4979 0,4980 0,4981 0,4982 0,4984 0,4985 0,4986 0,49865 0,49931 0,49966 0,499841 0,499928 0,499968 0,499997 0,499997

определим для Р/2 = = 0,475 аргумент функции Лапласа = 1,96.

Следовательно, доверительный интервал результата измерений, в мм:

(19,95 - 0,02 1,96) < х < (19,95 + 0,02 1,96)

или 19,91 < х < 19,99.

При нахождении случайной погрешности с использованием функции Лапласа доверительная вероятность по формуле

характеризует вероятность того, что отдельные единичные измерения хi не будут отклоняться от истинного значения более чем при большом числе измерений.

Однако при определении доверительного интервала при многократных измерениях важнее знать отклонение от истинного значения среднего арифметического значения ряда измерений. Из математической статистики известно, что если результат единичных измерений при небольшом числе измерений подчиняется нормальному закону, то распределение средних арифметических значений ряда измерений подчиняется закону Стьюдента с тем же средним арифметическим значением . Особенностью распределения Стьюдента является то, что доверительный интервал с уменьшением числа измерений расширяется по сравнению с нормальным законом распределения при той же доверительной вероятности. В связи с этим при ограниченном числе измерений, определяя доверительный интервал, рекомендуется использовать распределение Стьюдента.

Пример. При многократном измерении диаметра вала 30 h9(-0,0052) микрометром МК25-1 получены следующие результаты:

Измерение микрометром размера вала мм
№	1	2	3	4	5	6	7
И	29,94	29,95	29,96	29,97	29,97	29,98	29,98

Не учтенная систематическая погрешность, вызванная отклонением температуры вала от нормальной, = 2 мкм.

Определить, является ли результат х1 = 29,94 мм промахом, найти и записать в стандартной форме результат измерений (доверительная вероятность P=0,95).

1. Определим среднее арифметическое значение измеряемой величины, мм:

2. Рассчитаем СКП единичных измерений, мм:

3. Так как число измерений n < 10, а закон распределения результатов единичных измерений неизвестен, промах вычислим с использованием критерия Романовского:

Для ближайшего меньшего n = 6 и q = 0,05 (при Р = 0,95) по таблице Романовского найдем = 2,10, т.е. < и результат х1 = 29,94 промахом не является.

Значения

Уровень значимости q	Число измерений
	n=4	n=6	n=8	n=10	n=12	n=14	n=16
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,69	2,78
0,10	1,69	2,00	2,17	2,29	2,39	2,49	2,62

4. Определим СКП результата измерений среднего арифметического значения, мм:

5. Для заданной вероятности Р = 0,95 и числа измерений n = 7 по таблице коэффициентов. Стьюдента ( при К=6 ) установим значение коэффициента Стьюдента tp = 2,45.

Коэффициенты Стьюдента tp

К = n - 1	Заданная вероятности Р
	0,90	0,95	0,98	0,99	0,999
1	6,31	12,70	31,80	63,70	66,60
2	2,92	4,30	6,96	9,92	31,60
3	2,35	3,18	4,54	5,84	12,90
4	2,13	2,78	3,75	4,60	8,61
5	2,02	2,57	3,36	4,03	6,87
6	1,94	2,45	3,14	3,71	5,96
7	1,89	2,36	3,00	3,50	5,41
8	1,86	2,31	2,90	3,36	5,04
9	1,83	2,26	2,82	3,25	4,78
10	1,81	2,23	2,76	3,17	4,59
15	1,75	2,13	2,60	2,95	4,07
20	1,72	2,09	2,53	2,85	3,85
30	1,70	2,04	2,46	2,75	3,65
50	1,68	2,01	2,40	2,68	3,50
100	1,66	1,98	2,36	2,63	3,39
500	1,65	1,96	2,33	2,59	3,31

Тогда доверительные границы случайной погрешности результата измерений, мм:

6. Результат измерений запишем в виде А = 29,964 ± 0,014, P=0,95.

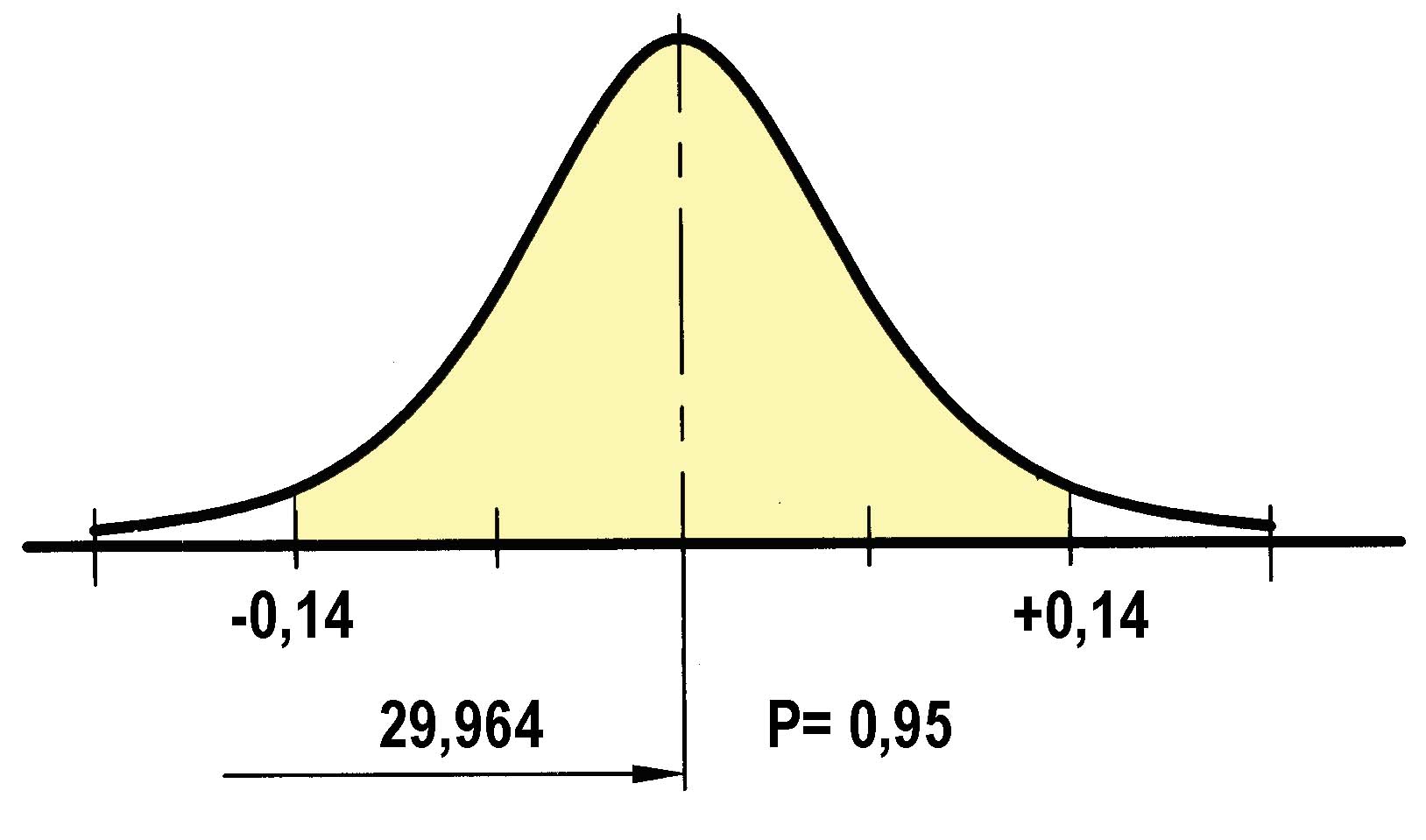
Однократные измерения

Большинство технических измерений являются однократными. В производственных условиях их точность может быть вполне приемлемой. При однократных измерениях процедура измерений регламентируется заранее, с тем чтобы при известной точности средств измерений и условиях измерения погрешность не превзошла определенное значение, т.е. значения D и Р заданы исходно. Так как такие измерения выполняют без повторений, то нельзя отделить случайные погрешности, от систематических. Для оценки погрешности дают лишь ее границы с учетом возможных влияющих величин.

Однократные измерения возможны при следующих условиях:

- объем априорной информации об объекте измерений такой, что однократные измерения не вызывают сомнений;

-изучен метод измерения, его погрешности либо заранее устранены, либо оценены;

- метрологические характеристики средств измерений соответствуют установленным нормам.

При однократных измерениях возможно образование инструментальной, методической и субъективной погрешностей. Если последние погрешности две не превышают 15% погрешности средства измерений, тогда погрешность измерения принимают равной погрешности используемого средства измерений

Однократный отсчет показаний может тоже содержать промах. Во избежание промаха при выполнении однократных измерений рекомендуется повторять измерения 2-3 раза, приняв за результат среднее арифметическое.

В простейшем случае, если влияющие величины соответствуют нормальной области значений, погрешность результата прямого однократного измерения равна основной погрешности средства измерений Dси , определяемой по нормативно-технической документации. Тогда результат измерения записывают в виде

А = Хси ± Dси , Р,

где Хси - результат (среднее арифметическое значение из 2-3 единичных измерений), зафиксированный средством измерений.

Доверительная вероятность Р, как правило, составляет 0,95. При проведении измерений в условиях, отличных от нормальных, необходимо определять и учитывать пределы дополнительных погрешностей, вызванных имеющимися отличиями.

Пример. Произведены измерения длины L = 50 ± 0,3 мм стержня штангенциркулем ШЦ-П, основная погрешность которого составляет Dси = ± 0,05 мм. Получены следующие результаты:Х1 = 50,10 мм; Х2 = 50,20 мм; Х3 = 50,15 мм. Записать окончательный результат измерений в стандартной форме:

Среднее арифметическое измеряемого размера.

Результат измерения запишем в виде

А = 50,15 ± 0,05 ; 0,95.

При неизвестной же погрешности средства измерения оценка производится на основе СКО

Пример... При измерении размера вала 55u8() получены следующие результаты, мм:

х1=55,01; х2=55,13; х3=55,12; х4=55,12; х5=55,12.

Провести точную оценку результатов измерений:

мм;

мм;

Таким образом, результат измерений

.

Если же, ввести доверительную вероятность Р= 0,95 то можно определить и доверительный интервал.

Статистические

VQ<<VQX

Совокупные

L1, L2, L3…

Совместные

L, M, T…

Измерения

Однократные

n=1

Динамические

VQVQX

Косвенные

Q=F(X, Y…)

Метрологические

0

Технические

[]

Ориентировочные

[]=

По сопоставлению серий 1 и 2

Равноточные

1=2

Неравноточные

12

Прямые

Q=X

бсолютные

Q=X

Относительные

Q=X/Xнорм

Многократные

n1

Погрешность измерения