Способи перетворення комплексного креслення
Кафедра "Прикладна геометрія інформаційні технології проектування" ТДАТУ
Викладач: доц. Щербина В.М.
Конспект лекцiї № 4
з дисципліни "Нарисна геометрія, інженерна та комп'ютерна графіка"
Тема лекцiї: Способи перетворення комплексного креслення
Мета та задачі: Показати, на скільки спрощується розв’язання метричних, позиційних задач з використанням методів перетворення епюру. Розглянути суть способу обертання навколо проекціюючої прямої, а також способу заміни площин проекцій.
Знання та вмiння, якi студенти повиннi отримати:
Студенти повинні:
Знати: схему побудови нової проекції точки.
Вміти: перетворювати геометричні об’єкти із загального положення в приватне.
План
4.1. Суть способів перетворення комплексного креслення.
4.2. Обертання навколо проекцюючої прямої.
4.3. Перетворення креслення за способом заміни площин проекцій.
4.4. Основні задачі способу заміни площин проекцій.
4.5. Метричні задачі.
Література
- С.30–37.
- С. 110-112.
- С. 81-90.
- С. 17-19.
- С.109–154.
- Діафільми "Проецирование точки", "Вращение".
- Плакати Л 6-1 ... Л 6-4.
- Макети НГ- 1, НГ- 28.
4.1. Суть способів перетворення комплексного креслення.
Для розв'язання метричних та позиційних задач використовують способи перетворення креслення (обертання та зміна площин проекцій),які полягають у зміні взаємо розташування геометричного образу та площин проекцій.
В результаті обертання геометричний образ займає окреме положення відносно нерухомих площин проекцій.
У другому випадку площини проекцій замінюють новими, які займають окреме положення відносно нерухомого геометричного образу.
4.2. Обертання навколо проекцюючої прямої.
Під час обертання усі точки фігури, що обертається, описують у просторі дуги кіл, площини яких є перпендикулярними до осі обертання. Центри цих дуг розташовуються на осі обертання, а радіуси являють собою найкоротшу відстань від точок, що обертаються навколо осі.
Для спрощення побудови осі обертання розташовують перпендикулярно до однієї з площин проекцій.
Під час обертання точки навколо горизонтально – проекцюючої осі горизонтальна проекція точки переміщується за колом з центром у горизонтальній проекції осі обертання, а фронтальна – за прямою, паралельною до осі Ох (рис.4.1).
Алгоритм способу обертання навколо проекцюючої прямої.
1. Через точку А проводимо площину переміщення Р (Р// П1) - Рi.
2. Знаходимо центр обертання Рi=0.
3. Визначаємо радіус обертання ОА = R.
4. Знаходимо натуральну величину радіуса обертання А1О1 = R об.н.в.
5. Будуємо нове положення точки А (), яке вона займатиме опісля повороту на кут .
Навпаки, якщо вісь обертання розташована перпендикулярно до площини П2, то горизонтальні проекції точок будуть переміщуватися за прямою, паралельною осі Ох, а фронтальна - за колом (рис.4.2).
Обертання будь–якої фігури навкруг проекцюючої прямої зводиться до обертання точок цієї фігури (рис.4.3).
Рис.4.3.
Визначення натуральної величини відрізку АВ способом
обертання навколо осі і, яка є перпендикулярною до П1
Точка А, розташована на осі i, після повороту не змінює свого розташування.
Для побудови точки В дотримуємося алгоритму обертання навколо проекцюючої прямої (див. вище).
4.3. Перетворення креслення за способом заміни площин проекцій.
Під час розв'язання практичних задач за способом заміни площин проекцій необхідно враховувати, як правило, дві обставини:
–нова площина проекцій має бути перпендикулярною до однієї із завданих площин проекцій, забезпечуючи таким чином ортогональність нової системи площин проекцій;
–нова площина проекцій має займати окреме положення відносно геометричного образу, забезпечуючи при цьому спрощення розв'язання задачі.
Площина П4 перетинається з площиною П1 за прямою Х14, яка позначує нову вісь проекцій. Розташування горизонтальної проекції А1 точки А залишається без зміни, тому що т. А та площина П1 не змінюють свого розташування у просторі. Для знаходження нової фронтальної проекції точки А4, достатньо спроектувати ортогонально т. А на площину П4.
Нова проекція точки будується за наступною схемою:
1. З незмінної проекцiї точки (А2) проводять лінію зв'язку перпендикулярно до нової осі Х14.
2. Від нової осі (X14) до нової проекції (А4) відкладають відстань, що дорівнює відстані від змінної проекцiї точки (А2) до змiнної осі (х).
.
4.4. Основні задачі способу заміни площин проекцій.
4.4.1. Пряму загального положення перетворити в пряму рівня (рис.4.5.). Нову вісь проводять паралельно до однiєї з проекцій прямої.
4.4.2. Пряму рівня перетворити у проекцюючу пряму (рис.4.6).
Нова площина проекцій обирається перпендикулярно до прямої рівня.
4.4.3. Площину загального положення перетворити у проекцюючу площину. Нова площина проекцій обирається перпенди-кулярно до лінії рівня (до горизонталі) на рис.4.7 та вирішується задача 4.4.2.
4.4.4. Проекцюючу площину перетворити в площину рівня (рис.4.8). Нова площина проекцій проводиться паралельно до завданої площини .
4.5. Метричні задачі.
Метрична задача - це задача, що зв'язана з визначенням натуральної величини відрізків або кутів.
Наприклад:
1. Визначення натуральної величини відрізка розв'язанням задачі 4.4.1. (рис.4.6) за способом заміни площин проекцій або обертанням навколо проекцюючої осі (рис.4.3).
2. Визначення натуральної величини плоскої фігури розв'язанням задачі 4.4.3 та 4.4.4 за способом заміни площин проекцій (рис.4.7, 4.8).
Перелік метричних задач, які вирішуються з використанням способів перетворювання комплексного креслення.
Відстань між: двома точками,
точкою та прямою,
паралельними прямими,
точкою та площиною,
паралельними площинами,
прямими, що перехрещуються.
Кут між : двома прямими, що перетинаються (перехрещуються),
прямою та площиною,
двома площинами.
EMBED Equation.3 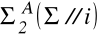
EMBED Equation.3 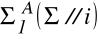
EMBED Equation.3 
EMBED Equation.3 
EMBED Equation.3 
EMBED Equation.3 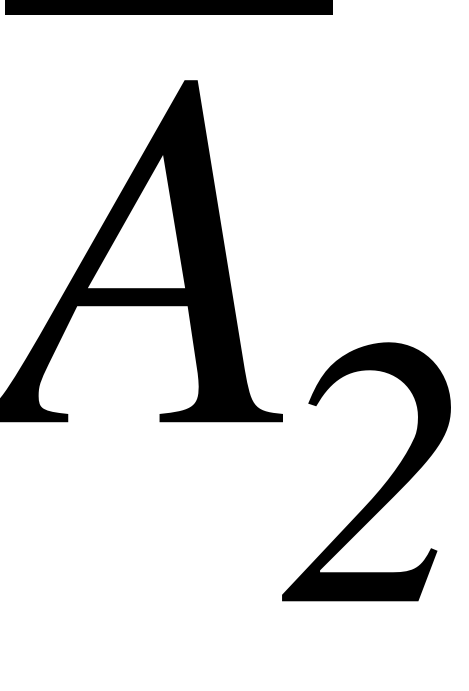
EMBED Equation.3 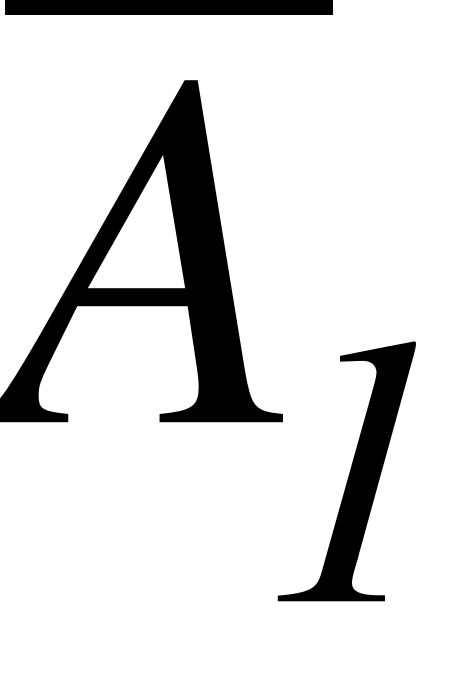
EMBED Equation.3 
EMBED Equation.3 
Рис.4.1.
Обертання точки А
навколо осі іEMBED Equation.3 П1
П1
Рис.4.2.
Обертання точки А
навколо осі іEMBED Equation.3 П2
П2
EMBED Equation.3 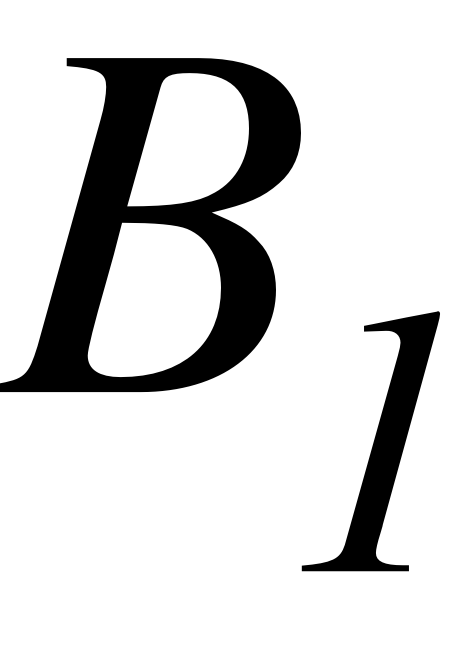
EMBED Equation.3 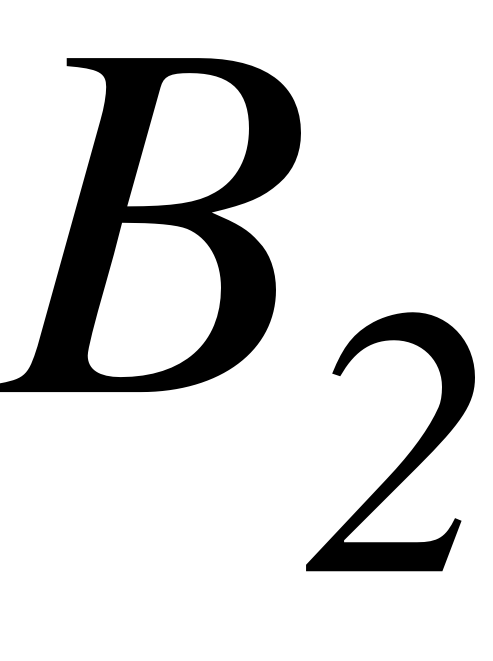
EMBED Equation.3 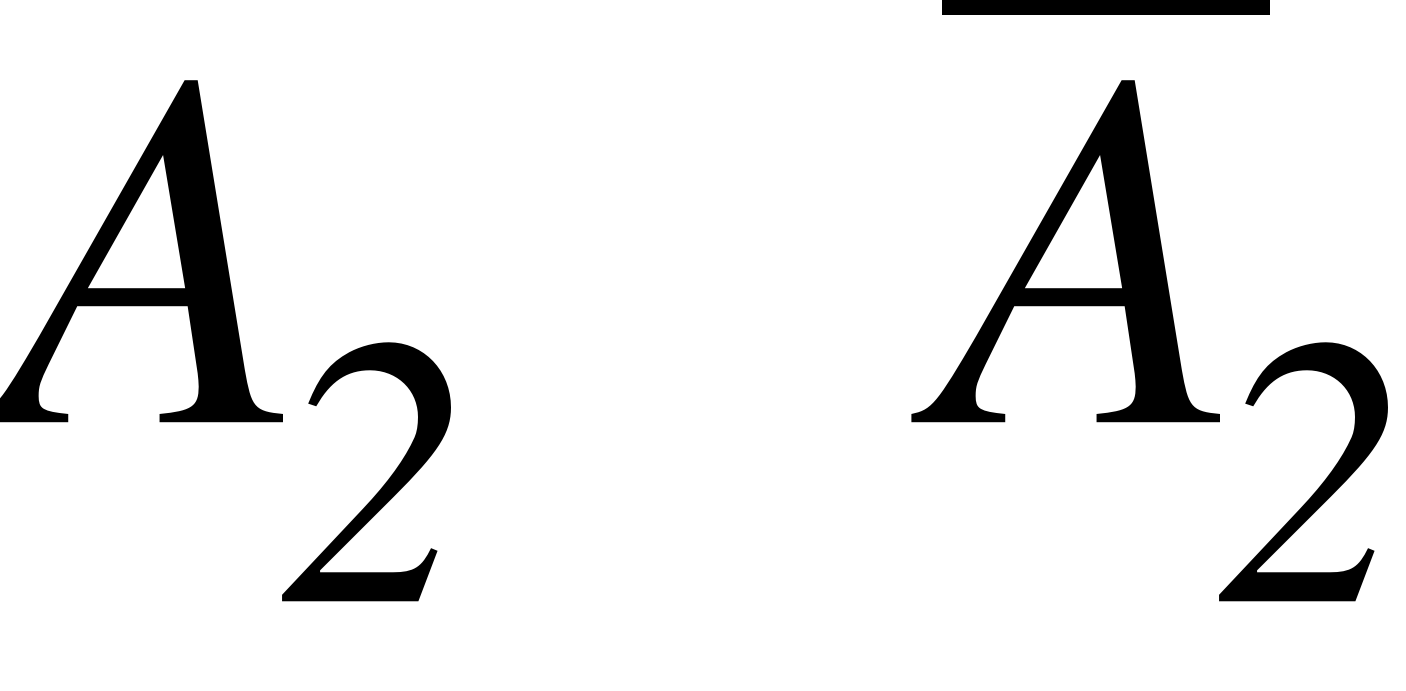
EMBED Equation.3 
EMBED Equation.3 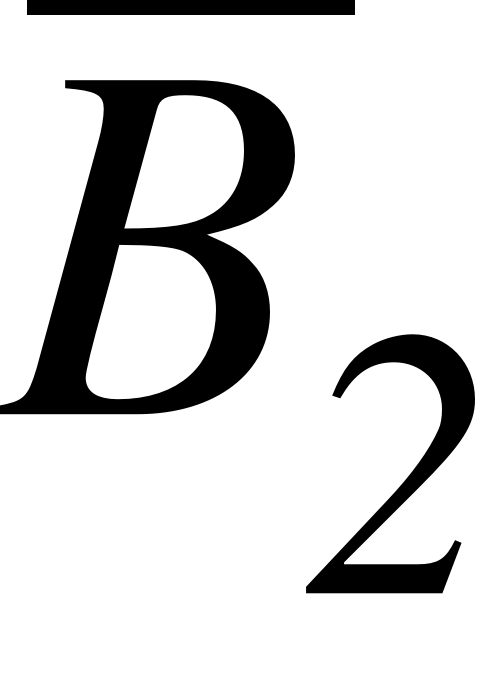
EMBED Equation.3 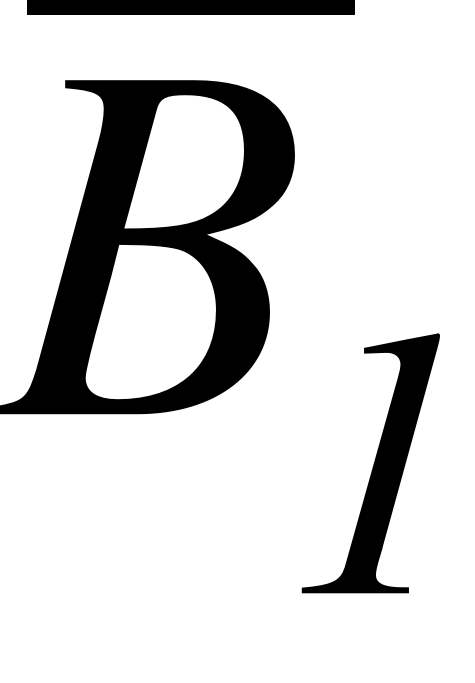
EMBED Equation.3 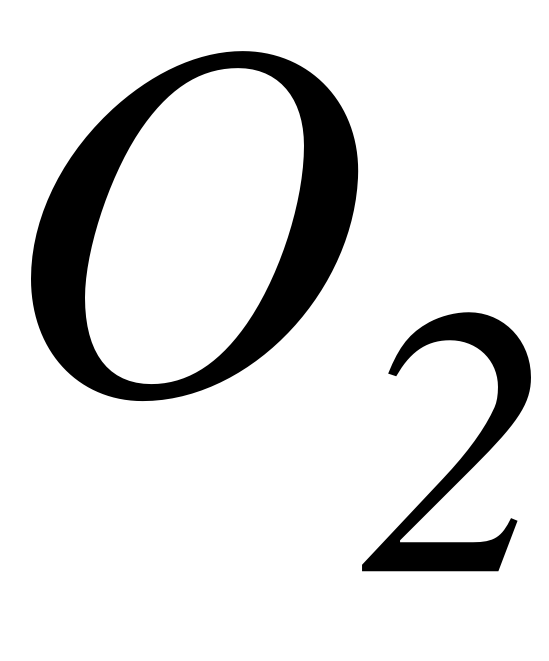
EMBED Equation.3 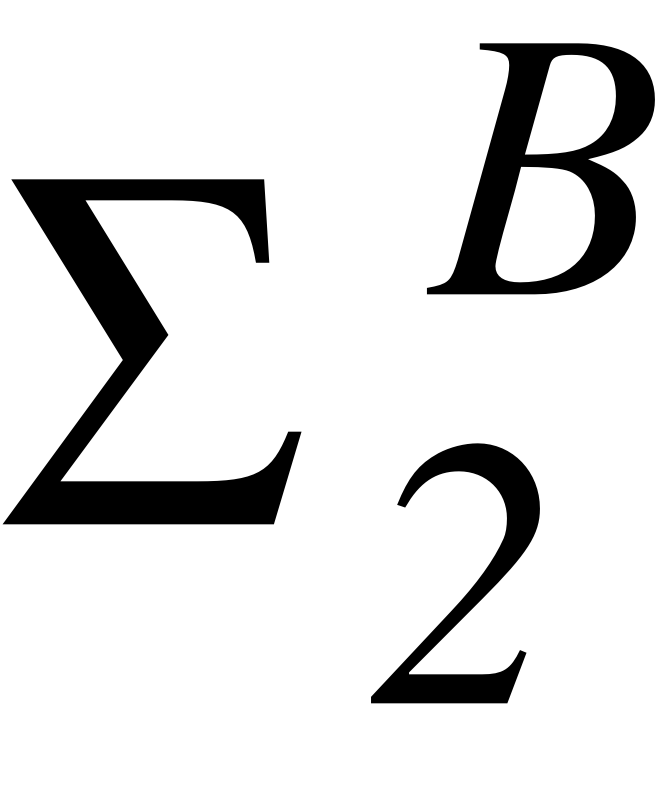
Н.В.
П1
А12
А14
А
А2
А1
А4
П1
x14
x12
П4
П2
x14
x14
П2
П4
x12
А4
А1
А2
П4
А14
А12
П1
x12
А4
А1
А2
В4
В1
П1
П1
П2
В2
Рис.4.5.
Рис.4.6.
В2
x14
П4
x12
А4В4
А1
А2
Рис.4.7.
В1
П1
П1
П2
Рис.4.8.
h2
x14
П4
x12
14
11
12
h1
П1
П1
П2
Р1
Р2
Рх
Рx1
Р4
Рис.4.4.
Схема отримання "нової" проекції точки в новій системі
В2
x14
П4
x12
А4
А1
А2
В1
П1
П1
П2
В4
C4
C1
C2
Способи перетворення комплексного креслення