Введение в теорию множеств

аранов Виктор Павлович. Дискретная математика. Раздел 1. Элементы теории множеств.

Лекция 1. Введение в теорию множеств

Лекция 1. ВВЕДЕНИЕ В ТЕОРИЮ МНОЖЕСТВ

План лекции:

Обзор содержания курса.
Основные понятия теории множеств.
Способы задания множеств.
Операции над множествами.
Теоретико-множественные тождества.
Прямое произведение множеств.

Обзор содержания курса

Дискретная математика – часть математики, которая зародилась в глубокой древности. Как следует из названия курса, главной его спецификой является дискретность, которая является антиподом непрерывности. Дискретность и непрерывность вместе составляют единство, которое характерно для математики. В качестве примера можно привести числовые системы: множество натуральных чисел – дискретный объект, а множество действительных чисел – непрерывный. Другой пример: при численном решении какой-либо задачи, связанной с исследованием и расчетом непрерывного объекта (расчет траектории движения материального тела, определение формы поверхности, преобразование непрерывного сигнала, анализ временных рядов и др.) главным этапом является дискретизация задачи, т. е. выбор адекватной дискретной модели, результаты расчета которой с заданной степенью точности позволяют найти искомые величины в непрерывной задаче.

Классическая математика – это математика непрерывных величин. Основное понятие классической математики, понятие предела, связано с представлением о непрерывной действительной прямой – континууме. Основная модель классической математики – система дифференциальных уравнений, описывающая движение по непрерывной траектории в фазовом пространстве.

Элементы дискретной математики зародились в рамках классической, но до середины XX века не занимали в ней заметного места.

В широком смысле дискретная математика включает в себя и такие сложившиеся разделы математики, как теория чисел, алгебра, математическая логика и ряд разделов, которые наиболее интенсивно стали развиваться в середине XX века в связи с научно-техническим прогрессом, прежде всего связанным с широким использованием компьютеров. Последнее привело к необходимости изучения сложных управляющих систем. В узком смысле слова дискретная математика ограничивается только этими новыми разделами. Именно в узком смысле понимается дискретная математика при изучении данного курса. К упомянутым новым разделам, составляющим содержание курса, относятся: комбинаторный анализ, теория графов и сетей, теория функциональных систем (теория булевых функций), теория конечных автоматов и формальных языков, теория алгоритмов. Кроме того, можно добавить следующие разделы, которые в данном курсе не рассматриваются: теория кодирования, целочисленное программирование и др.

В настоящее время дискретная математика является не только фундаментом математической кибернетики, но и важным звеном математического образования. Главная задача данного курса – это обучение методам и мышлению, характерным для дискретной математики.

Основные понятия теории множеств

Понятие множества является первичным и поэтому формально не может быть определено. Обычно множество объясняют, следуя основателю теории множеств Г. Кантору, как совокупность объектов произвольной природы, рассматриваемую, как единое целое.

Объекты, составляющие множество, называют его элементами. Множества обозначают прописными буквами латинского алфавита (), элементы множеств – строчными буквами ().Утверждение «элемент принадлежит множеству » записывается следующим образом: ( – символ принадлежности). В противном случае – (или ).

Если каждый элемент множества входит в множество , то называется подмножеством . При этом пишут: или . Если и , то пишут или . Здесь ,, , – символы включения. Множества и равны, если они состоят из одних и тех же элементов, иначе говоря, если и .

Множество, не содержащее ни одного элемента, называется пустым (обозначается ). Множество называется истинным, если оно не пустое.

Из определения подмножества следует, что каждое множество является подмножеством самого себя: . Кроме того, считают, что пустое множество есть подмножество любого множества : .

Различают два вида подмножеств множества : само и называют несобственными подмножествами; все остальные подмножества, если они существуют, – собственными.

В теории множеств для удобства и краткости записей используют специальные обозначения:

– квантор общности (означающий «любой», «для всех», «каков бы ни был»);

– квантор существования (означающий «существует», «найдется», «можно найти»);

– импликация (символ следствия, означающий «влечет за собой).

С помощью этих символов условие запишется так:

Множество называется эквивалентным множеству (обозначается ), если между элементами и можно установить взаимно однозначное соответствие. Различают конечные и бесконечные множества. Число элементов множества называется его мощностью или кардинальным числом и обозначается или card (англ. cardinality – мощность). Таким образом, конечное множество, содержащее элементов, имеет мощность . Если эквивалентно множеству натуральных чисел , то его называют счетным и его мощность обозначается через . Множество , эквивалентное множеству действительных чисел , называется континуальным, а его кардинальное число c – мощностью континуума.

Способы задания множеств

Для задания множества существуют различные способы. Множество считают заданным, если о каждом элементе можно сказать, принадлежит он данному множеству или нет.

Задание множества с использованием общепринятых обозначений. Для числовых множеств имеем: – множество натуральных чисел; – множество целых чисел; – множество рациональных чисел; – множество действительных чисел; – множество комплексных чисел.

Задание множества перечислением его элементов. Конечное множество можно задать перечислением его элементов и записать в виде

Например, {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – множество десятичных цифр.

Задание множества с помощью характеристического свойства его элементов. Характеристическое свойство – это свойство, которым обладают все элементы данного множества и только они. Этот способ применим для конечных и бесконечных множеств.

Пусть – утверждение, заключающееся в том, что элемент обладает свойством . Тогда запись

означает, что рассматривается множество всех элементов , обладающих свойством .

Например, отрезок [0, 1] действительной прямой можно определить следующим образом

Рекурсивное задание множества. Этот способ заключается в следующем:

1. Указываются некоторые исходные элементы, входящие в множество.

2. Описывается механизм, позволяющий получить новые элементы из имеющихся.

3. Объявляется, что в множестве нет никаких других объектов кроме тех, которые можно получить из исходных, применяя описанный в п. 2 механизм.

Например, множество можно задать рекурсивно:

1. .

2. .

3. – наименьшее подмножество натурального ряда, удовлетворяющее условиям 1 и 2.

Условие 3 определяет как пересечение всех множеств, удовлетворяющих условиям 1 и 2.

В дальнейшем при рекурсивном задании множеств последний пункт, как правило, не указывается, но всякий раз это требование подразумевается.

В качестве еще одного примера рекурсивного задания множества определим совокупность всех слов в данном алфавите.

Пусть – произвольное конечное множество, элементы которого будем называть буквами, а само множество алфавитом. Элементы определяемого множества будем называть словами.

1. Каждая буква является словом: , 1, 2, …, .

2. Результат приписывания к слову любой буквы является словом:

…, .

Например, если , то содержит следующие элементы:

0, 1 (согласно 1);

00, 01, 10, 11 (согласно 2);

000, 001, 010, 011, 100, 101, 110, 111 (согласно 2) и так далее.

Теория множеств, рассматриваемая без ограничений на способы задания множеств, называется наивной теорией множеств. В этой теории еще при жизни ее создателя Г. Кантора были обнаружены многочисленные парадоксы. Приведем один из известных парадоксов Б. Рассела, открытый им в 1903 г.

Пусть – множество всех множеств, которые не содержат себя в качестве своего элемента. Содержит ли множество само себя в качестве элемента? Если да, то, по определению , оно не должно быть элементом – противоречие. Если нет – то, по определению , оно должно быть элементом – вновь противоречие.

Этот парадокс имеет много популярных формулировок. Приведем некоторые из них.

Одному полковому брадобрею приказали «брить всякого, кто сам не бреется, и не брить того, кто сам бреется». Как он должен поступить с собой?
В одной стране вышел указ: «Мэры всех городов должны жить не в своем городе, а в специальном Городе мэров». Где должен жить мэр Города мэров?
Некая библиотека решила составить библиографический каталог, в который входили бы все те и только те библиографические каталоги, которые не содержат ссылок на самих себя. Должен ли такой каталог включать ссылку на себя?

Для преодоления противоречий в наивной теории множеств было предложено несколько возможных ее аксиоматизаций, в рамках которых утверждение о существовании множества всех множеств было бы невыводимым.

Операции над множествами

Во многих случаях удается избежать противоречий наивной теории множеств, если выбрать некоторое так называемое универсальное множество и ограничиться рассмотрением только его подмножеств.

Если некоторые множества взять в качестве исходных, то из них можно получить новые с помощью следующих операций.

Объединением множеств и (обозначение ) называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств или :

Вместо символа объединения используется также символ +.

Пересечением множеств и (обозначение ) называется множество, состоящее из элементов, принадлежащих каждому из множеств и :

Для операции пересечения используются также другие обозначения:

Аналогично определяются объединение и пересечение произвольной совокупности множеств , . Здесь – множество индексов. Если – множество первых натуральных чисел, то употребляются обозначения и , а в случае если , то будем писать и .

Разностью множеств и (обозначение ) называется множество, состоящее из всех элементов , не принадлежащих:

В отличие от двух предыдущих операций разность некоммутативна: . Если , то .

Симметрической разностью множеств и (обозначение ) называется множество элементов и , которые содержатся только в одном из этих множеств:

Дополнением к множеству (обозначение ) относительно универсального множества называется множество:

или .

Операции объединения, пересечения и дополнения часто называют булевыми операциями над множествами. Так как операция разности не обладает свойством ассоциативности, то ее выражают через другие операции, например, операции дополнения и пересечения:

Универсальное множество позволяет геометрически изображать множества и операции над ними с помощью диаграмм Венна (рис. 1).

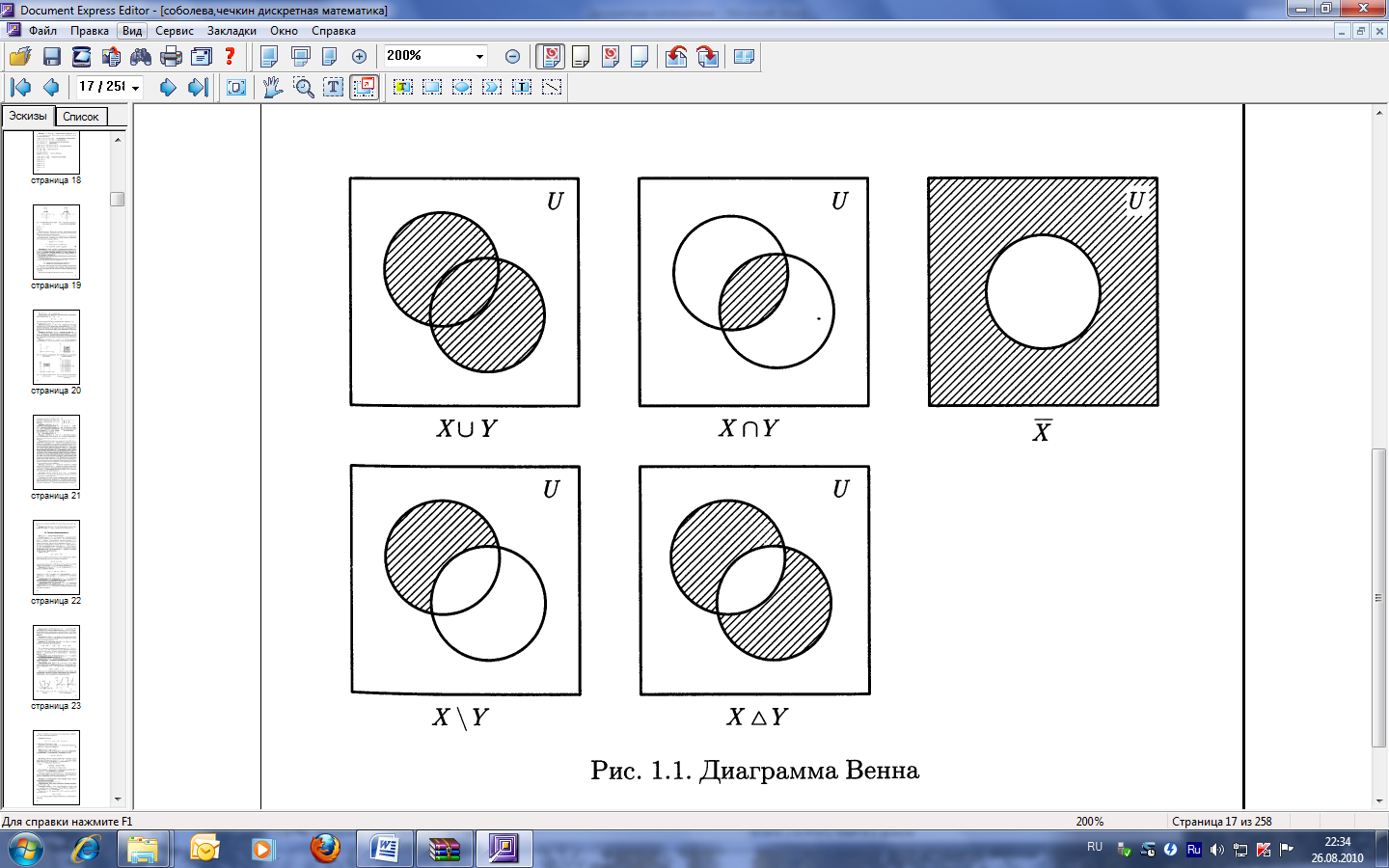
Рис. 1. Диаграммы Венна

Теоретико-множественные тождества

Пусть – универсальное множество, а – его подмножества. Тогда имеют место следующие тождественные равенства.

ассоциативность объединения и пересечения.

коммутативность объединения и пересечения.

дистрибутивность.

идемпотентность.

законы де Моргана.

дополнимость.

13. – закон двойного дополнения.

существование универсальных границ.

законы дополнения.

Приведенная система тождеств является полной в том смысле, что любое соотношение между множествами является следствием этих тождеств: Справедливость равенств 1 – 19 можно установить, используя принцип равнообъёмности, согласно которому нужно доказать, что множества, стоящие в левой и правой частях равенства состоят из одних и тех же элементов. В качестве примера приведем доказательство равенства 9. Остальные тождества доказываются аналогично. Имеем:

Прямое произведение множеств

Прямым произведением множеств и называют множество , элементами которого являются всевозможные упорядоченные пары , такие, что , :

Эта операция над множествами, в отличие от рассмотренных ранее, изменяет природу элементов: в новом множестве элементами являются пары.

Прямое произведение в общем случае не обладает свойствами коммутативности и ассоциативности: , .

Пусть теперь даны множеств: . Упорядоченный набор из элементов, таких, что , ,…, , называется вектором или кортежем. Множество таких векторов представляет собой прямое произведение множеств :

Если , то множество называется степенью (прямой) множества и обозначается через .

Проекцией вектора на -ю ось (обозначение ) называется его компонента. Проекцией вектора на оси с номерами называется вектор длины (обозначение ).

Пусть – множество векторов одинаковой длины. Тогда проекцией множества на -ю ось называется множество проекций всех векторов на -ю ось: . Аналогично определяется проекция множества на несколько осей: .

Пример 1. Пусть .Тогда прямым произведением является множество точек плоскости, то есть пар вида , где и являются координатами точек плоскости.

Координатное представление точек плоскости, предложенное французским математиком и философом Р. Декартом, является исторически первым примером прямого произведения. Потому прямое произведение называют также декартовым.

Пример 2. Пусть , . Тогда – множество, содержащее обозначения всех 64 клеток шахматной доски.

Введение в теорию множеств