ОПЫТНОЕ ОБОСНОВАНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ

Согласно молекулярно-кинетической теории все вещества состоят из мельчайших частиц - молекул. Молекулы находятся в непрерывном движении и взаимодействуют между собой. Молекула - наименьшая частица вещества, обладающая его химическими свойствами. Молекулы состоят из более простых частиц - атомов химически элементов. Молекулы различных веществ имеют различный атомный состав.

Молекулы обладают кинетической энергией Eкин и одновременно потенциальной энергией взаимодействия Eпот. В газообразном состоянии Eкин > Eпот. В жидком и твердом состояниях кинетическая энергия частиц сравнима с энергией их взаимодействия.

Три основных положения молекулярно - кинетической теории:

1. Все вещества состоят из молекул, т.е. имеют дискретное строение, молекулы разделены промежутками.

2. Молекулы находятся в непрерывном беспорядочном (хаотическом) движении.

3. Между молекулами тела существуют силы взаимодействия.

Молекулярно-кинетическая теория обосновывается

Приведем некоторые из доказательств беспорядочного (хаотического) движения молекул:

а) стремление газа занять весь предоставленный ему объем (распространение пахучего газа по всему помещению);

б) броуновское движение - беспорядочное движение мельчайших видимых в микроскоп частиц вещества, находящихся во взвешенном состоянии и нерастворимых в ней. Это движение происходит под действием беспорядочных ударов молекул, окружающей жидкости, находящихся в постоянном хаотическом движении;

в) диффузия - взаимное проникновение молекул соприкасающихся веществ. При диффузии молекулы одного тела, находясь в непрерывном движении, проникают в промежутки между молекулами другого соприкасающегося с ним тела и распространяются между ними. Диффузия проявляется во всех телах - в газах, жидкостях и твердых телах, - но в разной степени.

1. Диффузия.

Диффузию в газах можно наблюдать, если сосуд с пахучим газом открыть в помещении. Через некоторое время газ распространится по всему помещению.

Диффузия в жидкостях происходит значительно медленнее, чем в газах. Например, в стакан нальем раствор медного купороса, а затем, очень осторожно добавим слой воды и оставим стакан в помещении с постоянной температурой и где он не подвергается сотрясениям. Через некоторое время будем наблюдать исчезновение резкой границы между купоросом и водой, а через несколько дней жидкости перемешаются, несмотря на то, что плотность купороса больше плотности воды. Так же диффундирует вода со спиртом и прочие жидкости.

Диффузия в твердых телах происходит еще медленнее, чем в жидкостях (от нескольких часов до нескольких лет). Она может наблюдаться только в хорошо пришлифованных телах, когда расстояния между поверхностями пришлифованных тел близки к расстояниям между молекулами (10-8 см). При этом скорость диффузии увеличивается при повышении температуры и давления.

Доказательства силового взаимодействия молекул:

а) деформация тел под влиянием силового воздействия;

б) сохранение формы твердыми телами;

в) поверхностное натяжение жидкостей и, как следствие, явление смачивания и капиллярности.

Между молекулами существуют одновременно силы притяжения и силы отталкивания (рис. 1). При малых расстояниях между молекулами преобладают силы отталкивания. По мере увеличения расстояния r между молекулами, как силы притяжения, так и силы отталкивания убывают, причем силы отталкивания убывают быстрее. Поэтому при некотором значении r0 (расстояние между молекулами) силы притяжения и силы отталкивания взаимно уравновешиваются.

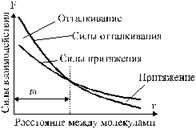
Рис. 1. Силы притяжения и силы отталкивания.

Если условиться отталкивающим силам приписывать положительный знак, а силам притяжения - отрицательный и произвести алгебраическое сложение сил отталкивания и притяжения, то получаем график, изображенный на рисунке 2.

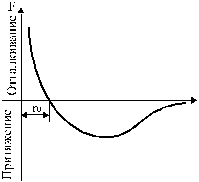
Рис. 2. Алгебраическое сложение сил отталкивания и притяжения.

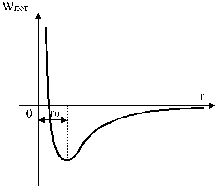
Рис. 3. Зависимость потенциальной энергии взаимодействия молекул от расстояния между ними.

На рисунке 3 дан график зависимости потенциальной энергии взаимодействия молекул от расстояния между ними. Расстояние r0 между молекулами соответствует минимуму их потенциальной энергии (рис. 3). Для изменения расстояния между молекулами в ту или другую сторону требуется затратить работу против преобладающих сил притяжения или отталкивания. На меньших расстояниях (рис. 2) кривая круто поднимается вверх; эта область соответствует сильному отталкиванию молекул (обусловленному главным образом кулоновским отталкиванием сближающихся ядер). На больших расстояниях молекулы притягиваются.

Расстояние r0 соответствует устойчивому равновесному взаимному положению молекул. Из рисунка 2 видно, что при увеличении расстояния между молекулами, преобладающие силы притяжения восстанавливают равновесное положение, а при уменьшении расстояние между ними равновесие восстанавливается преобладающими силами отталкивания.

Современные экспериментальные методы физики (рентгеноструктурный анализ, наблюдения с помощью электронного микроскопа и другие) позволили наблюдать микроструктуру веществ.

2. Число Авогадро.

Число граммов вещества, равное молекулярному весу этого вещества, называется грамм-молекулой или молем. Например, 2 г водорода составляет грамм-молекулу водорода; 32 г кислорода составляют грамм-молекулу кислорода. Масса одного моля вещества называется молярной массой этого вещества.

Обозначается через m. Для водорода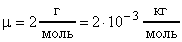; для кислорода 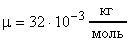; для азота 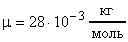и т.д.

Число молекул, содержащихся в одном моле разных веществ одинаково и называется числом Авогадро (NA).

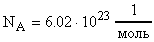
Число Авогадро чрезвычайно велико. Чтобы почувствовать его колоссальность, представьте себе, что в Черное море высыпали число булавочных головок (диаметр каждой около 1 мм), равное числу Авогадро. При этом оказалось бы, что в Черном море уже не остается места для воды: оно не только до краев, но и большим избытком оказалось бы заполненным этими булавочными головками. Авогадровым числом булавочных головок можно было бы засыпать площадь, равную, например, территории Франции, слоем толщиной около 1 км. И такое огромное число отдельных молекул содержится всего лишь в 18 г воды; в 2 г водорода и т.д.

Установлено, что в 1 см3 любого газа при нормальных условиях (т.е. при 00С и давлении 760 мм. рт. ст.) содержится 2,71019 молекул.

Если взять число кирпичей, равное этому числу, то, будучи плотно уложенными, эти кирпичи покрыли бы поверхность всей суши Земного шара слоем высотой 120 м. Кинетическая теория газов позволяет вычислить лишь длину свободного пробега молекулы газа (т.е. среднее расстояние, которое проходит молекула от столкновения до столкновения с другими молекулами) и диаметр молекулы.

Приводим некоторые результаты этих вычислений.

Вещество	Длина свободного пробега при 760 мм.рт.ст.	Диаметр молекулы
Водород Н2	1,12310-5 см	2,310-8 см
Кислород О2	0,64710-5 см	2,910-8 см
Азот N2	0,59910-5 см	3,110-8 см

Диаметры отдельных молекул - величины малые. При увеличении в миллион раз молекулы были бы величиной с точку типографского шрифта этой книжки. Обозначим через m - массу газа (любого вещества). Тогда отношение дает число молей газа.

Число молекул газа n можно выразить:

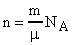(1).

Число молекул в единице объема n0 будет равно:

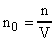(2) , где: V - объем газа.

Массу одной молекулы m0 можно определить по формуле:

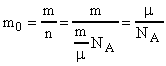(3) .

Относительной массой молекулы mотн называется величина, равная отношению абсолютной массы молекулы m0 к 1/12 массы атома углерода moc.

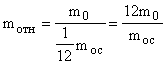(4), где moc = 210-26 кг.

3. Уравнение идеального газа и изопроцессы.

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трех параметров - давление, объем или температура - остаются неизменными. Количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра называют газовыми законами.

Процессы, протекающие при неизменном значении одного из параметров, называют изопроцессами (от греч. «изос» - равный). Правда, в действительности ни один процесс не может протекать при строго фиксированном значении какого-либо параметра. Всегда имеются те или иные воздействия, нарушающие постоянство температуры, давления или объема. Лишь в лабораторных условиях удается поддерживать постоянство того или иного параметра с хорошей точностью, но в действующих технических устройствах и в природе это практически неосуществимо.

Изопроцесс - это идеализированная модель реального процесса, которая только приближенно отражает действительность.

Процесс изменения состояния термодинамической системы макроскопических тел при постоянной температуре называют изотермическим.

Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой - термостатом. Иначе при сжатии или расширении температура газа будет меняться. Термостатом может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.

Согласно уравнению состояния идеального газа в любом состоянии с неизменной температурой произведение давления газа на его объём остаётся постоянным: pV=const при T=const. Для газа данной массы произведение давления газа на его объём постоянно, если температура газа не меняется.

Этот закон экспериментально был открыт английским учёным Р. Бойлером(1627 - 1691) и несколько позже французским учёным Э Мариоттом (1620 -1684). Поэтому он носит название закона Бойля - Мариотта.

Закон Бойля - Мариотта справедлив для любых газов, а так же и их смесей, например для воздуха. Лишь при давлениях, в несколько сотен раз больше атмосферного, отклонение от этого закона становится существенным.

Зависимость давления газа от объёма при постоянной температуре графически изображается кривой, которая называется изотермой. Изотерма газа изображает обратно пропорциональную зависимость между давлением и объёмом. Кривую такого рода в математике называют гиперболой.

Разным постоянным температурам соответствуют различные изотермы. При повышении температуры давление согласно уравнению состояния увеличивается, если V=const. Поэтому изотерма соответствующая более высокой температуре Т2, лежит выше изотермы, соответствующей более низкой температуре Т1.

Изотермическим процессом приближенно можно считать процесс медленного сжатия воздуха при расширении газа под поршнем насоса при откачке его из сосуда. Правда, температура газа при этом меняется, но в первом приближении этим изменением можно пренебречь

Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным (от греч. «барос» - вес, тяжесть).

Согласно уравнению [pic] в любом состоянии газа с неизменным давлением отношение объёма газа к его температуре остаётся постоянным: [pic] =const при p=const.

Для газа данной массы отношение объёма к температуре постоянно, если давление газа не меняется.

Этот закон был установлен экспериментально в 1802 году французским учёным Ж. Гей-Люссаком (1778 - 1850) и носит название закона Гей-Люссака.

Согласно уравнению объём газа линейно зависит от температуры при постоянном давлении: V=const T.

Эта зависимость графически изображается прямой, которая называется изобарой. Различным давлениям соответствуют разные изобары. С ростом давления объём газа при постоянной температуре согласно закону Бойля-Мариотта уменьшается. Поэтому изобара, соответствующая более высокому давлению p2, лежит ниже изобары, соответствующей более низкому давлению p1.

В области низких температур все изобары идеального газа сходятся в точке T=0. Но это не означает, что объём реального газа действительно обращается в нуль. Все газы при сильном охлаждении превращаются в жидкость, а к жидкостям уравнения состояния неприменимо.

Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня.

Процесс изменения состояния термодинамической системы при постоянном объёме называют изохорным (от греч. «хорема» - вместимость).

Из уравнения состояния [pic]вытекает, что в любом состоянии газа с неизменным объёмом отношение давления газа к его температуре остаётся неизменным: [pic] =const при V=const.

Для газа данной массы отношение давления к температуре постоянно, если объём не меняется.

Этот газовый закон был установлен в 1787 году французским физиком Ж.Шарлем (1746 - 1823) и носит название закона Шарля. Согласно уравнению:

[pic] =const при V=const давления газа линейно зависит от температуры при постоянном объёме: p=const T.

Эта зависимость изображается прямой, называемой изохорой.

Разным объёмам соответствуют разные изохоры. С ростом объёма газа при постоянной температуре давление его согласно закону Бойля-Мариотта падает. Поэтому изохора, соответствующая большему объёму V2, лежит ниже изохоры, соответствующей меньшему объёму V1.

В соответствии с уравнением все изохоры начинаются в точке T=0.

Значит, давление идеального газа при абсолютном нуле равно нулю.

Увеличение давления газа в любой ёмкости или в электрической лампочке при нагревании является изохорным процессом. Изохорный процесс используется в газовых термостатах постоянного объёма.

4. Температура.

Любое макроскопическое тело или группа макроскопических тел называется термодинамической системой.

Тепловое или термодинамическое равновесие - такое состояние термодинамической системы, при котором все ее макроскопические параметры остаются неизменными: не меняются объем, давление, не происходит теплообмен, отсутствуют переходы из одного агрегатного состояния в другое и т.д. При неизменных внешних условиях любая термодинамическая система самопроизвольно переходит в состояние теплового равновесия.

Температура - физическая величина, характеризующая состояние теплового равновесия системы тел: все тела системы, находящиеся друг с другом в тепловом равновесии, имеют одну и ту же температуру.

Абсолютный нуль температуры - предельная температура, при которой давление идеального газа при постоянном объеме должно быть равно нулю или должен быть равен нулю объем идеального газа при постоянном давлении.

Термометр - прибор для измерения температуры. Обычно термометры градуируют по шкале Цельсия: температуре кристаллизации воды (таяния льда) соответствует 0°С, температуре ее кипения - 100°С.

Кельвин ввел абсолютную шкалу температур, согласно которой нулевая температура соответствует абсолютному нулю, единица измерения температуры по шкале Кельвина равна градусу Цельсия: [Т] = 1 К (Кельвин).

Связь температуры в энергетических единицах и температуры в градусах Кельвина:

где k = 1,38*10 -23 Дж/К - постоянная Больцмана.

Связь абсолютной шкалы и шкалы Цельсия:

T = t + 273, где t - температура в градусах Цельсия.

Средняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре:

Учитывая равенство (1), основное уравнение молекулярно-кинетической теории можно записать так: p=nkT.

Основные уравнения молекулярно-кинетической теории идеального газа для давления.

Газ называют идеальным, если:

1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;

2) между молекулами газа отсутствуют силы взаимодействия;

3) столкновения молекул газа со стенками сосуда абсолютно упругие.

Реальные газы (например, кислород и гелий) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки к идеальным газам. Частицы идеального газа в промежутках между столкновениями движутся равномерно и прямолинейно. Давление газа на стенки сосуда можно рассматривать как ряд быстро следующих ударов газовых молекул о стенку. Рассмотрим, как вычислить давление, вызванное отдельными ударами. Представим себе, что по некоторой поверхности происходит ряд отдельных и частых ударов. Найдем такую среднюю постоянную силу <F>, которая, действуя в течение времени t, за которое происходили отдельные удары, произведет такое же действие, как и все эти удары в своей совокупности. В таком случае импульс этой средней силы за время t должен равняться сумме импульсов всех тех ударов, которые получила поверхность за это время, т.е.

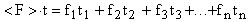, где t1, t2, t3 ... tn - время взаимодействия первой, второй, ..., n-й молекул со стенкой (т.е. длительность удара); f1, f2, f3 ... fn - силы удара молекул о стенку. Из этой формулы следует:

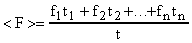(7).

Средняя сила давления, вызванная рядом отдельных ударов о некоторую поверхность, численно равна сумме импульсов всех ударов, полученных этой поверхностью за единицу времени называется изохорой.

5. Скорости газовых молекул.

Формулу (12) можно записать в виде:

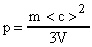(15), где 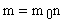(масса газа).

Из выражения (15) вычислим среднюю квадратичную скорость движения молекул газа:

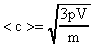
(16) .

Зная, что 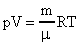(R-универсальная газовая постоянная; R=8,31 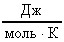), получим новые выражения для определения <c>.

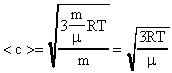(17) .

Опытное определение скоростей движения молекул паров серебра впервые был проведен в 1920 г Штерном.

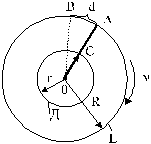
Рис. 5. Опыт Штерна.

Из стеклянного цилиндра Е выкачивался воздух (рис. 5). Внутри этого цилиндра помещался второй цилиндр Д, имеющий с ним общую ось О. Вдоль образующей цилиндра Д имелся прорез в виде узкой щели С. По оси протягивалась посеребренная платиновая проволока, по которой можно было пропускать ток. При этом проволока раскалялась, и серебро с ее поверхности обращалось в пар. Молекулы паров серебра разлетались в различные стороны, часть их проходила через щель С цилиндра Д и на внутренней поверхности цилиндра Е получался налет серебра в виде узкой полоски. На рис. 5 положение полоски серебра отмечено буквой А.

Когда вся система приводилась в очень быстрое движение таким образом, что проволока являлась осью вращения, то полоска А на цилиндре Е получилась смещенной в сторону, т.е. например, не в точке А, а в точке В. Это происходило потому, что пока молекулы серебра пролетали путь СА, точка А цилиндра Е успевала повернуться на расстояние АВ и молекулы серебра попадали не в точку А, а в точку В.

Обозначим величину смещения серебряной полоски АВ = d; радиус цилиндра Е через R, радиус цилиндра Д через r, а число оборотов всей системы в секунду через n.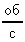

За один оборот системы точка А на поверхности цилиндра Е пройдет путь, равный длине окружности 2R, а за 1 секунду она пройдет путь 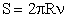. Время t, в течение которого точка А переместилась на расстояние АВ = d, будет равно: 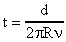. За время t молекулы паров серебра пролетали расстояние CA = R - r. Скорость их движения v может быть найдена, как пройденный путь, деленный на время: 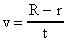или, заменяя t, получим: .

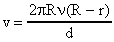Налет серебра на стенке цилиндра Д получался размытым, что подтверждало наличие различных скоростей движения молекул Из опыта можно было определить наиболее вероятную скорость vвер которая соответствовала наибольшей толщине налета серебра.

Наиболее вероятную скорость можно рассчитать по формуле, данной Максвеллом: 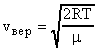(18). По вычислениям Максвелла средняя арифметическая скорость движения молекул равна: 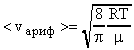(19).

6. Уравнение состояния идеального газа - уравнение Менделеева-Клапейрона.

Из основного уравнения молекулярно-кинетической теории (формула (14) следует закон Авогадро: в равных объемах разнородных газов при одинаковых условиях (одинаковой температуре и одинаковом давлении) содержится одинаковое число молекул: 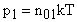(для одного газа), 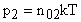(для другого газа).

Если V1 = V2; Т1 = Т2; r1 = r2, то n01 = n02.

Напомним, что единицей количества вещества в системе СИ является моль (грамм-молекула) масса m одного моля вещества называется молярной массой этого вещества. Число молекул, содержащихся в одном моле разных веществ одинаково и называется число Авогадро (NA = 6,021023 1/моль).

Запишем уравнение состояния идеального газа для одного моля: 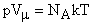, где Vm - объем одного моля газа; 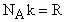, где Vm - объем одного моля газа; (универсальная газовая постоянная).

Окончательно имеем: 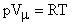(26).

Уравнение (26) называется уравнением Клапейрона (для одного моля газа). При нормальных условиях (р = 1,013105 Па и Т = 273,150К) молярный объем любого газа Vm = 22,410-3 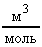. Из формулы (26) определим ; .

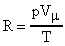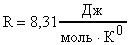От уравнения (26) для моля газа можно перейти к уравнению Менделеева-Клапейрона для любой массы газа m.

Отношение дает число молей газа. Левую и правую части неравенства (26) умножим на .

Имеем 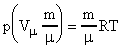, где 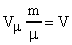объем газа.

Окончательно запишем: 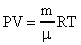(27). Уравнение (27) - уравнение Менделеева-Клапейрона. В это уравнение можно внести плотность газа 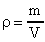и .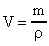

В формуле (27) заменим V и получим 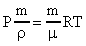или .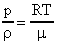

7. Опытные газовые законы. Давление смеси идеальных газов (закон Дальтона).

Опытным путем, задолго до появления молекулярно-кинетической теории, был открыт целый ряд законов, описывающих равновесные изопроцессы в идеальном газе. Изопроцесс - это равновесный процесс, при котором один из параметров состояния не изменяется (постоянен). Различают изотермический (T = const), изобарический (p = const), изохорический (V = const) изопроцессы. Изотермический процесс описывается законом Бойля-Мариотта: "если в ходе процесса масса и температура идеального газа не изменяются, то произведение давления газа на его объем есть величина постоянная PV = const (29). Графическое изображение уравнения состояния называют диаграммой состояния. В случае изопроцессов диаграммы состояния изображаются двумерными (плоскими) кривыми и называются соответственно изотермами, изобарами и изохорами.

Изотермы, соответствующие двум разным температурам, приведены на рис. 6.

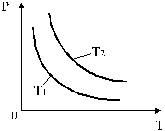
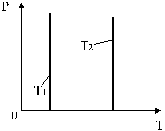
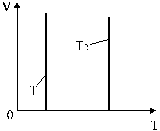
Рис. 6. Изотермы, соответствующие двум разным температурам.

Изобарический процесс описывается законом Гей-Люссака: "если в ходе процесса давление и масса идеального газа не изменяются, то отношение объема газа к его абсолютной температуре есть величина постоянная: 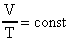(30).

Изобары, соответствующие двум разным давлениям, приведены на рис.7.

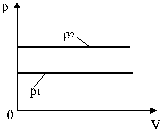
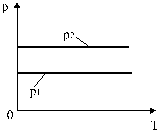
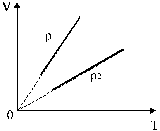
Рис. 7. Изобары, соответствующие двум разным давлениям.

Уравнение изобарического процесса можно записать иначе: 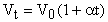31), где V0 - объем газа при 00С; Vt - объем газа при t0C; t - температура газа в градусах Цельсия; - коэффициент объемного расширения. Из формулы (31) следует, что 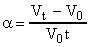. Опыты французского физика Гей-Люссака (1802 г.) показали, что коэффициенты объемного расширения всех видов газов одинаковы и 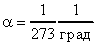, т.е. при нагревании на 10С газ увеличивает свой объем на часть того объема, который он занимал при 00С. На рис. 8 изображен график зависимости объема газа Vt от температуры t0C.

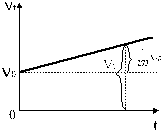
Рис. 8. График зависимости объема газа Vt от температуры t0C.

Изохорический процесс описывается законом Шарля: "если в ходе процесса объем, и масса идеального газа не изменяются, то отношение давления газа к его абсолютной температуре есть величина постоянная:

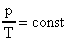(32).

Изохоры, соответствующие двум разным объемам, приведены на рис. 9.

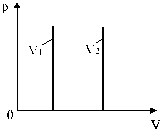
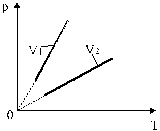
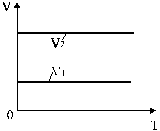
Рис. 9. Изохоры, соответствующие двум разным объемам.

Уравнение изохорического процесса можно записать иначе: 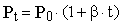(33), где 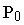- давление газа при 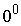С; 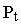- давление газа при t; t - температура газа в градусах Цельсия; 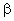- температурный коэффициент давления. Из формулы (33) следует, что 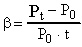. Для всех газов 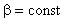и 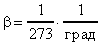. Если газ нагреть на С (при V=const), то давление газа возрастет на 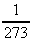часть того давления, которое он имел при С. На рис.10 изображен график зависимости давления газа от температуры t.

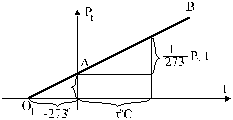
Рис. 10. График зависимости давления газа от температуры t.

Если продолжить прямую AB до пересечения ее с осью x ( точка 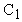), то значение абсциссы этой определиться из формулы (33), если 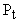приравнять нулю.

;

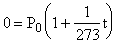
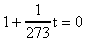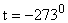
Следовательно, при температуре 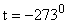давление газа должно было бы обратиться в нуль, однако, при подобном охлаждении газ не сохранит своего газообразного состояния, а обратиться в жидкость и даже в твердое тело. Температура 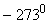носит название абсолютного нуля.

В случае механической смеси газов, не вступающих в химические реакции, давление смеси также определяется формулой 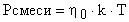, где 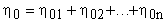(концентрация смеси 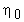равно сумме концентраций компонентов смеси всего n - компонент).

Закон Дальтона гласит: Давление смеси 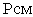равно сумме парциальных давлений газов, образующих смесь. 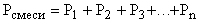. Давления 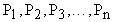называется парциальными. Парциальное давление - это давление, которое создавал бы данный газ, если бы он один занимал тот сосуд, в котором находится смесь (в том же количестве, в котором он содержится в смеси).

СПИСОК ЛИТЕРАТУРЫ

1. Брычков Ю.А., Маричев О.И., Прудников А.П. Таблицы неопределенных интегралов: Справочник. - М.: Наука, 1986.

2. Коган М.Н. Динамика разреженного газа. М., Физматлит, 1999.

3. Кикоин А.К., Молекулярная физика. М., Физматлит, 1976.

4. Сивухин Д.В. Общий курс физики, т. 2. Термодинамика и молекулярная физика. М., Физматлит, 1989.

5. Кирьянов А.П., Коршунов С.М. Термодинамика и молекулярная физика. Пособие для учащихся. Под ред. проф. А.Д. Гладуна. - М., «Просвещение», 1977.

PAGE \* MERGEFORMAT 3

ОПЫТНОЕ ОБОСНОВАНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ