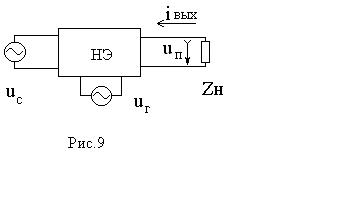
Преобразователи частоты

ЛЕКЦИЯ 4

2.3 Преобразователи частоты

2.3.1 Принципы построения преобразователей частоты

Преобразование частоты представляет собой процесс линейного переноса спектра полезного сигнала по оси частот. Под линейным понимается такой перенос, при котором не изменяется количество спектральных составляющих, расстояние между ними по оси частот, соотношение их амплитуд и начальных фаз. При преобразовании возможно лишь изменение амплитуд гармонических составляющих (увеличение или уменьшение) в одно и тоже число раз и изменение частот этих составляющих (обязательно всех) на одну и туже величину.

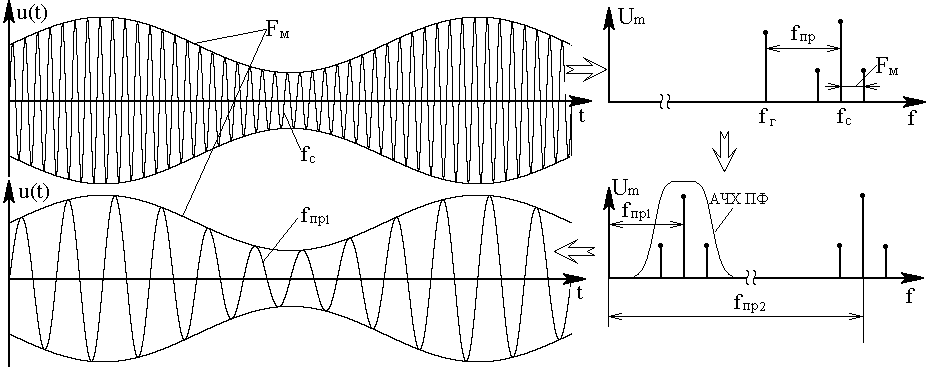
На рис.1 приведен пример изменений тонально - модулированного колебания во временной и частотной областях при преобразовании частоты “вниз”. Из рисунка видно, что полезная информация, которая заключена в амплитуде, начальной фазе и частоте огибающей, при преобразовании частоты не изменилась.

Рис.1

Как видно из рисунка, преобразование частоты связано с появлением в спектре выходного сигнала гармонических составляющих, которых не было в спектре исходного колебания. Как известно, расширение спектра возможно лишь в параметрической либо нелинейной цепи. В связи с этим существует два способа переноса спектра сигнала без нарушения его структуры. Это параметрическое преобразование частоты и преобразование с использованием нелинейного элемента.

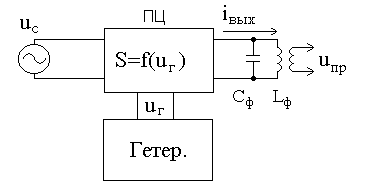
А) Преобразование частоты с помощью параметрической цепи.

Пусть у параметрической цепи (ПЦ на рис.2) под воздействием напряжения гетеродина

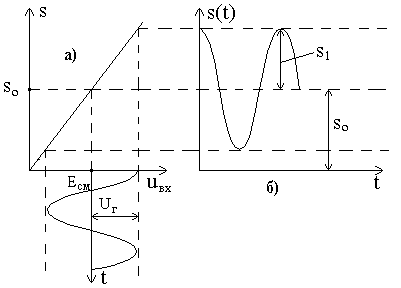
меняется во времени крутизна S(t), связывающая между собой выходной ток и входное напряжение. Закон изменения этого коэффициента во времени (рис.3) будет иметь вид

Рис.2 , (5.1)

где – начальное значение крутизны (при отсутствии гетеродинного напряжения); - первая гармоника крутизны, обусловленная действием гетеродинного напряжения; k - размерный коэффициент пропорциональности.

Если на вход параметрической цепи подать напряжение сигнала, для простоты полагая его равным

,

то выходной ток будет изменяться во времени по закону

(5.2)

Полосовой фильтр (ПФ) LфCф можно настроить как на частоту (разностное преобразование частоты), так и на (суммарное преобразование). Выходное напряжение в первом случае, например, будет иметь вид

, (5.3)

где Кпф - коэффициент передачи ПФ. Объединяя все постоянные величины выражения (5.3) в коэффициент Ко, окончательно можно записать выходное напряжение в виде:

Рис.3 . (5.4)

Как видно из формулы, амплитуда выходного сигнала пропорциональна амплитуде входного, а значит закон ее изменения (при наличии амплитудной модуляции) в процессе преобразования частоты сохраняется.

Б) Преобразователи частоты на базе нелинейного элемента.

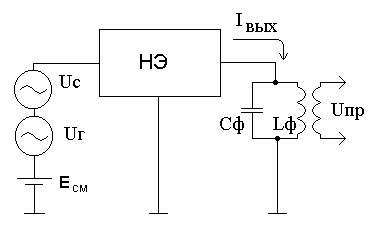
Нелинейным называется элемент, какой либо параметр (параметры) которого зависит от величины воздействующего на него сигнала. Структурная схема преобразователя на базе НЭ изображена на рис.4. Для простоты будем полагать, что зависимость выходного тока от входного напряжения имеет квадратичный характер и описывается выражением

, (5.5)

где к - размерный коэффициент, зависящий от типа параметрической цепи.

Пусть гетеродинное напряжение изменяется по гармоническому закону , (5.6)

а напряжение сигнала, соответственно:,

Рис.4 (5.7)

где - начальная фаза.

Очевидно, что выходной ток будет определяться выражением

(5.8)

Анализ полученного выражения показывает, что в составе выходного тока присутствует постоянная составляющая, величиной

, (5.9)

гармоника на частоте входного сигнала с амплитудой , гармоника на удвоенной частоте сигнала с амплитудой гармоники на частоте гетеродина и удвоенной частоте гетеродина соответственно с амплитудами и . Все эти составляющие не создают падения напряжения на выходном фильтре, настроенном на величину промежуточной частоты .

Выходной сигнал формируется только пятым (), либо шестым () слагаемым из правой части выражения (5.8), в зависимости от того, на какую частоту настроен выходной фильтр. В первом случае напряжение промежуточной частоты описывается выражением:

. (5.10)

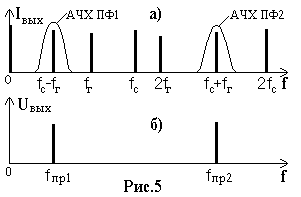
Нетрудно видеть, что здесь, как и в предыдущем случае, амплитуда напряжения промежуточной частоты пропорциональна амплитуде входного сигнала Uc, а значит, закон амплитудной модуляции при преобразовании частоты не нарушается. Сохраняется информация и о фазе полезного сигнала . Спектр выходного тока изображен на рис.5а.

Соответствующей настройкой полосового фильтра можно выделить колебание как суммарной, так и разностной частоты (Рис.5б). Оба варианта используются на практике с учетом конкретных задач преобразования.

До сих пор при рассуждениях предполагалось, что вольтамперная характеристика нелинейного элемента описывается выражением (5.5), т.е. является квадратичной. Характеристики реальных цепей описываются полиномами более высокой степени. Даже при наличии еще только кубического члена в аппроксимирующем полиноме у напряжения гетеродина появятся высшие гармоники, каждая из которых обеспечит в спектре выходного тока пару комбинационных составляющих в соответствии с формулой:

, где n=0,1,2... . (5.11)

Высшие гармоники гетеродинного напряжения появляются и в случае, если само это напряжение имеет форму, отличную от гармонической. И в этом случае частоты на выходе преобразователя будут описываться выражением (5.11). Отсюда вытекает важное требование к гетеродинам. Они должны обеспечивать получение, по возможности, монохроматического колебания.

В реальных преобразователях имеют место обе вышеуказанные причины возникновения комбинационных частот. Иногда, в силу определенных соображений, может специально использоваться преобразование частоты именно на гармониках гетеродина.

Если в ПЧ на нелинейном элементе обеспечить выполнение неравенства

Uc << Uг, (5.12)

то можно будет полагать, что на положение рабочей точки на ВАХ влияет только гетеродинное напряжение. Для рассматриваемого простейшего случая ВАХ, описываемой формулой (5.5), крутизна в текущей рабочей точке будет меняться в соответствии с выражением

и описание работы преобразователя на нелинейном элементе будет аналогично описанию параметрического преобразователя. При выполнении (5.12) нелинейностью участка характеристики, на которую “падает” входной сигнал, можно пренебречь. Чем сильнее неравенство (5.12), тем более линейной по отношению к сигналу можно считать процедуру преобразования частоты. Реальные значения напряжений гетеродинов, подаваемых на ПЧ, лежат в пределах 0,1...2 В. Напряжения сигналов колеблются от долей микровольта в приемниках без УРЧ, до единиц милливольт, т.е. легко обеспечивается оговоренное выше условие.

Особо следует отметить, что гармоники сигнала могут появиться на входе ПЧ и в результате нелинейности характеристик каскадов, предшествующих преобразователю, Такими каскадами являются УРЧ и входная цепь, если в ней для настройки используются, например, варикапы.

Наличие гармоник сигнала в ПЧ приводит к тому, что среди продуктов преобразования присутствуют составляющие на частотах, описываемых более сложным вариантом формулы (5.11):

, (5.13)

где m=0,1,2....- номер гармоники сигнала.

Очевидно, возможны такие комбинации m и n, при которых комбинационная частота становится равной частоте настройки полосового фильтра и такое колебание проходит на выход преобразователя частоты. Это означает, что не только полезный сигнал после преобразования “пересаживается” на промежуточную частоту, но и всякий другой, частота которого удовлетворяет условию, легко получаемому из (5.13)

, (5.14)

где fпр - частота настройки полосового фильтра (промежуточная частота).

Если преобразователь можно считать линейным по отношению ко входному сигналу (m=1), то выражение упрощается:

. (5.15)

Если в (5.14) подставить n = 1 и m = 1, то при одной и той же частоте настройки гетеродина получится пара частот, обеспечивающих после преобразования промежуточную частоту:

. (5.16)

Одна из этих частот называется каналом полезного сигнала, а вторая - зеркальным каналом приема. Зеркальный канал и все остальные, получающиеся из (5.14) при n и m не равных единице, называются побочными каналами приема.

В) Варианты преобразования частоты

На практике находят применение различные варианты преобразования частоты.

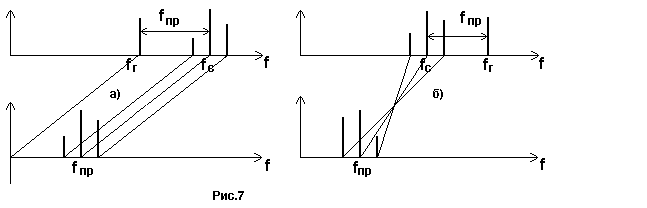
1) Преобразование “вниз”, при котором спектр сигнала перемещается в область частот, лежащую ниже минимальной частоты рабочего диапазона приемника. Преобразование может быть получено только путем вычитания частот сигнала и гетеродина в соответствии с выражением (разностное преобразование). Здесь возможны два варианта: нижняя настройка гетеродина и верхняя . При использовании нижней настройки спектр принимаемого сигнала не инвертируется (рис.7а), а при верхней происходит инверсия боковых спектров (рис7б). Это необходимо учитывать при последующей обработке сигналов, особенно с несимметричными спектрами, например однополосных.

Перенос спектра ниже минимальной частоты диапазона упрощает схему приемника, так как при этом уменьшается количество преобразований частоты, облегчается получение в каскадах, стоящих после преобразователя, высоких коэффициентов усиления и высокой избирательности. Однако при этом затруднено подавление в преселекторе каналов приема на зеркальной и промежуточной частотах.

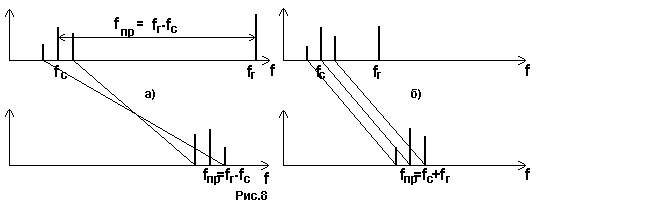
2) Преобразование “вверх”, при котором спектр принимаемого сигнала переносится выше максимальной частоты рабочего диапазона приемника. Преобразование может быть разностным и суммарным (соответственно рис.8а и 8б).

Разностное может быть реализовано только при верхней настройке гетеродина. Как и в предыдущем случае, здесь происходит инвертирование боковых спектров. Недостатком является также необходимость настройки гетеродина на высокие частоты, что требует принятия дополнительных мер по обеспечению его устойчивости. В приемнике, как правило, увеличивается число преобразований частоты, и возникают трудности в изготовлении высокоизбирательных фильтров в тракте первой промежуточной частоты.

Весьма положительным можно считать, при этом, значительное уменьшение коэффициента перекрытия по частоте гетеродина по сравнению с коэффициентом перекрытия по частоте входного сигнала. Действительно, если, например, нижняя частота рабочего диапазона fн=1 МГц, а промежуточная частота fпр=30 МГц, то частота гетеродина должна быть fг=31 МГц. При увеличении частоты гетеродина до 61 МГц (коэффициент перекрытия гетеродина Кп = 61/31 2), верхняя частота рабочего диапазона будет равна fв = 61 - 30 = 31 МГц, а значит коэффициент перекрытия приемника равен 31/1=31, т.е. в пятнадцать раз больше, чем у гетеродина. Легко проверить, что при малых значениях промежуточной частоты эти величины соизмеримы. Коэффициент же перекрытия генератора на практике трудно получить больше 3...5.

Очевидно, существенно при этом упрощается также задача подавления всех побочных каналов приема.

Суммарное преобразование “вверх” может быть реализовано как при верхней, так и при нижней настройках гетеродина.

Нижняя настройка позволяет использовать относительно низкую частоту первого гетеродина. Существенным недостатком здесь является усложнение схемы перестройки, так как для сохранения постоянства промежуточной частоты гетеродин и преселектор должны перестраиваться в противоположных направлениях. Кроме того, увеличивается количество побочных каналов приема, попадающих в рабочий диапазон приемника.

Особенности верхней настройки аналогичны только что описанным, за исключением того, что возникают дополнительные сложности при реализации гетеродина, связанные с необходимостью его настройки на высокие частоты.

2.3.2. Основы теории преобразования частоты

А) Уравнения прямого и обратного преобразования частоты