Расчет простых и сложных цепей постоянного тока

БОУ СПО “Омский колледж проффесиональных технологий”

СРС№2

«Расчет простых и сложных цепей постоянного тока»

Студента группы № 251 Снигерева М.С.

Преподаватель

Евсиков А.С.

Омск-2014

Целью расчёта электрической цепи постоянного тока является определение некоторых параметров на основе исходных данных, из условия задачи. На практике используют несколько методов расчёта простых цепей. Один из них базируется на применении эквивалентных преобразований, позволяющих упростить цепь.

Под эквивалентными преобразованиями в электрической цепи подразумевается замена одних элементов другими таким образом, чтобы электромагнитные процессы в ней не изменились, а схема упрощалась. Одним из видов таких преобразований является замена нескольких потребителей, включённых последовательно или параллельно, одним эквивалентным.

Несколько последовательно соединённых потребителей можно заменить одним, причём его эквивалентное сопротивление равно сумме сопротивлений потребителей, включённых последовательно. Для n потребителей можно записать:

rэ = r1 +r2+…+rn ,

где r1 , r2, ..., rn – сопротивления каждого из n потребителей.

При параллельном соединении n потребителей эквивалентная проводимость gэ равна сумме проводимостей отдельных элементов, включённых параллельно:

gэ= g1 + g2 +…+ gn .

Учитывая, что проводимость является обратной величиной по отношению к сопротивлению, можно эквивалентное сопротивление определить из выражения:

1/rэ = 1/r1 + 1/r2 +…+ 1/rn,

где r1, r2, ..., rn – сопротивления каждого из n потребителей, включённых параллельно.

В частном случае, когда параллельно включены два потребителя r1 и r2, эквивалентное сопротивление цепи:

rэ = (r1 х r2)/(r1 + r2)

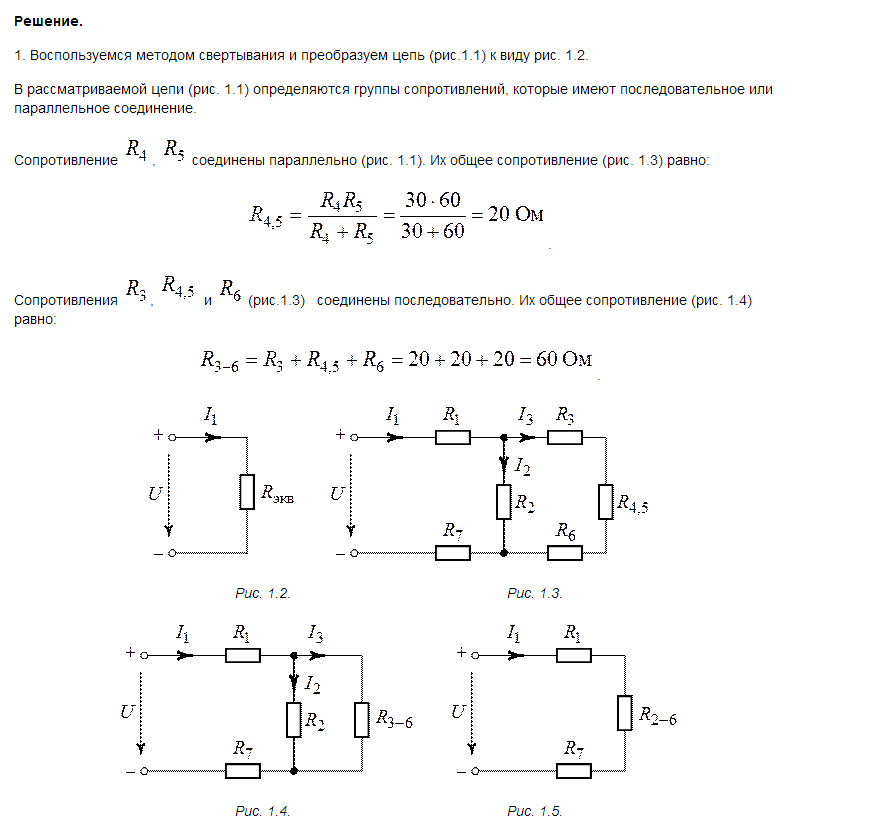
Преобразования в сложных цепях, где отсутствует в явном виде последовательное и параллельное соединение элементов (рисунок 1), начинают с замены элементов, включённых в исходной схеме треугольником, на эквивалентные элементы, соединённые звездой. 

Рисунок 1. Преобразование элементов цепи: а - соединённых треугольником, б - в эквивалентную звезду

На рисунке 1, а треугольник элементов образуют потребители r1, r2, r3. На рисунке 1, б этот треугольник заменён эквивалентными элементами ra, rb, rc, соединёнными звездой. Чтобы не происходило изменение потенциалов в точках a, b, с схемы, сопротивления эквивалентных потребителей определяются из выражений:

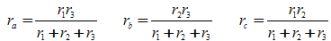
Упрощение исходной цепи можно также осуществить заменой элементов, соединённых звездой, схемой, в которой потребители соединены треугольником.

В схеме, изображённой на рисунке 2, а, можно выделить звезду, образованную потребителями r1, r3, r4. Эти элементы включены между точками c, b, d. На рисунке 2, б между этими точками находятся эквивалентные потребители rbc, rcd, rbd, соединённые треугольником. Сопротивления эквивалентных потребителей определяются из выражений:

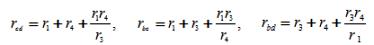
Рисунок 2. Преобразование элементов цепи: а - соединённых звездой, б - в эквивалентный треугольник

Дальнейшее упрощение схем, приведённых на рисунках 1, б и 2, б, можно осуществлять путём замены участков с последовательным и параллельным соединением элементов их эквивалентными потребителями.

При практической реализации метода расчёта простой цепи с помощью преобразований выявляются в цепи участки с параллельным и последовательным соединением потребителей, а затем рассчитываются эквивалентные сопротивления этих участков.

Если в исходной цепи в явном виде нет таких участков, то, применяя описанные ранее переходы от треугольника элементов к звезде или от звезды к треугольнику, проявляют их.

Данные операции позволяют упростить цепь. Применив их несколько раз, приходят к виду с одним источником и одним эквивалентным потребителем энергии. Далее, применяя законы Ома и Кирхгофа, рассчитывают токи и напряжения на участках цепи.

Расчет сложных цепей постоянного тока

В ходе расчёта сложной цепи необходимо определить некоторые электрические параметры (в первую очередь токи и напряжения на элементах) на основе исходных величин, заданных в условии задачи. На практике используются несколько методов расчёта таких цепей.

Для определения токов ветвей можно использовать: метод, базирующийся на основании непосредственного применения законов Кирхгофа, метод контурных токов, метод узловых напряжений.

Для проверки правильности вычисления токов необходимо составить баланс мощностей. Из закона сохранения энергии следует, что алгебраическая сумма мощностей всех источников питания цепи равна арифметической сумме мощностей всех потребителей.

Мощность источника питания равна произведению его ЭДС на величину тока, протекающего через данный источник. Если направление ЭДС и тока в источнике совпадают, то мощность получается положительной. В противном случае она отрицательна.

Мощность потребителя всегда положительна и равна произведению квадрата тока в потребителе на величину его сопротивления.

Математически баланс мощностей можно записать в следующем виде:

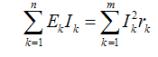
где n – количество источников питания в цепи; m – количество потребителей.

Если баланс мощностей соблюдается, то расчет токов выполнен правильно.

В процессе составления баланса мощностей можно выяснить, в каком режиме работает источник питания. Если его мощность положительна, то он отдает энергию во внешнюю цепь (например, как аккумулятор в режиме разряда). При отрицательном значении мощности источника последний потребляет энергию из цепи (аккумулятор в режиме заряда).

Пацкевич В. А.

Расчет сложной цепи постоянного тока

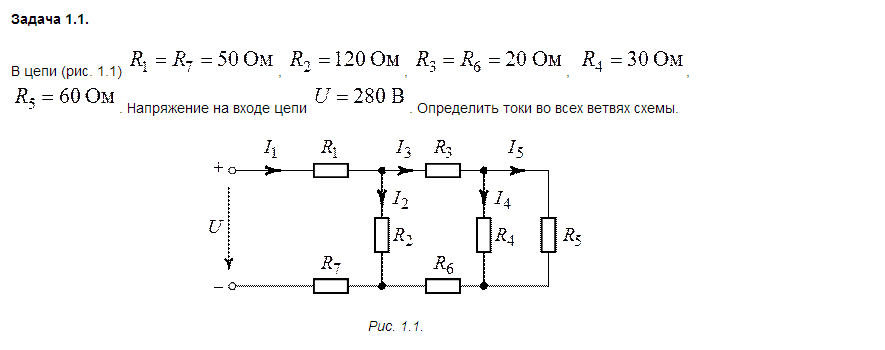
. Электрической цепью обычно называют совокупность электротехнических устройств, образующих некий путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью электрических величин – электродвижущей силы, тока и напряжения. В простейшем случае, расчет электрической цепи заключается в нахождении токов, протекающих через отдельные элементы цепи. При расчете, цепи условно делят на простые и сложные, методики расчета простых и сложных цепей существенно различаются. Любая электрическая цепь содержит ветви и узлы. Ветвь – это участок цепи по которому проходит электрический ток одного значения и направления. Точку электрического соединения трех и более ветвей (или элементов электрической цепи), называют узлом. Простыми электрическими цепями называют цепи с одним источником энергии. Сложной, независимо от количества элементов цепи и последовательности их соединения, считают электрическую цепь, содержащую два и более источника энергии, расположенные в разных ветвях. Законы Кирхгофа При расчете сложной электрической цепи, как правило используют законы Кирхгофа или метод контурных токов, основанный на применении второго закона Кирхгофа. Первый закон Кирхгофа, являющийся уравнением электрического состояния токов для узла и основанный на законе сохранения энергии формулируется так: алгебраическая сумма токов, сходящихся в узле электрической цепи в любой момент времени равна нулю, т.е. k = 0. При этом, токи направленные к узлу, как правило, считают положительными, выходящие из узла, – отрицательными. Второй закон Кирхгофа, являющийся уравнением электрического состояния контура, формулируется так: алгебраическая сумма падений напряжений на элементах замкнутого контура электрической цепи равна алгебраической сумме ЭДС, действующих в данном контуре = , где n – число пассивных элементов в контуре; m – число источников ЭДС. При этом, если направление обхода контура совпадает с направлением тока в элементе – падение напряжения считается положительным, если не совпадает – отрицательным, если направление ЭДС источников совпадает с направлением обхода контура ЭДС считается положительной, если не совпадает – отрицательной. Методика решения задачи при непосредственном применении законов Кирхгофа При решении конкретной задачи может быть рекомендована следующая последовательность действий: 1. проставить произвольно направление токов во всех ветвях электрической цепи; 2. разбить цепи на независимые контура (независимым считается контур не содержащий внутри себя элементов смежных контуров); 3. записать систему уравнений по первому закону Кирхгофа для всех узлов цепи, исключив один узел (какой узел будет исключен, значения не имеет); 4. к составленной системе уравнений добавить контурные уравнения, составленные по второму закону Кирхгофа, число добавленных уравнений должно равняться числу независимых контуров; 5. проверить достаточность количества уравнений – число уравнений должно равняться числу неизвестных токов; 6. решив полученную систему уравнений найти токи во всех ветвях цепи.

Литература (сайты):

http://electricalschool.info/spravochnik/electroteh/698-raschet-jelektricheskikh-cepejj.html

http://vunivere.ru/work14887

PAGE \* MERGEFORMAT1

Расчет простых и сложных цепей постоянного тока