Исследование микромеханического акселерометра на поверхностных акустических волнах

red79;;МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

“Санкт-Петербургский государственный электротехнический университет “ЛЭТИ”

им. В.И. Ульянова (Ленина)” (СПбГЭТУ)

Направление 200100.62

Кафедра ЛИНС

К защите допустить:

Руководитель направления

ВЫПУСКНАЯ

КВАЛИФИКАЦИОННАЯ РАБОТА

БАКАЛАВРА

Тема: Исследование микромеханического акселерометра на поверхностных акустических волнах

Студент		Шкурко Д.В.		/ /
Руководитель		Шевченко С.Ю.		/ /
Зав. кафедрой		Филатов Ю.В.		/ /

Санкт-Петербург

2013 г.

Содержание

Введение…………………………………………………………………………..3

Глава 1. Анализ существующих акселерометров…………………………….10

1. Классификация ММА…………………………………………………….10
   1. По наличию обратной связи……………………………………………..12
   2. По характеру перемещения инерционной массы………………………13
   3. По способу съема выходного сигнала…………………………………..19

Глава 2. Моделирование ЧЭ с прямоугольной формой консоли……………30

Глава 3. Экспериментальные исследования…………………………………..42

3.1. Описание экспериментального макета…………………………………….42

3.2. Градуировка ММА на ПАВ в гравитационном поле Земли…………….44

3.3. Оценка чувствительности микромеханического акселерометра (ММА) к ускорениям больше 1g………………………………………………………….47

3.4. Оценка влияния гравитационных сил на чувствительный элемент (ЧЭ) ММА при действии ускорения ортогонально оси чувствительности……….51

Заключение……………………………………………………………………….54

Литература……………………………………………………………………….55

Введение

На сегодняшний день одним из важнейших направлений развития микросистемной техники является разработка микромеханических датчиков и систем. Микромеханические акселерометры (ММА) –перспективные приборы современной микросистемой техники, интенсивно и динамично развивающегося научно-технического направления. Микромеханические акселерометры характеризуются уникально малыми массой и габаритами, низким потреблениям электроэнергии, возможностью функционирования в жестких условиях эксплуатации и на несколько порядков меньшей стоимостью, чем их традиционные аналоги. Определенные перспективы открываются при переходе к специфическому классу приборов и систем, использующих свойства поверхностных акустических волн (ПАВ) в пьезоэлектриках. Их основным элементом являются линии задержки и резонаторы, свойства которых зависят от измеряемых параметров движения. Исключительная простота кинематической схемы и высокий уровень конструктивной интеграции создают предпосылки для повышения точностных характеристик, уменьшения общих габаритов и существенного уменьшения общей стоимость их производства. Поэтому разработка датчиков на ПАВ представляется актуальной.

Целью работы является оценка характеристик микромеханического акселерометра на поверхностных акустических волнах.

Объектом исследования является микроакселерометр на ПАВ.

Для достижения поставленной цели в дипломной работе необходимо решить следующие задачи:

1. Анализ существующих микроакселерометров.
2. Градуировка ММА на ПАВ в гравитационном поле Земли.
3. Оценка влияния ускорения на смещение частоты ПАВ-резонатора.

1. Оценка чувствительности микромеханического акселерометра (ММА) к ускорениям больше 1g.
2. Оценка влияния гравитационных сил на чувствительный элемент (ЧЭ) ММА при действии ускорения ортогонально оси чувствительности.

Акселерометры реагируют на ускорение, действующее на чувствительный элемент датчика. Ускорение, статическое или динамическое, возникает под действием силы, ускоряющей датчик, например, вследствие действия гравитации. Следовательно, акселерометры могут применяться для измерения силы, ускорения, вибрации, движения или перемещения, а также положения и угла наклона. Линейка однокристальных интегральных акселерометров компании Analog Devices Inc. (ADI), выполненных по технологии iMEMS, покрывает практически все области применения устройств подобного типа —от систем управления автомобильными подушками безопасности до сотовых телефонов [1].

Области применения акселерометров определяются их основными параметрами, а также их соотношением. Важнейшими параметрами акселерометра являются диапазон измеряемых ускорений, чувствительность, выражаемая обычно как отношение сигнала в вольтах к ускорению, нелинейность в процентах от полной шкалы, шумы, температурные дрейфы нуля (смещения) и чувствительности. Благодаря этим качествам они нашли свое применение во множестве отраслей:

• военная и гражданская авиация;
• автомобилестроение;
• аэрокосмическое приборостроение;
• робототехника;
• военная промышленность;
• нефтяная и газовая промышленность;
• спорт;
• медицина.

В ряде случаев существенной характеристикой оказывается собственная частота колебаний сенсора 0 или резонансная частота 0, определяющая рабочую полосу частот датчика. В большинстве применений важны температурный диапазон и максимально допустимые перегрузки —характеристики, связанные с условиями эксплуатации датчиков.

Определяющими параметрами, влияющими на точность определения ускорения, являются дрейфы нуля и чувствительности (в основном температурный), а также шумы датчика, ограничивающие порог разрешения устройства. Чувствительность датчика зависит от резонансной частоты механической подсистемы, а также качества электронного преобразователя.

Изменение чувствительности с температурой связано в основном с изменением коэффициента упругости. Температурный дрейф нуля обусловлен изменением коэффициента упругости, тепловым расширением и технологическими погрешностями изготовления сенсора. Изменение параметров электронной части датчика под действием температуры, как правило, существенно меньше.

Поскольку акселерометр измеряет ускорение или силу, вызывающую ускорение инерционной массы, физическая модель акселерометра представляет собой инерционную массу, подвешенную на пружине, закрепленной в неподвижном корпусе, - простую систему с одной степенью свободы x в направлении измерительной оси (рис.а). Инерционная масса приобретает ускорение под действием ускоряющей силы (равнодействующей силы инерции при воздействии ускорения), пропорциональной массе m и ускорению a:

F = ma. (1)

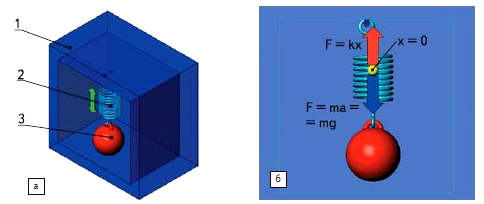
Рис. 1. Физическая модель акселерометра:

а –конструкция физической модели: 1 –неподвижный корпус; 2 –пружина, закрепленная в корпусе; 3 –инерционная масса; б –силы, действующие на модели.

Сила упругости (жесткости) пружины в этой модели уравновешивает перемещение инерционной массы m относительно корпуса:

F = kx, (2)

где k –жесткость пружины, х –перемещение массы относительно исходной точки.

Из формул (1) и (2) следует, что

а = x(k/m),

где k/m –конструктивный параметр датчика.

В соответствии с данной моделью в основе классификации акселерометров лежит различие в способах получения электрического сигнала при детектировании движения инерционной массы.

Согласно физической модели (рис. 1) функциональное назначение акселерометра и линейность предполагают получение линейной передаточной характеристики —зависимости выходного напряжения от детектируемого ускорения преимущественно в аналоговом или ШИМ-формате (рис. 2).

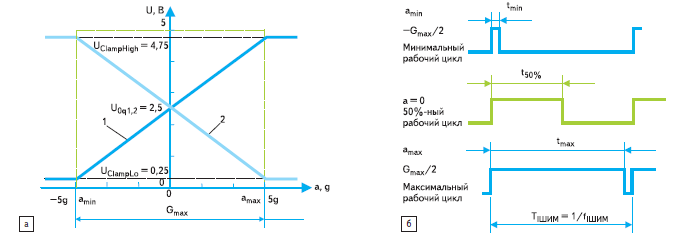
Рис. 2. Передаточные характеристики акселерометра: а —линейная выходная характеристика: а, g —детектируемое ускорение; amin, amax —амплитудные значения колебаний ускорения; Gmax = amin + amax —максимальный диапазон; U —выходное напряжение; UClampHigh, UClampLo —ограничивающие уровни; U0q —среднеквадратическое напряжение; 1 —униполярная выходная характеристика; 2 —инвертированная униполярная выходная характеристика; б —ШИМ-выходная характеристика: a —детектируемое ускорение; amin, amax —амплитудные значения колебаний ускорения; Gmax —максимальный диапазон; tmin, t50%, tmax —длительности импульсов (tmin — минимальная длительность при минимальном ускорении, t50% —длительность импульса, соответствующая 50%-ному рабочему циклу при нулевом ускорении, tmax —максимальная длительность при максимальном ускорении); ТШИМ и fШИМ —постоянные значения периода и частоты ШИМ-сигнала.

В соответствии с данным определением основными рабочими характеристиками акселерометров принимаются:

• максимально детектируемый диапазон ускорений a (полная шкала) Gmax, равный пиковому размаху детектируемых амплитудных значений amax и amin;
• динамический диапазон амплитуды —отношение максимального диапазона измерений к шумам;
• чувствительность —изменение выходного сигнала, например аналогового напряжения, за единицу изменения в ускорении:

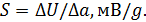
• среднеквадратическое напряжение U0q —среднее из ограничительных уровней выходного сигнала UClampLow, UClampHigh (аналогично определяется среднеквадратический рабочий цикл);
• смещение нуля —отклонение по оси выходного сигнала (U), соответствующее нулевому значению ускорения (0g);
• дрейф чувствительности —вариации чувствительности, не являющиеся функцией измеренной переменной, например в зависимости от температуры T, отличной от комнатной температуры (температурный дрейф).
• дрейф смещения —отклонение среднеквадратического напряжения U0q от теоретического значения в полном диапазоне, например вследствие влияния температуры T по сравнению с температурой в 25 °C.
• нелинейность —максимальное отклонение выхода от идеально прямой линии графика ускорения в зависимости от выхода, выраженное в процентах от полной шкалы.
• рабочий частотный диапазон ;
• резонансная частота 0 или ;
• разрешение —самый малый уровень g, который способен измерить акселерометр (преимущественно определяемый шумами и рабочей шириной полосы частот);
• число измерительных осей;
• поперечная осевая чувствительность —процентное выражение поперечного ускорения (или действующего под углом 90°), отображаемого на выходе акселерометра (у идеального акселерометра поперечная чувствительность равна нулю);
• масса (малая в сравнении с детектируемой системой);
• рабочий температурный диапазон T;
• чувствительность к акустическим шумам;
• коэффициент демпфирования (затухания колебаний).

Глава 1. Анализ существующих акселерометров.

1. Классификация ММА.

При построении современных микромеханических акселерометров используются те же концепции, которые уже отобраны на их микроаналогах, однако их конструктивная реализация, определяемая особенностями микротехнологий, имеет принципиальные отличия.

При всем имеющемся многообразии современных ММА концепции их построения можно условно разделить на несколько основных групп по признакам, которые приведены на рис. 3. [2]

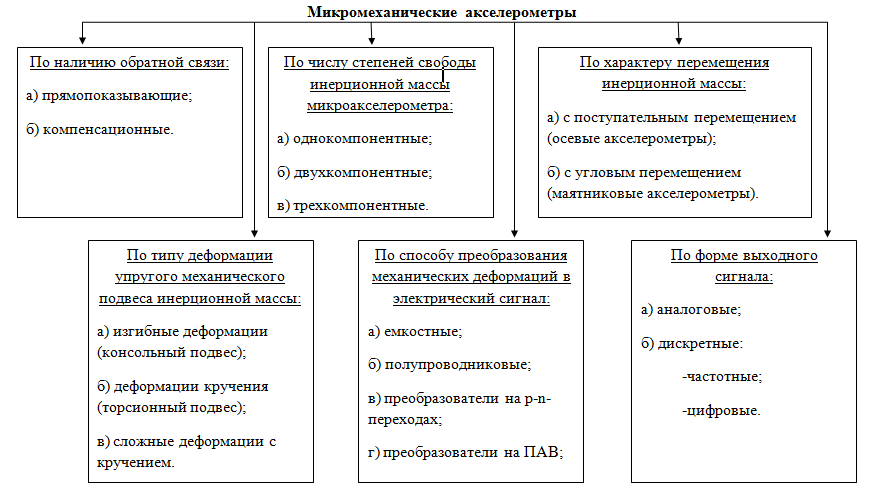
1. По наличию обратной связи.

Компенсационные (с обратной связью)

В этих приборах осуществляется автоматическое уравновешивание силы инерции ЧЭ другой силой, которую можно создать и измерить с необходимой точностью. Акселерометры подобного типа представляют собой измерительную систему с отрицательной обратной связью, которая позволяет уменьшить значение относительной погрешности.

Рассмотрим структурную схему компенсационного акселерометра, показанную на рис. 4.

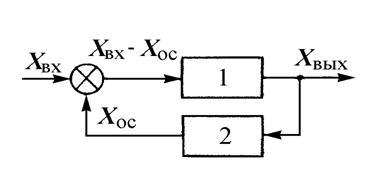
Рис. 4. Структурная схема компенсационного акселерометра.

На ней акселерометр 1 охвачен отрицательной обратной связью. Передаточный коэффициент системы запишем в виде:

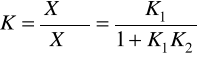, (3)

где K1 и K2 - передаточные коэффициенты звеньев прямой и обратной связи соответственно.

Если на выходах звеньев 1 и 2 имеются погрешности X1 и X2, то при отсутствии входного сигнала (Xвх = 0) результирующая погрешность на выходе

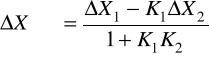. (4)

Разделив левую и правую части уравнения (4) на Xвых , получим величину относительной ошибки:

,

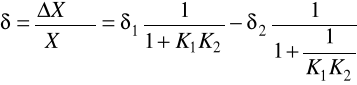где К1 = X1/Xвых; К2 = X2/Xос - относительные погрешности звеньев 1 и 2.

Соответствующим выбором коэффициентов K1 и K2 можно управлять значением результирующей ошибки . Обеспечив K1K2 >>1, получим –2.

Таким образом, ошибка прямого канала (звено 1) оказалась исключенной, а суммарная ошибка теперь определяется только ошибкой канала обратной связи (звено 2), которую в общем случае можно сделать достаточно малой.

Сразу же отметим, что уменьшение результирующих ошибок акселерометра достигается ценой снижения его чувствительности, которая пропорциональна коэффициенту передачи акселерометра. Из выражения (3) видно, что всегда K < K1, т. е. в компенсационной схеме коэффициент передачи акселерометра уменьшается при введении отрицательной обратной связи.

1. По характеру перемещения инерционной массы (ИМ).

а) Маятниковый акселерометр

Конструктивная схема микромеханического акселерометра маятникового типа приведена на рис. 5, инерционная масса с опорным элементом и торсионами на рис. 6.

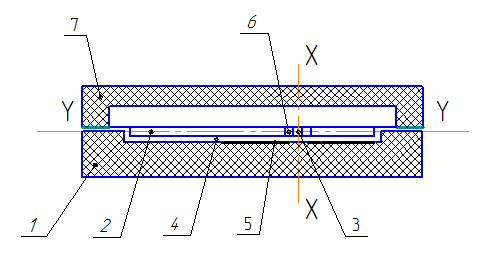
Рис. 5 Конструктивная схема микромеханического акселерометра

маятникового типа:

1 –корпус; 2 –инерционная масса; 3 –торсионы; 5 –неподвижные электроды; 6 –опорный элемент; 7 –диэлектрическая крышка.

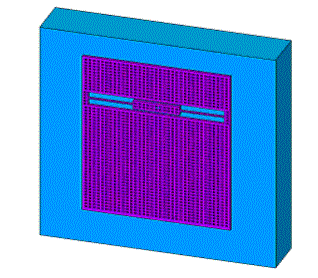
Рис. 6 Пространственная модель инерционной массы.

Микромеханический акселерометр представляет собой капсулированный элемент, образованный корпусом 1, выполненным в виде платы из диэлектрического материала с напыленными на ней неподвижными электродами 5 емкостного датчика угла и электростатического датчика момента и диэлектрической крышки 7. Крышка скреплена с корпусом 1.

Основой акселерометра является монокристаллический кремневый элемент –маятник размерами 0,8x1,0x0,015. Инерционная масса 2 подвешена с зазором на плате в виде маятника на упругих перемычках –торсионах 3 за опорный элемент 6. Торсионы представляют собой устройство демпфирования сечением 12х15 мкм, которое позволяет инерционной массе останавливаться при полном диапазоне колебаний, защищая устройство от механического удара. Инерционная масса, торсионы и опорный элемент выполнены в форме прямоугольника, на поверхности которого равномерно распределены сквозные отверстия.

Напыленные электроды емкостного датчика угла и электростатического датчика моменты выполнены единым элементом и в совокупности представляют собой электронную схему обработки сигналов.

Рассматриваемое устройство работает следующим образом. При действии ускорения в направлении оси чувствительности Х-Х инерционная масса 2 отклоняется от своего исходного состояния. При этом изменяются величины емкостей конденсатора, образованного неподвижными электродами 5 и инерционной массой 2. Съем информации производится с помощью емкостного датчика перемещений. Сигнал отклонения преобразуется электронной схемой и приводит к возникновению электростатического момента, стремящегося возвратить инерционную массу 2 в исходное состояние. В установившемся состоянии сигнал с выхода электронной схемы является выходным сигналом микромеханического акселерометра.

График зависимости перемещения чувствительного элемента маятникового типа от преобразуемого им линейного ускорения приведен на рисунке 7.

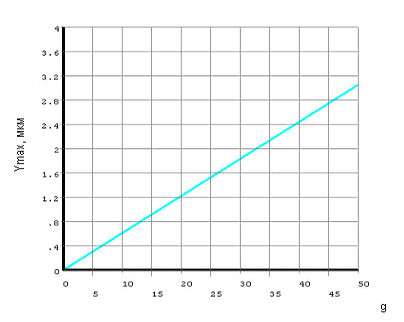
Рис. 7. График зависимости перемещения инерционой массы акселерометра маятникового типа от воздействия линейного ускорения.

б) Осевой акселерометр

Данный акселерометр относится к устройствам для измерения ускорения объекта в условиях вибрации и может быть использовано для контроля положения подвижного объекта.

Конструктивная схема чувствительного элемента осевого типа, представлена на рисунке 8. Пространственная модель представлены на рисунке 9.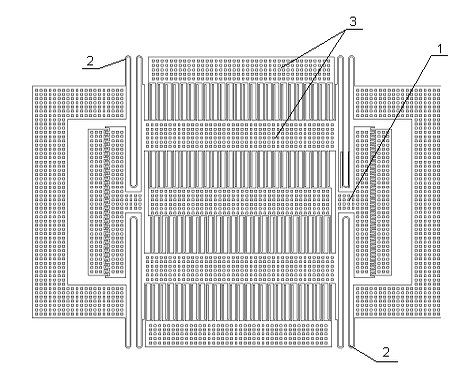

Рис. 8. Конструктивная схема ММА осевого типа.

–инерционная масса; 2 –торсионы; 3 –неподвижные пластины.

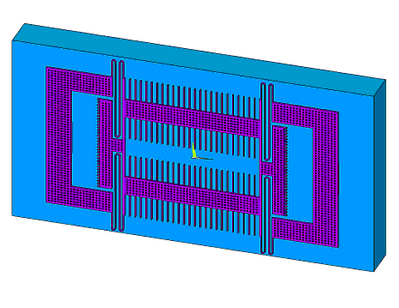
Рис.9. Пространственная геометрическая модель чувствительного элемента.

Чувствительный элемент относится к типу акселерометров с поступательным перемещением чувствительной массы. Он представляет собой пластину, изготовленную из монокристаллического кремния – инерционная масса 1, толщиной 15 мкм и размерами в плоскости подвеса 0,5х1,0 мм, расположенную с зазорами относительно корпуса, подвешенную к нему на четырех упругих торсионах 2. В результате образуется упругий подвес, обеспечивающий перемещение инерционной массы вдоль оси, лежащей в плоскости инерционной массы. Съем информации производится по дифференциальной схеме с помощью гребенчатого емкостного датчика перемещений. 

Рассматриваемое устройство работает следующим образом. При действии ускорения в направлении оси чувствительности Х-Х инерционная масса 1 отклоняется от своего исходного состояния. Сигнал, снимаемый с датчика перемещений, приводит к возникновению электростатических сил, стремящихся возвратить инерционную массу 1 в установившееся положение. В установившемся состоянии сила инерции, действующая на инерционную массу, уравновешивается электростатическими силами гребенчатого датчика силы.

График зависимости перемещения инерционной массы осевого типа от амплитуды воздействующего линейного ускорения приведен на рисунке 10.

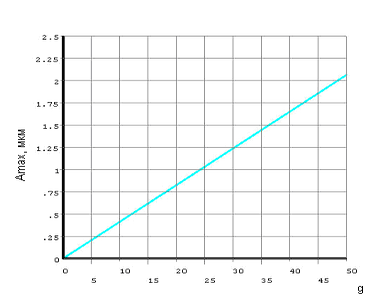
Рис. 10. График зависимости перемещения инерционной массы осевого типа от амплитуды воздействующего ускорения линейного.

1. По способу съема выходного сигнала.

а) Емкостные

Емкостные датчики используются для решения широкого круга задач —этот тип устройств позволяет определять положение, перемещение, ускорение и многие другие параметры. Применение емкостной технологии в автоэлектронике ассоциируется именно с акселерометрами, которые получили наиболее широкое распространение благодаря их высокой чувствительности, стабильности при детектировании статического ускорения, малого дрейфа, низкой температурной чувствительности, малой потребляемой мощности, высокой надежности, хорошим шумовым свойствам, удовлетворительному разрешению и точности, низкой цене.

Принцип действия емкостного акселерометра основан на изменении емкости чувствительного элемента с электродами при перемещении инерционной массы, являющейся его частью, под действием ускорения.

Большинство МЭМС-акселерометров использует принцип, в котором ускорение изменяет расстояние d между обкладками и, таким образом, емкость конденсатора. Датчик преобразует изменение емкости акселерометра в выходной сигнал —электрический заряд, напряжение или ток.

Типичный емкостный элемент состоит из двух фиксированных элементов –между ними подвешена подвижная обкладка, нагруженная инерционной массой, которая представляет собой общий электрод емкостного полумоста (рис. 11, а – г).

Рис. 11. Измерительный принцип дифференциального емкостного акселерометра: а, б –физическая модель измерительной структуры: 1, 3 –неподвижные металлические обкладки; 2, 4 –зафиксированные печатные платы; 5 –подвижная обкладка; 6 –инерционная масса; 7, 8 –слои диэлектрика; S –фиксированная площадь перекрытия обкладок; d1, d2 –переменные расстояния между обкладками; а –акселерометр в состоянии покоя; б –под действием ускорения а; в –эквивалентная электрическая схема; г –размещение измерительных осей и степеней свободы относительно корпуса ИС.

г) Преобразователи на p-n-переходах.

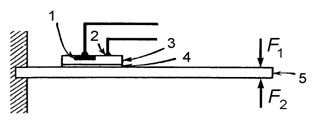
Рис. 12. Тензометр на туннельном диоде.

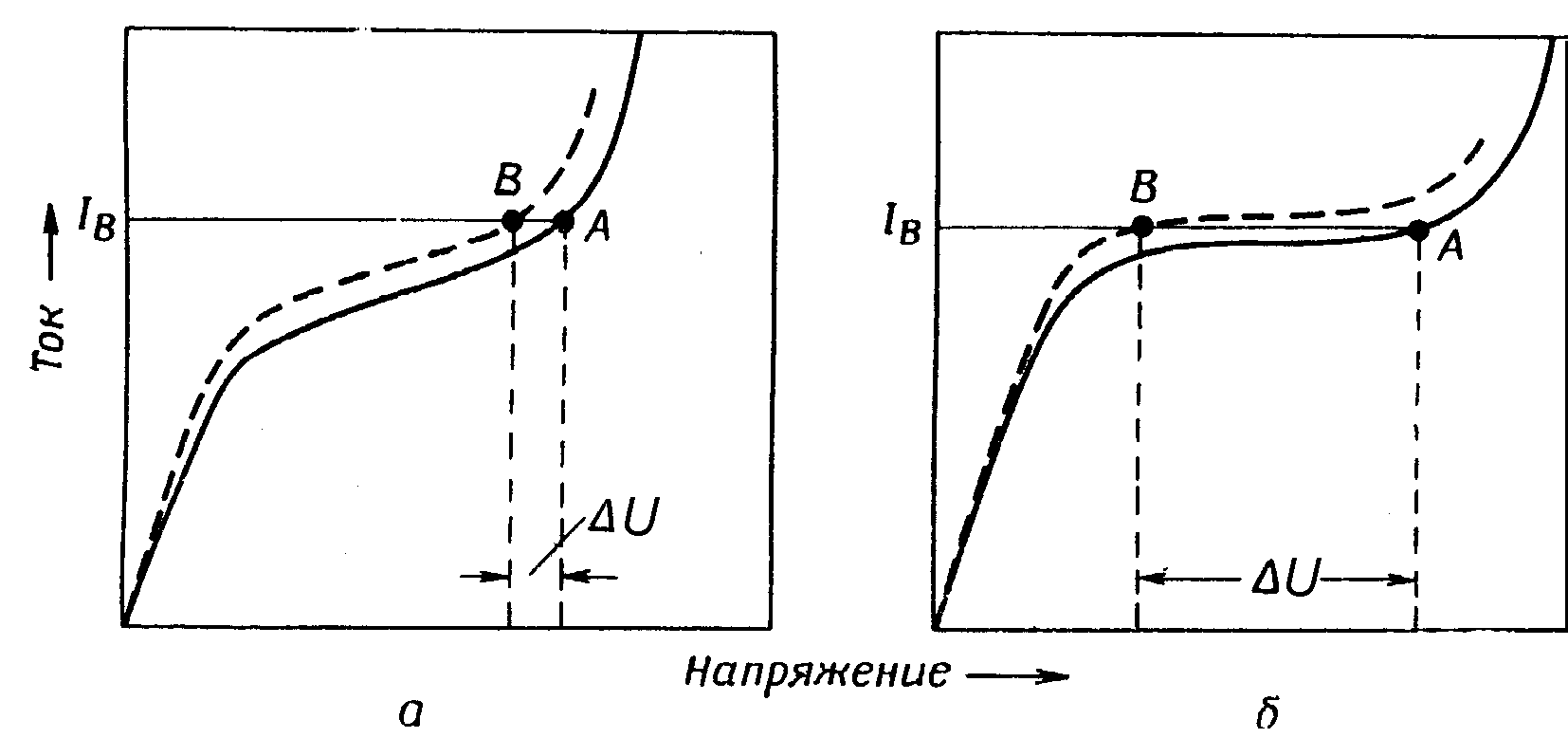
На рис. 12 представлен тензодатчик с туннельным диодом и омическим контактом, смонтированный на консольной балке. Туннельный p-n-переход получен путем вплавления кончика проволоки из алюминия с добавкой 1% бора в пластинку из кремния. Кремниевая пластинка вырезана и укреплена на консоли таким образом, что вплавление производится на плоскость, соответствующую кристаллографической плоскости. Кремний легирован сурьмой до концентрации 5·1019 атомов в см3. Тензодатчик прикреплен к консольной балке из бериллиевой бронзы эпоксидной изолирующей смолой. Для питания устройства используется источник постоянного тока. Когда на консоль действует сила F1, p-n-переход туннельного диода подвергается одноосному растяжению в плоскости перехода. Аналогично при приложении силы F2 переход испытывает одноосное напряжение сжатия. В результате воздействия этих напряжений вольт-амперная характеристика диода изменяется.

Чувствительность туннельного диода к силовой нагрузке может быть повышена, если использовать участок вольт-амперной характеристики с отрицательным сопротивлением. Это можно осуществить, если шунтировать диод сопротивлением Rш при условии

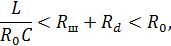
где R0 – отрицательное сопротивление диода, С – емкость перехода, Rd – внутреннее последовательное сопротивление диода, L – индуктивность всей схемы.

Работа тензодатчика с туннельным диодом в режиме усиления объяснена на рис. 13.

Рис. 13. Принцип действия тензометра с туннельным диодом: а - большая разность между Rш и R0 соответствует малой чувствительности, б - малая разность между Rш и R0 соответствует высокой чувствительности к деформации.

Рис. 13, а соответствует шунтирующему сопротивлению Rш = 600 Ом, а рис. 13, б –сопротивлению 1100 Ом. Отрицательное сопротивление диода в данном случае R0 = 1220 Ом. Следовательно, разность между шунтирующим сопротивлением и отрицательным сопротивлением диода составляет 50 и 10% соответственно. Если на диод подано смещение, соответствующее рабочей точке А на рис. 13, а, и создана деформация за счет приложения силы F1 (рис. 12), то характеристика принимает новую форму, показанную пунктирной кривой. При этом точка смещения переходит из положения А в положение В и напряжение на диоде изменяется на U. При шунтирующем сопротивлении Rш = 1100 Ом (рис. 13, б) средняя часть вольт-амперной характеристики шунтированного диода имеет значительно меньший наклон.

Как и в предыдущем случае, деформация вызывает перемещение рабочей точки из А в B, но теперь изменение напряжения U будет большим, и поэтому измерение деформаций может производиться с большей чувствительностью. Деформация S вычисляется по формуле (, с, a и l указаны на рис. 14):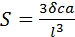

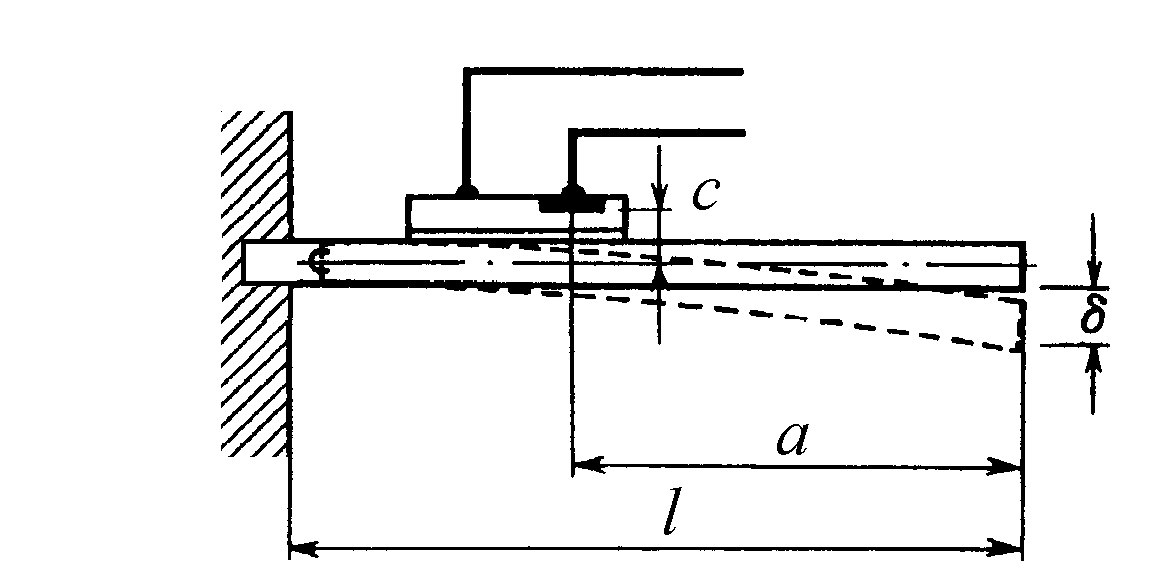
Рис. 14. Схема с указанием величин, необходимых для вычисления деформации в тензометрах с р-n-переходами, смонтированных на консольной балке.

На рис. 15 показан тензодатчик с двумя туннельными переходами 1, образованными на противоположных сторонах стержня из полупроводникового материала 2. Эти переходы включены в два плеча моста Уитстона для увеличения чувствительности устройства. При воздействии на полупроводниковый стержень силы F один из переходов подвергается растяжению, а другой –сжатию.

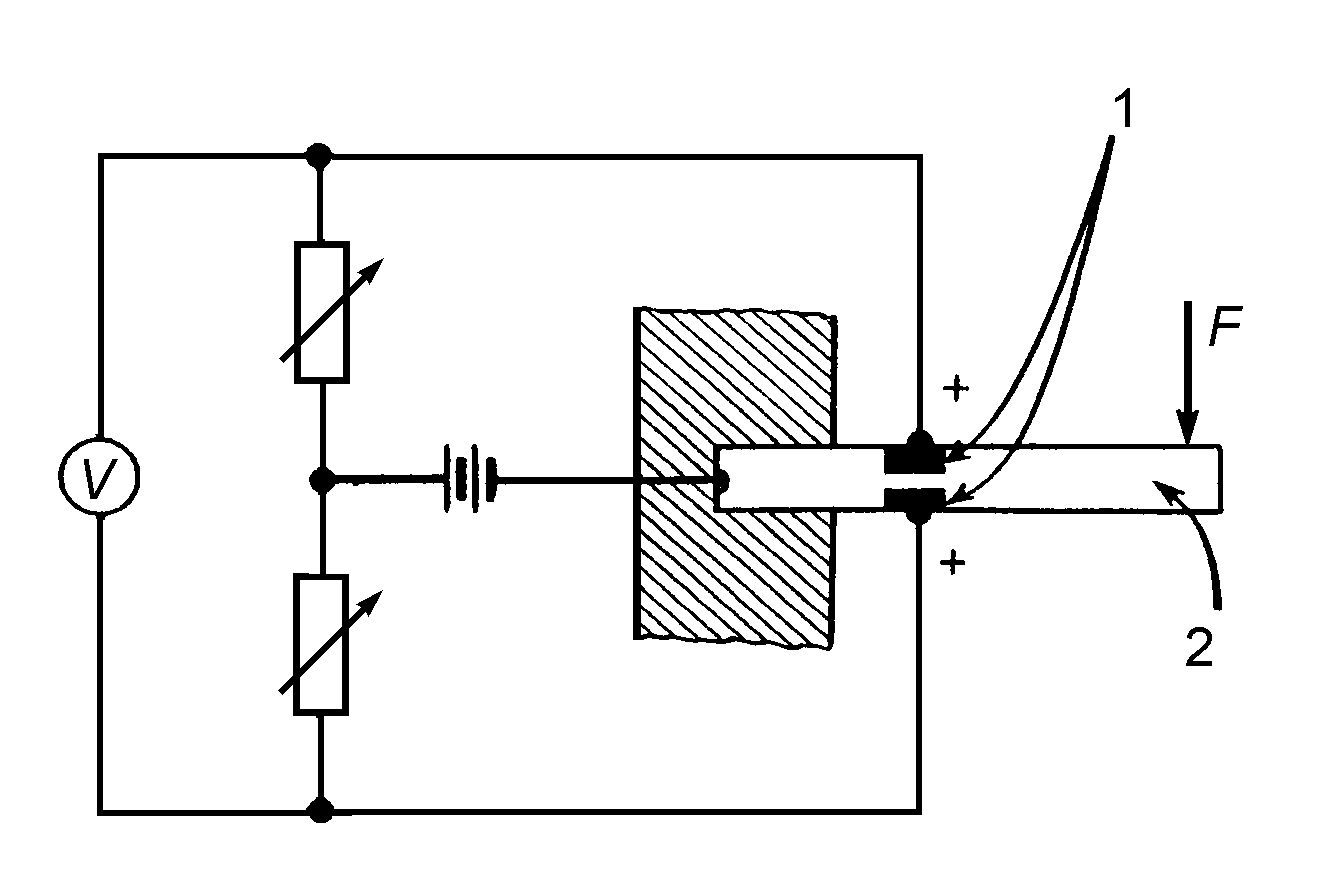
Рис. 15. Тензодатчик с двумя туннельными переходами.

Электрический сигнал на выходе удваивается по сравнению с сигналом, получаемым при использовании только одного перехода.

г) Струнные

Струнные преобразователи, изучаемые в данной работе, применяются для относительных измерений линейных размеров в диапазоне до 200 мкм. Основной областью их применения является контроль геометрических параметров изделий в машиностроении.

Принцип действия струнных преобразователей основан на использовании зависимости частоты собственных поперечных колебаний струны от ее продольного натяжения.

Для идеально гибкой струны, жестко закрепленной с обоих концов, эта частота определяется следующим выражением:

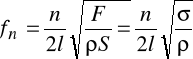, (5)

где 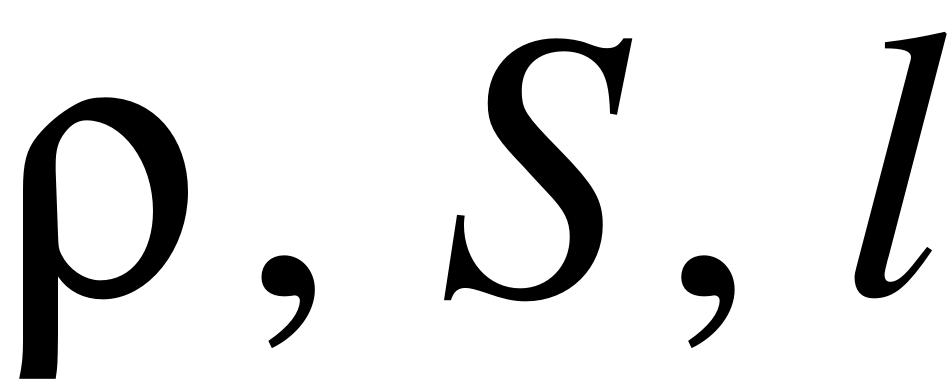– плотность, площадь поперечного сечения и длина струны, – механическое напряжение в струне, 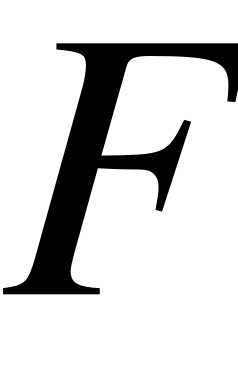– сила продольного натяжения струны, 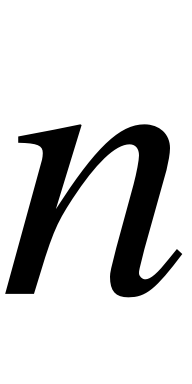– номер гармоники колебаний (как правило, используется возбуждение колебаний на первой гармонике).

При расчете преобразователей повышенной точности или при отношении длины струны к ее толщине, меньшем 300 необходимо учитывать влияние поперечной жесткости струны. В этом случае выражение для определения частоты собственных поперечных колебаний может быть записано следующим образом:

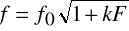, (6)

где

.

В приведенных выражениях: 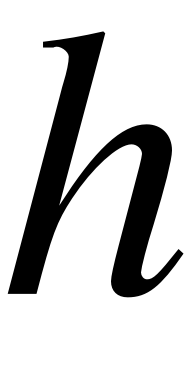–толщина струны, 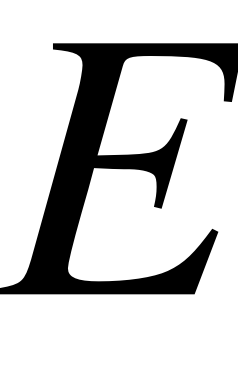–модуль продольной упругости (модуль Юнга), –плотность материала струны, 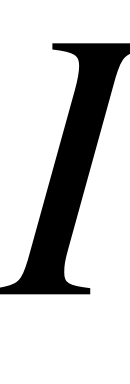–осевой момент инерции поперечного сечения. Произведение представляет собой жесткость при изгибе.

Для измерения частоты собственных поперечных колебаний струны ее помещают в постоянное магнитное поле (рис. 16). Колебания струны вызывают возникновение в ней ЭДС, при этом частота переменного напряжения на концах струны будет соответствовать частоте ее поперечных колебаний. Для возбуждения и поддержания колебаний в струне используются струнные автогенераторы.

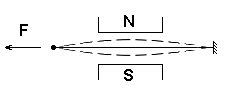
Рис. 16. Натянутая струна в постоянном магнитном поле

Сущность метода заключается в том, что измеряемая физическая величина либо непосредственно, либо через цепь предварительных преобразователей приводит к изменению силы натяжения струны, а, следовательно, к изменению частоты ее поперечных колебаний.

Изменение частоты колебаний струны ведет к изменению частоты электрического сигнала, соответственно входной величиной струнного ИП является продольно действующая сила, вызывающая натяжение струны, а выходной – частота электрического сигнала, проходящего по струне.

Наиболее простым и часто используемым способом измерения частоты собственных поперечных колебаний струны является включение струнного преобразователя в качестве частотозадающего элемента автогенератора (рис. 17).

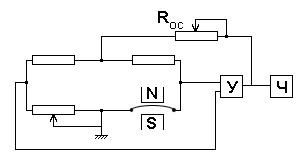
Рис. 17. Струнный автогенератор

Формирование выходного сигнала автогенератора происходит следующим образом:

1. Колебания струны в поле постоянных магнитов приводят к возникновению ЭДС;
2. Переменное напряжение с диагонали моста подается на электронный усилитель (У);
3. С выхода усилителя через резистор обратной связи (Rос) на вершину моста подается ток подкачки для поддержания колебаний струны;
4. Частотомером (Ч) производится измерение частоты колебаний электрического сигнала на выходе преобразователя.

Таким образом, входным сигналом для струнного преобразователя является продольно действующая сила, растягивающая струну, а выходным –частота колебаний автогенератора.

Основным недостатком описанного выше преобразователя является нелинейность статической характеристики (это следует из выражений (5) и (6)). Для устранения этого недостатка используют дифференциальную схему измерения, т.е. включение двух идентичных струн так, чтобы при изменении измеряемой величины натяжение одной из них усиливалось, а второй –уменьшалось. Добиться этого можно, используя Т-образный рычаг (рис. 18).

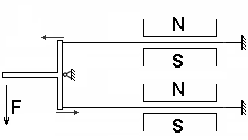
Рис. 18. Дифференциальный струнный преобразователь с Т-образным рычагом

Выходной величиной такого преобразователя чаще всего является разность или отношение частот. Это позволяет получить функцию преобразования с относительно большим (по сравнению с однострунным преобразователем) линейным участком.

д) Преобразователи на ПАВ-резонаторах.

Схема чувствительного элемента (ЧЭ), применяемого в микроакселерометрах данного типа, представлена на рис. 19.

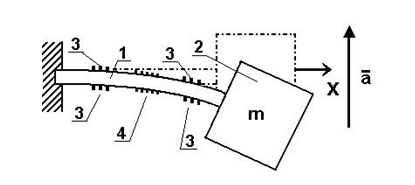
Рис. 19. Схема ЧЭ микроакселерометра:

–консоль; 2 –инерционная масса;

3 –отражатели ПАВ-резонатора; 4 –ВШП

При воздействии ускорения 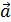консоль 1, нагруженная массой 2, испытывает деформации изгиба, которые сопровождаются растяжением и сжатием ее противоположных поверхностей. На них нанесены резонаторы, образованные отражателями 3 и встречно-штыревыми преобразователями 4.

Возникающие деформации приводят к изменению собственных частот резонаторов. На верхней части пластины они увеличиваются как за счет геометрического удлинения консоли, так и за счет уменьшения фазовой скорости, вариации которой определяются изменением упругих модулей (их уменьшением). На противоположной стороне имеют место деформации сжатия, которые приводят к противоположному сдвигу собственной частоты резонатора.

Таким образом, получаем двухканальную схему, которая соответствует дифференциальному преобразователю частотного типа. Частотозадающими элементами в нём являются одновходовые ПАВ-резонаторы. Изменение их разностной частоты пропорционально приложенному ускорению.

Глава 2. Моделирование ЧЭ ММА на ПАВ с прямоугольной

формой консоли.

Микромеханические датчики инерциальных систем навигации и управления находят все более широкое применение на подвижных объектах различного класса гражданского и военного применения. Успехи в развитии методов и средств производства изделий микроэлектроники позволили создать необходимую базу для разработки и массового выпуска акселерометров (ММА), которые получили название твердотельных.

Твердотельные ММА  используют набор дискретных упругих подвесов, обеспечивающих необходимые степени свободы инерционным элементам. Эти обстоятельства ограничивают виброустойчивость и ударопрочность микрочувствительных элементов, с одной стороны, и требуют использования сложных объемных технологий, с другой.

Определенные перспективы открываются при переходе к специфическому классу приборов и систем, использующих свойства поверхностных акустических волн в пьезоэлектриках. Их основным элементом являются линии задержки и резонаторы, свойства которых зависят от измеряемых параметров движения. Простота кинематической схемы и высокий уровень конструктивной интеграции создают предпосылки для повышения точностных характеристик, уменьшения общих габаритов и существенного уменьшения общей стоимость их производства. Поэтому разработка датчиков на ПАВ представляется актуальной.

2.1. Уравнение движения ЧЭ ММА

Для выбора параметров ЧЭ необходимо детальное изучение напряженно-деформированного состояния консоли и оценка распределения поверхностных деформаций по ее длине. Соответствующая расчетная схема представлена на рис. 20.

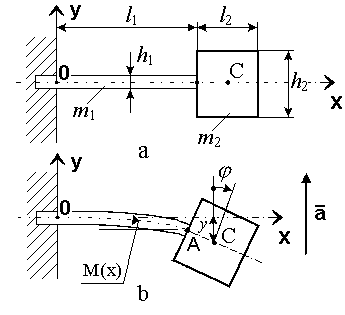
Рис. 20. Расчетная схема чувствительного элемента

микроакселерометра.

Для расчета дифференциальных уравнений движения чувствительного элемента введем следующие обозначения: 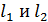продольные и 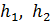поперечные размеры консольной балки и инерционной массы, соответственно; b ширина консоли; 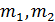массы балки и инерционного элемента, закрепленного на ее конце, соответственно; 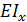изгибная жесткость балки, E модуль упругости материала балки; 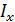момент инерции сечения балки; 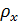радиус инерции инерционной массы относительно центра масс. За обобщенные координаты рассматриваемой системы примем прогиб y и угол поворота консоли , как показано на рис. 20b. Для дальнейших расчетов принимаем, что удовлетворяется условие .

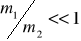Рассмотрим сначала модель чувствительного элемента, пренебрегая массой 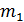по сравнению с инерционной массой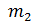. При составлении дифференциальных уравнений движения чувствительного элемента используем способ, получивший в теории колебаний название обратного способа составления дифференциальных уравнений движения.

Он заключается в том, что отделяются сосредоточенные массы и рассматривается оставшаяся безынерционная система, находящаяся под действием кинематических реакций отдельных частей системы. Причем кинетические реакции (силы инерции) выражаются через обобщенные ускорения. Дифференциальные уравнения движения рассматриваемой системы при принятых допущениях будут иметь вид:

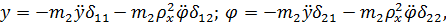
где 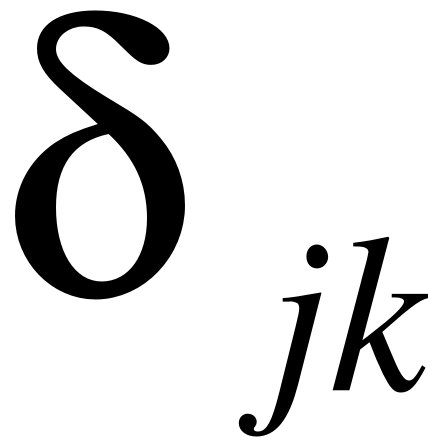обозначены коэффициенты влияния, которые, следуя работе [5], можно представить в форме:

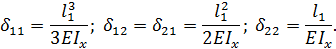
Таким образом, дифференциальные уравнения движения ЧЭ микроакселерометра принимают вид:

;

.

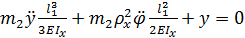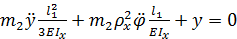При действии ускорения подложка ЧЭ, выполненного, например, в форме консоли, нагруженной инерционной массой, испытывает деформации сжатия, растяжения или изгиба. Это приводит к изменению ее геометрических размеров, упругих констант и плотности, ответственных за вариации скорости ПАВ, что, в свою очередь, влечет изменение собственной частоты резонатора или времени пробега вдоль линии задержки. Для консоли из кварца степень влияния этих факторов приведена на рис. 21.

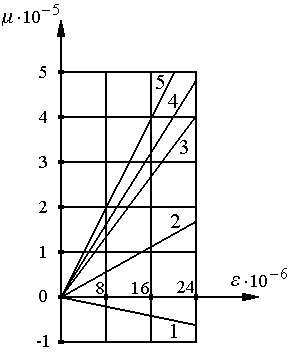
Рис. 21. Влияние относительных деформаций на скорость ПАВ:

1 - вклад изменения плотности материала, 2 - вклад изменения расстояния, 3 - вклад изменения скорости ПАВ, 4 - вклад изменения модулей упругости, 5 - результирующее изменение времени распространения.

Вследствие деформаций, вызванных действующим ускорением, изменяется топология отражателей и ВШП. Вклад этого фактора в изменение фазы и частоты ПАВ зависит от структуры резонатора или линии задержки и может быть довольно существенным. Таким образом, структура поля поверхностной акустической волны существенным образом зависит от напряженно-деформированного состояния подложки. Поэтому в каждой конкретной схеме построения ЧЭ на ПАВ необходим тщательный анализ распределения поверхностных напряжений, относительных поверхностных удлинений и собственных колебаний упругой конструкции ЧЭ.

Изменение знака напряжения (переход с растяжения на сжатие) изменяет знаки всех компонент. Это создает необходимые предпосылки для построения дифференциальной схемы МА. С этой целью на каждой из поверхностей консоли размещаются одновходовые ПАВ-резонаторы, как показано на рис. 18. Общая топология и эквивалентная схема ПАВ-резонатора приведены на рис. 22a и 22b, соответственно.

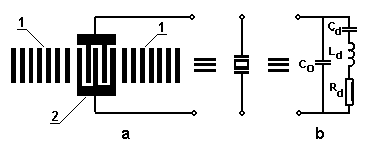
Рис. 22. Топология (a) и эквивалентная схема ПАВ-резонатора (b):

–отражатели резонатора, 2 –ВШП.

Такая структура имеет минимальное количество выводов и может быть наиболее просто включена в контур автогенератора. Анализ эквивалентной схемы ПАВ-резонатора показывает, что динамические параметры Rd, Ld, Cd шунтируются паразитной статической емкостью Cо. В результате создаются условия для существования последовательного fs и параллельного fp резонансов. Разнос между ними определяется соотношениям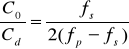и

и ,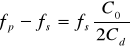

и составляет, как правило, очень небольшую величину, которая зависит от добротности резонаторов: с её увеличением происходит сближение частот. Поэтому при разработке автогенераторов на ПАВ-резонаторах необходимо принимать серьёзные меры для исключения “перескоков” частоты.

В свою очередь, собственные частоты резонаторов определяются расстоянием между отражателями, их дисперсионными свойствами и скоростью распространения ПАВ. Резонансную частоту невозмущенного резонатора f0 можно найти из соотношения

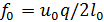
где u0 невозмущённое значение фазовой скорости ПАВ, q >> 1 целое число, l0 –длина невозмущенного резонатора (расстояние между эффективными центрами отражения рефлекторов) или

,

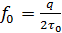где 0 –время распространения ПАВ на длине l0.

Тогда выражение для собственных частот резонаторов (f1, f2) и их разности при действии ускорений на ЧЭ микроакселерометра может быть записано в виде

,

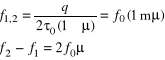где - среднее значение относительных изменений времени распространения ПАВ в зоне размещения элементов резонатора под действием механических напряжений. Знаки соответствуют противоположным по знаку приращениям частот, обусловленных деформациями растяжения и сжатия.

Вследствие этого, при проектировании микроакселерометров на ПАВ необходимо оценивать распределение механических напряжений по длине подложки и относительные удлинения слоев подложки, на которых расположены резонаторы.

Принцип построения автоколебательной системы с частотно-задающим резонатором представлен на рис. 23.

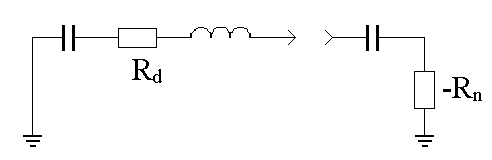
Рис. 23. Эквивалентная схема автогенератора с ПАВ-резонаторами.

Здесь собственные потери резонатора Rd компенсируются отрицательным сопротивлением – Rn, которое создается активной схемой, например, усилителем.

Обобщенная структурная схема дифференциального ПАВ-акселерометра показана на рис. 24. Она включает консольный ЧЭ с двумя ПАВ-резонаторами 1 в цепи автогенераторов 2, смеситель 3 и два фильтра 4, 5.

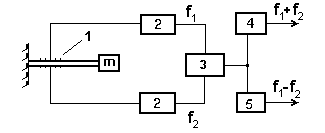
Рис. 24. Структурная схема ПАВ-акселерометра:

1 –ПАВ-резонаторы, 2 –автогенераторы, 3 –смеситель, 4, 5 –фильтры выделения суммарной и разностной частоты.

Гармонические колебания двух автогенераторов 2 поступают на смеситель 3, где происходит формирование сигналов с комбинационными частотами f1f2. Разностная частота f1f2 оказывается пропорциональной действующему ускорению, а суммарная частота f+f может быть использована для уменьшения влияния дестабилизирующих факторов и, прежде всего, температуры через канал автоподстройки частот генераторов.

Для исключения взаимной синхронизации двух автогенераторов собственные частоты одновходовых резонаторов, нанесенных на опозитные стороны консоли, разносятся на некоторую фиксированную частоту, величина которой обычно лежит в диапазоне 100..500 кГц. Однако при массовом производстве ПАВ-резонаторов не удается выдержать необходимые значения номиналов невозмущенных резонансных частот с точностью лучше 50 кГц. В связи с этим возникает необходимость индивидуальной подстройки собственных частот резонаторов f10 и f20 к значениям, обеспечивающим паспортную величину начального разноса частот f0=f10-f20. Эта задача может быть решена двумя путями:

• непосредственной коррекцией параметров резонаторов сразу после их изготовления, т.е. до сборки акселерометров, используя, например, лазерные технологии;
• электронной подстройкой частот генерации f10 и f20 осцилляторов в уже полностью собранном ПАВ-акселерометре.

Первый путь требует применения специальных технологических операций, дорогостоящей оснастки и больших временных затрат, что ведет к увеличению стоимости изделия и не гарантирует достижения нужных параметров в уже корпусированном акселерометре. Поэтому предпочтение следует отдать построению осцилляторных схем с управляемой напряжением перестройкой частоты, например, на основе варикапов конденсаторов, управляемых напряжением. В этом случае варикап включается в контур резонатора и осуществляет его перестройку в небольшом диапазоне частот вблизи резонансных значений f10 и f20. Характер зависимости перестройки частоты автогенератора от приложенного напряжения приведен на рис. 25.

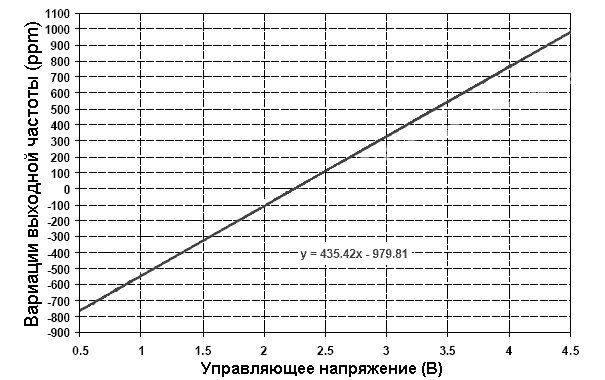
Рис. 25. Зависимость выходной частоты от управляющего напряжения.

Крутизна характеристики составляет 43510-6 1/B при вариациях управляющего напряжения 0.3..3 В. Такой диапазон перестройки почти на порядок перекрывает технологические погрешности изготовления ПАВ-резонаторов и гарантирует необходимую выставку начального разноса частот осцилляторов уже после окончательной сборки и корпусирования акселерометров. Предложенная схема на базе варикапа может быть также использована для компенсации температурных воздействий.

В работе рассматриваются результаты моделирования консоли чувствительного элемента микроакселерометра на ПАВ при нанесении на ее поверхности пленок различной топологии. Для моделирования используется программный комплекс ANSYS Workbench, в основе вычислений которого лежит метод конечных элементов (МКЭ).

На сегодняшний день во многих микродатчиках используются чувствительные элементы (ЧЭ) консольного типа. При воздействии на них измеряемой величины происходит изменение формы консоли, которое переводится в электрический сигнал при помощи преобразователей, размещенных на ее гранях. Очевидно, что характер изгиба консоли и распределение поверхностных напряжений непосредственно влияют на характеристики датчика. [3] Рассмотрим это на примере микромеханического акселерометра (ММА) на поверхностных акустических волнах (ПАВ). Основной целью является оценка деформации ЧЭ под действием ускорения.

2.2. Аналитический метод решения

ЧЭ ММА на ПАВ представляет собой консоль, жестко закрепленную с одной стороны и нагруженную инерционной массой (ИМ) с другой (рис. 26).

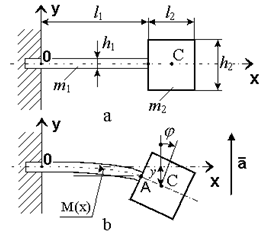
Рис. 26. Расчетная схема чувствительного элемента ММА.

При воздействии ускорения консоль испытывает деформации изгиба, которые сопровождаются растяжением и сжатием ее противоположных поверхностей. На них нанесены ПАВ-резонаторы, которые включены в цепь положительной обратной связи усилителя. Их собственные частоты приобретают противоположные по знаку приращения частот, что позволяет реализовать дифференциальный метод измерения.

В работе [4] приведен вывод выражений для внутренних напряжений и относительных деформаций, возникающих под действием ускорения. Для расчета введены следующие обозначения (рис. 26): 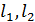продольные и  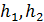 поперечные размеры консоли и ИМ, соответственно; b ширина консоли; 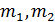массы консоли и ИМ, соответственно; 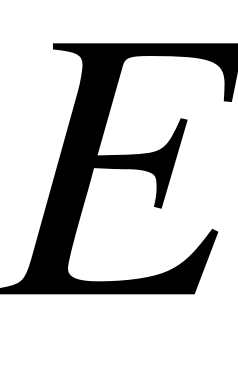модуль упругости материала консоли (кварц ST-среза). Принимая условие 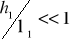получаем конечные выражения для максимальных нормальных напряжений 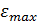и относительных удлинений на поверхности консоли:

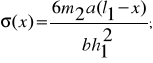
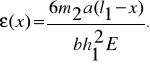
Приведенные формулы не учитывают массу самой консоли, анизотропию ее материала, прорези в ИМ для крепления консоли и др. Компьютерное моделирование позволяет избавиться от большинства имеющихся в аналитическом методе допущений.

2.3. Оценка влияния ускорения на смещение частоты ПАВ-резонатора.

В программе ANSYS Workbench была построена трехмерная модель ЧЭ ММА на ПАВ, которая была разбита на конечные элементы прямоугольной сеткой с шагом 0,175 мм для консоли и 0,5 мм для ИМ. В качестве материала консоли был выбран кварц, а для ИМ –сплав ВНМ.

В качестве внешнего воздействия задавалось равномерно распределенное ускорение свободного падения, направленное вдоль оси y (рис.26). Один конец консоли был жестко закреплен, а другой нагружен ИМ. Результаты моделирования приведены на рис. 27. Распределение относительных деформаций на оппозитных сторонах консоли –на рис. а). График 2, б) более наглядно демонстрирует распределение относительных деформаций вдоль оси симметрии ЧЭ.

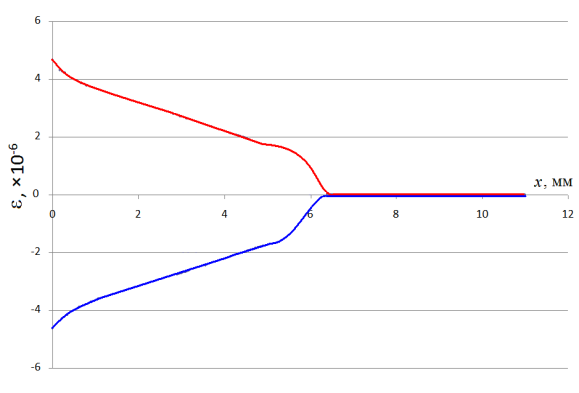
а) б)

Рис. 27. Результаты моделирования ЧЭ ММА на ПАВ с прямоугольной консолью.

Как видно из рис. 27 б, распределение относительных деформаций по длине консоли является неоднородным. В случае несимметричного расположения ПАВ-резонаторов это приводит к различной чувствительности плеч дифференциальной схемы и, следовательно, дополнительным погрешностям. Существующие технологии не позволяют добиться необходимой точности взаимного размещения ПАВ-резонаторов при массовом производстве. Поэтому необходимо найти такую форму консоли, которая обеспечила бы равномерное сопротивление изгибу по всей длине [7].

Далее был произведен пересчет значений 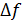согласно формуле:

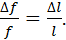
Полученные данные приведены в таблице №1 и №2.

Таблица №1.Вдоль оси чувствительности:

Ускорение, g	0,5		,5		,5		,5
Относительная деформация, 10-5	1,38	,76	,14	,52	,9	,28	,66
Смещение, кГц	12

Таблица №2. Ортогонально оси чувствительности:

Ускорение, g	0,5		,5		,5		,5
Относительная деформация, 10-13	0,74	,48	,22	,95	,69	,43	,17	,91
Смещение, мкГц	480

По данным таблицы №1 можно видеть, что при действии ускорения 1g, смещение частоты происходит примерно на 24 кГц. То есть, если при 0g выходная частота составляет 467 кГц, тогда при 1g –значения 467 кГц и 24кГц складываются или вычитаются (в зависимости от направления); и в итоге на выходе частота составит примерно или 491 кГц или 443 кГц.

Глава 3. Экспериментальные исследования.

3.1. Описание экспериментального макета.

Установка представляет собой одноосную мини-центрифугу, разработанную на кафедре ЛИНС. На план-шайбе установлен макет микромеханического акселерометра 1 (рис. 29), подключенный к источнику питания PSM-6003 2 (задающее питание –,5 В), частотомеру METEX MXC-260 3, электронному блоку 4 и компьютеру 5 (рис. 28).

Рис. 28. Экспериментальная установка:

1 –миницентрифуга с ММА; 2 –блок питания; 3 –частотомер; 4 –электронный блок; 5 –компьютер.

Рис. 29. Макет ММА

Далее представлена электрическая схема ПАВ-микроакселерометра (рис. 30).

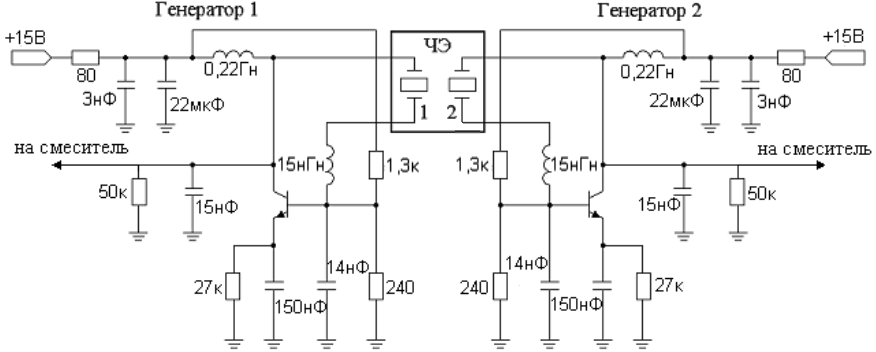
Рис. 30. Электрическая схема ПАВ-микроакселерометра с прямоугольной формой консоли ЧЭ

Схема состоит из двух автономных генераторов, собранных на транзисторах 2T-640A2 и ПАВ-резонаторах 1 и 2. Выходные сигналы первого и второго генераторов подаются на вход смесителя, в качестве которого была использована микросхема SCM-1 фирмы Mini-Circuits. Она обеспечивает повышенную развязку между генераторами (около 40 дБ) и позволяет в ряде случаев отказаться от дополнительных развязывающих усилительных каскадов между автогенераторами. Область взаимной синхронизации двух автогенераторов (зона захвата) составляет менее ± 12 кГц и полностью избавиться от нее не удается. Эффективным решением подобной проблемы является перенос рабочей точки частотного ММА в область, удаленную от зоны захвата. С этой целью собственные частоты ПАВ-резонаторов, расположенных на противоположных поверхностях ЧЭ, разносятся в процессе их изготовления на значительную величину порядка 500 кГц, которая существенно превышает диапазон возможных минимальных значений разностной частоты. Однако современные методы тонкопленочной технологии, используемые ведущими отечественными и зарубежными производителями ПАВ-резонаторов, показывают, что предельная точность настройки каждого отдельного резонатора может варьироваться от ± 50 кГц до ± 150 кГц в используемом диапазоне частот около 435 МГц. Практически, после корпусирования ЧЭ начальный разнос частот генераторов изменяется в более широких пределах.

3.2. Градуировка ММА на ПАВ в гравитационном поле Земли.

Градуировка ММА с прямоугольной формой консоли в гравитационном поле Земли выполнялась на центрифуге. Съем выходного сигнала ММА производился через каждые 10° в диапазоне от 0° до 360° в направление по часовой стрелке и против нее. По полученным данным построены графики градуировки (см. рисунок 32) и выходной характеристики ММА (см. рисунок 31), найдены масштабный коэффициент и сдвиг нуля: по часовой стрелке – Км = 25,0 кГц/g и K0 = 473,5 кГц, против часовой стрелки –Км = 25,3 кГц/g и К0=477,0 кГц. Так же рассчитан коэффициент нелинейности, который составил: по часовой стрелке - Кн = 4,1 %; против часовой стрелки –

Кн=3,8 %. При проведении экспериментальных исследований было выявлено большое время выхода на рабочий режим (см. рисунок 33), которое составило более часа. Причиной этого явления является значительное тепловыделение как на элементах электрической схемы (резисторы, транзисторы и др.).

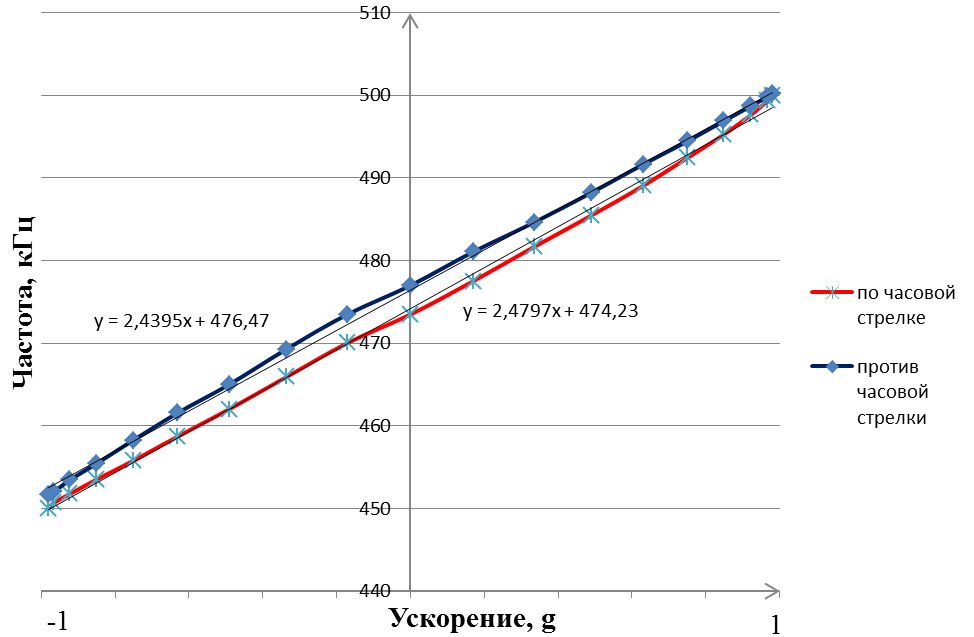
Рис. 31. Выходная характеристика ПАВ-микроакселерометра в гравитационном поле Земли.

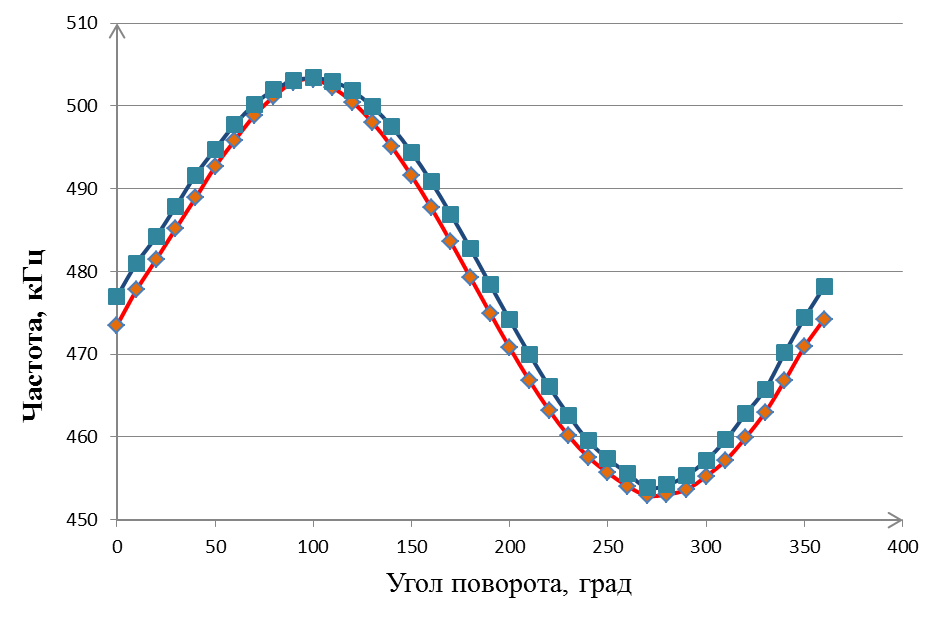
Рис. 32. Градуировка ПАВ-микроакселерометра в гравитационном поле Земли.

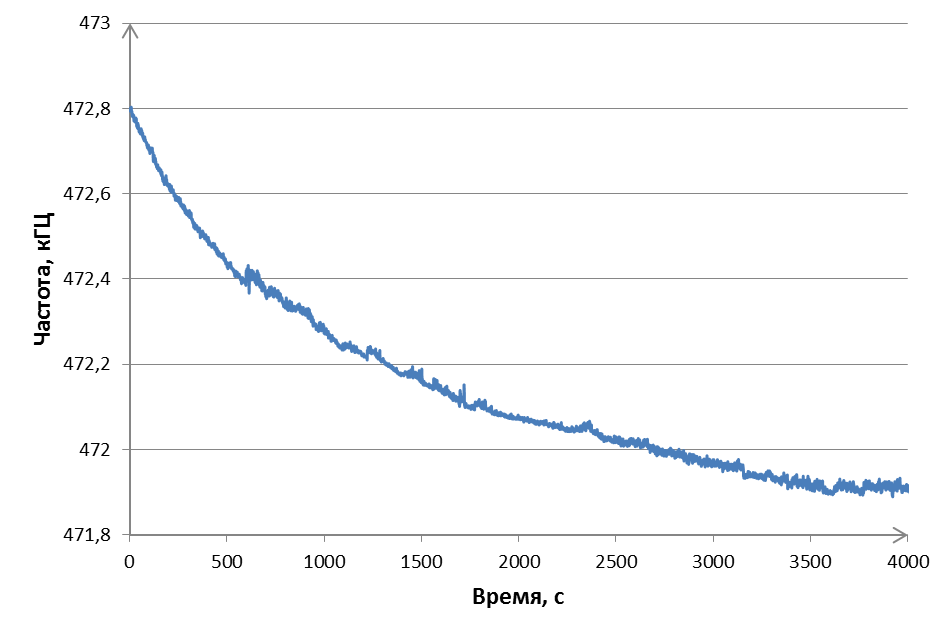
Рис. 33. Время выхода ПАВ-микроакселерометра на рабочий режим.

3.3. Оценка чувствительности ММА к ускорениям больше g.

Следующим этапом исследований стала оценка чувствительности ММА к ускорениям больше g. Для проведения испытания так же использовалась мини-центрифуга, которая позволяла задавать различные значения угловой скорости в диапазоне от 0 до 240 °/мин в обоих направлениях. Механический акселерометр устанавливался на некотором расстоянии от центра, R=0,065 м. Съем выходного сигнала ММА производился через каждые 10 об/мин в диапазоне от 0 об/мин до 240 об/мин в направление по часовой стрелке и против нее. По полученным данным построены графики градуировки (рис. 34, 36) и выходной характеристики (рис. 37, 35). Так же был произведен расчет масштабного коэффициента. Для случая, когда инерционная масса расположена сверху, при 1g - Км = 22,1 кГц/g и при 4g – 23,8 кГц/g.

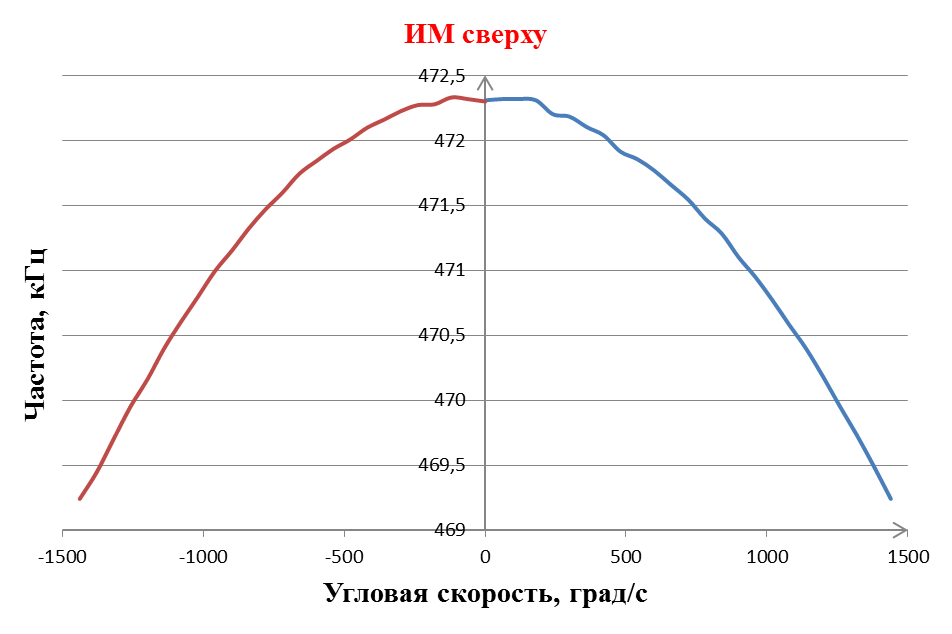
Рис. 34. Градуировка ПАВ-микроакселерометра при расположении ИМ сверху.

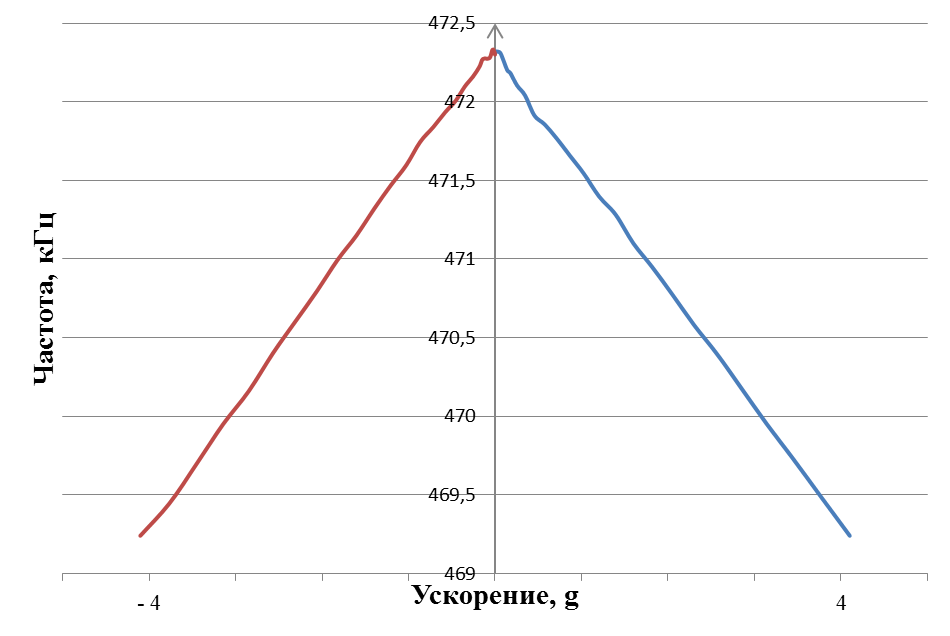
Рис. 35. Выходная характеристика ПАВ-акселерометра при расположении ИМ сверху.

При расположении инерционной массы снизу при 1g масштабный коэффициент составляет 21,2 кГц/g, а при 4g –23,4 кГц/g.

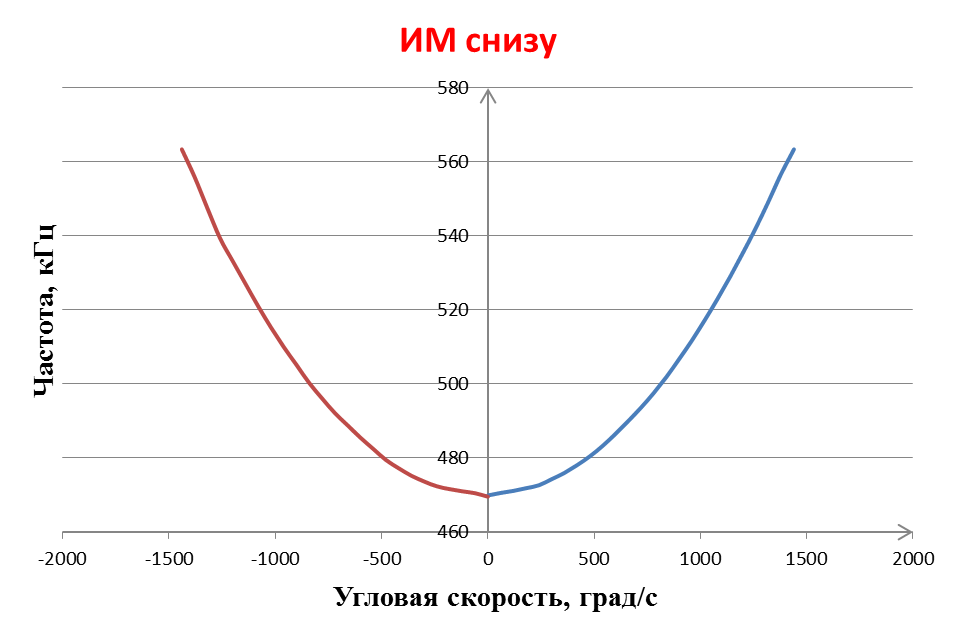
Рис. 36. Градуировка ПАВ-микроакселерометра при расположении ИМ снизу.

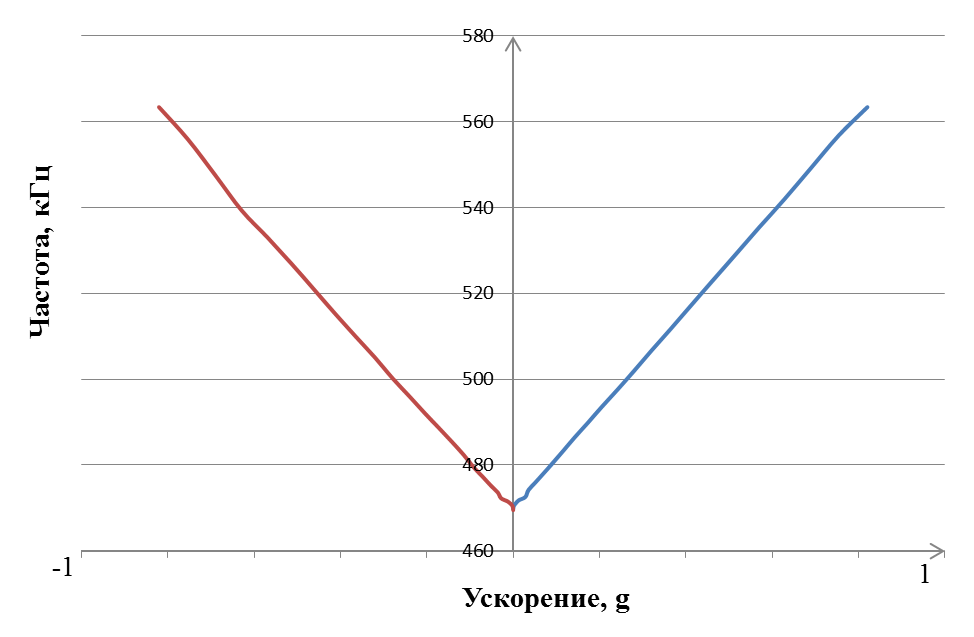
Рис. 37. Выходная характеристика ПАВ-микроакселерометра при расположении ИМ снизу.

3.4. Оценка влияния гравитационных сил на чувствительный элемент ММА при действии ускорения ортогонально оси чувствительности.

В следующем этапе исследования требовалось получить зависимость выходного сигнала микроакселерометра от ускорения силы тяжести ортогонально оси чувствительности. Шаг изменения угла поворота составлял 10° в диапазоне от 0° до 360°. Для этого, в первом случае, консоль располагалась ортогонально оси чувствительности (на рисунках показаны красным цветом), во втором случае –сонаправленно (на рисунках показаны синим цветом).

Было выявлено, что микроакселерометр наиболее чувствителен к наклону, когда ось чувствительности перпендикулярна ускорению силы тяжести, то есть параллельна поверхности Земли. А когда микроакселерометр ориентируется по оси ускорения силы тяжести, то есть вблизи показаний +1g и -1g изменение в выходном ускорении незначительно.

Результаты экспериментальных исследований представлены на рис. 38.

На рис. 39 представлена выходная характеристика образца микроакселерометра со значением масштабного коэффициента:

Км = 24,3 кГц/g –ортогонально оси чувствительности; Км = 0,38 кГц/g –сонаправленно оси чувствительности.

Так же был рассчитан коэффициент нелинейных искажений КНИ = 4%.

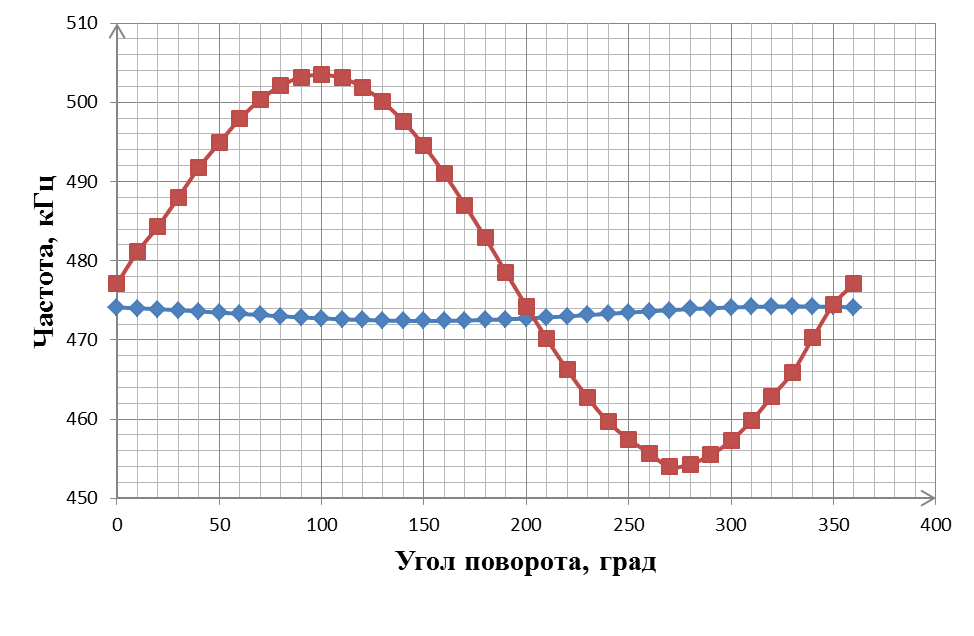
Рис. 38. Градуировка ПАВ-микроакселерометра

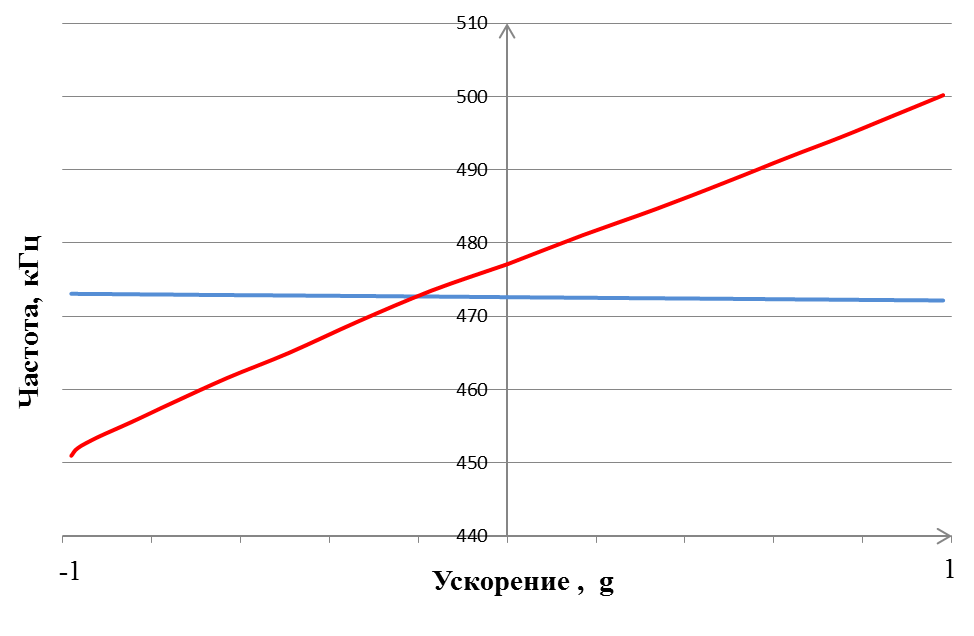
Рис. 39. Выходная характеристика ПАВ-микроакселерометра.

Заключение

По проведенной работе был выполнен анализ существующих микроакселерометров. Он показал, что при построении современных микромеханических акселерометров используются те же концепции, которые уже отобраны на их микроаналогах, но их конструктивная реализация имеет достаточно большие отличия. При проведении градуировки ММА на ПАВ в гравитационном поле Земли были получены данные, после обработки которых были построены графики градуировки и выходной характеристики в направлении по и против часовой стрелки, для каждого из них были посчитаны сдвиг нуля, масштабный коэффициент и коэффициент нелинейной выходной характеристики, который составил для направления по часовой стрелке 4,1 %, против –,8 %. При проведении экспериментальных исследований было выявлено большой время выхода на рабочий режим. Причиной тому являлось значительное тепловыделение на элементах электрической схемы. Далее была выполнена оценка чувствительности ММА к ускорениям больше ±1g при расположении инерционной массы сверху и снизу. Исследование показало, что при расположении ИМ сверху: для 1g значения составляют 22,1 кГц/g, а при 4 g –,8 кГц/g; снизу: для 1g –,2 кГц/g, 4g –,4 кГц/g. При проведении расчета чувствительности при действии гравитационных сил на чувствительный элемент ММА при действии ускорения ортогонально оси чувствительности, было выявлено, что микроакселерометр наиболее чувствителен к наклону, когда ось чувствительности перпендикулярна ускорению силы тяжести, то есть параллельна поверхности Земли. А когда микроакселерометр ориентируется по оси ускорения силы тяжести, то есть вблизи показаний +1g и -1g изменение в выходном ускорении незначительно.

Список литературы

1. Казакевич Александр. Акселерометры Analog Devices –устройство и применение. http://kit-e.ru/articles/sensor/2007_5_46.php
2. Д.П. Лукьянов, В.Я. Распопов, Ю.В. Филатов. Микромеханические навигационные приборы. Учеб. Пособие / СПбГЭТУ «ЛЭТИ». СПб., 2008, стр. 48
3. Д.П. Лукьянов. Микромеханические навигационные приборы. Учеб. Пособие / СПбГЭТУ «ЛЭТИ». СПб., 2005
4. Моделирование чувствительных элементов ММА и ММГ на ПАВ в программе ANSYS. Д.П. Лукьянов, С.Ю. Шевченко, А.С. Кукаев, Е.П. Филиппова.
5. Разработка и оптимизация схемы построения микроакселерометра на поверхностных акустических волнах (Часть 1). Д.П. Лукьянов, М.М. Шевелько, С.Ю. Шевченко и др. // Гироскопия и навигация. –. - №2(49).
6. Малов В.В. Пьезорезонансные датчики. –М.: Энергоиздат, 1989.
7. Д.П. Лукьянов, С. Ю. Шевченко, А.С. Кукаев, Д.В. Сафронов, Е.П. Филиппова. Моделирование твердотельных чувствительных элементов в программе ANSYS на примере ММА// Навигация и управление движением: Материалы докладов XIV конференции молодых ученых «Навигация и управление движением»/ под общ. ред. Академика РАН В.Г. Пешехонова. –СПб.: ГНЦ РФ ОАО «Концерн ЦНИИ Электроприбор», 2012 с.420–;
8. Конспект лекций «Современная элементная база систем управления ЛА». 6.2 Устройство и функционирование микромеханических гироскопов и акселерометров. http://lib.rushkolnik.ru/text/25071/index-1.html?page=10

25

Исследование микромеханического акселерометра на поверхностных акустических волнах