Классификация движений первого и второго родов. Движения пространства

Лекция 12. Классификация движений первого и второго родов. Движения пространства.

Литература. [1] §§ 43, 68 - 70 .

Рассмотрим классификацию движений первого рода. Справедлива следующая теорема.

Теорема 1 (теорема Шаля). Любое движение первого рода является либо тождественным преобразованием, либо параллельным переносом, либо вращением.

Доказательство. Обозначим рассматриваемое движение первого рода через g. Его аналитические выражения имеют вид (4.5), при условии, что = 1:

(71)

Как было ранее объяснено, точка M(x;y) в том и только в том случае является инвариантной точкой движения g, когда её координаты удовлетворяют системе уравнений

(2)

Возможны следующие случаи:

1) движение g имеет по крайней мере две неподвижные точки;

2) g обладает ровно одной такой точкой;

3) этих точек у движения нет.

Рассмотрим первый случай, движение g имеет, по крайней мере, две инвариантные точки. Тогда, согласно лемме 2, прямая, проходящая через них целиком состоит из неподвижных точек. Выберем ортонормированный репер так, чтобы точки и принадлежали этой прямой. Так как координаты неподвижных точек и относительно репера R равны: (0;0), (1;0), то подставляя их координаты в формулы (2), получаем: a = b = sin = 0, cos = 1. Поэтому формулы (1) имеют вид:

т.е. движение является тождественным преобразованием.

Рассмотрим второй случай, когда движение обладает единственной неподвижной точкой O. Выберем ортонормированный репер так, чтобы эта точка была его началом. В этом случае x = 0, y = 0 - решения системы (2). Поэтому в формулах (1) a = b = 0. Таким образом аналитические выражения данного движения имеют вид :

т.е. совпадают с аналитическими выражениями вращения. Поэтому во втором случае движение является вращением.

Наконец перейдем к третьему случаю, когда движение g не имеет неподвижных точек. Тогда, согласно леммы 4, это движение имеет инвариантную прямую. На этот раз выберем ортонормированный репер так, чтобы точки и принадлежали инвариантной прямой. Их координаты относительно R равны: (0;0), (1;0). Пусть . Так как принадлежит прямой , то её координаты равны (c;0). Подставляя координаты и в равенства (5.2), получим: a = c, b = 0. Длины отрезков и равны между собой, точка принадлежит прямой , поэтому её координаты равны либо (c - 1; 0), либо (c + 1; 0). Предположим, что эта точка имеет координаты (c - 1; 0). Тогда из равенств (7) следует, что

Отсюда получим, что sin = 0, cos = -1, и формулы движения g имеют вид:

Легко видеть, что полученное преобразование является центральной симметрией относительно точки Q( ; 0), для которой эта точка Q - инвариантнa. Так как мы предположили, что g не имеет инвариантных точек, то координаты точки равны (c+1; 0). Еще раз подставим координаты и в (1). Получим:

Следовательно, cos = 1, sin = 0, и формулы движения g имеют вид:

Мы вывели, что в этом случае движение g - параллельный перенос на вектор . Теорема доказана.

Теорема 2. Любое движение второго рода либо имеет бесконечно много инвариантных точек, либо не имеет их вообще.

Доказательство. Рассмотрим аналитическое выражение некоторого движения второго рода. Оно имеет вид (35.5), при условии, что = -1:

(3)

Координаты его инвариантной точки совпадают с решениями системы уравнений:

(4)

Преобразуем её к виду:

Определитель полученной системы равен

В силу полученного равенства система (4) либо не имеет решений, либо имеет их бесконечно много. Теорема доказана.

Пусть движение g второго рода обладает бесконечным множеством инвариантных точек. Легко видеть, что все они принадлежат одной прямой. Действительно, если существуют три неколлинеарные неподвижные точки движения g, то из леммы 1 вытекает, что g - тождественное преобразование, т.е. не является движением второго рода. Выберем ортонормированный репер так, чтобы точки и были инвариантными относительно g: Тогда пары чисел (0; 0) и (1; 0) служат решениями системы (36.5). Подставляя их в уравнения системы, получим: a = b = 0, cos = 1, sin = 0. Поэтому формулы g имеют следующий вид:

Данное движение, как следует из соотношений (5), - осевая симметрия относительно прямой , т.е. прямой, состоящей из инвариантных точек.

Пусть дано движение g второго рода, которое не имеет инвариантных точек. Тогда, согласно лемме 4, оно имеет инвариантную прямую. Обозначим её через l. Выберем ортонормированный репер так, чтобы точки и принадлежали l. Тогда образы этих точек также принадлежат l. Координаты точек и относительно этого репера равны: , a x = 0 является уравнением прямой l относительно R. Поэтому координаты имеют вид: (c; 0). Заменим в (36.4) x' на c, y' на 0, a вместо x и у подставим координаты точки . Получим:

a = c, b = 0 (5)

Так как =1, a точка лежит на прямой l, то её координаты равны либо: (c - 1; 0), либо (c + 1; 0). В первом случае подставим координаты точек и в соотношения (36.4) и осуществим замену по формулам (36.6). Будем иметь: cos = -1, sin = 0. Тогда аналитические выражения движения g приобретут вид:

Легко видеть, что в этом случае движение g имеет неподвижную точку, например , и вообще g является осевой симметрией с осью m: . Так как мы предполагали, что g не имеет инвариантных точек, то координаты точки равны: . Заменим в (36.4) x и у на 1 и 0, x' и y' на c+1 и 0, a a и b на с и 0, получим: cos = 1, sin = 0. Аналитическое выражение движения g имеет вид:

(6)

Нетрудно заметить, что в этом случае движение представляет собой произведение , где - осевая симметрия с осью l:

a, - параллельный перенос на вектор {c; 0}, параллельный прямой l:

Такое преобразование носит названия скользящей симметрии, прямая l - оси скользящей симметрии, а вектор - вектора скользящей симметрии.

Нами доказана теорема о классификации движений второго рода.

Теорема 3. Любое движение второго рода является либо симметрией, либо скользящей симметрией.

В заключение параграфа отметим еще одно интересное свойство осевой симметрии. Выше говорилось о том, что произведение двух движений второго рода является движением первого рода. Пусть даны две осевые симметрии и с осями l и m. Поэтому представляет собой движение первого рода и, согласно теореме Шаля, совпадает либо с тождественным преобразованием, либо с параллельным переносом, либо с вращением.

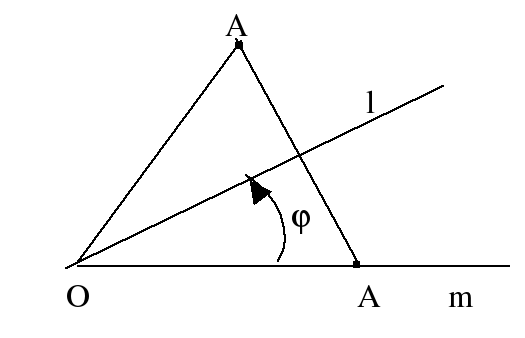
Пусть оси m и l данных осевых симметрий совпадают. Легко видеть, что в этом случае является тождественным преобразованием. Предположим, что оси l и m пересекаются в некоторой точке O. Тогда она - единственная неподвижная точка произведения . Отсюда, совпадает с вращением вокруг этой точки. Возьмем некоторую точку A, отличную от О на прямой m (рис 158, a). Тогда её образ при произведении совпадает A' = (A). Если обозначить ориентированный угол между прямыми m и l через , то AOA' = 2. Таким образом, произведение совпадает с вращением вокруг точки О на угол 2.

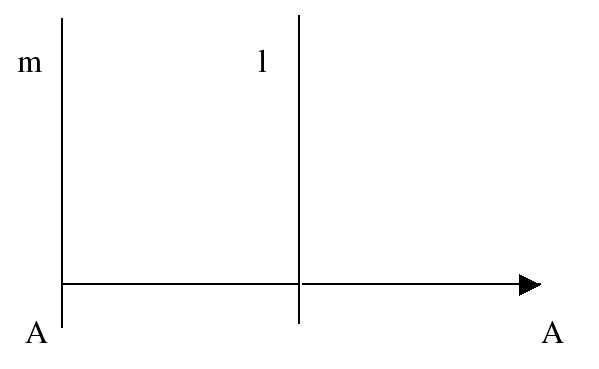
Пусть оси l и m параллельны друг другу (рис. 158, б). Легко видеть, что в этом случае произведение не имеет неподвижных точек. Поэтому оно совпадает с параллельным переносом. Нетрудно найти его вектор. Для этого достаточно выбрать точку A на прямой m и построить точку A' = (A) = (A). Вектор служит искомым.

Любое движение второго рода совпадает с произведением осевой симметрии на движение первого рода. И так, мы доказали следующую теорему:

Теорема 4. Любое движение первого рода является произведением двух осевых симметрий: а движение второго рода - либо осевой симметрией: либо произведением трех осевых симметрий.

Определение движения трехмерного пространства дословно совпадает с определением этого преобразования в случае плоскости : под движением пространства понимается такое его преобразование, при котором сохраняется расстояние между точками.

Свойства движений трехмерного пространства во многом аналогичны его свойствам в случае плоскости: при движении пространства коллинеарные точки преобразуются в коллинеарные, а точки, не лежащие на одной прямой, - в точки, которые одной прямой не принадлежат; сохраняется простое отношение точек; прямая преобразуется в прямую, отрезок - в отрезок, луч - в луч, угол - в равный ему угол; множество движений пространства образует группу преобразований. Доказательства этих утверждений дословно совпадает с доказательствами соответствуюших свойств , приведенных в § 33.

Рассмотрим те свойства движений пространства, которые не имеют соответствующих аналогов в случае плоскости.

Свойство 1. При движении пространства плоскость преобразуется в плоскость.

Доказательство. Пусть d - произвольное движение пространства, - некоторая плоскость. Выберем три неколлинеарные точки A, B и C, принадлежащие этой плоскости. Пусть A' = d(A), B' = d(B), C' = d(C). Точки A’, B’ и C' также не лежат на одной прямой Поэтому существует единственная плоскость ‘, которая содержит эти точки. Докажем, что ' = d(). Рассмотрим произвольную точку X плоскости . Выберем такую прямую l, проходящую через X, которая пересекает прямые AB и AC. Обозначим точки пересечения этих прямых соответственно через S и T (рис 164). Пусть S' = d(S), T' = d(T), X' = = d(X), l' = d(l). При движении прямые преобразуются в прямые. Поэтому точки S' и T' являются точками пересечения прямой l' соответственно с прямыми A’B’ и A’C’. Отсюда следует, что прямая l' принадлежит плоскости ‘. Так как X’ l’, то точка X’ принадлежит плоскости ‘. Мы показали, что d() ‘.

Докажем, что прообраз любой точки X’ плоскости ‘ лежит в . Для этого проведем через X’ прямую, которая пересекает A’B’ и AC’ соответственно в точках S’ и T’. Их прообразы S = (S') и T = (T') принадлежат прямым AB и АС. Поэтому прямая ST лежит в плоскости . Но X = (X') - точка прямой ST, поэтому она также принадлежит плоскости . Утверждение доказано.

Свойство 2. При движении пространства полуплоскость преобразуется в полуплоскость, двугранный угол в равный ему двугранный угол.

Свойство 3. При движении пространства скрещивающиеся прямые преобразуются в скрещивающие прямые, их общий перпендикуляр переходит в общий перпендикуляр образов и при этом сохраняется расстояние между ними.

Доказательство свойств 2 и 3 проведите самостоятельно.

Под репером пространства понимается упорядоченная четверка его точек , не лежащих в одной плоскости. Отсюда следует, что ни какие три из этих точек не принадлежат одной прямой. Также как и в случае плоскости, с репером пространства связывается система координат , где . Репер называется ортонормированным, если соответствующая ему система координат является прямоугольной декартовой. Под координатами точки относительно репера R, как и в случае плоскости, понимаются её координаты относительно соответствующей системы координат.

Теорема 1. Существует единственное движение пространства, переводяшее один ортонормированный репер в другой.

Доказательство теоремы опускаем, так как оно полностью аналогично доказательству теоремы 1 § 34. Отсюда также следует, что движение в том и только в том случае является тождественным, когда оно ортонормированный репер переводит в себя.

Справедливо также утверждение, аналогичное теореме 1 § 35: если даны два репера и пространства, ' и ' - их образы при некотором движении, то ориентации реперов и ' совпадают или различны в том и только в том случае, когда совпадают или различны ориентации реперов и ’. В силу этого утверждения движения пространства, как и в случае плоскости, подразделяются на движения первого и второго рода: оно называется движением первого рода, если оно не меняет ориентации реперов, движение имеет второй род, если ориентации реперов меняются.

Рассмотрим примеры движений пространства. Как и в случае плоскости, в пространстве определяется преобразование параллельного переноса. Пусть дан вектор . Под параллельным переносом пространства на вектор понимается такое преобразование, которое каждой точке M ставит в соответствие точку М’, удовлетворяющую условию . Очевидно, что в пространстве справедливы все свойства параллельного переноса, доказанные в § 33 для случая плоскости .

Пусть в пространстве даны ось l и некоторый угол , удовлетворяющий условию . Обозначим через орт оси l, т.е. единичный вектор, сонаправленный с осью. Рассмотрим произвольную точку M пространства. Пусть - плоскость, проходящая через M и перпендикулярная l, a О - точка пересечения плоскости и оси l (рис. 165). Ориентируем таким образом, чтобы её базис был правым в том и только в том случае, когда базис пространства является правым. Точке M поставим в соответствие такую точку M' плоскости , которая является образом M при вращении этой плоскости вокруг точки О на ориентированный угол . Такое преобразование пространства будем называть вращением вокруг оси. Если = , то точки M и M' центрально симметричны в плоскости относительно точки O. В этом случае преобразование называется отражением относительно оси. Произведение вращения вокруг оси на ненулевой вектор, параллельный оси вращения, называется винтовым движением.

Параллельный перенос, вращение вокруг оси и винтовое движение являются движениями первого рода пространства.

Пусть в пространстве дана точка O. Каждой точке M пространства поставим в соответствие такую точку М’, для которой О служит серединой отрезка ММ’. Такое преобразование пространства называется центральной симметрией относительно точки O. Если начало системы координат совпадает с центром O, то формулы этого преобразования имеют вид:

(38.1)

Покажем, что центральная симметрия представляет собой движение второго рода пространства. Выберем репер , пространства таким образом, чтобы его первая базисная точка совпадала с центром симметрии. Тогда, согласно cистеме (38.1), этот репер преобразуется в репер , для которого . Матрица перехода от R к R' имеет вид

(RR') =

Её определитель равен -1. Oриентации реперов R и R' различны и центральная симметрия - преобразование второго рода пространства.

Определим в пространстве преобразование симметрии относительно плоскости. Пусть дана плоскость . Каждой точке N плоскости поставим в соответствие ту же точку N. Если точка M не принадлежит этой плоскости, то поставим ей в соответствие такую точку М’, для которой прямая ММ’ перпендикулярна плоскости , a точка P их пересечения служит серединой отрезка ММ’ (рис. 166).

Пусть в пространстве выбрана некоторая ось l и плоскость , которая ей перпендикулярна. Произведение вращения вокруг оси l на симметрию относительно плоскости p называется поворотным отражением. Предположим, что в пространстве даны плоскость и некоторый ненулевой вектор , который ей параллелен. Произведение параллельного переноса на вектор на симметрию относительно плоскости называется скользящей симметрией. Симметрия относительно плоскости, поворотное и скользящее отражения - движения второго рода.

Как и в случае плоскости, классификация движений пространства проводится по числу их инвариантных точек и прямых. Справедлива следующая теорема, которую мы приводим без доказательства.

Теорема 2. Любое движение пространства принадлежит к одному из следующих типов:

- Движения первого рода: тождественное преобразование, параллельный перенос на ненулевой вектор, вращение относительно оси и винтовое движение.

- Движения второго рода: симметрия относительно точки, симметрия относительно плоскости, поворотное отражение с углом , где 0, , и скользящее отражение.

Применение видов движений при решении задач на построение является весьма многообразным. Можно сказать, что суть рассматриваемого метода состоит в отыскании при анализе задачи подходящего движения данных фигур или их элементов, позволяющего построить вспомогательную фигуру, в частности точку, определяющую искомую фигуру. Выполнение построения предполагает умение строить образы точек, прямых и окружностей при различных движениях плоскости, что не вызывает принципиальных затруднений

Классификация движений первого и второго родов. Движения пространства