Отображения и преобразования множеств. Аналитическое выражение преобразований, группа преобразований. Движения плоскости. Простейшие виды движений

Лекция 9. Отображения и преобразования множеств. Аналитическое выражение преобразований, группа преобразований. Движения плоскости. Простейшие виды движений

Литература. [1] § 39, 40.

Пусть дано отображение . Если для любого элемента y из существует только один прообраз, то отображение называется инъективным или однозначным. В этом случае нельзя найти два элемента и множества X, для которых . Если при отображении f выполнено условие: , т.е. для любого элемента из Y существует по крайней мере один прообраз, то отображение называется сюръективным или отображением X на Y. Отображение, которое одновременно является сюръективным и инъективным, носит название биективного или взаимно однозначного отображения. Таким образом, отображение тогда и только тогда является биективным, когда для любого элемента y из множества Y существует один и только один элемент x из X, для которого .

Пусть взаимно однозначное отображение множества X на множество Y. Поставим в соответствие каждому элементу y из Y его прообраз x из множества X. Мы построили отображение , которое носит название обратного к отображению . Оно обычно обозначается через . Легко показать, что также биективное отображение. Действительно, в силу того, что взаимно однозначное отображение, для любого элемента y из Y существует один и только один прообраз x в множестве X. Таким образом, каждому элементу y из Y ставится в соответствие один и только один элемент из X.

Определение 1. Взаимно однозначное отображение множества X на себя называется преобразованием этого множества.

Если дана некоторая плоскость, то её отображение в себя можно задать в координатной форме. Выберем на плоскости некоторую аффинную систему координат. Рассмотрим отображение . Будем считать, что точке ставится в соответствие точка . Координаты точки зависят от , координат точки :

(1)

Обратно, если заданы функции (1), то можно считать что они определяют некоторое отображение плоскости в себя: каждой точке ставится в соответствие точка . Соотношения (1) называются аналитическим выражением или формулами отображения f.

Пример 1. Отображение f задано своими аналитическим выражением Выяснить, является ли оно преобразованием плоскости.

Решение. Проверим условия инъективности и сюръективности. Пусть и - точки, удовлетворяющие условию . Тогда: Отсюда: Мы получили систему уравнений относительно и . Легко видеть, она совместна и имеет единственное решение . Таким образом, из условия следует, что точки и совпадают. Отображение f является инъективным.

Пусть  произвольная точка плоскости. Для того чтобы существовала такая точка A, для которой , достаточно, чтобы её координаты удовлетворяли системе уравнений: Так как определитель этой системы отличен от нуля, то она всегда имеет единственное решение. Нетрудно выразить x и y через x' и y'. Для этого сложим уравнения системы и вычтем из первого удвоенное второе. После преобразований получим: Сюръективность отображения f доказана. Таким образом, f  преобразование плоскости.

Пример 2. Дано аналитическое представление преобразования f плоскости:

Найти формулы обратного преобразования.

Решение. Отображение каждой точке плоскости ставит в соответствие точку , для которой . Обозначим координаты точек и через x, y и x', y'. Из данного аналитического представления следует: Выразим отсюда x', y' через x, y: , . Таким образом, формулы обратного преобразования имеют вид:

Рассмотрим примеры необходимых нам преобразований плоскости и выведем их аналитические выражения.

Определение 2. Пусть дан вектор . Отображение плоскости на себя, которое каждой точке M ставит в соответствие такую точку M', для которой называется параллельным переносом плоскости на вектор .

Легко видеть, параллельный перенос является преобразованием плоскости, его будем обозначать через . Найдем аналитическое выражение параллельного переноса. Пусть в выбранной системе координаты вектор равны . Предположим, что точка M имеет координаты x и y, a её образ  x' и y'. Так как , то . Отсюда получим формулы параллельного переноса:

(2)

Рассмотрим еще одно преобразование  вращение плоскости.

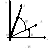
Определение 3. Пусть на ориентированной плоскости даны точка O и ориентированный угол . Преобразование, которое точке O ставит в соответствие ту же точку O, а любой точке A, отличной от O, - точку A', удовлетворяющую условиям: . называется вращением плоскости с центром в точке O на угол .

Преобразование вращения будем обозначать через . Найдем его аналитическое выражение, при условии, что на плоскости дана прямоугольная декартова система координат, а центр вращения совпадает с ее началом.

Решение. Пусть точка A имеет координаты x и y, а её образ - x' и y'. Обозначим через ориентированный угол между положительным направлением оси абсцисс и вектором (рис. 125). Тогда ориентированный угол между векторами и равен . Как было показано, , и , . Так как OA=OA', то

==,==

Таким образом:

(3)

Соотношения (3) представляют собой аналитическое выражение вращения.

При формулы вращения имеют вид: В этом случае преобразование представляет собой центральную симметрию относительно центра вращения.

Определение 4. Пусть дана прямая l. Отображение, которое каждой точке прямой l ставит в соответствие ту же точку, a точке A, не принадлежащей l, - точку A', удовлетворяющую условиям: прямая AA' перпендикулярна l и середина отрезка AA' принадлежит l, называется осевой симметрией плоскости с осью l.

Осевую симметрию будем обозначать через . Докажите самостоятельно, что осевая симметрия – преобразование плоскости. Пусть на плоскости выбрана прямоугольная декартовая система координат. Найдем аналитическое выражение осевой симметрии, при условии, что ее ось совпадает с осью абсцисс. Обозначим координаты точки A через x и y, а её образа A' при указанной симметрии  x' и y' (рис. 126). Тогда вектор параллелен оси ординат, a середина M отрезка AA' лежит на оси абсцисс. Координаты вектора и точки M соответственно равны , . Используя условие параллельности вектора оси Оу, получим: или . Так как точка M лежит на оси Ох, то . Таким образом:

(4)

Формулы (4) являются искомым аналитическим выражением осевой симметрии.

Определение 5. Пусть f и g – два преобразования множества Х. Под произведением преобразования f на преобразование g будем понимать отображение, определяемое формулой , где х – произвольный элемент множества Х.

Покажем, что произведение преобразований также является преобразованием множества Х. Пусть . Так как f и g  биективные отображения множества X на себя, то из следует и . Поэтому h инъективное отображение. Докажем его сюръективность. Пусть y - произвольный элемент из X. Тогда существует такой элемент z, что . Аналогично, существует такой элемент x из множества X, для которого . Отсюда вытекает, что . Таким образом, h  сюръективное отображение. Биективность h доказана.

Пример 3. Найти формулы произведения , если даны аналитические выражения преобразований f и g:

Решение. Возьмем произвольную точку . Пусть , тогда координаты M' равны . Обозначим через M" образ точки M' при преобразовании g: . Используя формулы преобразования g, найдем координаты этой точки: , или . Таким образом, аналитическое выражение преобразования имеет вид:

Замечание. Если мы определим формулы произведения , то получим: (проведите вычисления самостоятельно). Отсюда видно, что произведение преобразований, вообще говоря, не обладает свойством коммутативности.

Определение 6. Преобразование, которое каждому элементу множества X ставит в соответствие тот же самый элемент, называется тождественным.

Тождественное преобразование обычно обозначается через e. Легко видеть, что аналитическое выражение тождественного преобразования плоскости имеет вид: Тождественное преобразование является нейтральным элементом относительно операции произведения преобразований, что означает, что для любого преобразования :. Действительно, возьмем произвольный элемент x множества X: .

Выберем произвольное преобразование и найдем произведение . Пусть y произвольный элемент множества X. Согласно определению обратного преобразования, элемент удовлетворяет условию: . Поэтому . Отсюда следует, что . Возьмем произвольный элемент х множества Х. Пусть , тогда . Таким образом, . Или: . Мы показали, что преобразование - обратное к преобразованию относительно операции произведения преобразований. И так, операция произведения преобразований обладает свойством обратимости. Она же, как отмечалось выше, не удовлетворяет свойству коммутативности. Докажем ее ассоциативность.

Теорема 1. Для любых трех преобразований f, g и h множества X справедливо равенство: .

Доказательство. Пусть x произвольный элемент множества X. Тогда из определения произведения преобразований получим: С другой стороны, Таким образом, для любого элемент x справедливо равенство: . Теорема доказана.

Из курса алгебры известно, что множество G называется группой, если на нем определена ассоциативная и обратимая алгебраическая операция. Если эта операция коммутативна, то G называется абелевой группой. Пусть F совокупность всех преобразований множества X. Произведение преобразований является ассоциативной и обратимой алгебраической операцией на F. Поэтому F  группа относительно операции произведения преобразований. Она, вообще говоря, не является абелевой.

Определение 7. Любая подгруппа группы F называется группой преобразований множества X.

Пусть G - подмножество F. В силу теоремы 1, G тогда и только тогда группа преобразований, когда операция произведения преобразований алгебраически замкнута и обратима на G. Поэтому G группа преобразований в том и только в том случае, когда для любых двух элементов f и g из G их произведение принадлежит G, и для любого элемента f этому же множеству принадлежит и обратное преобразование .

Пример 4. Доказать, что множество, состоящее из четырех преобразований f, g, h и e образуют группу преобразований плоскости.

f: g: h: e:

Решение. Составим таблицу произведений элементов из G:

I \ II	e	f	g	h
e	e	f	g	h
f	f	e	h	g
g	g	h	e	f
h	h	g	f	e

В таблице на пересечении соответствующей строки и столбца помещен результат произведения , те произведение элемента строки, умноженной слева на элемент столбца. Проверим, например, что. Пусть точка M имеет координаты x и y, . Точка M' имеет координаты . Поэтому координаты точки равны . Отсюда следует, что . Результаты остальных произведений проверьте самостоятельно. Из таблицы следует, операция произведения преобразований алгебраически замкнута на G. Легко видеть, что e  тождественное преобразование в G. Каждый элемент из G имеет обратный, причем он совпадает с самим элементом: . Нами проверено, что G  группа преобразований.

Определение 1. Преобразование плоскости называется движением, если расстояние между образами любых двух точек совпадает с расстоянием между самими точками.

Таким образом, f движение плоскости в том и только в том случае, когда для любых двух её точек A и В выполнено равенство: .

Покажем, что параллельный перенос, вращение и осевая симметрия, введенные нами в предыдущем параграфе,  движения плоскости.

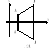
Рассмотрим параллельный перенос плоскости на вектор . Пусть A и В две произвольные точки, ,  их образы при рассматриваемом параллельном переносе. Следует доказать, что . Из определения параллельного переноса (см. § 28) получим: . Представим вектор в виде: (рис. 127). Отсюда следует, что . Так как векторы равны, то их длины совпадают. Параллельный перенос является движением.

Рассмотрим осевую симметрию с осью l. Пусть A и В - две произвольные точки, - их образы при данной осевой симметрии. Докажем, что . Выберем прямоугольную декартову систему координат так, чтобы ось абсцисс содержала прямую l (рис. 128). Если в этой системе точки А и В имеют координаты: , то из формулы осевой симметрии (см § 28) следует, что координаты точек A, и B равны: ). Найдем расстояния между этими точками: . Осевая симметрия – движение плоскости.

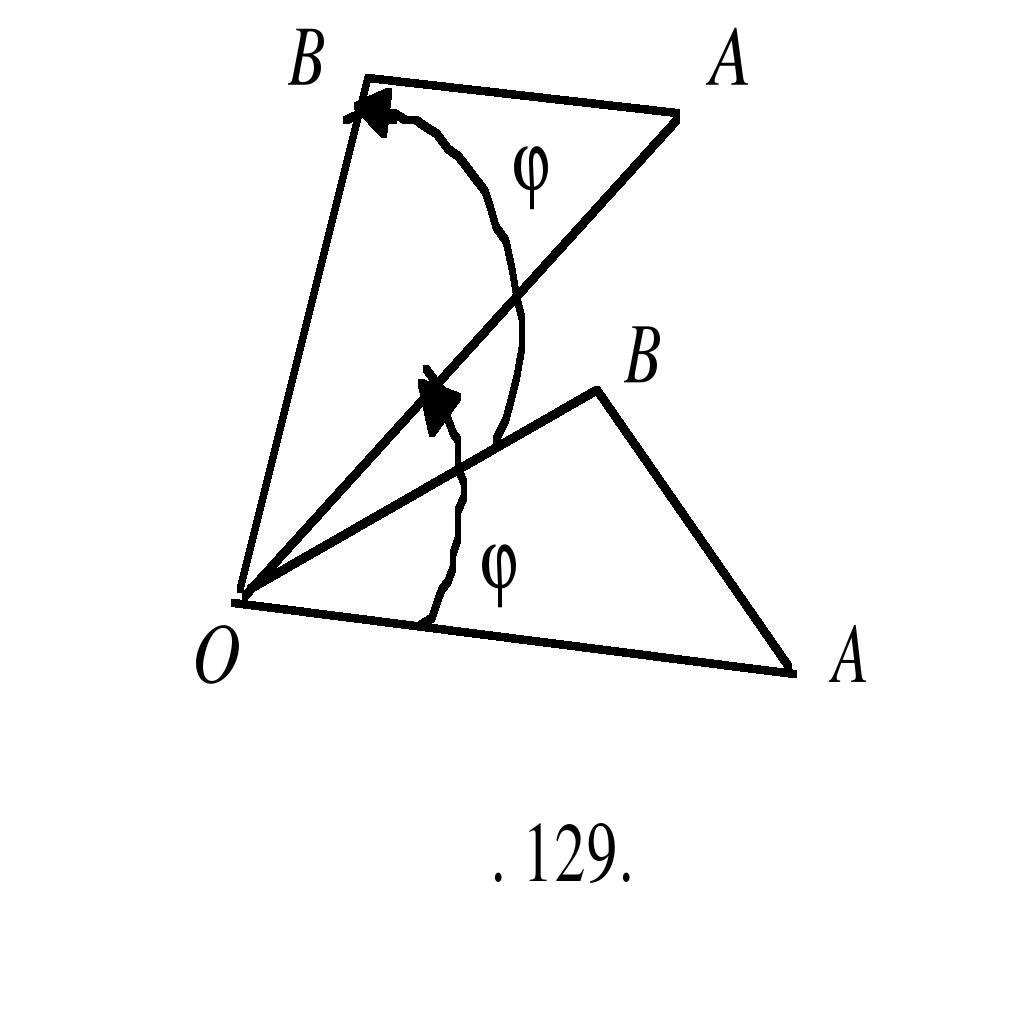
Наконец, рассмотрим вращение плоскости и покажем, что оно также является движением плоскости. Пусть A и B - две произвольные точки,  их образы при вращении вокруг точки О на ориентированный угол (рис. 129). Воспользуемся аналитическими выражением вращения (см. § 28). Выберем прямоугольную декартовую систему координат так, чтобы её начало совпадало с центром О вращения. Пусть точки A, B, A', B' в этой системе имеют координаты: . Из формул вращения следует: Вычислим расстояние между точками A' и B':

Таким образом, при вращении сохраняется расстояние между точками. Утверждение доказано.

Отображения и преобразования множеств. Аналитическое выражение преобразований, группа преобразований. Движения плоскости. Простейшие виды движений