Классификация подобий. Подобия пространства. Применение свойств подобия к решению задач элементарной геометрии

Лекция 15. Классификация подобий. Подобия пространства. Применение свойств подобия к решению задач элементарной геометрии

Литература. [1] § 46, 47, 51.

Определим аналитические выражения подобия. Представим данное подобие p в виде произведения движения d на гомотетию H, причем в качестве центра гомотетии примем начало прямоугольной декартовой системы координат. Тогда аналитические выражения движения и гомотетии, как следует из результатов настоящего параграфа и параграфа 29, имеют вид: Для нахождения формул произведения следует подставить аналитические выражения гомотетии H в формулы движения d. Получим

(1)

В случае, когда = 1, подобие называется подобием первого рода. Если = -1, то подобие носит название подобия второго рода. Если , то подобие является движением. При этом соотношения (1) совпадают с формулами движения.

Рассмотрим ортонормированный репер O(0: 0), (1: 0), (0: 1), определяющий прямоугольную декартовую систему координат. При подобии, заданном формулами (1), репер R преобразуется в репер координаты базисных точек которого равны: . Легко проверить, что при подобии первого рода ориентации реперов R и R' совпадают, a при подобии второго рода их ориентации различны.

Проведем классификацию подобий. Докажем теорему о числе инвариантных точек подобия.

Теорема 1. Любое подобие, отличное от движения, имеет одну и только одну инвариантную точку.

Доказательство. Рассмотрим подобие p плоскости, отличное от движения. Тогда его коэффициент k не совпадает с единицей. Аналитическое выражение подобия имеет вид (32.3). Точка M тогда и только тогда является инвариантной точкой подобия p, когда её координаты x и у удовлетворяют системе уравнений: Преобразуем её к виду:

(2)

Система линейных уравнений тогда и только тогда имеет единственное решение, когда ее определитель отличен от нуля. В случае подобия первого рода = 1, определитель системы (2) равен: Поэтому = 0 в том и только в том случае, когда Из второго равенства следует, что . Тогда из первого получим: k = 1 или k = -1. Так как коэффициент подобия всегда положителен, то . Но, с другой стороны, данное подобие отлично от движения, поэтому . Таким образом, 0. Для подобий первого рода утверждение доказано.

Рассмотрим теперь подобие второго рода. В этом случае = -1. Определитель системы (2) имеет вид: По условию подобие не является движением, поэтому . Отсюда следует, что , и система (2) имеет единственное решение. Теорема доказана полностью.

Следствие. Если подобие имеет хотя бы две неподвижные точки или не имеет их вообще, то оно является движением.

Инвариантная точка подобия, отличного от движения, называется его центром.

Проведем классификацию подобий. Пусть p подобие первого рода, отличное от движения. Согласно доказанной теореме, оно имеет единственную неподвижную точку O. Представим подобие в виде произведения гомотетии H на движение . В соответствии с выводом, полученном из доказательства теоремы 1, можно считать, что центр О подобия совпадет с центром гомотетии. Легко видеть, что в этом случае О  также неподвижная точка движения d. Так как p - подобие первого рода, то d - также движение первого рода. Поэтому из теоремы Шаля следует что оно является либо параллельным переносом, либо тождественным преобразованием, либо вращением. Можно считать, что тождественное преобразование представляет собой вращение на нулевой угол. Параллельный перенос не имеет неподвижных точек, поэтому d представляет собой вращение плоскости вокруг центра подобия, точки O. Таким образом, подобие первого рода, отличное от движения, является произведением гомотетии на вращение, причем центр подобия служит и центром гомотетии, и центром вращения. Такое подобие называется центрально-подобным вращением.

Пусть p  подобие второго рода, отличное от движения. Обозначим через О его центр подобия и представим p в виде произведения гомотетии H на движение d: . Как отмечалось выше, можно считать, что О - центр гомотетии H. Кроме того, О - единственная неподвижная точка движения d. Из классификации движений второго рода следует, что d совпадает либо с осевой, либо со скользящей симметрией. Но скользящая симметрия не имеет инвариантных точек. Поэтому в данном случае движение d представляет собой осевую симметрию, и, при этом, центр О гомотетии H принадлежит оси симметрии d. Таким образом, рассматриваемое подобие представляет собой произведение гомотетии на осевую симметрию, центр подобия совпадает с центром гомотетии и лежит на оси симметрии. Такого рода подобие называются центрально-подобной симметрией.

Мы провели классификацию подобий первого и второго рода, отличных от движений. Движения, в свою очередь, являются частными случаями подобий. Их классификацию была уже проведена. Итак, доказано следующее утверждение.

Теорема 2. Любое подобие первого рода является либо тождественным преобразованием, либо параллельным переносом, либо вращением, либо центрально-подобным вращением, а подобие второго рода - либо скользящей, либо осевой, либо центрально-подобной симметрией.

Докажем групповое свойство подобия.

Теорема 3. Подобия плоскости образуют группу преобразований.

Доказательство. Нам достаточно проверить, что как произведение подобий, так и обратное к подобию преобразование также являются подобиями.

Пусть даны подобия p1 и p2, коэффициенты которых равны kи k. Рассмотрим две произвольные точки A и B. Пусть , , . Так как p и p - подобия, то

A"B" = p (A') p (B') = kA'B' = k p (A) p (B)= kkAB.

Таким образом, произведение представляет собой подобие с коэффициентом kk.

Рассмотрим некоторое подобие p с коэффициентом k и обозначим через A и В прообразы двух произвольных точек A и B: . Тогда . Так как p - подобие, то , следовательно, . Отсюда вытекает, что обратное преобразование p-1 также является подобием с коэффициентом . Теорема доказана.

Как было показано в § 28, движения плоскости образуют группу преобразований. С другой стороны, движения плоскости - подобия с коэффициентом, равным единице. Поэтому движения образуют подгруппу в группе подобий.

Еще одними примером подгруппы в группе подобий является множество гомотетий с фиксированным центром. Согласно свойству 2 настоящего параграфа это множество образует группу преобразований плоскости, т.е. подгруппу в группе подобий. Нетрудно показать, что тождественные преобразования, вращения и центрально-подобные вращения составляют подгруппу в группе подобий, a подобия второго рода ее не образуют (проверьте самостоятельно).

Введем следующее определение.

Определение 1. Две фигуры F и F' называются подобными, если существует такое преобразование подобия p, при котором F' = p (F).

Как мы видим, подобие фигур аналогично понятию их геометрического равенства, которое мы рассматривали в параграфе 28. В школьном курсе геометрии фундаментальное значение имеют свойства подобных треугольников. Докажем следующую теорему.

Теорема 1. Два треугольника АВС и А’В’С’ подобны между собой в том и только в том случае, когда

(3)

Доказательство. Пусть существует преобразование подобия p, при котором , , . Из свойств подобий следует, что углы преобразуются в равные углы, а отношение соответствующих отрезков равно коэффициенту подобия. Поэтому для подобных треугольников справедливы соотношения (3).

Обратно. Пусть даны треугольники АВС и АВС, для которых выполнены равенства (3). Рассмотрим гомотетию с центром в точке A и коэффициентом . Обозначим через B" и C" образы вершин В и С при этой гомотетии: (рис. 145). Тогда AB":AB = AC":AC = B"C":BC = k. Из равенств (3) следует, что AB"=A'B', AC"=A'C', B"C"=B'C'. При гомотетии сохраняются углы треугольника. Поэтому B"=B', C"=C'. Соответственные стороны и углы треугольников АВС и АВС равны между собой. Отсюда получим, что эти треугольники равны между собой. Существует движение d, переводящее один треугольник во второй: . Следовательно, подобие переводит треугольник АВС в треугольник АВС. Теорема доказана.

В школьных учебниках по определению под подобными треугольниками понимаются те из них, которые удовлетворяют условиям (3). Под подобными же многоугольниками понимаются такие, у которых соответственные стороны пропорциональны, а соответственные углы равны между собой. Можно доказать, что и в этом случае существует подобие, переводящее один многоугольник во второй.

Выясним, при каких условиях подобны две кривые второго порядка. Докажем следующую теорему.

Теорема 2. Любые две параболы подобны между собой.

Доказательство. Рассмотрим две параболы и . Тогда, как было доказано, существуют ортонормированные реперы и , в которых их уравнения имеют канонический вид: . Как следует из основного свойства движений существует движение d, которое переводит репер R в R. При этом парабола преобразуется в параболу , которая в репере Rимеет то же уравнение , что и парабола в репере R (рис. 146).

Рассмотрим гомотетию с центром в точке О и коэффициентом . Пусть . Легко видеть, что уравнение в репере Rимеет вид . Поэтому параболы и совпадают друг с другом. Таким образом, подобие переводит в . Теорема доказана.

Можно показать, что два эллипса (гиперболы) подобны друг другу в том и только в том случае, когда совпадают их эксцентриситеты.

Понятие гомотетии и подобия пространства вводится точно так же, как и в случае плоскости. Их свойства в пространстве во многом совпадают со свойствами этих преобразований на плоскости. При гомотетиях и подобиях пространства прямые преобразуются в прямые, отрезки и лучи - в отрезки и лучи, углы – в равные углы. Подобия пространства являются произведением гомотетии на движение. Они образуют группу преобразований. Доказательства этих свойств проводятся также, как и в случае плоскости. Можно показать, что при подобии пространства плоскости преобразуются в плоскости, а двугранные углы – в равные двугранные углы. Доказательства этих утверждений проводятся аналогично как и в случае движений плоскости.

Применения преобразований подобия и гомотетии при решении задач элементарной геометрии аналогичен разобранным выше способам решения этих задач с применением движения. Преобразования подобия и гомотетии можно использовать для построения образов либо данных фигур, либо их элементов для отыскания закономерностей, позволяющих решить задачу.

Пример 1. Даны две окружности и , которые касаются в точке К. Через точку К проведены две секущие, первая пересекает и , в точках А и С, а вторая в точках B и D. Доказать, что четырехугольник АВСD – трапеция.

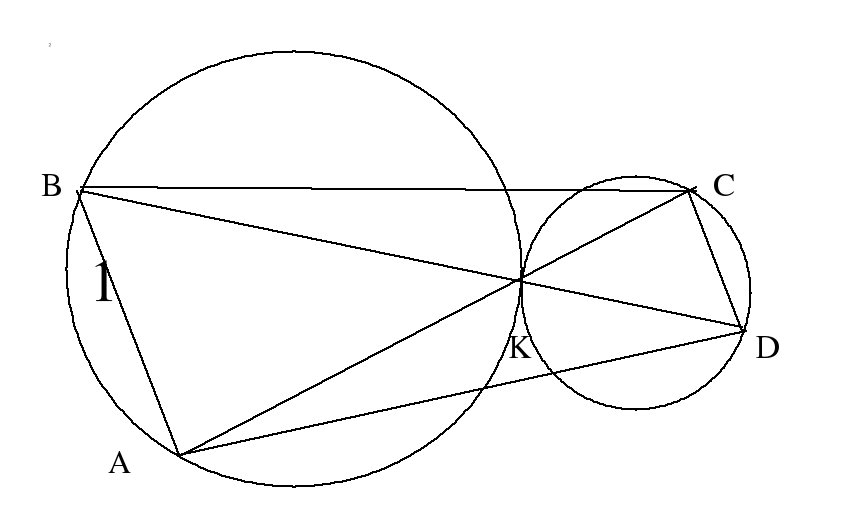
Указание. Следует рассмотреть гомотетию с центром в точке К с коэффициентом, равным отношению радиусов окружностей, взятых с обратным знаком.

Классификация подобий. Подобия пространства. Применение свойств подобия к решению задач элементарной геометрии