Аффинные преобразования и их свойства. Группа аффинных преобразований

Лекция 16. Аффинные преобразования и их свойства. Группа аффинных преобразований.

Литература. [1] § 48.

Определение 1. Преобразование плоскости называется аффинным, если оно переводит коллинеарные точки в коллинеарные и сохраняет простое отношение точек.

Таким образом, преобразование f в том и только в том случае аффинное, когда для любых трех коллинеарных точек А, В и С выполнено:

а) точки лежат на одной прямой;

б) .

Из утверждений, доказанных в предыдущих параграфах, следует, что движения и подобия плоскости  аффинные преобразования.

Рассмотрим свойства аффинных преобразований.

Свойство 1. При аффинном преобразовании точки, не лежащие на одной прямой, преобразуются в точки, не лежащие на одной прямой.

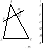
Доказательство. Предположим, что неколлинеарные точки А, В и С при аффинном преобразовании f перешли в точки , которые принадлежат одной прямой l' (рис. 155). Рассмотрим произвольную точку M плоскости. Так как A, В и С расположены в вершинах треугольника, то существует прямая, проходящая через M и пересекающая две его стороны. Пусть она пересекает сторону AB в точке P, a сторону BC в Q. Обозначим через P' и Q' образы этих точек при преобразовании . Точки А, В и P лежат на одной прямой, поэтому A, B и P также расположены на одной прямой. Так как , то . Аналогично доказывается, что точка Q также принадлежит прямой l. С другой стороны, точка M расположена на прямой РQ. Следовательно, точка лежит на прямой PQ, т.е. . Мы показали, что образ любой точки плоскости принадлежит прямой l, поэтому отображение f не является преобразованием, так как оно не сюръективно. Предположение о коллинеарности точек A, В и С привело к противоречию. Свойство доказано.

Свойство 2. При аффинном преобразовании аффинный репер отображается в аффинный репер.

Доказательство этого предложения непосредственно вытекает из свойства 1.

Свойство 3. При аффинном преобразовании образом прямой линии является прямая линия.

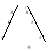
Доказательство. Пусть дано аффинное преобразование f. Рассмотрим произвольную прямую l, A и В  её две точки. Обозначим через A и B их образы при данном преобразовании: , a через l  прямую АВ. Докажем, что . Рассмотрим произвольную точку С прямой l. Как следует из определения аффинного преобразования, точка принадлежит l. Поэтому . Проверим, что прообраз любой точки прямой l лежит на l. Выберем на l произвольную точку M (рис. 156). Пусть  простое отношение . На прямой l существует единственная точка M, для которой . В силу свойств аффинного преобразования, образ лежит на прямой AB, которая совпадает с l, и . Поэтому . Утверждение доказано.

Свойство 4. При аффинном преобразовании параллельные прямые преобразуются в параллельные прямые.

Доказательство. Рассмотрим параллельные прямые m и n. Обозначим через m и n их образы при аффинном преобразовании f. Предположим, что m и n пересекаются в точке Р. Тогда прообраз P этой точки принадлежит как прямой m, так и прямой n. Таким образом, m и n пересекаются в точке P, что противоречит условию. Свойство доказано.

Свойство 5. При аффинном преобразовании отрезок переходит в отрезок, луч в луч, угол в угол.

Доказательство. Пусть f - аффинное преобразование. Рассмотрим отрезок АВ. Пусть . Точка С тогда и только тогда принадлежит этому отрезку, когда . Если , то из определения аффинного преобразования следует, что C принадлежит прямой AB и .Следовательно, . Поэтому точка C лежит на отрезке AB и .

Обратно. Пусть M  точка отрезка AB, a M - её прообраз. Согласно свойству 3 точка M лежит на прямой АВ. Кроме того, . Поэтому точка M лежит на отрезке АВ. Таким образом, .

Аналогично показывается, что образом луча при аффинном преобразовании служит луч. Доказательство проведите самостоятельно. Два луча, имеющие общее начало и не лежащие на одной прямой, образуют угол. Из доказанных свойств вытекает, что угол при аффинном преобразовании переходит в угол. Свойство доказано.

Проверим групповое свойство аффинных преобразований.

Теорема 1. Множество аффинных преобразований плоскости образует группу.

Доказательство. Необходимо проверить, что произведение аффинных преобразований плоскости и обратное к аффинному преобразованию являются также аффинными преобразованиями.

Пусть f и g - аффинные преобразования, А, В и С - коллинеарные точки. Тогда точки также лежат на одной прямой. Отсюда следует, что точки  коллинеарные. Мы проверили, что произведение аффинных преобразований сохраняет коллинеарность точек. В силу того, что и f и g не меняют простого отношения точек, получим: . Отсюда следует, что преобразование сохраняет простое отношение точек.

Пусть f  произвольное аффинное преобразование, A, В и С  коллинеарные точки. Обозначим их прообразы через: , и . Предположим, что точки не лежат на одной прямой. Но . Отсюда и из свойства 1 следует, что точки A, В и С также не коллинеарные. Мы получили противоречие, которое доказывает коллинеарность точек A, Ви С. Рассмотрим их простое отношение. Из определения аффинного преобразования следует, что . Поэтому . Обратное преобразование также является аффинным. Теорема доказана.

Как ранее отмечалось, движения и подобия являются частными случаями аффинных преобразований. Очевидно следующее утверждение.

Следствие. Движения и подобия составляют подгруппы в группе аффинных преобразований.

Группа аффинных преобразований, как будет вытекать из следующего утверждения, гораздо шире группы подобий. Она содержит подгруппы, отличные от подобий.

Докажем основную теорему аффинных преобразований.

Теорема 2. Пусть даны два аффинных репера и Существует единственное аффинное преобразование, переводящее репер Rв R.

Доказательство. Установим существование такого преобразования. Пусть M - произвольная точка плоскости. Обозначим её координаты относительно репера R через x и y: . Поставим ей в соответствие точку , координаты которой относительно Rтакже равны x и y: . Очевидно, что такое соответствие задает преобразование f плоскости. Рассмотрим коллинеарные точки A, В и C, координаты которых относительно репера R равны: . Пусть . Тогда . Эти векторы в репере R имеют следующие координаты: , . Поэтому они пропорциональны с коэффициентом . Пусть . Тогда их координаты относительно репера R равны: . Тогда: . Но полученные пары чисел являются пропорциональными с тем же коэффициентом . Следовательно, .Таким образом, точки лежат на одной прямой и . Мы доказали, что f  аффинное преобразование.

Проверим единственность. Пусть существуют два аффинных преобразования gи g, удовлетворяющих условию:

(34.1)

Рассмотрим произвольную точку M плоскости и проведем через неё прямую, пересекающую прямые и соответственно в точках P и Q (рис. 157). Преобразования gи g- аффинные. В силу равенств (34.1) точки и принадлежат прямой (см. рис 157). Обозначим через . Тогда = = . Так как на прямой существует единственная точка, удовлетворяющая полученным равенствам, то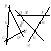

= = Р. Аналогично доказывается, что Обозначим простое отношение (PQ,M) через . Точки и лежат на прямой PQ, поэтому: = = = . Таким образом, как точка , так и точка делят отрезок PQ в одном и том же отношении . Следовательно, для произвольной точки M выполнено: =. Преобразования gи g совпадают друг с другом. Теорема доказана.

Следствие 1. Если аффинное преобразование g отображает репер в репер , то каждой точке M с координатами x и у относительно репера ставится в соответствие точка g(M) с теми же координатами относительно репера .

Действительно, при доказательстве теоремы 2 мы построили преобразование f, удовлетворяющее указанному свойству. В силу условия единственности f = g.

Следствие 2. Если аффинное преобразование f имеет три неподвижные точки, не принадлежащие одной прямой, то оно совпадает с тождественным преобразованием.

В самом деле, если A, В и С - инвариантные точки аффинного преобразования f, не лежащие на одной прямой, то они образуют некоторый репер R. Поэтому . С другой стороны, если e тождественное преобразование, то . Поэтому f = e.

Теорема 2 позволяет определить любое аффинное преобразование плоскости. Для этого достаточно задать два соответствующих друг другу аффинных репера.

Теорема 3 (основное свойство аффинных преобразований). Даны реперы Rи R, и - их образы при некотором аффинном преобразовании f. Тогда ориентации реперов и совпадают в том и только в том случае, когда совпадают ориентации R и .

Доказательство этой теоремы дословно совпадает с доказательством соответствующего утверждения параграфа 30. Поэтому мы его опускаем. Теорема 3 обосновывает корректность следующего определения.

Определение 2. Аффинное преобразование f называется аффинным преобразованием первого рода, если ориентация любого репера R совпадает с ориентацией его образа, репера R' = f(R). Оно называется аффинным преобразованием второго рода, если ориентации R и R' различны.

Выведем формулы аффинного преобразования. Пусть такое преобразование f переводит репер в репер . Известны координаты точки в репере и векторов и в базисе : . В параграфе 9 нами были получены формулы перехода от одной аффинной системы координат к другой. Если точка P имеет координаты относительно репера и относительно репера , то числа (i = 1, 2), a и b связаны между собой равенствами: При этом матрица является невырожденной, а её определитель больше нуля, в том случае, когда ориентации реперов и одинаковые и меньше нуля, если их ориентации различны. Выберем произвольную точку M плоскости и обозначим через M её образ при преобразовании . Пусть координаты точки M относительно репера равны , а её образ M' имеет в координаты: . Тогда из следствия теоремы 2 вытекает, что координаты точки M относительно репера равны: . Применим формулы перехода от одной аффинной системы координат к другой к точке М. При этом в указанных формулах uи u следует заменить на x и y, а v и v  на x и y:

(34.2)

где

= 0. (34.3)

Здесь > 0, если f - аффинное преобразование первого рода и < 0, если f имеет второй род. Соотношения (34.2) служат аналитическими выражениями аффинного преобразования. Легко видеть, что аналитические выражения движений и подобий представляют собой частные случаи формул (34.2).

Аффинные преобразования и их свойства. Группа аффинных преобразований