Задание на курсовую работу Анализ линейных электрических цепей в установившихся режимах
КУРСОВАЯ РАБОТА
по дисциплине «Теоретические основы электротехники»
АНАЛИЗ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
В установившихся РЕЖИМАХ
Задание на курсовую работу
Анализ линейных электрических цепей в установившихся режимах
- Исходные данные задания 1.
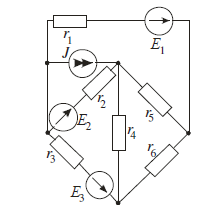
- Исходные данные задания 2.
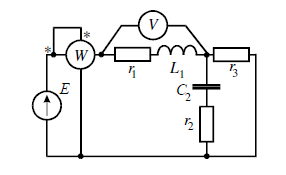
- Исходные данные задания 3.
Uфг = 127 В; RA = 40 Ом; XCA = 50 Ом; RB = 55 Ом; XLB = 60 Ом; RC = 20 Ом;
- Исходные данные задания 4.
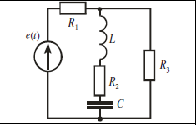
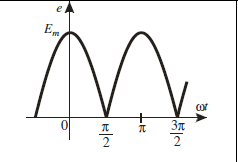
Дата выдачи задания Срок защиты курсовой работы «___» _________________ 20___ г. «___» ________________ 20___ г.
Руководитель работы Исполнитель
Доктор педагогических наук,
кандидат технических наук, профессор студент группы 12 ЭЭ(б) – 2
__________________ Б.К.Жумашева _______________Е.Д.Александров
Содержание
Введение………………………………………………………………………………....
- Задание №1. Анализ линейных электрических цепей
в установившихся режимах………………………………………………………………
- Задание №2. Анализ линейной электрической цепи
синусоидального тока в установившемся режиме……………………………………...
- Задание №3. Анализ трехфазных цепей при различных схемах
соединения нагрузки……………………………………………………………………...
- Задание №4. Анализ линейной электрической цепи
с несинусоидальным источником………………………………………………………..
Заключение…………………………………………………………………………..…..
Список использованных источников……………………………………………..
Введение
MathCad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы.
Основные возможности:
MathCad содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции со скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.
Среди возможностей MathCad можно выделить:
- Решение дифференциальных уравнений, в том числе и численными методами
- Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.)
- Использование греческого алфавита, как в уравнениях, так и в тексте
- Выполнение вычислений в символьном режиме
- Выполнение операций с векторами и матрицами
- Символьное решение систем уравнений
- Аппроксимация кривых
- Выполнение подпрограмм
- Поиск корней многочленов и функций
- Проведение статистических расчётов и работа с распределением вероятностей
- Поиск собственных чисел и векторов
- Вычисления с единицами измерения
- Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров
[1]
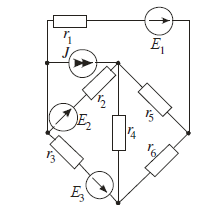
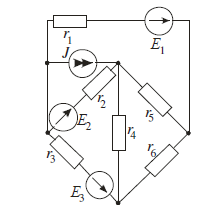
Задание №1. Анализ линейных электрических цепей
в установившихся режимах.
Исходные данные задания.
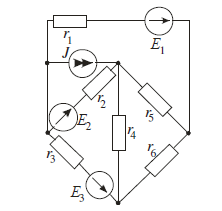
- Законы Кирхгофа.
Составим общее уравнение законов Кирхгофа.
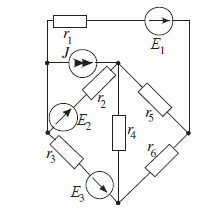
Составим матрицу по I и II законам Кирхгофа и найдем токи способом обратной матрицы.


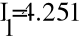
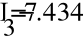
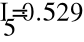
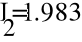
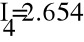
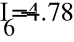
- Баланс мощности.
Проверим найденные значения токов, составив баланс мощности.


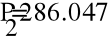
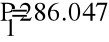

- Метод узловых потенциалов.
Заземлим узел 4 и составим уравнение по методу узловых потенциалов.
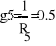
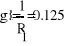
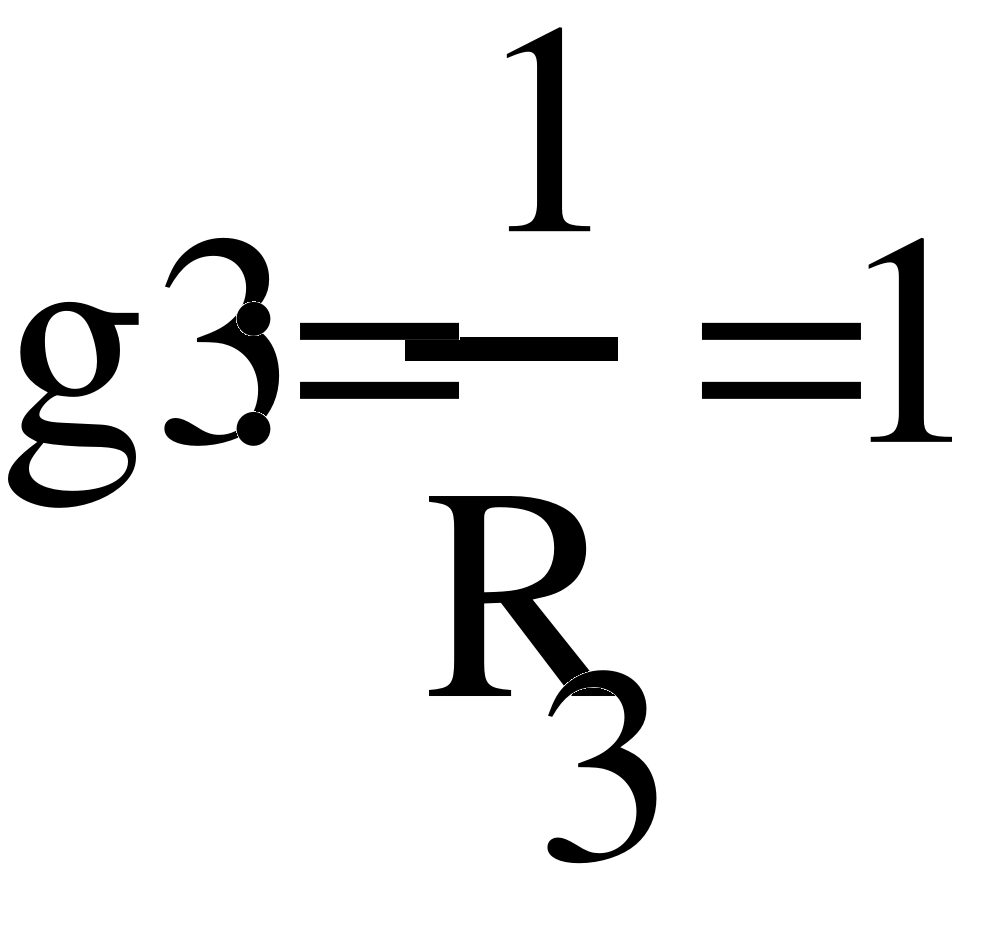
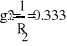
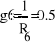
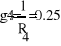

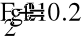
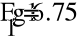
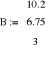
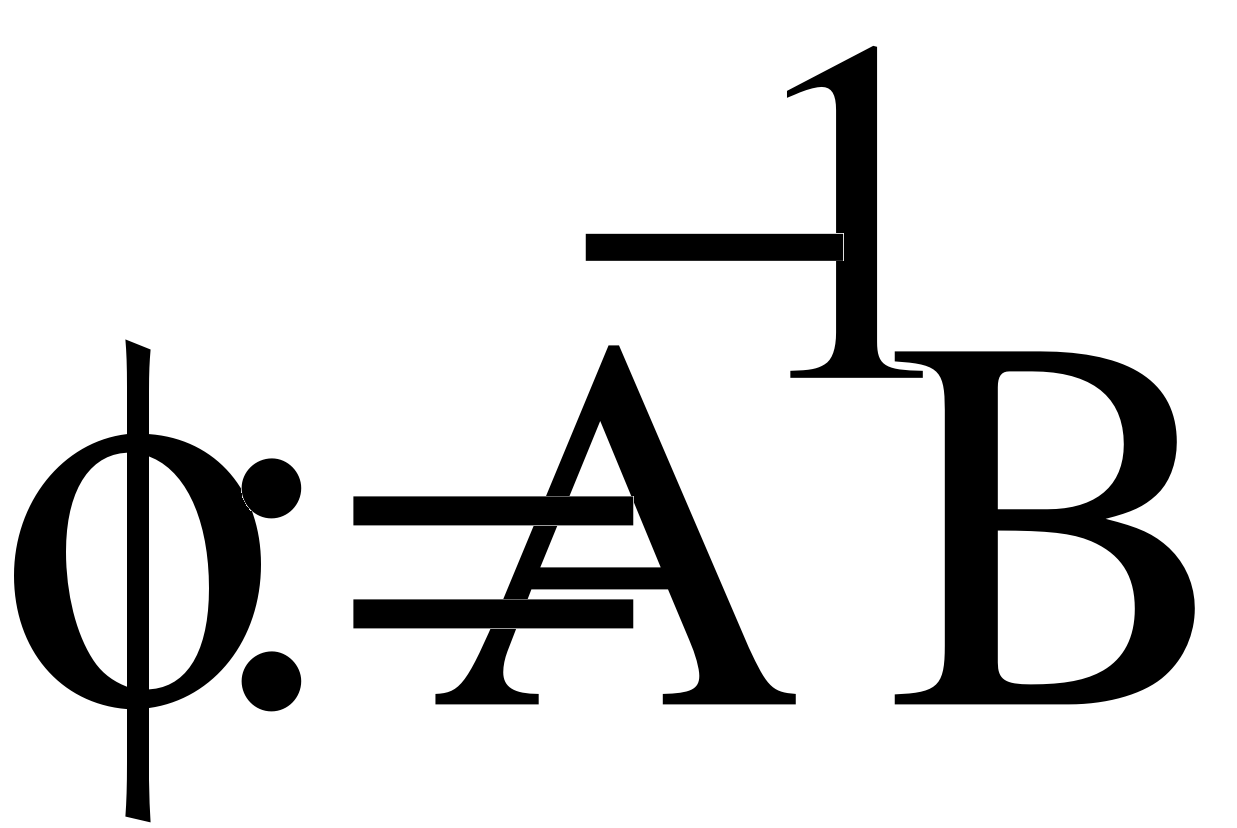
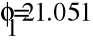

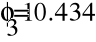
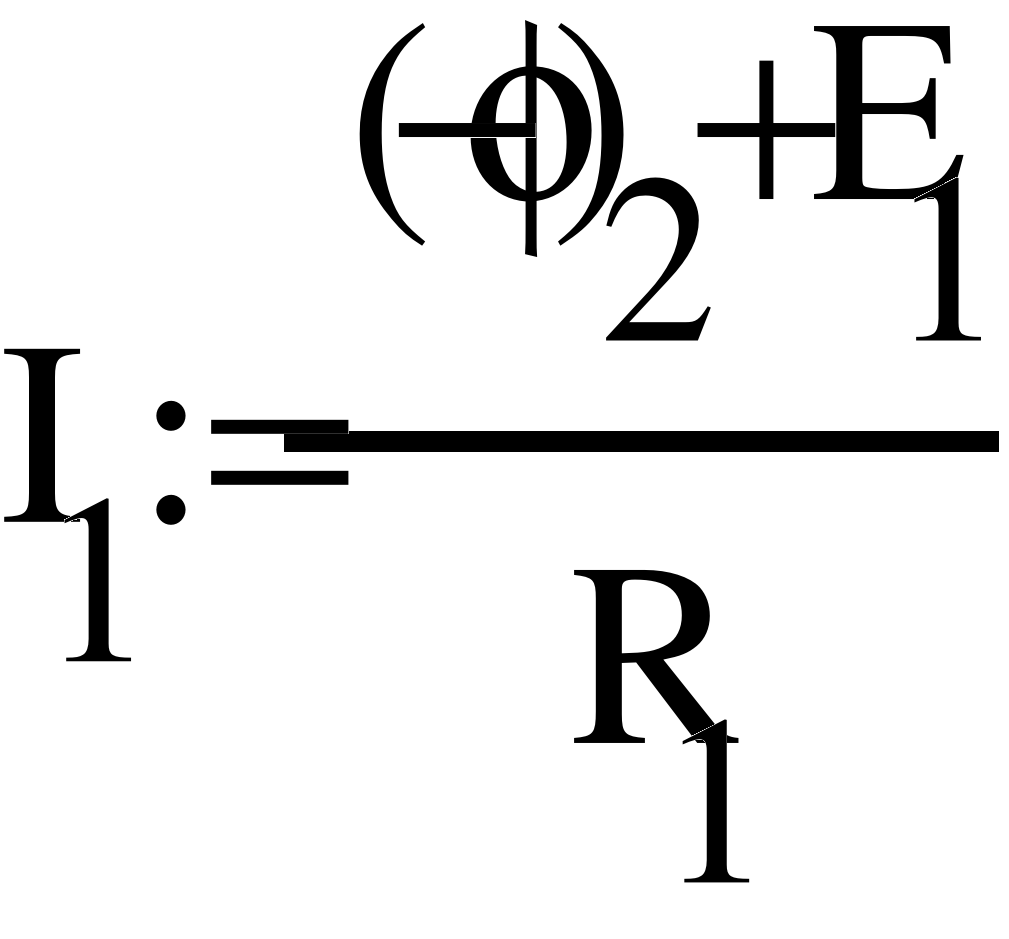
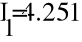
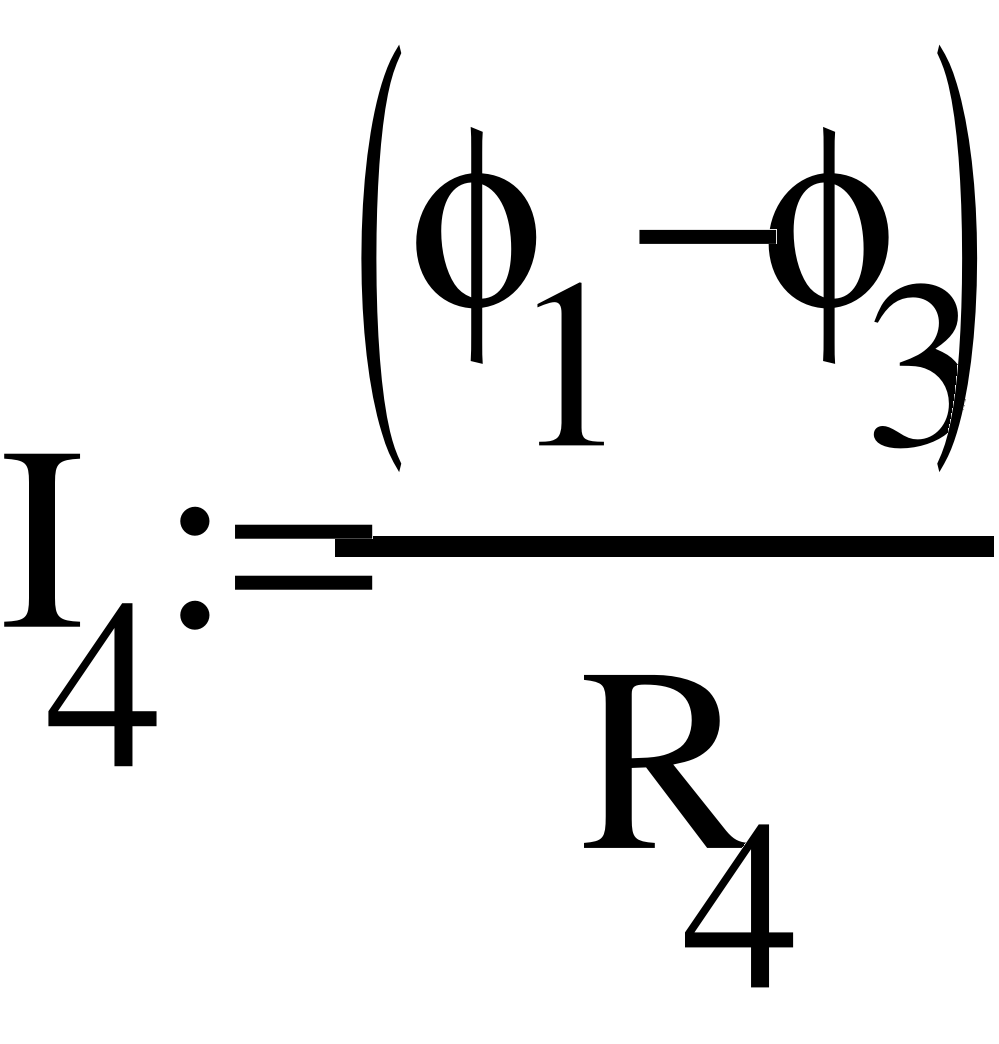
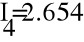
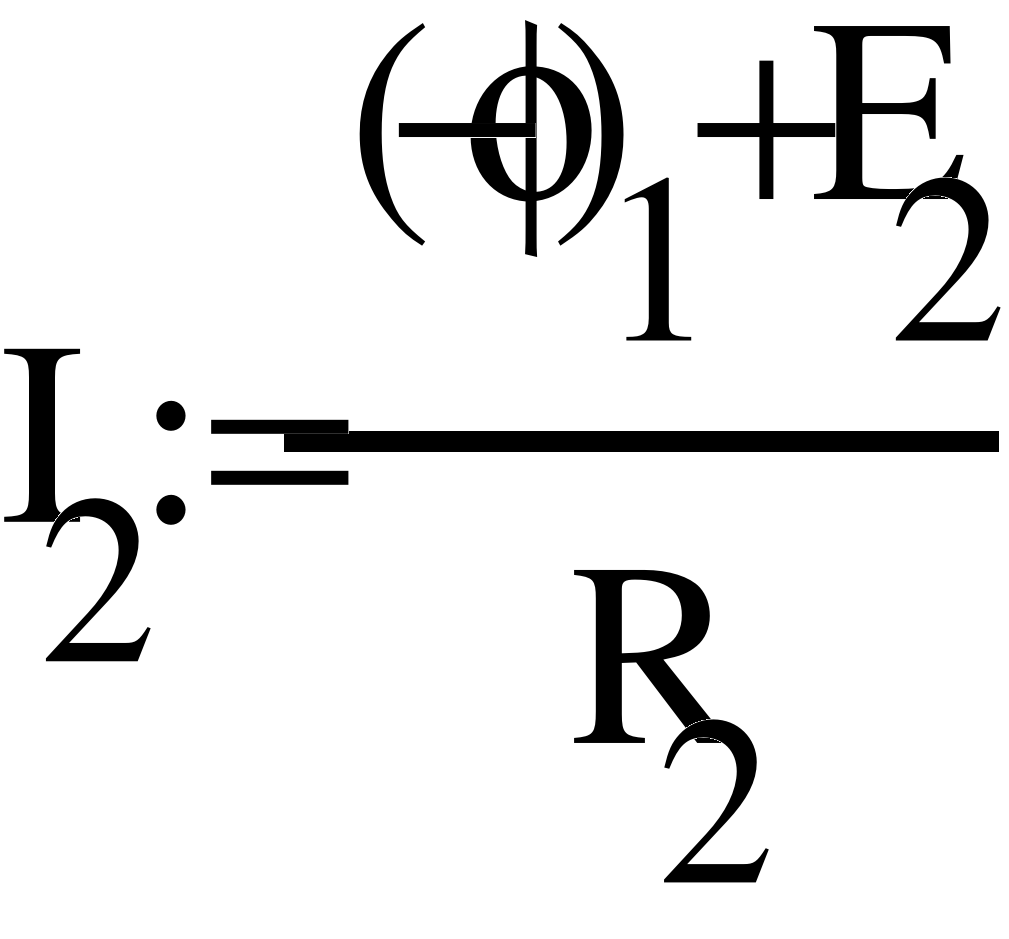
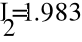
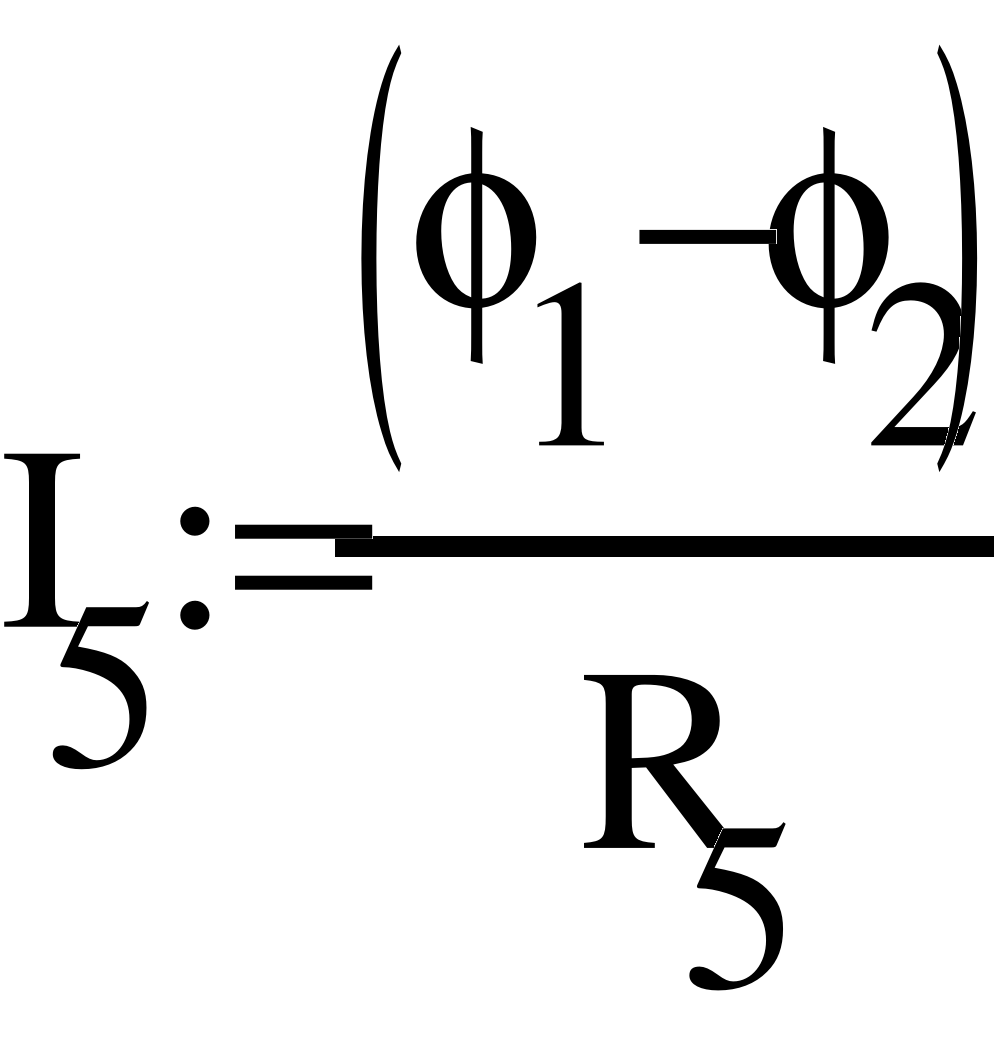
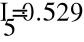
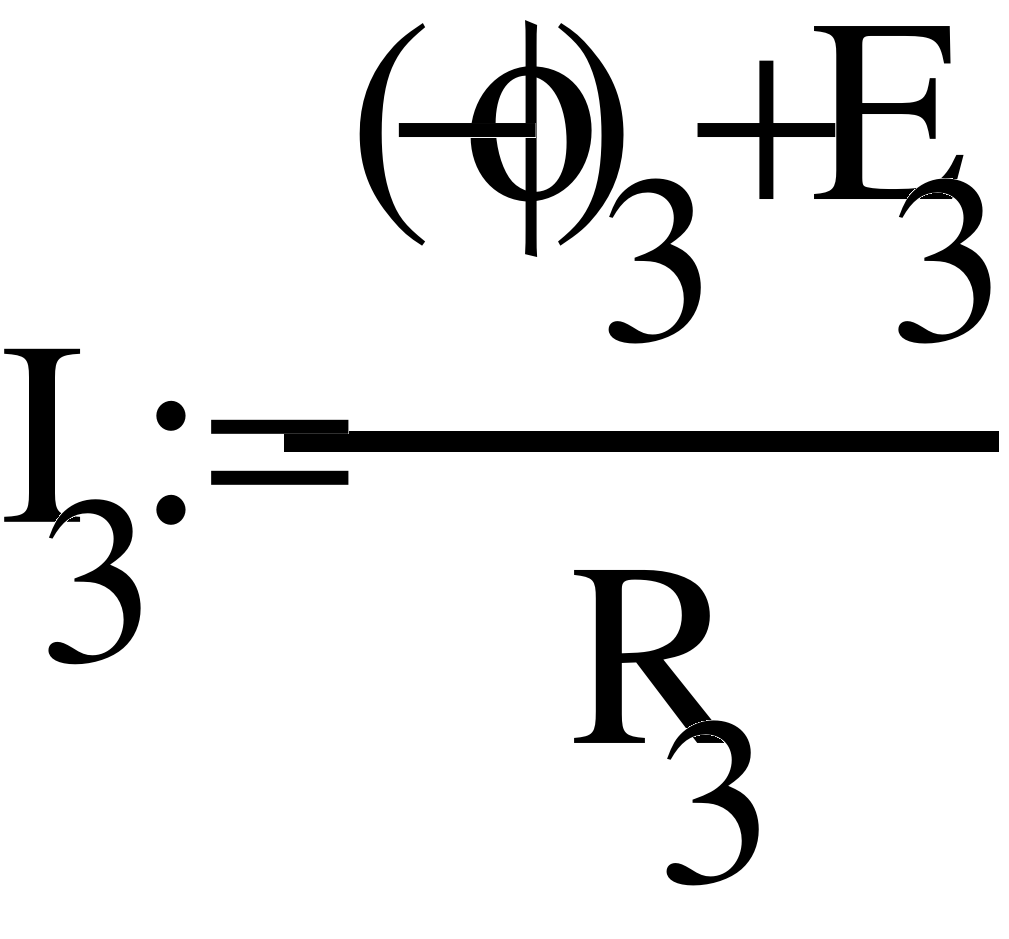
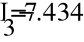
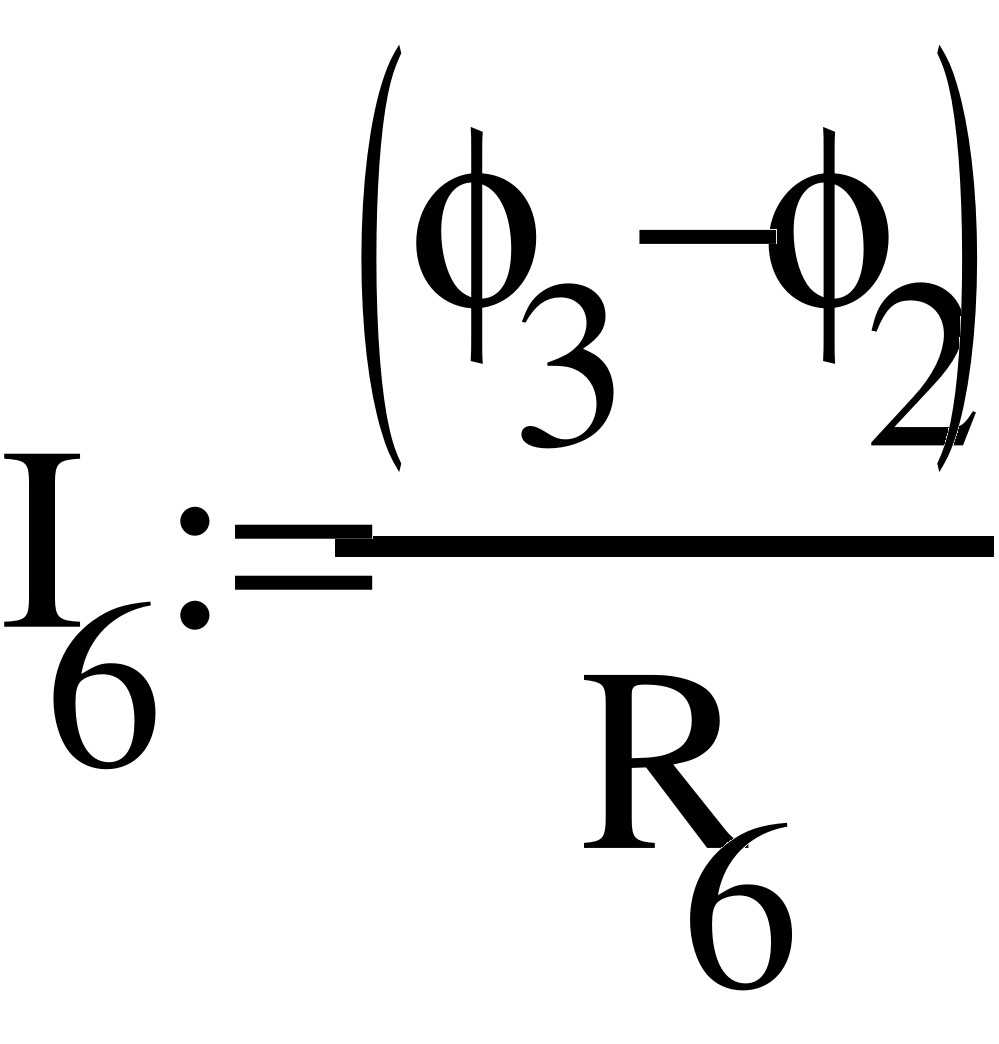
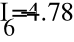
- Метод контурных токов.
Составим систему уравнений по второму закону Кирхгофа.
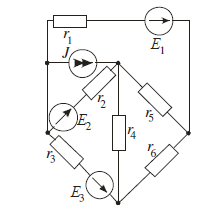
Составим матрицу по методу контурных токов. Найдем токи с помощью обратной матрицы.
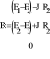

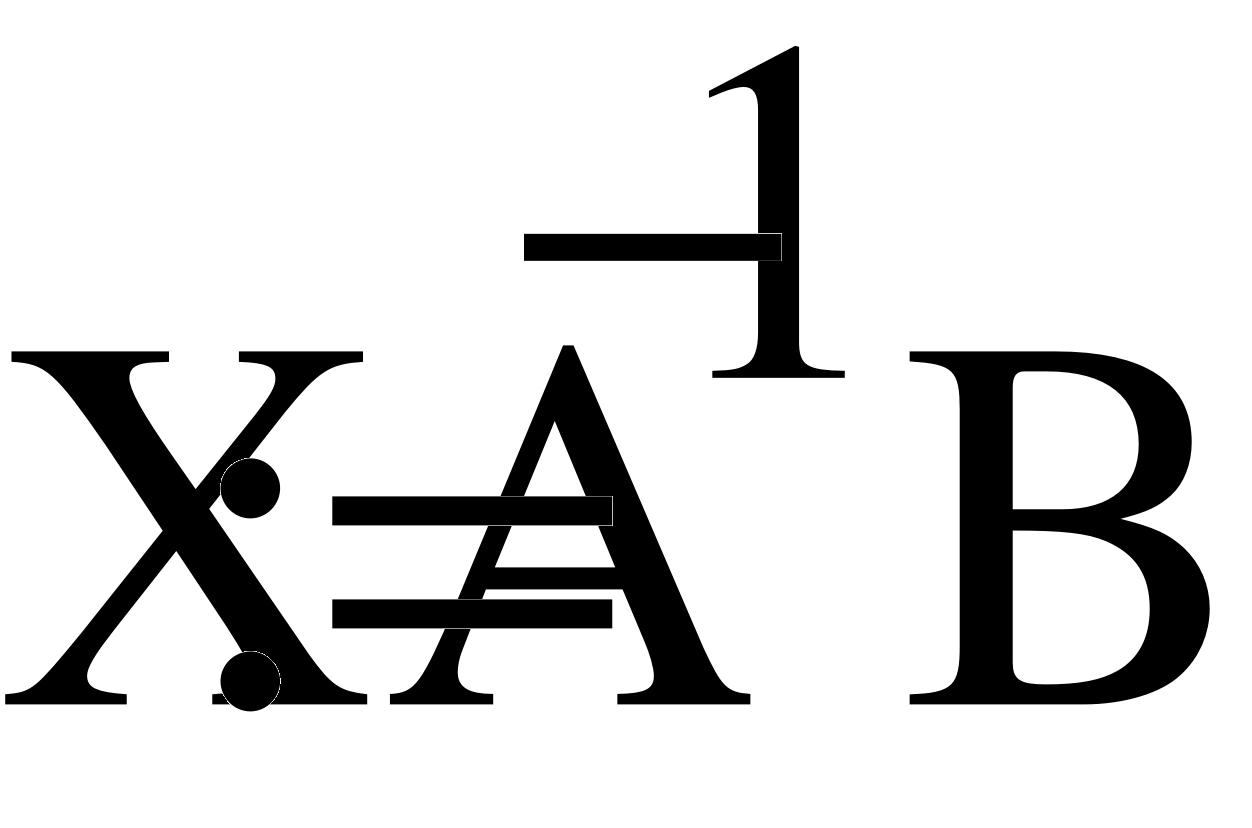
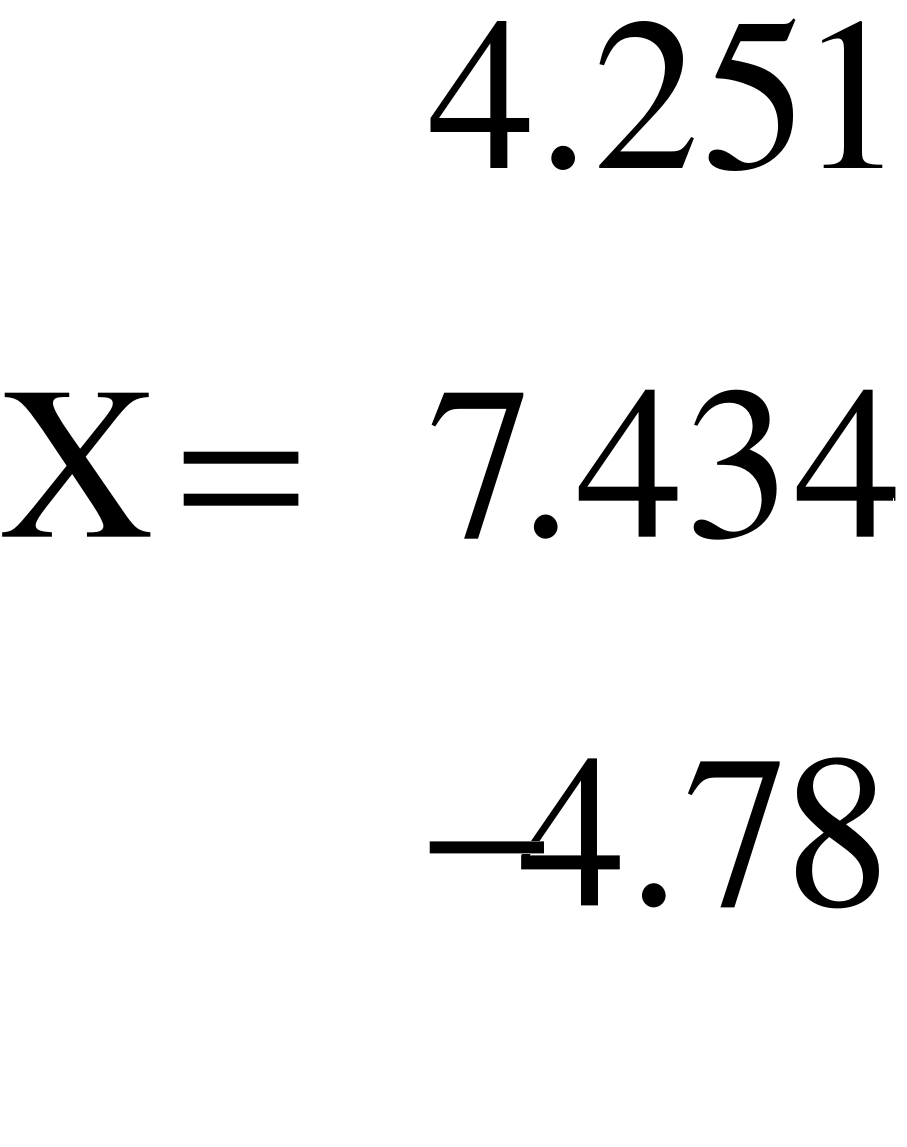
X1=Iк1 Х2=Ik2 X3=Ik3
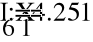
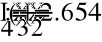
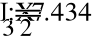
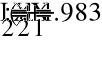
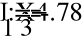
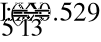
- Метод эквивалентных преобразований.
Преобразуем треугольник 456 в эквивалентную звезду.
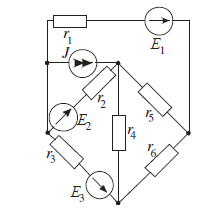
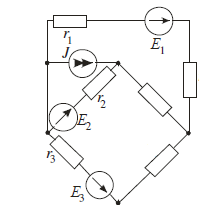
Преобразуем источник тока J в источник ЭДС E5. Сложим последовательные сопротивления R1 и R56, чтобы получить сопротивление R156. Сложим сопротивления R46 и R3, чтобы получить сопротивление R346.

Сложим источники ЭДС E2 и E5.
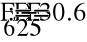
Сложим параллельные источники ЭДС Е6 и Е3 и получим источник ЭДС Е7. Сложим параллельные сопротивления R245 и R346 в сопротивление R8.
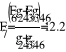
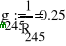
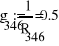
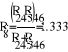
Найдем искомый ток по второму закону Кирхгофа.
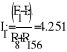
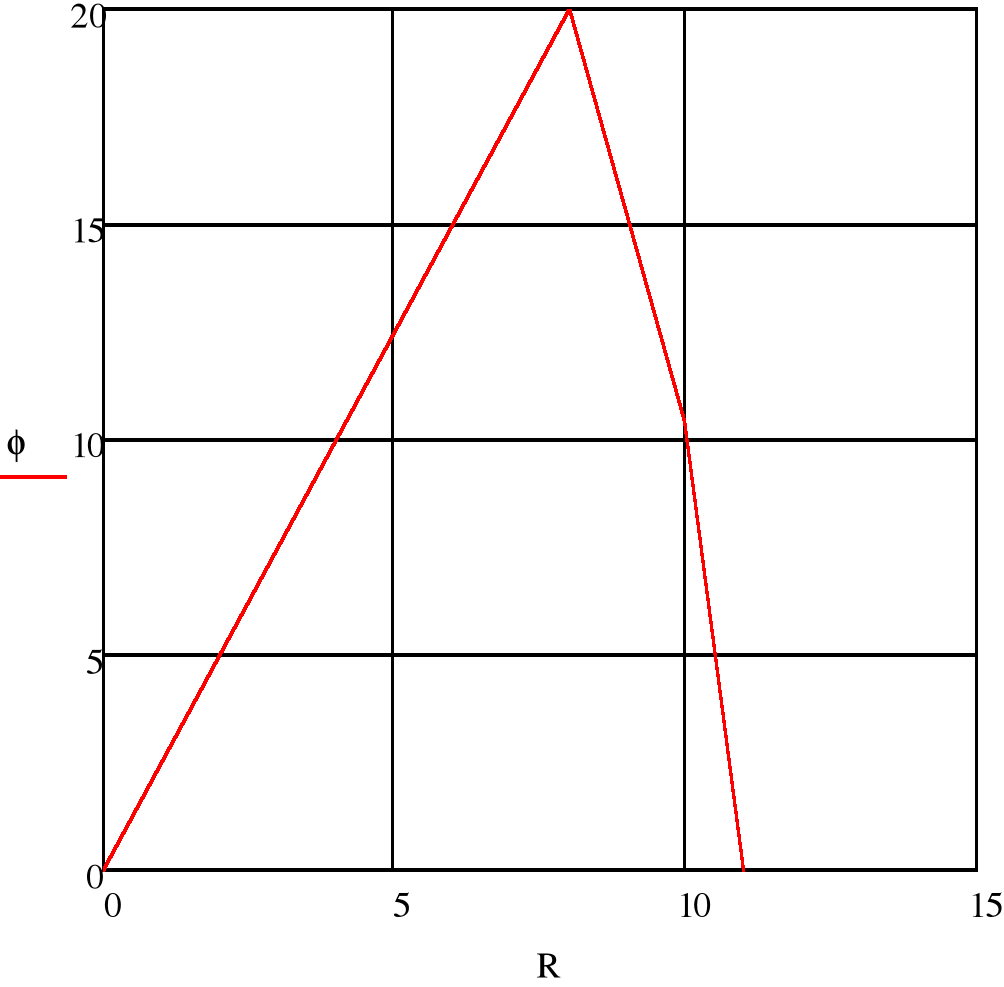
- Потенциальная диаграмма.
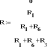
Заземлим узел 1. Составим матрицу сопротивлений и матрицу потенциалов. Посмтроим график изменения потенциала по внешнему контуру.

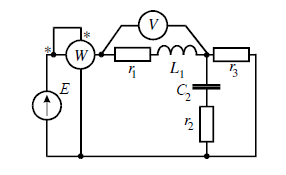
Задание №2. Анализ линейных электрических цепей синусоидального тока в установившихся режиме.
Исходные данные задания
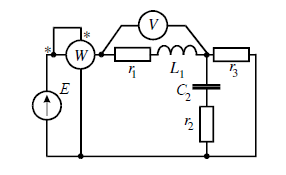
- Система уравнений в дифференциальной форме по закону Кирхгофа.
i1-i2-i3=0
i1(R1+jXl1)+i2(r2-jXc2)=E
-i2(R2-jXc2)+i3R3=0
- Закон Кирхгофа.
Запишем уравнение в общем виде и решим систему способом обратной матрицы.
i1-i2-i3=0
i1(R1+jXl1)+i2(r2-jXc2)=E
-i2(R2-jXc2)+i3R3=0

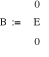
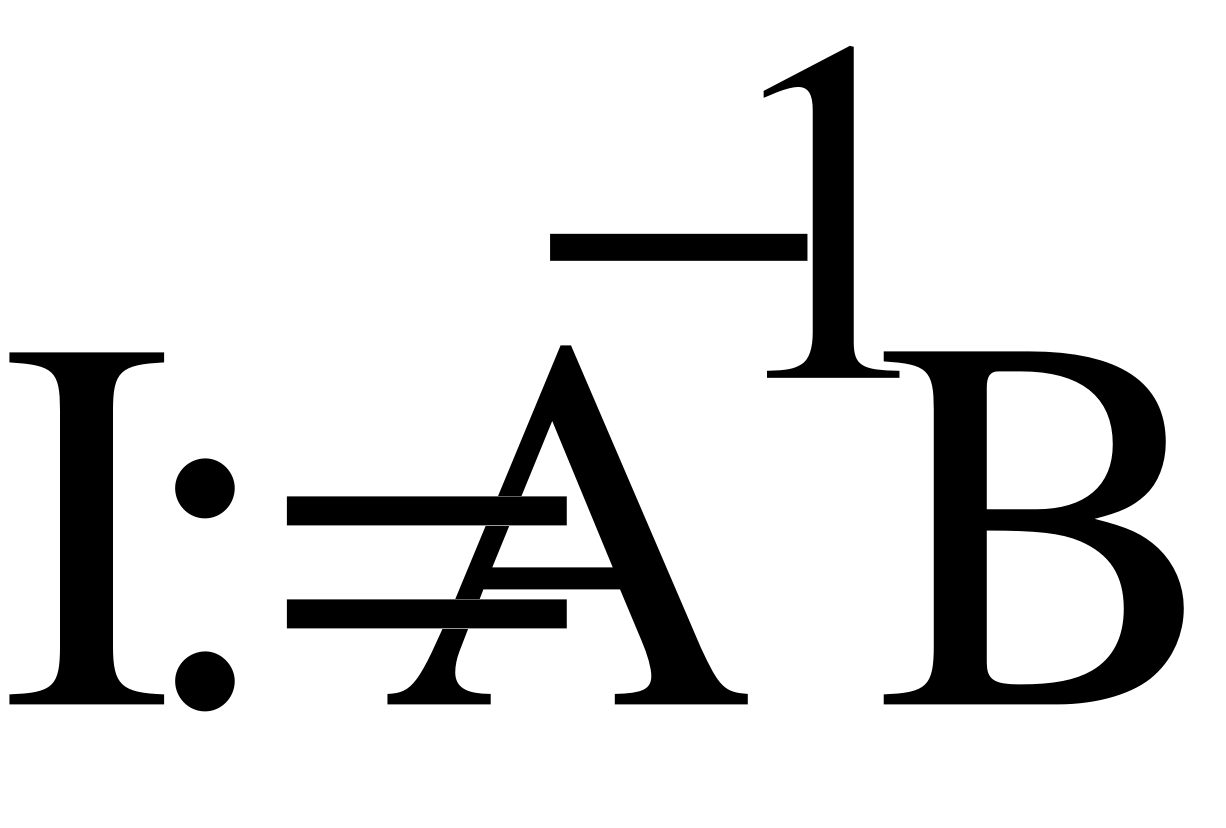
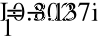
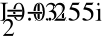
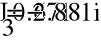
- Метод контурных токов.
Расставим направления обхода и найдем токи с помощью обратной матрицы.
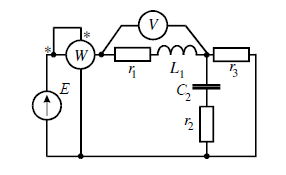
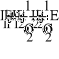
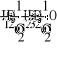

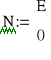
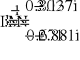
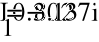
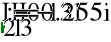
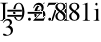
- Метод узловых потенциалов.
Расставим узлы, заземлим один из узлов и решим систему уравнений.
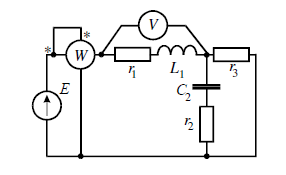
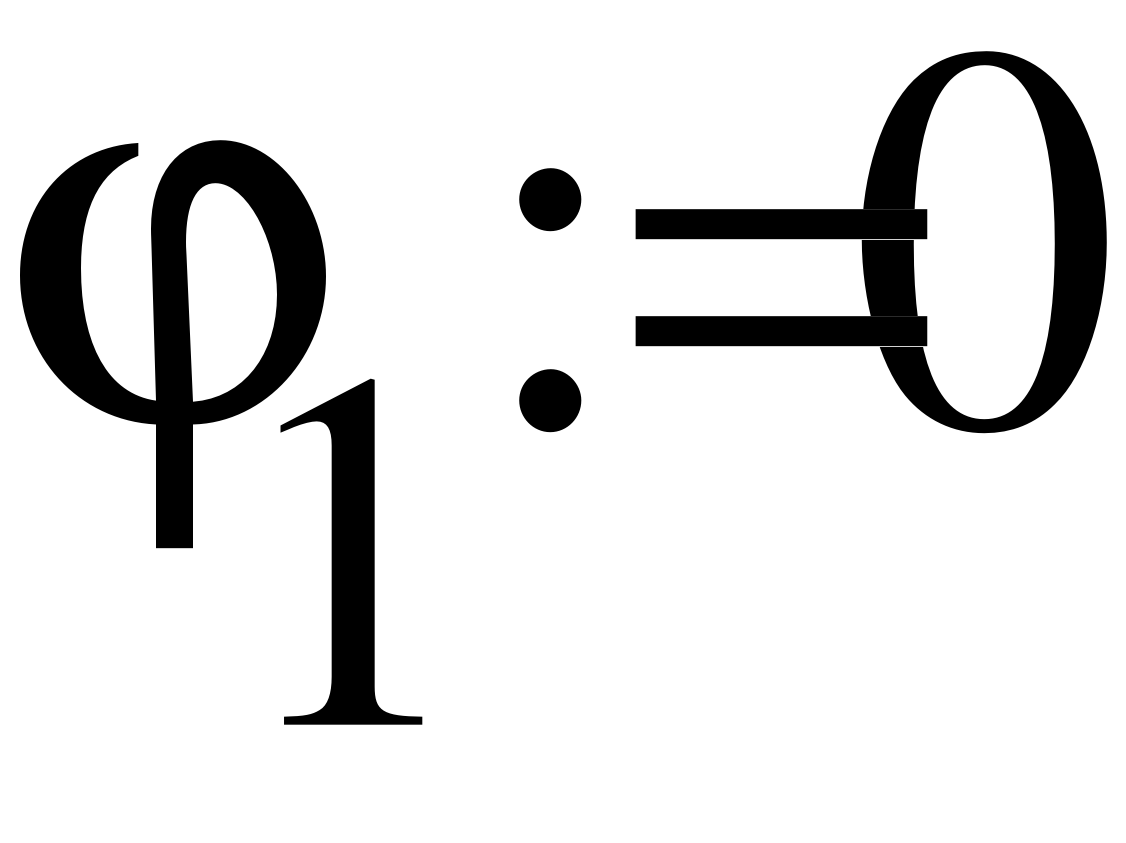
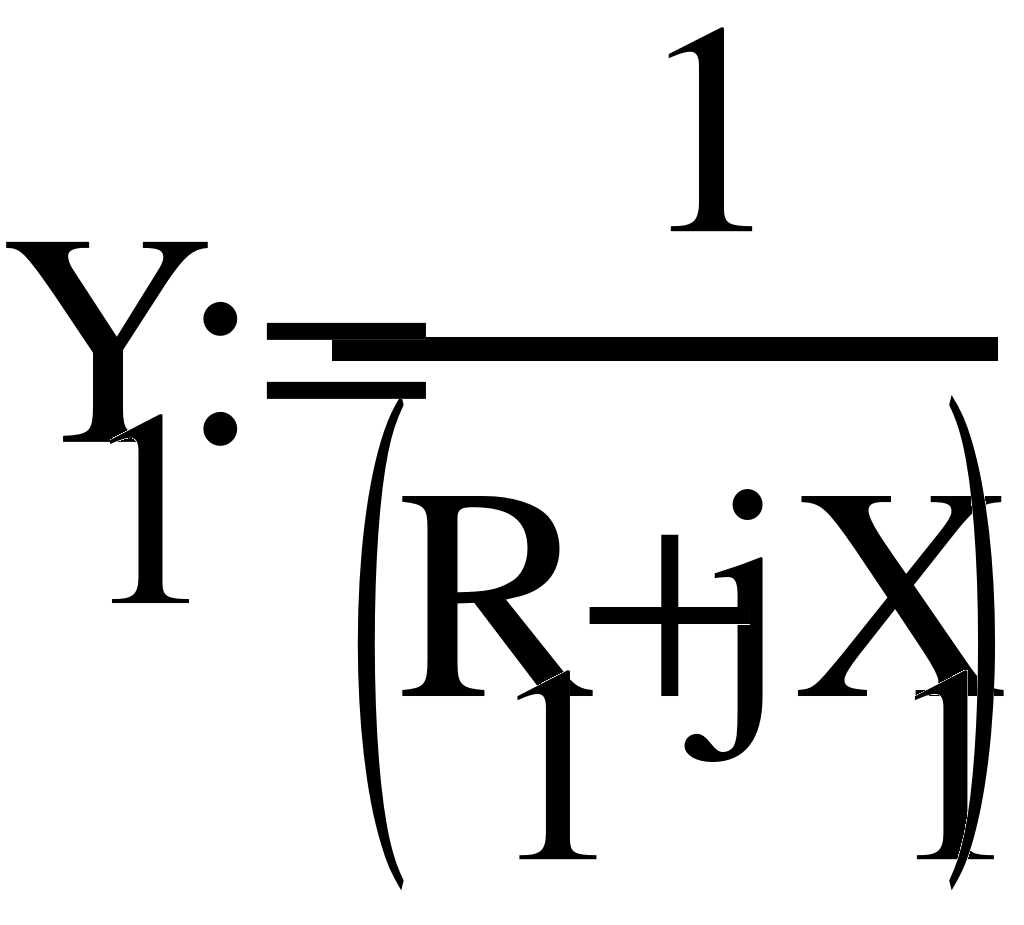
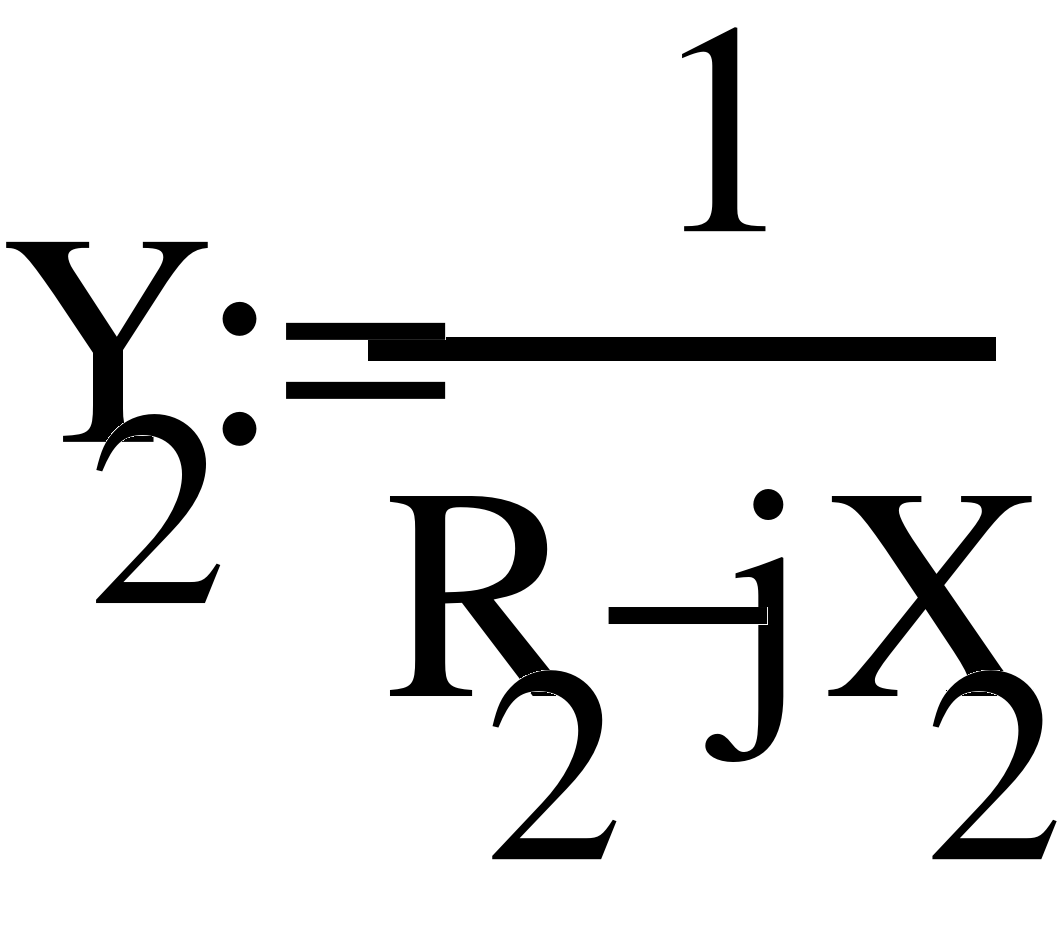
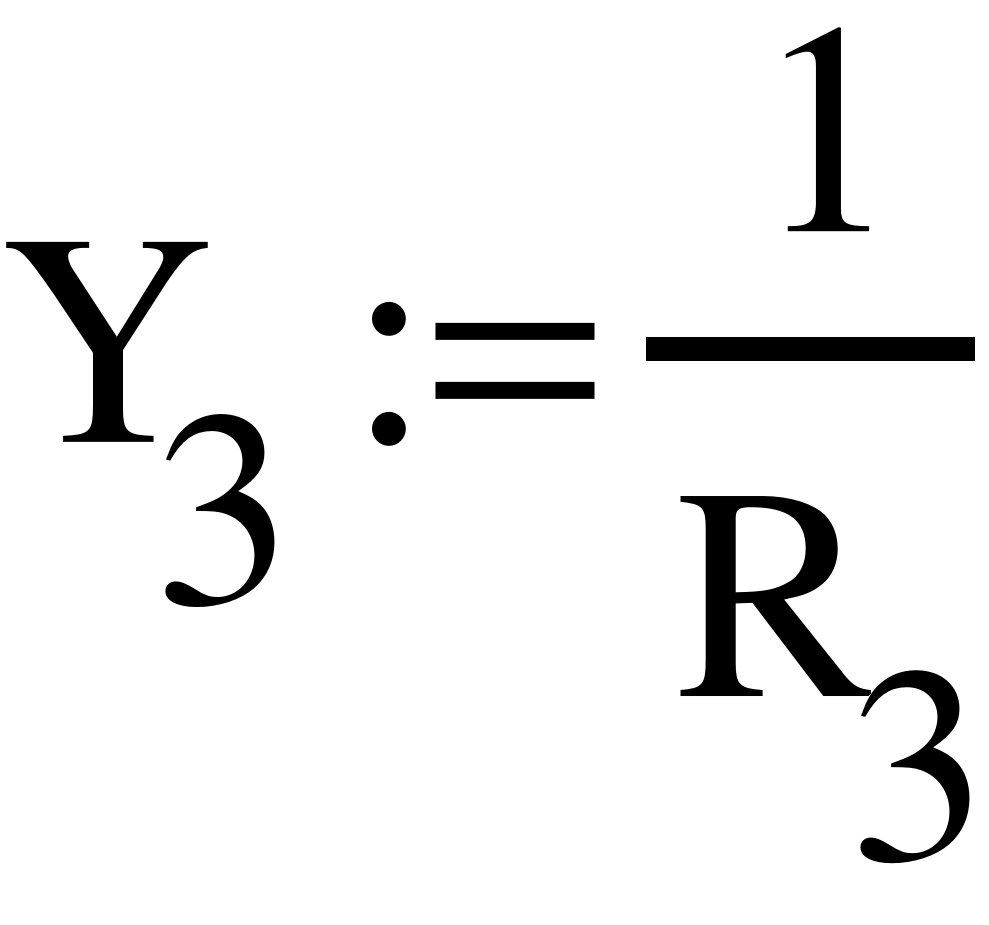
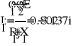
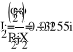
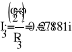
- Баланс мощностей.
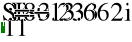
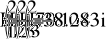
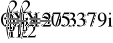
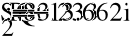
- Векторная и топографическая диаграммы.
На схеме найдем точки в цепи с разными потенциалами.
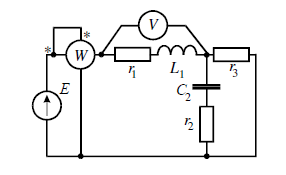
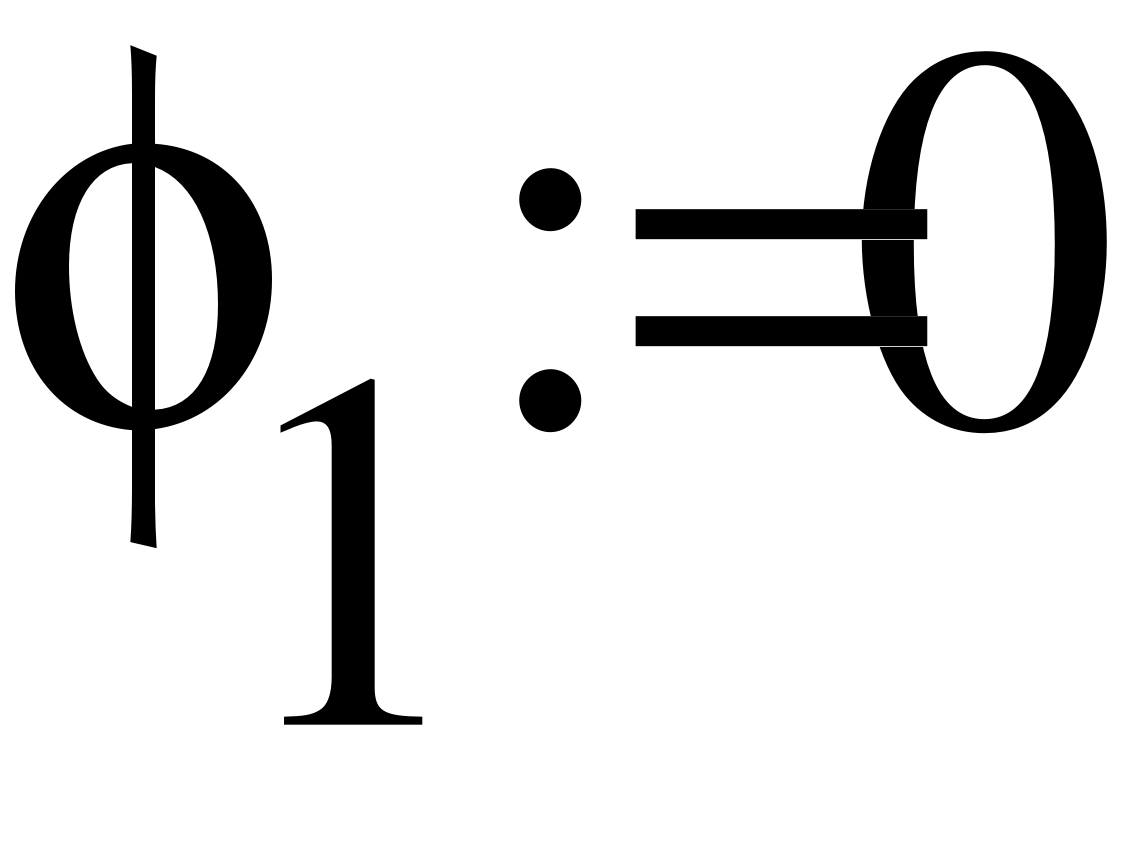
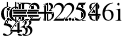


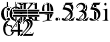
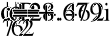
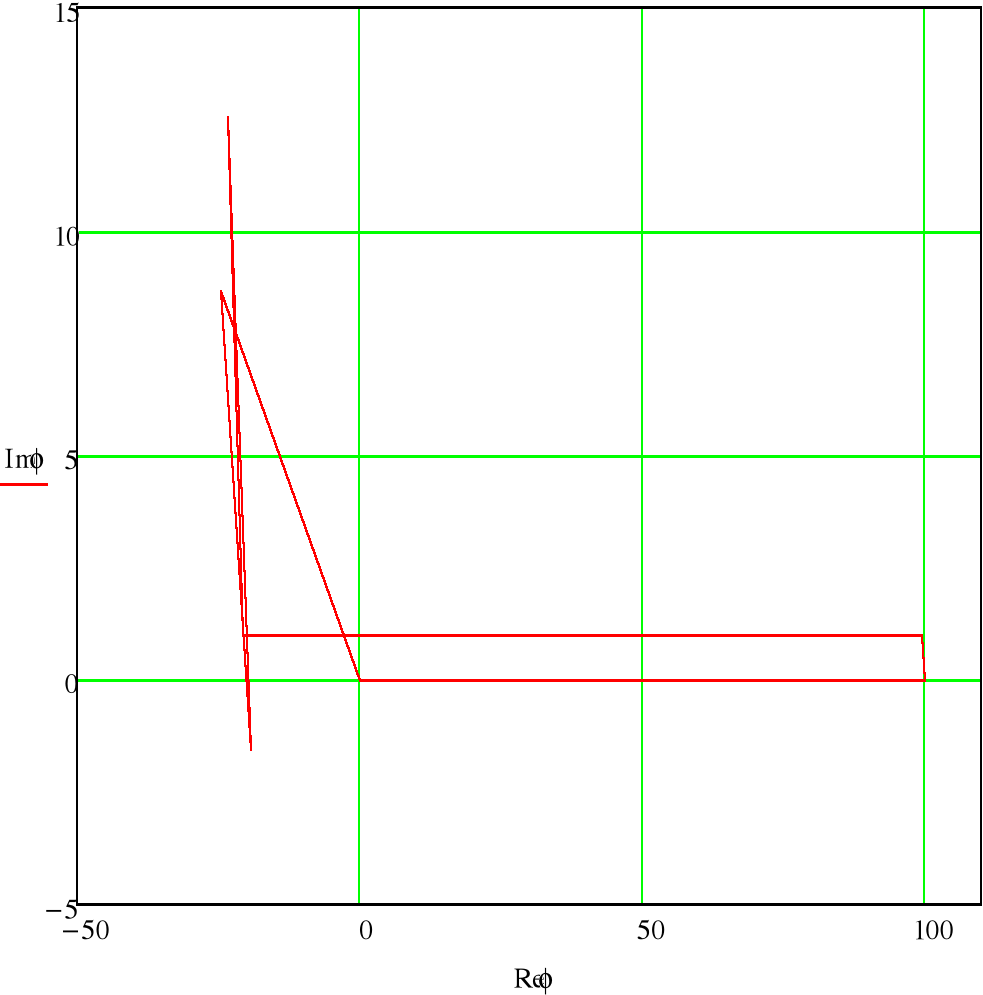
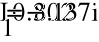
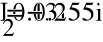
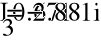


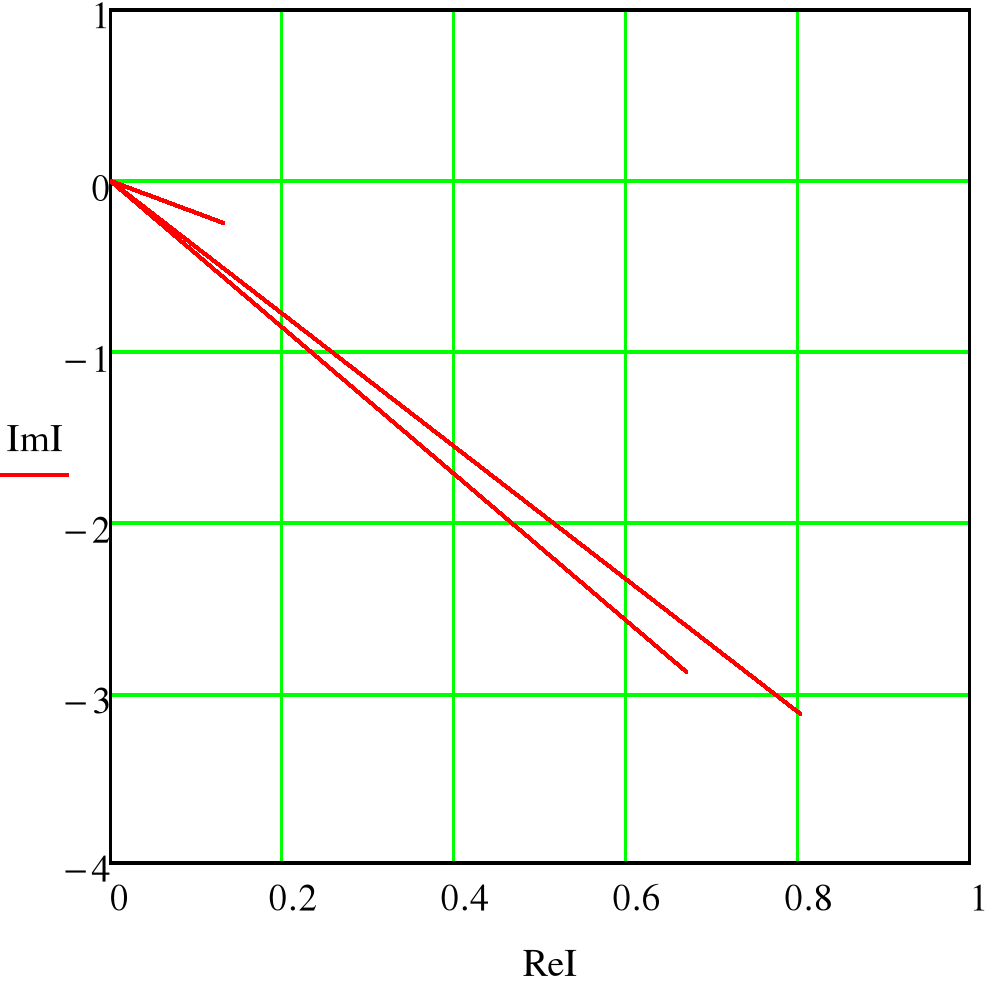
- Показания ваттметра и вольтметра.
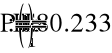
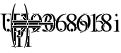
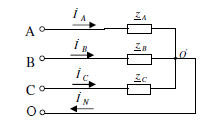
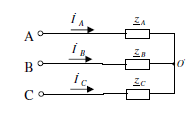
Задание №3. Анализ трехфазных цепей при различных схемах соединения нагрузки.
Исходные данные задания
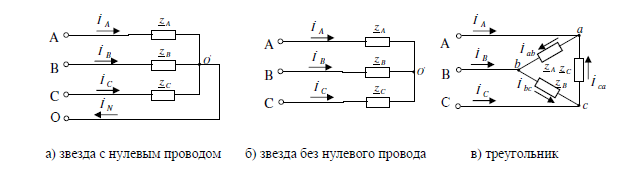
Uфг = 127 В; RA = 40 Ом; XCA = 50 Ом; RB = 55 Ом; XLB = 60 Ом; RC = 20 Ом;
- Звезда с нулевым проводом.
- Расчет токов.
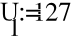
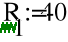
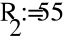
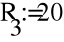
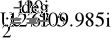
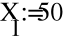
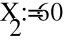
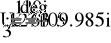
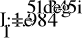
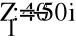
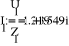
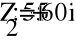
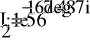
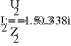
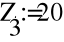
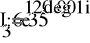
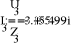
- Баланс мощностей.
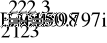
- Векторная диаграмма.
- Схема соединения «звезда».
- Расчет токов.
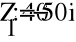
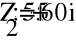
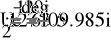
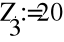
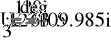
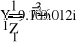
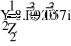
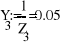
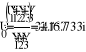
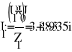
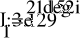
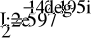

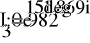
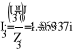
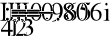
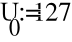
- Баланс мощностей.

- Векторная диаграмма.
с) Схема соединения «Треугольник»
- Расчет токов.
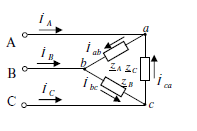
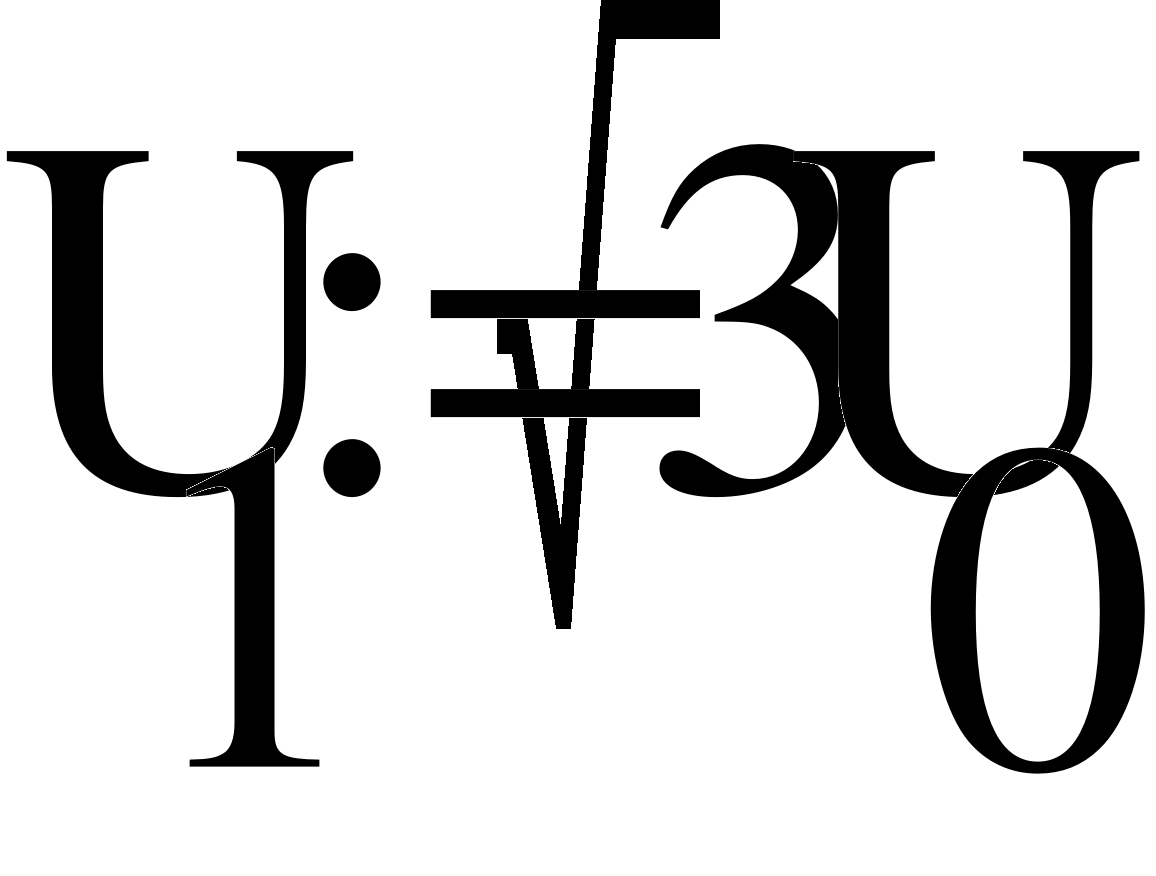
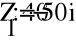
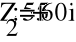
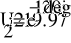
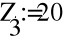
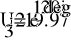
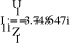
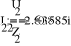
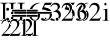
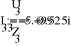
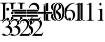
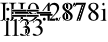

- Баланс мощностей.
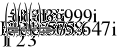
-
Векторная диаграмма.
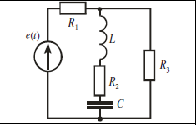
Задание №4. Анализ линейной электрической цепи
с несинусоидальным источником.
Исходные данные задания
- Представление ЭДС источника рядом Фурье.
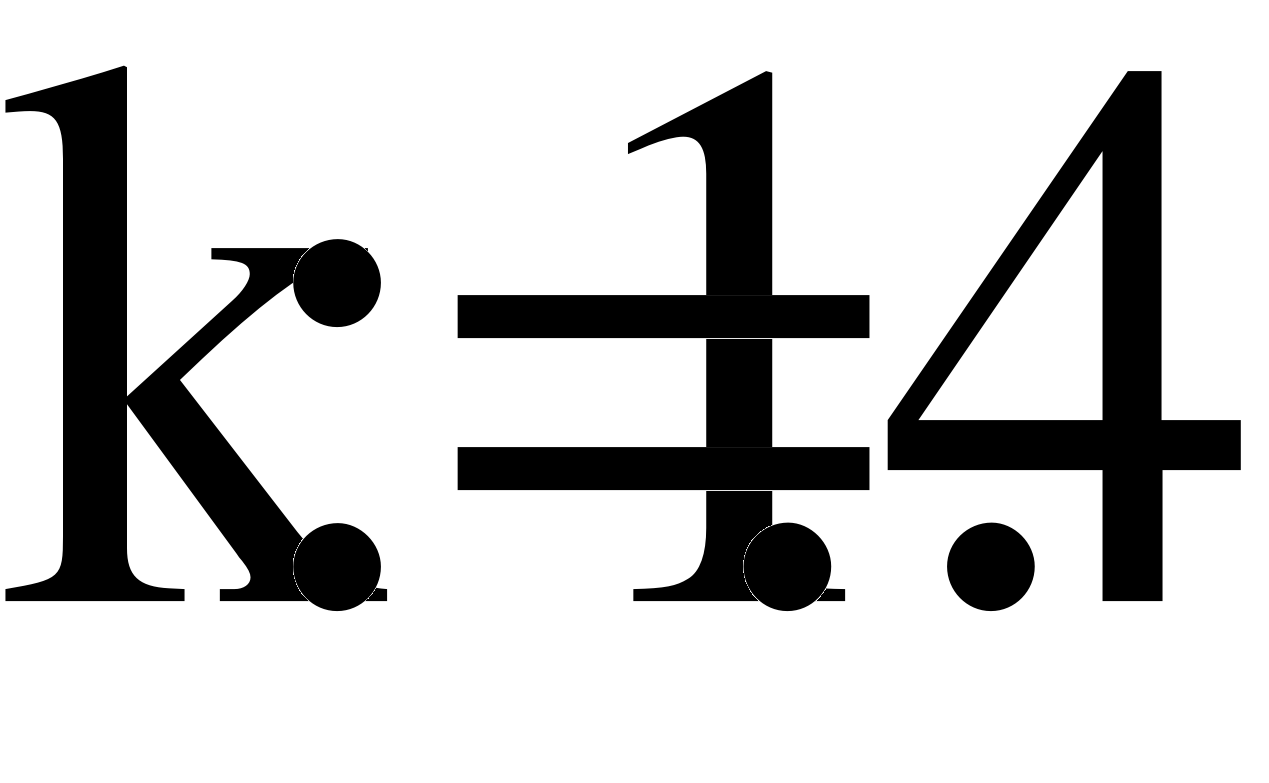
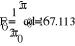
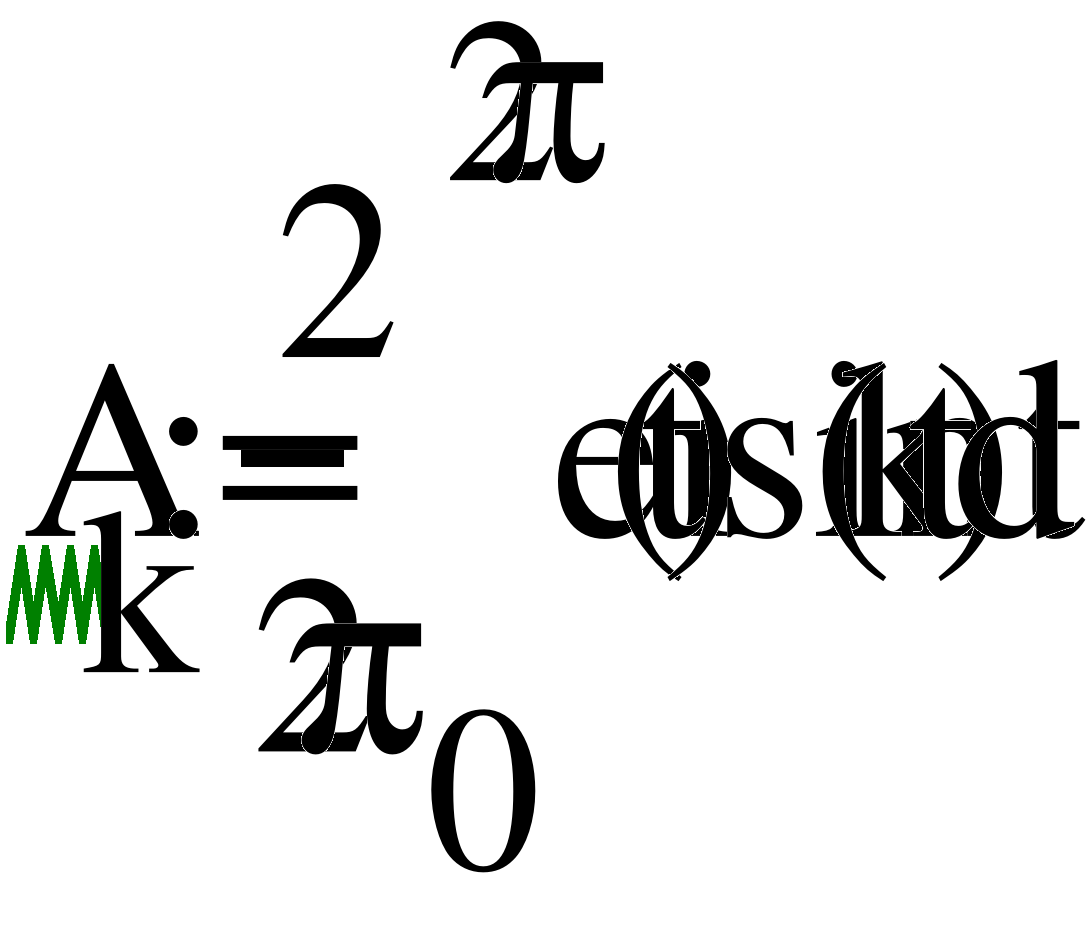
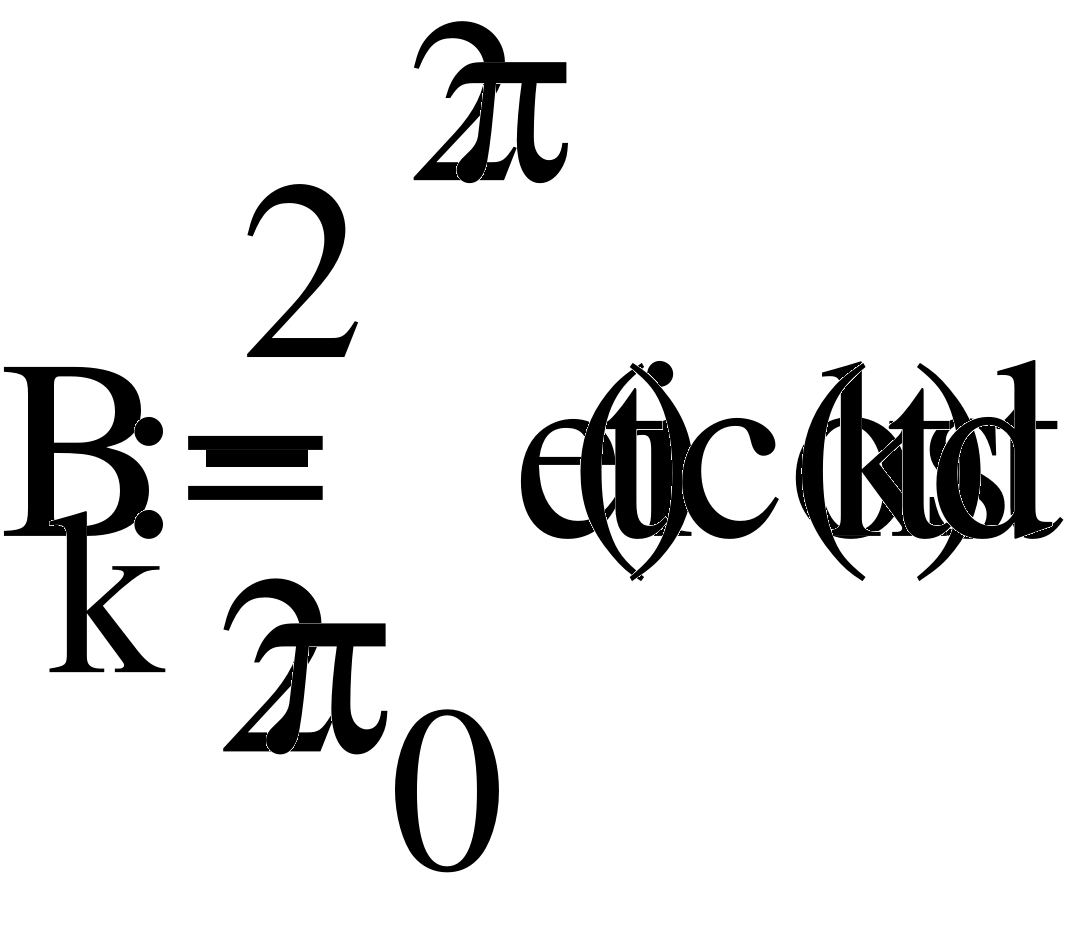

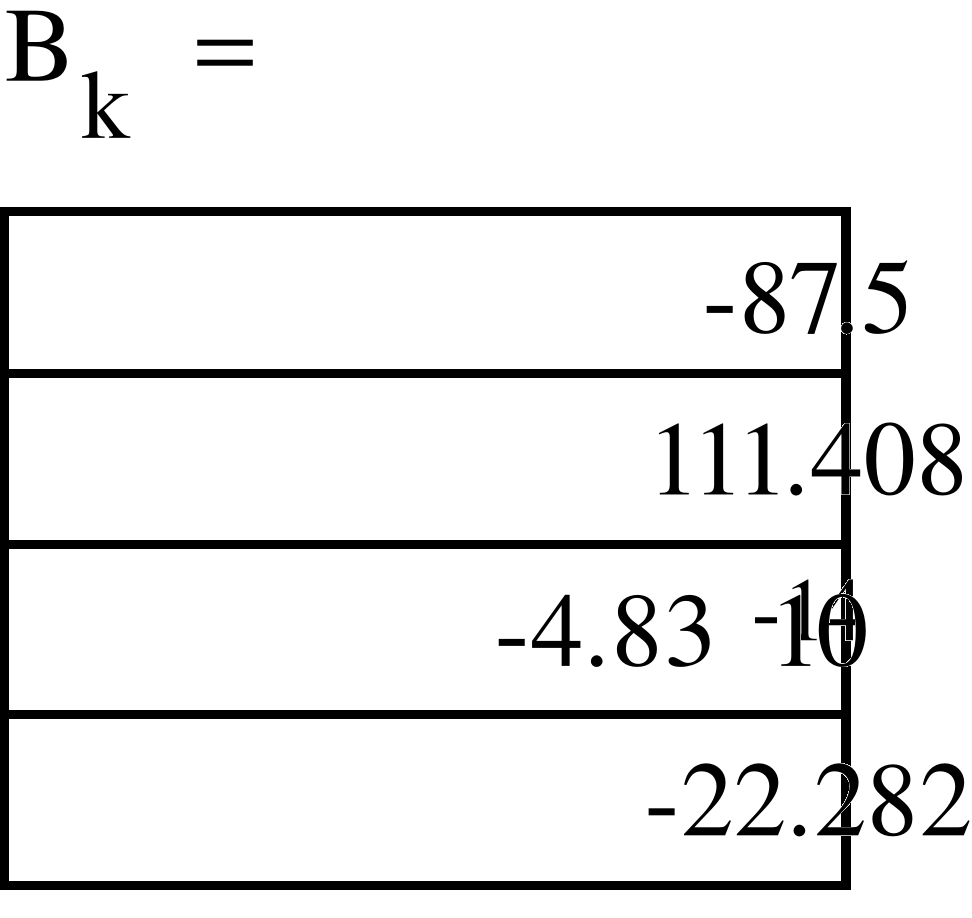



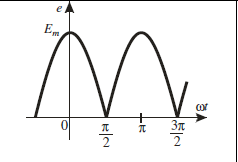
- График спектров амплитуд и начальных фаз источника.
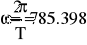

- Действующее значение ЭДС
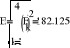
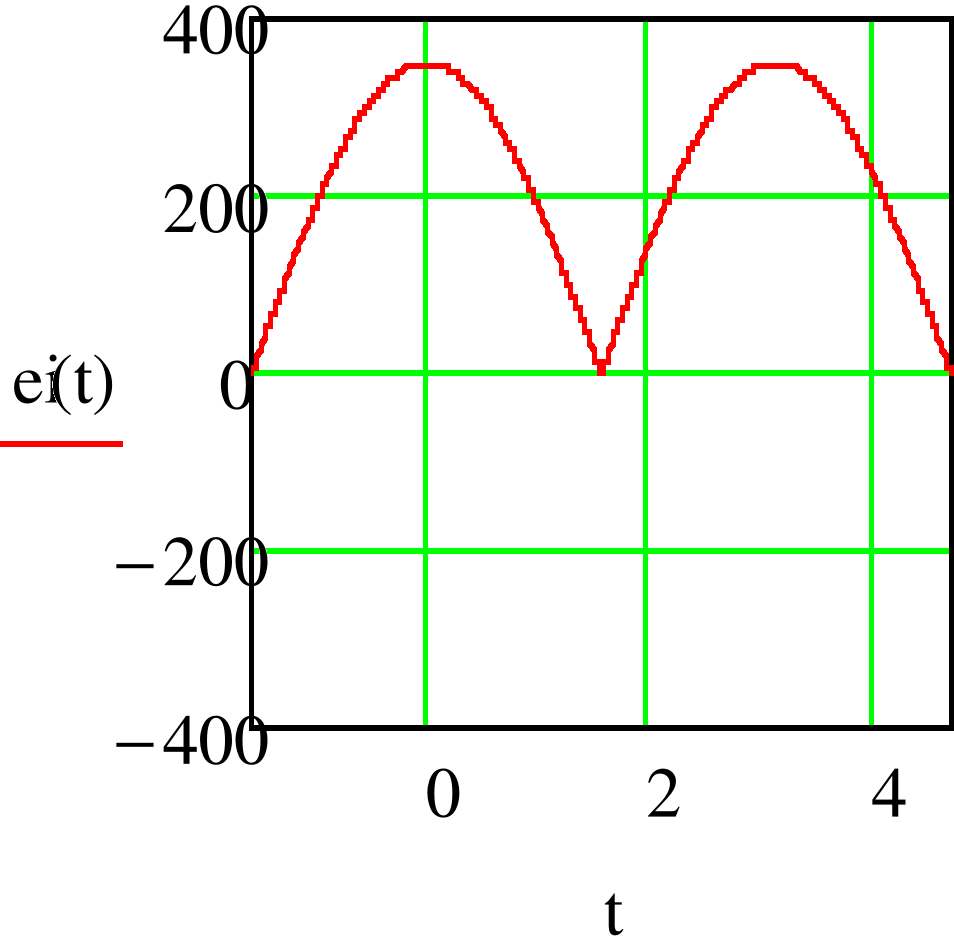
- График кривых несинусоидальных ЭДС.
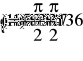
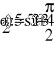
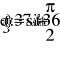
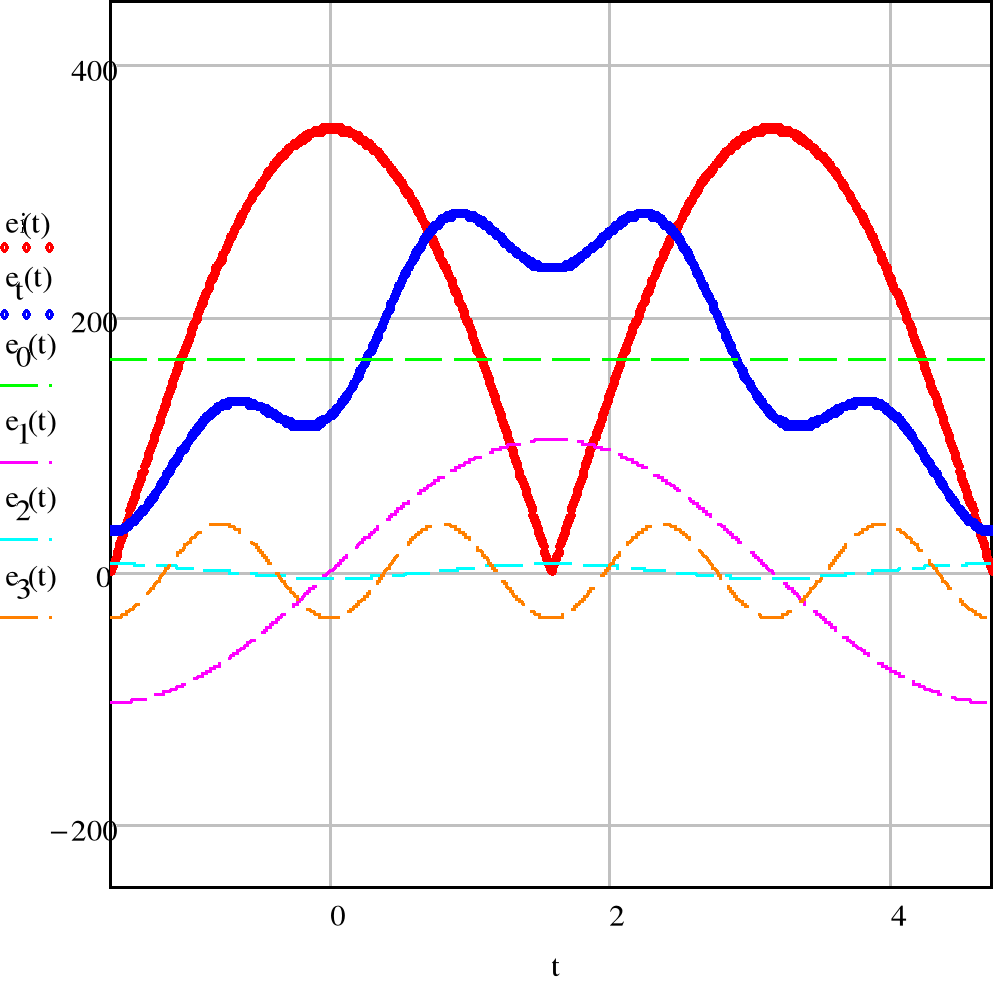
- Определение токов в ветвях.
a)
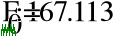
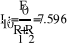
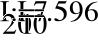
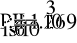
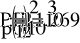
б)
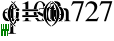
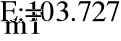
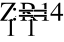
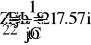
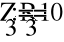
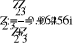
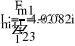
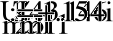
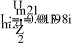
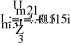
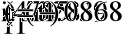
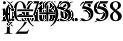
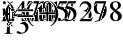
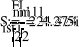
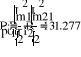
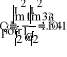
в)
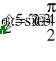
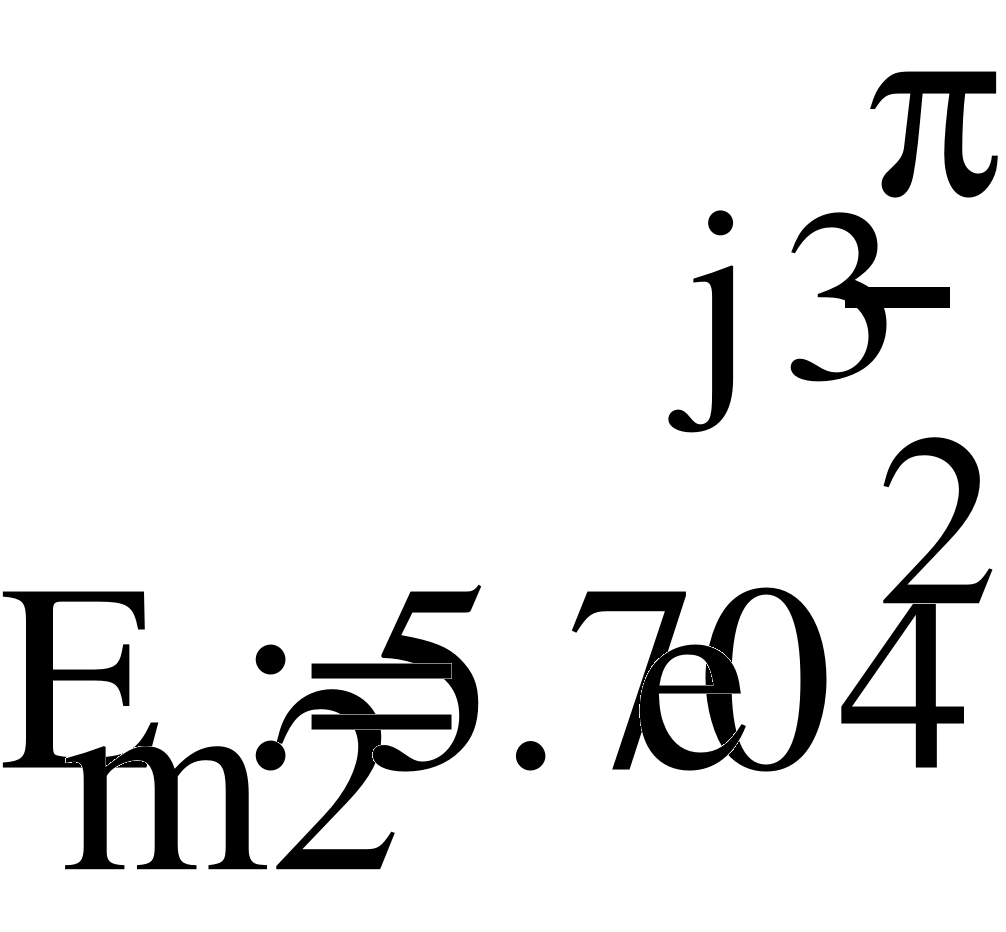
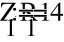
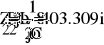
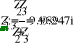
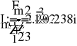
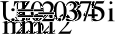
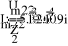
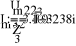


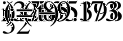
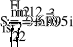

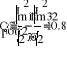
- Мгновенная форма записи токов.


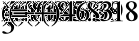
- Действующие значения токов.
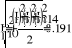
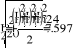

- Определение значения мощности искажения и коэффициэнта мощности в заданной электрической цепи.
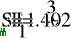
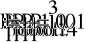
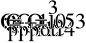
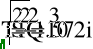
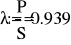
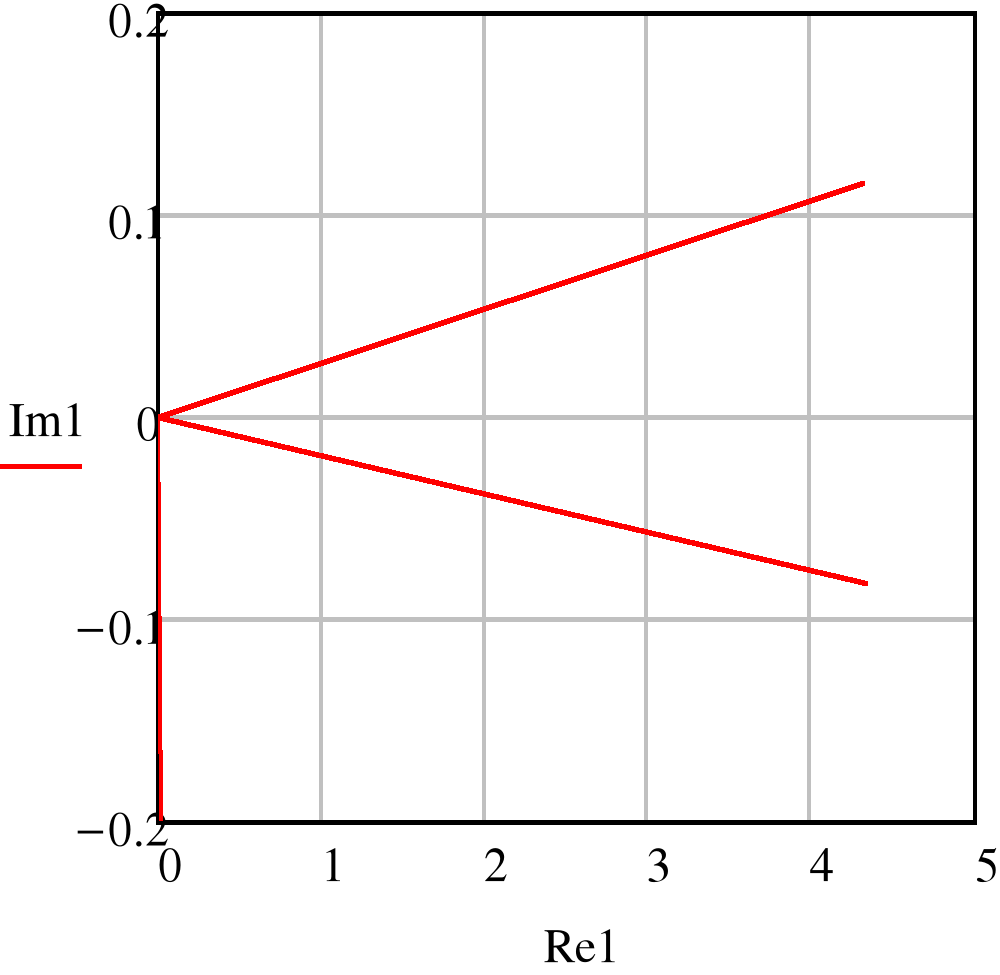
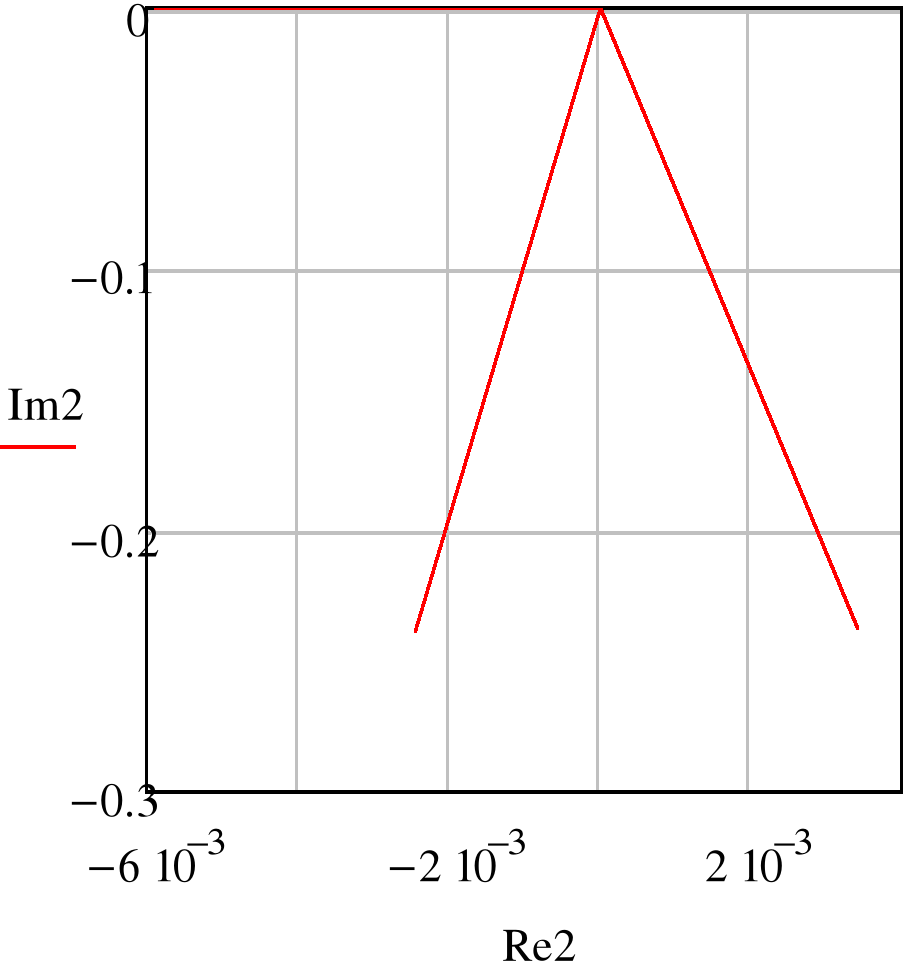
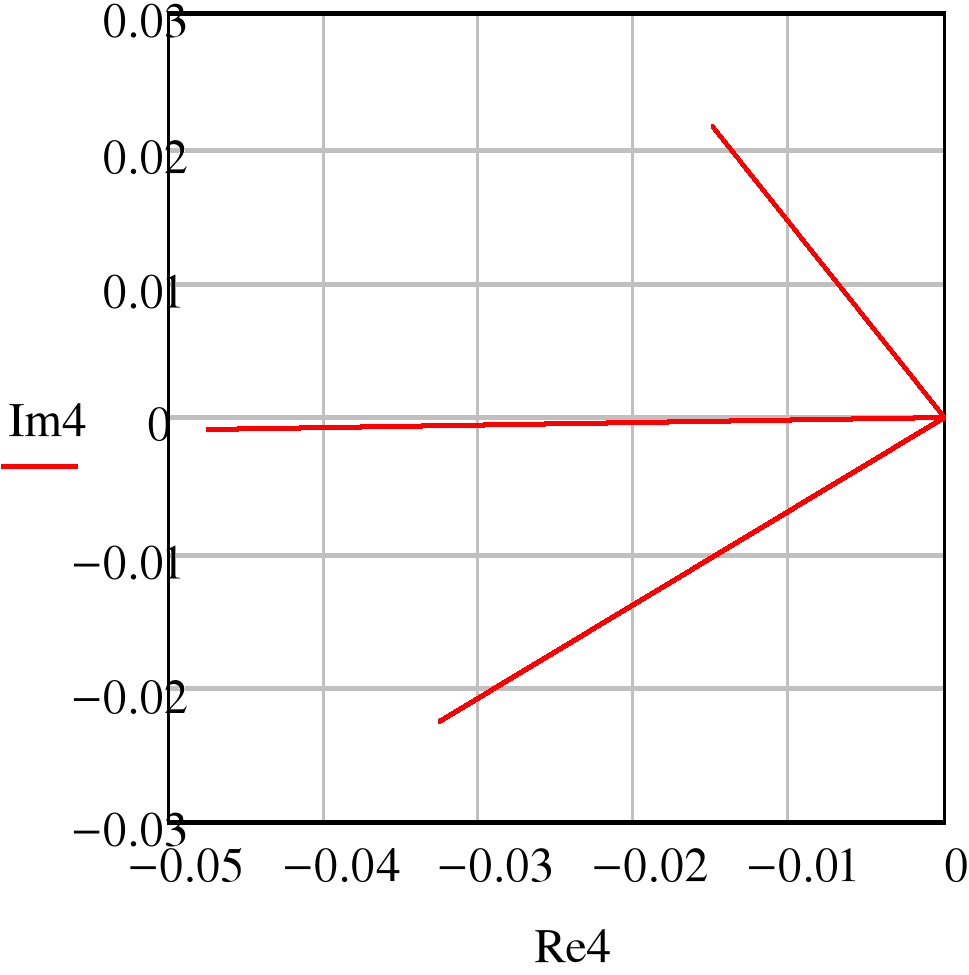
- Векторные диаграммы токов.



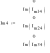
Заключение
Многие физические законы, которым подчиняются те или иные явления, могут быть записаны в виде дифференциальных уравнений. Эти уравнения описывают изменение соответствующих физических величин с течением времени и могут служить в качестве математической модели соответствующего процесса.
Дифференциальные уравнения играют важную роль в прикладной математике, физике и в других науках, таких как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений окружающего мира.
Теория численного решения дифференциальных уравнений хорошо разработана и на ее основе создано множество прикладных программ, позволяющих пользователю получить решение и вывести его в графическом виде. Среди этих программ следует в первую очередь отметить такие математические пакеты, как MATLAB, MATHEMATICA, MAPLE и MATHCAD. [3]
В представленной работе были использованы различные методы решения дифференциальных уравнений и их систем:
- Классический метод
- Операторный метод
- Решение ДУ с помощью рядов
- Метод Эйлера
- Метод Рунге-Кутты 4 порядка
Продемонстрированы возможности пакета MathCad, показаны расхождения решений разными методами.
В ходе проведения работы было выявлено, что наиболее точные решения получаются при использовании метода Рунге-Кутты 4 порядка и метода Эйлера. Наивысшей точностью обладает метод Рунге-Кутты 4 порядка точности.
Список использованных источников
- Казанцева Н. В. Численное решение задач высшей математики с использованием программных пакетов MathCad и MATLAB : метод. указания – Екатеринбург, УрГУПС, 2009 – 56 с.
- Шампайн Л. Ф., Гладвел И., Томпсон С. Решение обыкновенных дифференциальных уравнений с использованием MATLAB: Учебное пособие / Пер. с англ. И. А. Макарова. — СПб.: Издательство «Лань», 2011. — 304с: ил. — (Учебники для вузов. Специальная литература).
40
2
10.998
+
2
Z
2
2.746
1
Z
2
3.436
2
:=
127
0
U
:=
=
-
50.797i
3
10
1.098
+
)
(
-
5.499i
-
3.175
3
U
+
)
(
Z
+
Е = 100 В; f =50 Гц; C2 = 318 мкФ
L1 = 9.55 мГн; R1 = 4 Ом;
R2 = 40 Ом; R3 = 4 Ом.
0.338i
-
1.523
2
U
)
(
-
1.549i
1.239
1
U
1
P
Е = 100 В; f =50 Гц; C2 = 318 мкФ
L1 = 9.55 мГн; R1 = 4 Ом;
R2 = 40 Ом; R3 = 4 Ом.
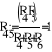

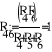
Iк1 (R1+R5+R5) -Iк2R2+Iк3R5=(E1-E2)-J*R2
-Iк1R2+Iк2 (R2+R4+R3) +I к3R4=(E2-E3)+J*R2
-Iк1 R5+Iк2 R4+Iк3 (R5+R4 +R6) =0
Gk=1/Rk
1(g1+g4+g5)- Ф2*g5-Ф3*g4=E2*g2
-1*g5+Ф2(g5+g6+g1)-Ф3*g6=E1*g1
-Ф1*g4-Ф2*g6+Ф3(g4+g6+g3)=E3*g3
I2-I4-I5=-J
I3+I4-I6=0
I5+I6+I1=0
I1R1-I5R5-I2R2=-E2
I2R2+I4R4-I3R3=E2-E3
-I4 R4-I6 R6+I5 R5=0
Е1 = 54 В; Е2 = 27 В; Е3 = 3 В; J =1,2 А
R1 = 8 Ом; R2 = 3 Ом; R3 = 1 Ом;
R4 = 4 Ом; R5 = 2 Ом; R6 = 45 Ом.
10
3.644х
Еm = 350 В; Т = 0,8·10 -2 с;
R1 = 14 Ом; R2 = 8 Ом;
R3 = 10 Ом;
L = 25 мГн; С = 60 мкФ
Е1 = 54 В; Е2 = 27 В; Е3 = 3 В; J =1,2 А
R1 = 8 Ом; R2 = 3 Ом; R3 = 1 Ом;
R4 = 4 Ом; R5 = 2 Ом; R6 = 45 Ом.
+
3
3
Еm = 350 В; Т = 0,8·10 -2 с;
R1 = 14 Ом; R2 = 8 Ом;
R3 = 10 Ом;
L = 25 мГн; С = 60 мкФ
575.647i
-
=
:=
г)
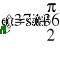
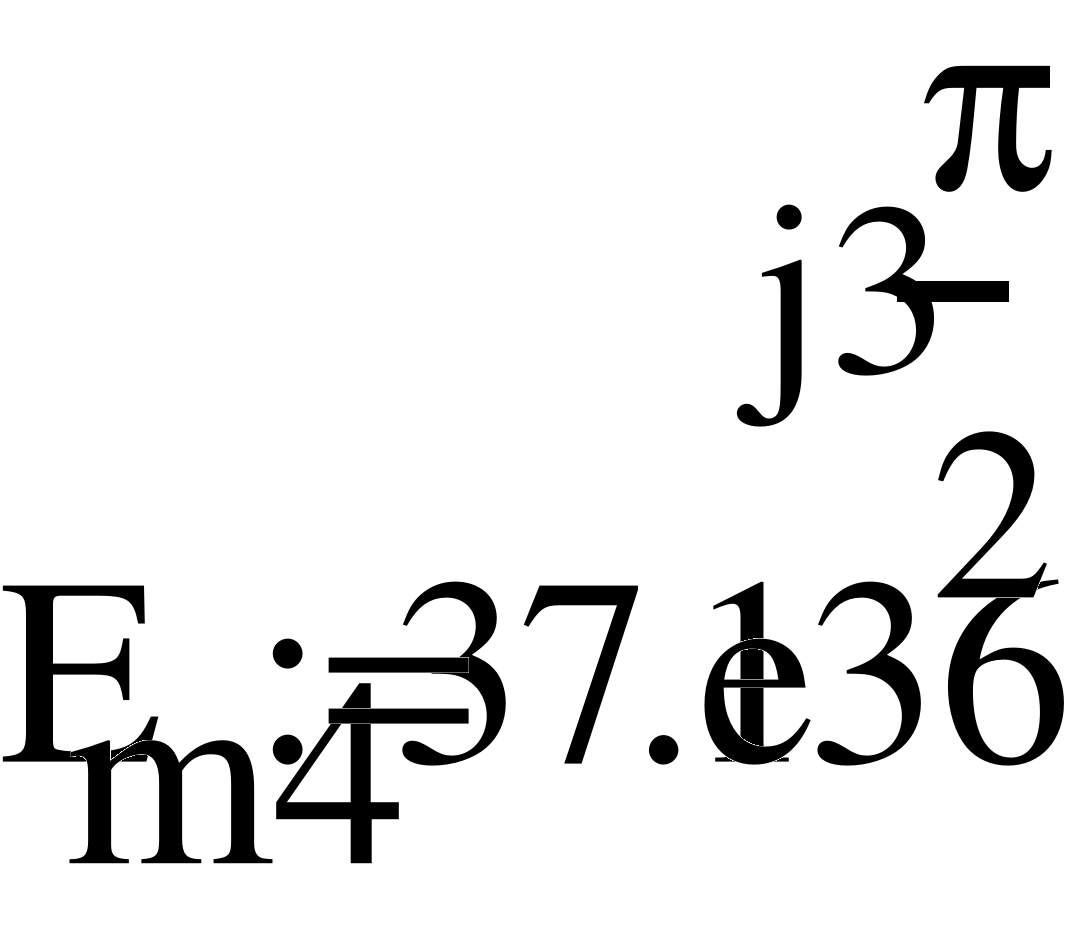
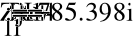
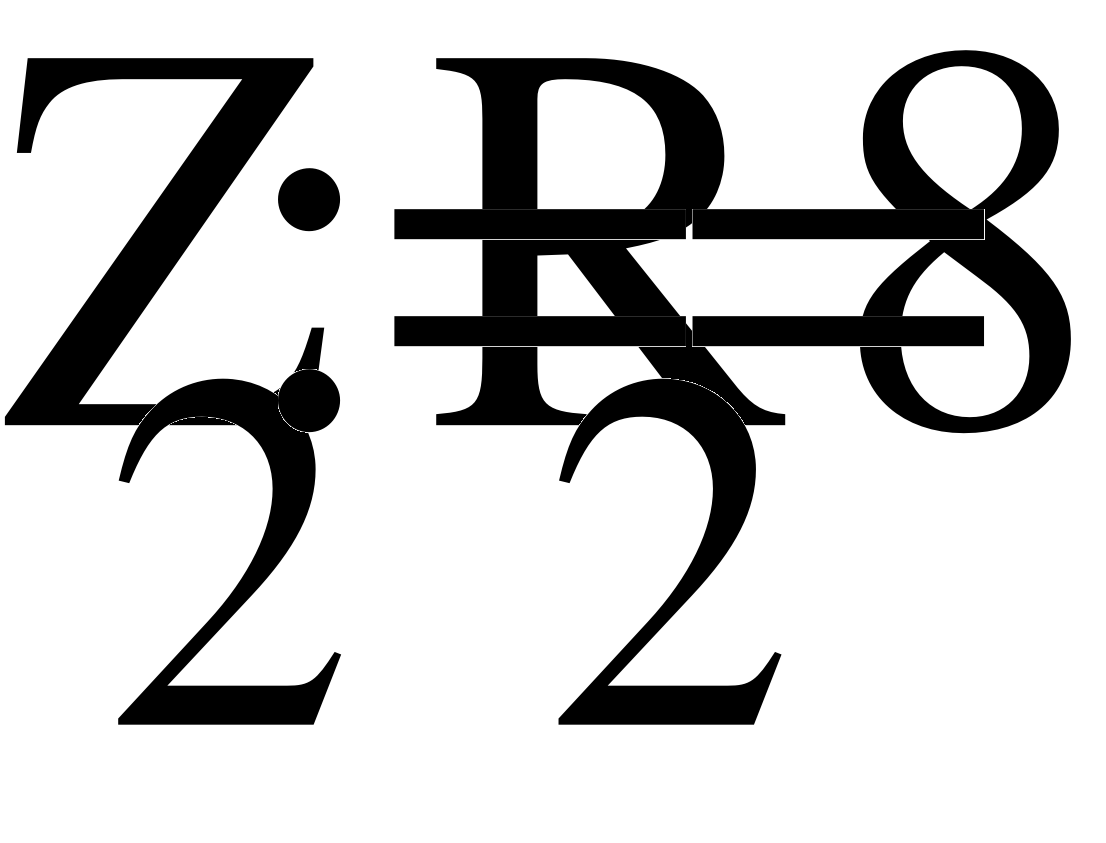
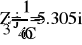
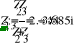
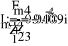
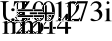
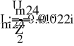
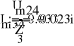

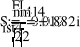
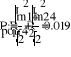
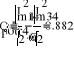
Задание на курсовую работу Анализ линейных электрических цепей в установившихся режимах