Регистры сдвига с линейной обратной связью как генераторы псевдослучайных чисел
Министерство образования и науки
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ СОЦИАЛЬНЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
КАФЕДРА ЗАЩИТЫ ИНФОРМАЦИИ
Криптографические методы и средства обеспечения информационной безопасности
Курсовая работа
«Регистры сдвига с линейной обратной связью как генераторы псевдослучайных чисел»
Выполнил:
студент 3-го курса
группа КЗОИ-Д-3
Ларионов И.П.
Проверила:
доц. Баранова Е.К.
Москва 2011
СОДЕРЖАНИЕ
Введение……………………………..…………………………………….3
- Теоретические основы работы…………………………………………4
- Общие сведения о регистрах сдвига с обратной связью……...…..4
- О потоковых шифрах на базе РгСсЛОС………………….………10
- О линейной сложности генерируемой псевдослучайной последовательности РгСсЛОС………………………………….……12
- О корреляционной независимости генерируемой последовательности псевдослучайных чисел РгСсЛОС………..….13
- О других способах вскрытия генерируемой последовательности псевдослучайных чисел РгСсЛОС…………………………………..14
- Программная реализация РгСсЛОС как генератора псевдослучайной последовательности….…………………………….15
- Обобщенная схема алгоритма…………………………………...15
- Описание программных модулей и интерфейса.……………….16
- Инструкция пользователя………………………………………...20
Заключение………………………………………………………………22
Список литературы………………………………………………….....23
Приложение А….………………………………………………………..24
ВВЕДЕНИЕ
Целью данной работы является разработка программного приложения, реализующего работу генератора псевдослучайных чисел на регистрах сдвига с обратной связью. Разработка данного приложения с графическим интерфейсом осуществляется на языке C++ для ОС Windows.
С развитием криптографии в ХХ веке перед криптографами встала задача создания шифровальных устройств и машин, которые могли бы быстро и надежно зашифровывать и расшифровывать сообщения. Этому требованию отвечали уже открытые в то время симметричные системы шифрования, однако их слабым местом была сильная зависимость от ключа и его секретность. Наиболее удобным классом шифров, которые можно было использовать для этой цели это шифры гаммирования. Возникла задача генерации гаммы, которую нельзя было бы обнаружить при дешифровании сообщения. Теоретически это было возможно, если каждый раз гамма была случайной и изменялась во времени. Однако при использовании абсолютно случайной изменяющейся гаммы было бы трудно обеспечить достоверную шифровку-дешифровку сообщения. Криптографы занялись решением этой задачи, целью которой было нахождения алгоритма реализующего генерацию случайной гаммы по определенному правилу, такая последовательность должна содержать в себе нули и единицы на «якобы» случайных позициях, причем число единиц и нулей должно быть примерно одинаково. Такая случайная последовательность была названа псевдослучайной, так как генерировалась она по определенному правилу, а не случайным образом.
Решение было вскоре найдено. Изучение свойств регистров сдвига позволило установить, что регистры сдвига с обратной связью способны генерировать достаточно стойкие к дешифровке псевдослучайные последовательности, обусловленные их внутренним строением.
1.Теоретические основы работы
1.1.Общие сведения о регистрах сдвига с линейной обратной связью
Последовательности регистров сдвига используются как в криптографии, так и в теории кодирования. Их теория прекрасно проработана, потоковые шифры на базе регистров сдвига являлись рабочей лошадкой военной криптографии задолго до появления электроники.
Регистр сдвига с обратной связью (далее РгСсОС) состоит из двух частей: регистра сдвига и функции обратной связи. Регистр сдвига представляет собой последовательность битов. Количество битов определяется длиной сдвигового регистра, если длина равна n битам, то регистр называется n-битовым сдвиговым регистром. Всякий раз, когда нужно извлечь бит, все биты сдвигового регистра сдвигаются вправо на 1 позицию. Новый крайний левый бит является функцией всех остальных битов регистра. На выходе сдвигового регистра оказывается один, обычно младший значащий, бит. Периодом сдвигового регистра называется длина получаемой последовательности до начала ее повторения.
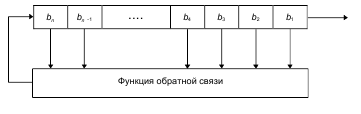
Рисунок Регистр сдвига с обратной связью
Регистры сдвига очень быстро нашли применение в потоковых шифрах, так как они легко реализовывались с помощью цифровой аппаратуры. В 1965 году Эрнст Селмер (Ernst Selmer), главный криптограф норвежского правительства, разработал теорию последовательности регистров сдвига [3]. Соломон Голомб (Solomon Golomb), математик NSA, написал книгу, излагающие некоторые свои результаты и результаты Селмера [7]. Простейшим видом регистра сдвига с обратной связью является регистр сдвига с линейной обратной связью (linear feedback shift register, далее LFSR или РгСсЛОС). Обратная связь таких регистров представляет собой просто XOR (сложение по модулю два) некоторых битов регистра, перечень этих битов называется отводной последовательностью (tap sequence). Иногда такой регистр называется конфигурацией Фиббоначи. Из-за простоты последовательности обратной связи для анализа РгСсЛОС можно использовать довольно развитую математическую теорию. Проанализировав получаемые выходные последовательности, можно убедиться в том, что эти последовательности достаточно случайны, чтобы быть безопасными. РгСсЛОС чаще других сдвиговых регистров используются в криптографии.
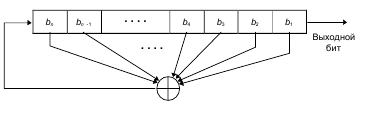
Рисунок РгСсЛОС Фиббоначи
В общем случае n-битовый РгСсЛОС может находиться в одном из N=2n-1 внутренних состояний. Это означает, что теоретически такой регистр может генерировать псевдослучайную последовательность с периодом Т=2n-1 битов. (Число внутренних состояний и период равны N=Tmax=2n-1, потому что заполнение РгСсЛОС нулями, приведет к тому, что сдвиговый регистр будет выдавать бесконечную последовательность нулей, что абсолютно бесполезно). Только при определенных отводных последовательностях РгСсЛОС циклически пройдет через все 2n-1 внутренних состояний, такие РгСсЛОС являются РгСсЛОС с максимальным периодом. Получившийся результат называется М-последовательностью.
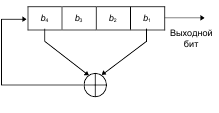
Пример. На рисунке ниже показан 4-битовый РгСсЛОС с отводом от первого и четвертого битов. Если его проинициализировать значением 1111, то до повторения регистр будет принимать следующие внутренние состояния:
|
Номер такта сдвига (внутреннего состояния)
|
Состояние регистров
|
Выходной бит
|
|
|
T1
|
T2
|
T3
|
T4
|
|
|
Инициальное значение
|
1
|
1
|
1
|
1
|
-
|
|
1
|
0
|
1
|
1
|
1
|
1
|
|
2
|
1
|
0
|
1
|
1
|
1
|
|
3
|
0
|
1
|
0
|
1
|
1
|
|
4
|
1
|
0
|
1
|
0
|
0
|
|
5
|
1
|
1
|
0
|
1
|
1
|
|
6
|
0
|
1
|
1
|
0
|
0
|
|
7
|
0
|
0
|
1
|
1
|
1
|
|
8
|
1
|
0
|
0
|
1
|
1
|
|
9
|
0
|
1
|
0
|
0
|
0
|
|
10
|
0
|
0
|
1
|
0
|
0
|
|
11
|
0
|
0
|
0
|
1
|
1
|
|
12
|
1
|
0
|
0
|
0
|
0
|
|
13
|
1
|
1
|
0
|
0
|
0
|
|
14
|
1
|
1
|
1
|
0
|
0
|
|
15 (возврат в инициальное состояние)
|
1
|
1
|
1
|
1
|
1
|
|
16 (повтор состояний)
|
0
|
1
|
1
|
1
|
1
|
Выходной последовательностью будет строка младших значащих битов: 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0 с периодом Т=15, общее число возможных внутренних состояний (кроме нулевого), N=24-1=16-1=15=Tmax, следовательно, выходная последовательность – M-последовательность.
Для того чтобы конкретный РгСсЛОС имел максимальный период, многочлен, образованный из отводной последовательности и константы 1, должен быть примитивным по модулю 2. Многочлен представляется в виде суммы степеней, например многочлен степени n представляется так:
anxn+an-1xn-1+…+a1x1+a0x0=anxn+an-1xn-1+…+a1x+a0, где аi={0,1} для i=1…n, a xi – указывает разряд.
Степень многочлена является длиной сдвигового регистра. Примитивный многочлен степени n - это неприводимый многочлен, который является делителем x2n1+1, но не является делителем xd+1 для всех d, являющихся делителями 2n-1. Соответствующую математическую теорию можно найти в [4].
В общем случае не существует простого способа генерировать примитивные многочлены данной степени по модулю 2. Проще всего выбирать многочлен случайным образом и проверять, не является ли он примитивным. Это нелегко и чем-то похоже на проверку, не является ли простым случайно выбранное число - но многие математические пакеты программ умеют решать такую задачу.
Некоторые, но, конечно же, не все, многочлены различных степеней, примитивные по модулю 2, приведены далее. Например, запись
(32, 7, 5, 3, 2, 1, 0) означает, что следующий многочлен примитивен по модулю 2: x32 + x7 +x5 + x3 + x2 + x + 1.
Это можно легко обобщить для РгСсЛОС с максимальным периодом. Первым числом является длина РгСсЛОС. Последнее число всегда равно 0, и его можно опустить. Все числа, за исключением 0, задают отводную последовательность, отсчитываемую от левого края сдвигового регистра. То есть, члены многочлена с меньшей степенью соответствуют позициям ближе к правому краю регистра.
Продолжая пример, запись (32, 7, 5, 3, 2, 1, 0) означает, что для взятого 32-битового сдвигового регистра новый бит новый бит генерируется с помощью XOR тридцать второго, седьмого, пятого, третьего, второго и первого битов, получающийся РгСсЛОС будет иметь максимальную длину, циклически проходя до повторения через 232-1 значений.
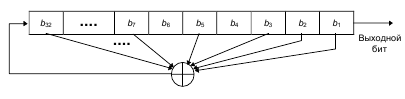
Рисунок 4 32-битовый РгСсЛОС с максимальной длиной
Рассмотрим программный код РгСсЛОС, у которого отводная последовательность характеризуется многочленом (32, 7, 5, 3, 2, 1, 0). На языке C выглядит следующим образом [1]:
int LFSR ( ) {
static unsigned long ShiftRegister = 1;
/* Все, кроме 0. */
ShiftRegister = ((((ShiftRegister >> 31)
^(ShiftRegister >> 6)
^(ShiftRegister >> 4)
^(ShiftRegister >> 2)
^(ShiftRegister >> 1)
^ShiftRegister))
& 0x00000001)
<<31)
| (ShiftRegister >> 1) ;
return ShiftRegister & 0x00000001;}
Если сдвиговый регистр длиннее компьютерного слова, код усложняется, но не намного. В приложении B приведена таблица некоторых примитивных многочленов по модулю 2 [1], будем использовать ее в дальнейшем для выявления некоторых свойств этих многочленов, а также в программной реализации для задания отводной последовательности.
Следует обратить внимание, что у всех элементов таблицы нечетное число коэффициентов. Такая длинная таблица приведена для дальнейшей работы с РгСсЛОС, так как РгСсЛОС часто используются для криптографии с потоковыми шифрами и в генераторах псевдослучайных чисел. В нашем случае можно использовать многочлены со старшей степенью не более семи.
Если p(x) примитивен, то примитивен и xnp(1/x), поэтому каждый элемент таблицы на самом деле определяет два примитивных многочлена. Например, если (a, b, 0) примитивен, то примитивен и (a, a-b, 0). Если примитивен (a, b, c, d, 0), то примитивен и (a, a-d, a-c, a-b, 0). Математически:
если примитивен xa +xb+1, то примитивен и xa+xa-b+1,
если примитивен xa+xb+xc+xd+1, то примитивен и xa+xa-d+xa-c+xa-b+1. [1,2] Быстрее всего программно реализуются примитивные трехчлены, так как для генерации нового бита нужно выполнять XOR только двух битов сдвигового регистра (нулевой член не учитывается, т.е. х0=1, см. пример выше). Действительно, все многочлены обратной связи, приведенные в таблице, являются разреженными, то есть, у них немного коэффициентов. Разреженность всегда представляет собой источник слабости, которой иногда достаточно для вскрытия алгоритма. Для криптографических алгоритмов гораздо лучше использовать плотные примитивные многочлены, те, у которых много коэффициентов. Применяя плотные многочлены, особенно в качестве части ключа, можно использовать значительно более короткие РгСсЛОС.
Генерировать плотные примитивные многочлены по модулю 2 нелегко. В общем случае для генерации примитивных многочленов степени k нужно знать разложение на множители числа 2k-1.
Сами по себе РгСсЛОС являются хорошими генераторами псевдослучайных последовательностей, но они обладают некоторыми нежелательными неслучайными (детерминированными) свойствами. Последовательные биты линейны, что делает их бесполезными для шифрования. Для РгСсЛОС длины n внутреннее состояние представляет собой предыдущие n выходных битов генератора. Даже если схема обратной связи хранится в секрете, она может быть определена по 2n выходным битам генератора с помощью высоко эффективного алгоритма Berlekamp-Massey [5].
Кроме того, большие случайные числа, генерируемые с использованием идущих подряд битов этой последовательности, сильно коррелированны и для некоторых типов приложений вовсе не являются случайными. Несмотря на это РгСсЛОС часто используются для создания алгоритмов шифрования в качестве составных частей систем и алгоритмов шифрования.
1.2.О потоковых шифрах на базе РгСсЛОС
Основной подход при проектировании генератора потока ключей на базе РгСсЛОС прост. Сначала берется один или несколько РгСсЛОС, обычно с различными длинами и различными многочленами обратной связи. (Если длины взаимно просты, а все многочлены обратной связи примитивны, то у образованного генератора будет максимальная длина.) Ключ является начальным состоянием регистров РгСсЛОС. Каждый раз, когда необходим новый бит, сдвиньте на бит регистры РгСсЛОС (это иногда называют тактированием (clocking)). Бит выхода представляет собой функцию, желательно нелинейную, некоторых битов регистров РгСсЛОС. Эта функция называется комбинирующей функцией, а генератор в целом - комбинационным генератором. (Если бит выхода является функцией единственного РгСсЛОС, то генератор называется фильтрующим генератором.) Большая часть теории подобного рода устройств разработана Селмером (Selmer) и Нилом Цирлером (Neal Zierler). Можно ввести ряд усложнений. В некоторых генераторах для различных РгСсЛОС используется различная тактовая частота, иногда частота одного генератора зависит от выхода другого. Все это электронные версии идей шифровальных машин, появившихся до Второй мировой войны, которые называются генераторами с управлением тактовой частотой (clock-controlled generators). Управление тактовой частотой может быть с прямой связью, когда выход одного РгСсЛОС управляет тактовой частотой другого РгСсЛОС, или с обратной связью, когда выход одного РгСсЛОС управляет его собственной тактовой частотой. Хотя все эти генераторы чувствительны, по крайней мере теоретически, к вскрытиям вложением и вероятной корреляцией, многие из них безопасны до сих пор.
Ян Касселлс (Ian Cassells), ранее возглавлявший кафедру чистой математики в Кембридже и работавший криптоаналитиком в Блетчли Парк (Bletchly Park), сказал, что «криптография - это смесь математики и путаницы, и без путаницы математика может быть использована против вас». Он имел в виду, что в потоковых шифрах для обеспечения максимальной длины и других свойств необходимы определенные математические структуры, такие как РгСсЛОС, но, чтобы помешать кому-то получить содержание регистра и вскрыть алгоритм, необходимо внести некоторый сложный нелинейный беспорядок. Этот совет справедлив и для блочных алгоритмов.
Большинство реальных потоковых шифров основаны на РгСсЛОС. Даже в первые дни электроники построить их было несложно. Сдвиговый регистр не представляет собой ничего большего, чем массив битов, а последовательность обратной связи - набор вентилей XOR. Даже при использовании СБИС потоковый шифр на базе РгСсЛОС обеспечивает немалую безопасность с помощью нескольких логических вентилей. Проблема РгСсЛОС состоит в том, что их программная реализация очень неэффективна. Вам приходится избегать разреженных многочленов обратной связи - они облегчают корреляционные вскрытия – а плотные многочлены обратной связи неэффективны.
Эта отрасль криптографии быстро развивается и находится под зорким государственным контролем со стороны NSA. Большинство разработок засекречены - множество используемых сегодня военных систем шифрования основаны на РгСсЛОС. Действительно, у большинства компьютеров Cray (Cray 1, Cray X-MP, Cray Y-MP) есть весьма любопытная инструкция, обычно называемая как "счетчик совокупности" (population count). Она подсчитывает количество единиц в регистре и может быть использована как для эффективного вычисления расстояния Хэмминга между двумя двоичными словами и для реализации векторизированной версии РгСсЛОС. Эта инструкция считается канонической инструкцией NSA, обязательно фигурирующей почти во всех контрактах, касающихся компьютеров.
С другой стороны было взломано удивительно большое число казавшихся сложными генераторов на базе сдвиговых регистров. И, конечно же, число таких генераторов, взломанных военными криптоаналитическими учреждениями, такими как NSA, еще больше.
1.3.О линейной сложности генерируемой последовательности псевдослучайных чисел РгСсЛОС
Анализировать потоковые шифры часто проще, чем блочные. Например, важным параметром, используемым для анализа генераторов на базе РгСсЛОС, является линейная сложность (linear complexity), или линейный интервал. Она определяется как длина n самого короткого РгСсЛОС, который может имитировать выход генератора. Любая последовательность, генерированная конечным автоматом над конечным полем, имеет конечную линейную сложность [6]. Линейная сложность важна, потому что с помощью простого алгоритма, называемого алгоритмом Berlekamp-Massey, можно определить этот РгСсЛОС, проверив только 2n битов потока ключей [6]. Воссоздавая нужный РгСсЛОС, вы взламываете потоковый шифр.
Эта идею можно расширить с полей на кольца и на случаи, когда выходная последовательность рассматривается как числа в поле нечетной характеристики. Дальнейшее расширение приводит к вводу понятия профиля линейной сложности, который определяет линейную сложность последовательности по мере ее удлинения. Существую также понятия сферической и квадратичной сложности. В любом случае следует помнить, что высокая линейная сложность не обязательно гарантирует безопасность генератора, но низкая линейная сложность указывает на недостаточную безопасность генератора.
1.4.О корреляционной независимости генерируемой последовательности псевдослучайных чисел РгСсЛОС
Криптографы пытаются получить высокую линейную сложность, нелинейно объединяя результаты некоторых выходных последовательностей. При этом опасность состоит в том, что одна или несколько внутренних выходных последовательностей - часто просто выходы отдельных РгСсЛОС - могут быть связаны общим ключевым потоком и вскрыты при помощи линейной алгебры. Часто такое вскрытие называют корреляционным вскрытием или вскрытием разделяй-и-властвуй. Томас Сигенталер (Thomas Siegenthaler) показал, что можно точно определить корреляционную независимость, и что существует компромисс между корреляционной независимостью и линейной сложностью [5].
Основной идеей корреляционного вскрытия является обнаружение некоторой корреляции между выходом генератора и выходом одной из его составных частей. Тогда, наблюдая выходную последовательность, можно получить информацию об этом промежуточном выходе. Используя эту информацию и другие корреляции, можно собирать данные о других промежуточных выходах до тех пор, пока генератор не будет взломан.
Против многих генераторов потоков ключей на базе РгСсЛОС успешно использовались корреляционные вскрытия и их вариации, такие как быстрые корреляционные вскрытия, предлагающие компромисс между вычислительной сложностью и эффективностью.
1.5.О других способах вскрытия генерируемой последовательности псевдослучайных чисел РгСсЛОС
Существуют и другие способы вскрытия генераторов потоков ключей. Тест на линейную корректность (linear consistency) пытается найти некоторое подмножество ключа шифрования с помощью матричной техники. Существует и вскрытие корректности "встречей посередине" (meet-in-the-middle consistency attack). Алгоритм линейного синдрома (linear syndrome algorithm) основан на возможности записать фрагмент выходной последовательности в виде линейного уравнения. Существует вскрытие лучшим аффинным приближением (best afflne approximation attack) и вскрытие выведенным предложением (derived sequence attack). К потоковым шифрам можно применить также методы дифференциального и линейного криптоанализа.
2. Описание программной реализации РгСсЛОС как генератора псевдослучайной последовательности
2.1.Обобщенная схема алгоритма
2.2.Описание программных модулей и интерфейса
Ниже на рисунке 3 представлено окно программы. 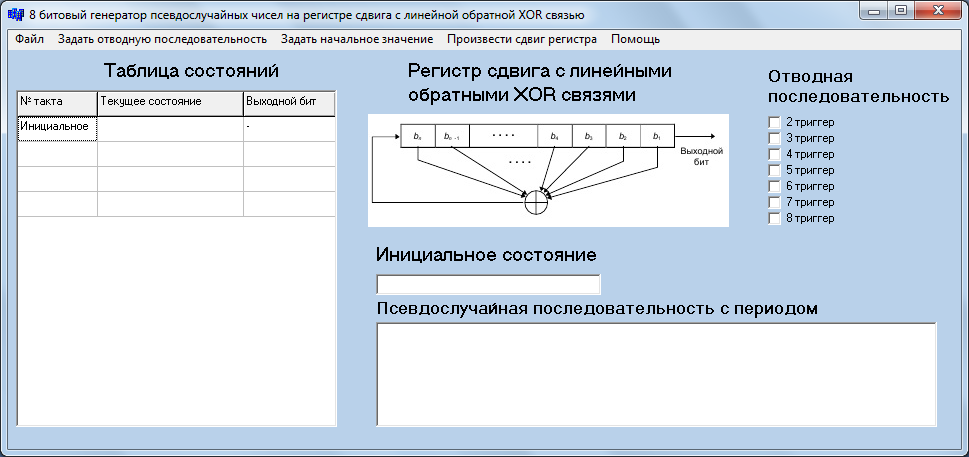
Рисунок Интерфейс программы
В меню есть следующие функции:
Эта функция осуществляет создание файла отчета, куда записывается инициальное состояние РгСсЛОС, отводная последовательность, период полученной псевдослучайной последовательности бит, сама последовательность и таблица состояний. Если файл успешно был сохранен, то выдается сообщение об успешном сохранении (рисунок 4). Рекомендуемое расширение файла отчета *.txt.
Рисунок
Эта функция обеспечивает закрытие приложения.
- Задать отводную последовательность
Эта функция формирует отводную последовательность, считывая значения из клеточек, которые пользователь отметил галочкой на экранной форме. После чего она уведомляет пользователя о создании отводной последовательности (рисунок 5). Отводная последовательность определяет от каких триггеров регистра сдвига будут идти обратные связи XOR для формирования бита смещения. По умолчанию обратная связь от первого триггера стоит всегда, при отсутствии других связей, будет осуществляться сдвиг влево с перестановкой младшего бита на позицию старшего.
Рисунок
- Установить инициальное значение
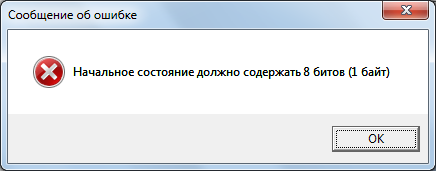
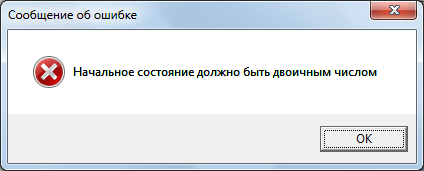
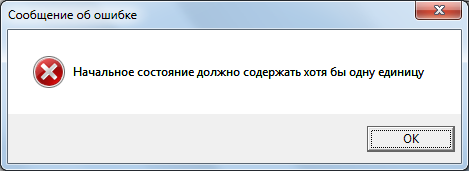
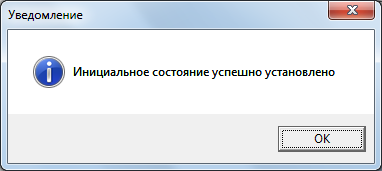
Эта функция считывает введенное пользователем инициальное значение регистра из окна Edit1 и осуществляет проверку введенного значения согласно заданным условиям: введенная строка непустая (рисунок 6), введенная строка имеет длину равную восьми (8бит=1байт, рисунок 7), введенная строка содержит только нули и/или единицы (рисунок 8), введенная строка ненулевая (рисунок 9). В противном случае выдаются сообщения об ошибке, пользователь должен их исправить и снова нажать на кнопку. В случае успешной проверки инициальное значение будет записано в таблицу состояний в строке «Инициальное» и выдано уведомление (рисунок 10).
Рисунок
Рисунок
Рисунок
Рисунок
Рисунок
- Произвести сдвиг регистра
Эта функция эмулирует работу регистра сдвига. Последовательно производя 256 сдвигов, каждый сдвиг формирует выходной бит псевдослучайной последовательности и новое состояние регистра. Как только находится состояние регистра равное инициальному, вычисляется период и выводит в поле Memo1 полученную псевдослучайную последовательность.
Эта функция выводит на экран краткое описание программы и инструкцию (рисунок 11).
Рисунок
Эта функция выводит на экран информацию об авторе программы (рисунок 12).
Рисунок
2.3.Инструкция пользователя
- Сначала установите инициальное состояние регистра. Оно должно содержать восемь двоичных символов. В противном случае будет выдано сообщение об ошибке и Вам придется исправить введенное значение. Нажмите пункт меню «Задать инициальное значение».
- Затем отметьте флажками в клеточках обратные связи регистра (Отводная последовательность). Нажмите пункт меню «Задать отводную последовательность».
- Далее нажмите пункт меню «Сдвиг регистра». Обязательно перед этим удостоверьтесь в том, что вы выполнили пункт 1 и 2, иначе произойдет программная ошибка.
- Получив результаты вы можете их сохранить нажав пункт меню «Файл->Сохранить отчет». Обязательно перед этим удостоверьтесь в том, что вы выполнили пункты 1-3, иначе произойдет программная ошибка.
- Для получения справки нажмите пункты меню «Файл->О программе», «Файл->Об авторе».
- Чтобы посмотреть работу регистра при других значениях отводной последовательности и инициального состояния регистра, повторите последовательно действия в пунктах 1-3, введя другие параметры.
ЗАКЛЮЧЕНИЕ
В данной работе были рассмотрены РгСсЛОС в качестве генераторов псевдослучайных чисел. Программа может служить наглядной демонстрацией принципов работы регистров сдвига с линейной обратной связью по XOR. На ней можно изучать принцип формирования псевдослучайной последовательности битов, зависимость между инициальным значением регистра и значением псевдослучайной последовательности, отводной последовательностью и периодом. Получаемую псевдослучайную гамму можно использовать в другом программном приложении (например, программная реализация шифра гаммирования).
На сегодняшний момент данные регистры не используются как самостоятельные генераторы псевдослучайных чисел, а входят в состав более сложных устройств. Однако именно они открыли новые направления в математике (поиск примитивных многочленов в конечных полях, математические способы взлома генераторов псевдослучайных чисел). Без знания принципов работы генераторов на РгСсЛОС нельзя понять работу более сложных устройств. Благодаря своей простой аппаратной реализации они получили широкое распространение в технике. Исследование РгСсОС привело к возникновению новых шифров - блочных и потоковых - основанных на этих типах регистров (шифр скользящей перестановки, DES и т.п.; ЭЦП, хеш-функции).
В целом исследования в этой области серьезно подтолкнули развитие криптографии и криптоаналитики, ЭВМ и устройств, а также позволили реализовать и ряд других полезных функций (например, корректирующие цикловые коды).
СПИСОК ЛИТЕРАТУРЫ
- Шнайер Брюс. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си. – М.: Триумф, 2002
- Бабаш А.В. Криптографические и теоретико-автоматные аспекты современной защиты информации. Том 1 – М.: Изд. центр ЕАОИ, 2009. – 414 с.
- Е.С. Селмер. Монография: «Линейная рекурсия в конечном поле». Университет Бергена, Норвегия, 1966.
- Н.Зиерлер и Дж. Бриллхарт. "О примитивных трехчленах по модулю 2", журнал Информация и Контроль, издание 13 №6 декабрь 1968, стр. 541-544.
- К.Х. Мейер и У.Л.Тучман. "Псевдослучайные коды могут быть взломаны, " журнал Электроник Дизайн, №. 23, ноябрь 1972.
- Дж.Л.Массей. "Обобщение регистров сдвига и дешифровка кода Бозе-Чоудхури-Хоквингема", IEEE Transactions on Information Theory, v. IT-15, n. 1, январь 1969, стр. 122-127.
- С.У. Голомб. Последовательности регистров сдвига, Сан-Франциско, Голден-Дей, 1967 (переиздано Аигеан Парк Пресс, 1982).
Приложение А
Таблица некоторых примитивных многочленов по модулю 2
(1, 0)
(2, 1, 0)
(3, 1, 0)
(4, 1, 0)
(5, 2, 0)
(6, 1, 0)
(7, 1, 0)
(7, 3, 0)
(8, 4, 3, 2, 0)
(9, 4, 0)
(10, 3, 0)
(11, 2, 0)
(12, 6, 4, 1, 0)
(13, 4, 3, 1, 0)
(14, 5, 3, 1, 0)
(15, 1, 0)
(16, 5, 3.2, 0)
(17, 3, 0)
(17, 5, 0)
(17, 6, 0)
(18, 7, 0)
(18, 5, 2, 1, 0)
(19, 5, 2, 1, 0)
(20, 3, 0)
(21, 2, 0)
(22, 1, 0)
(23, 5, 0)
(24, 4, 3, 1, 0)
(25, 3, 0)
(26, 6, 2, 1, 0)
(27, 5, 2, 1, 0)
(28, 3, 0)
(29, 2, 0)
(30, 6, 4, 1.0)
(31, 3, 0)
(31, 6, 0)
(31, 7, 0)
(31, 13, 0)
(32, 7, 6, 2, 0)
(32, 7, 5, 3, 2, 1, 0)
(33, 13, 0)
(33, 16, 4, 1, 0)
(34, 8, 4, 3, 0)
(34, 7, 6, 5, 2, 1, 0)
(35, 2, 0)
(135, 11, 0)
(135, 16, 0)
(135, 22, 0)
(136, 8, 3, 2, 0)
(137, 21, 0)
(138, 8, 7, 1, 0)
(139, 8, 5, 3, 0)
(140, 29, 0)
(141, 13, 6, 1, 0)
(142, 21, 0)
(143, 5, 3, 2, 0)
(144, 7, 4, 2, 0)
(145, 52, 0)
(145, 69, 0)
(146, 5, 3, 2, 0)
(147, 11, 4, 2, 0)
(148, 27, 0)
(149, 10, 9, 7, 0)
(150, 53, 0)
(151, 3, 0)
(151, 9, 0)
(151, 15, 0)
(151, 31, 0)
(151, 39, 0)
(151, 43, 0)
(151, 46, 0)
(151, 51, 0)
(151, 63, 0)
(151, 66, 0)
(151, 67, 0)
(151, 70, 0)
(36, 11, 0)
(36, 6, 5, 4, 2, 1, 0)
(37, 6, 4, 1, 0)
(37, 5, 4, 3, 2, 1, 0)
(38, 6, 5, 1, 0)
(39, 4, 0)
(40, 5, 4, 3, 0)
(41, 3, 0)
(42, 7, 4, 3, 0)
(42, 5, 4, 3, 2, 1, 0)
(43, 6, 4, 3, 0)
(44, 6, 5, 2, 0)
(45, 4, 3, 1, 0)
(46, 8, 7, 6, 0)
(46, 8, 5, 3, 2, 1, 0)
(47, 5, 0)
(48, 9, 7, 4, 0)
(48, 7, 5, 4, 2, 1, 0)
(49, 9, 0)
(49, 6, 5, 4, 0)
(50, 4, 3, 2, 0)
(51, 6, 3, 1, 0)
(52, 3, 0)
(53, 6, 2, 1, 0)
(54, 8, 6, 3, 0)
(54, 6, 5, 4, 3, 2, 0)
(55, 24, 0)
(55, 6, 2, 1, 0)
(56, 7, 4, 2, 0)
(57, 7, 0)
(57, 5, 3, 2, 0)
(58, 19.0)
(58, 6, 5, 1, 0)
(59, 7, 4, 2, 0)
(59, 6, 5, 4, 3, 1, 0)
(60, 1, 0)
(61, 5, 2, 1, 0)
(62, 6, 5, 3, 0)
(63, 1, 0)
(64, 4, 3, 1, 0)
(65, 18, 0)
(65, 4, 3, 1, 0)
(66, 9, 8, 6, 0)
(66, 8, 6, 5, 3, 2, 0)
(67, 5, 2, 1, 0)
(152, 6, 3, 2, 0)
(153, 1, 0)
(153, 8, 0)
(154, 9, 5, 1, 0)
(155, 7, 5, 4, 0)
(156, 9, 5, 3, 0)
(157, 6, 5, 2, 0)
(158, 8, 6, 5, 0)
(159, 31, 0)
(159, 34, 0)
(159, 40, 0)
(160, 5, 3, 2, 0)
(161, 18, 0)
(161, 39, 0)
(161, 60, 0)
(162, 8, 7, 4, 0)
(163, 7, 6, 3, 0)
(164, 12, 6, 5, 0)
(165, 9, 8, 3, 0)
(166, 10, 3, 2, 0)
(167, 6, 0)
(170, 23, 0)
(172, 2, 0)
(174, 13, 0)
(175, 6, 0)
(175, 16, 0)
(175, 18, 0)
(175, 57, 0)
(177, 8, 0)
(177, 22, 0)
(1 77, 88, 0)
(68, 9, 0)
(68, 7, 5, 1, 0)
(69, 6, 5, 2, 0)
(70, 5, 3, 1, 0)
(71, 6, 0)
(71, 5, 3, 1, 0)
(72, 10, 9, 3, 0)
(72, 6, 4, 3, 2, 1, 0)
(73, 25, 0)
(73, 4, 3, 2, 0)
(74, 7, 4, 3, 0)
(75, 6, 3, 1, 0)
(76, 5, 4, 2, 0)
(77, 6, 5, 2, 0)
(78, 7, 2, 1, 0)
(79, 9, 0)
(79, 4, 3, 2, 0)
(80, 9, 4, 2, 0)
(80, 7, 5, 3, 2, 1, 0)
(81, 4, 0)
(82, 9, 6, 4, 0)
(82, 8, 7, 6, 1, 0)
(83, 7, 4, 2, 0)
(84, 13, 0)
(84, 8, 7, 5, 3, 1, 0)
(85, 8, 2, 1, 0)
(86, 6, 5, 2, 0)
(87, 13, 0)
(87, 7, 5, 1, 0)
(88, 11, 9, 8, 0)
(88, 8, 5, 4, 3, 1, 0)
(89, 38, 0)
(89, 51, 0)
(89, 6, 5, 3, 0)
(90, 5, 3, 2, 0)
(91, 8, 5, 1, 0)
(91, 7, 6, 5, 3, 2, 0)
(92, 6, 5, 2, 0)
(93, 2, 0)
(94, 21, 0)
(94, 6, 5, 1, 0)
(95, 11, 0)
(95, 6, 5, 4, 2, 1, 0)
(96, 10, 9, 6, 0)
(96, 7, 6, 4, 3, 2, 0)
(178, 87, 0)
(183, 56, 0)
(194, 87, 0)
(198, 65, 0)
(201, 14, 0)
(201, 17, 0)
(201, 59, 0)
(201, 79, 0)
(202, 55, 0)
(207, 43, 0)
(212, 105, 0)
(218, 11, 0)
(218, 15, 0)
(218, 71, 0)
(218.83, 0)
(225, 32, 0)
(225, 74, 0)
(225, 88, 0)
(225, 97, 0)
(225, 109, 0)
(231, 26, 0)
(231, 34, 0)
(234, 31, 0)
(234, 103, 0)
(236, 5, 0)
(250, 103, 0)
(255, 52, 0)
(255, 56, 0)
(255, 82, 0)
(258, 83, 0)
(266, 47, 0)
(97, 6, 0)
(98, 11, 0)
(98, 7, 4, 3, 1, 0)
(99, 7, 5, 4, 0)
(100, 37, 0)
(100, 8, 7, 2, 0)
(101, 7, 6, 1, 0)
(102, 6, 5, 3, 0)
(103, 9, 9)
(104, 11, 10, 1, 0)
(105, 16, 0)
(106, 15, 0)
(107, 9, 7, 4, 0)
(108, 31, 0)
(109, 5, 4, 2.0)
(110, 6, 4, 1, 0)
(111, 10, 0)
(111, 49, 0)
(113, 9, 0)
(113, 15, 0)
(113, 30, 0)
(114, 11, 2, 1, 0)
(115, 8, 7, 5, 0)
(116, 6, 5, 2, 0)
(117, 5, 2, 1, 0)
(118, 33, 0)
(119, 8, 0)
(119, 45, 0)
(120, 9, 6, 2, 0)
(121, 18, 0)
(122, 6, 2, 1, 0)
(123, 2, 0)
(124, 37, 0)
(125, 7, 6, 5, 0)
(126, 7, 4, 2, 0)
(127, 1, 0)
(127, 7, 0)
(127, 63, 0)
(128, 7, 2, 1, 0)
(129, 5, 0)
(130, 3, 0)
(131, 8, 3, 2, 0)
(132, 29, 0)
(133, 9, 8, 2, 0)
(134, 57, 0)
(270, 133, 0)
(282, 35, 0)
(282, 43, 0)
(286, 69, 0)
(286, 73, 0)
(294, 61, 0)
(322, 67, 0)
(333, 2, 0)
(350, 53, 0)
(366, 29, 0)
(378, 43, 0)
(378, 107, 0)
(390, 89, 0)
(462, 73, 0)
(521, 32, 0)
(521, 48, 0)
(521, 158, 0)
(521, 168, 0)
(607, 105, 0)
(607, 147, 0)
(607, 273, 0)
(1279, 216, 0)
(1279, 418, 0)
(2281, 715, 0)
(2281, 915, 0)
(2281, 1029, 0)
(3217, 67, 0)
(3217, 576, 0)
(4423, 271, 0)
(9689, 84, 0)
Ввод инициального состояния (ИС)
роверка на правильность ввода
Выдача сообщения об ошибке
Установка отводной последовательности
Запись ИС в таблицу состояний
Запись i-го состояния регистра и выходного бита в таблицу состояний
ИС==Текущее состояние
Сохранение результатов
Вывод псевдослучайно последовательности
Выход
Запуск
Да
Да
Нет
Нет
Регистры сдвига с линейной обратной связью как генераторы псевдослучайных чисел