Исследование психологических особенностей студентов вуза статистическими методами

ОГЛАВЛЕНИЕ

Введение……………………………………………………………………..……….3Глава 1. Статистические методы в психологии……………………….….............7

Глава 2. Исследование психологических особенностей студентов вуза статистическими методами……………………………...………………..….........16

Заключение……………………………………………………….……………...…28

Список литературы………………………………………………….………….....29

ВВЕДЕНИЕ

Актуальность работы. Впервые термин «математическая или статистическая психология» был предложен И. Гербартом в 1822 г., позже его ученик М. Дробиш написал книгу «Первоосновы учения о математической психологии». Однако дальнейшее развитие статистическая психология получила лишь в 1963 г. уже в США, где появился учебник по математической психологии. Там же была организована первая лаборатория по математической психологии, и стал издаваться журнал «Математическая психология», который является единственным и в настоящее время. [1]

В России математическая психология начала развиваться в семидесятых годах XX в., и одним из ее основателей был В.Ю. Крылов. Применение статистических методов в психологии началось практически с момента выделения психологии как экспериментальной дисциплины. Применение математических моделей уже на ранних этапах становления психологии неслучайно и является следствием общей тенденции математизации наук. [8]

Первая стадия характеризовалась применением статистических методов анализа результатов экспериментального исследования, а также выведением простых законов (период с конца XIX до начала XX в.); в это время в психологии начал использоваться метод факторного анализа, были разработаны различные модификации метода кластерного анализа, был предложен психофизический закон, построена кривая научения и др. [15]

Вторая стадия (период 1940-1950-х годов) была связана с разработкой множества моделей психических процессов и поведения человека с использованием уже известного математического аппарата. [6]

Третий этап (с 1960-х годов по настоящее время) характеризуется выделением математической психологии как отдельной психологической дисциплины, основной целью которой является разработка математического аппарата для моделирования психических процессов и анализа данных психологического эксперимента. [4]

Четвертый этап (еще не наступил), возможно, будет характеризоваться становлением теоретической и отмиранием математической психологии (Леонтьев, 1974). Часто математическую психологию (МП) отождествляют с статистическими методами, что является ошибочным. Можно сказать, что математическая психология и статистические методы соотносятся друг с другом так же, как психология теоретическая и экспериментальная. [2]

Применение статистических методов уже на ранних этапах развития психологической науки неслучайно и является следствием общей тенденции математизации науки. С этой точки зрения в современной науке математическая психология является важной для вновь становящихся областей психологии. [13]

Объектами математической психологии являются индивидуальный и коллективный субъекты, обладающие психическими свойствами, а также содержательные психологические теории и математические модели. Предметом математической психологии является разработка и применение формального аппарата для адекватного моделирования систем, обладающих психическими свойствами, а методом - математическое моделирование. [7]

В основе любого статистического метода анализа данных лежит теоретическая модель изучаемого процесса или явления. В настоящее время статистические методы все больше проникают и в гуманитарные области знаний: в экономику, психологию, социологию, лингвистику. [4]

Благодаря развитию информационных технологий и широкому использованию персональных компьютеров математические методы, казалось бы, должны становиться все более доступными для людей с гуманитарным образом мышления. Однако складывается парадоксальная ситуация. Математическая культура не растет, а падает. [11]

Непрерывное и быстрое расширение областей исследования, в которых удается эффективно использовать математические методы, составляет одну из характерных черт развития современной науки. 5]

Цель исследования: исследовать психологические особенности студентов вузов разных этнических групп, используя статистические методы.

Задачи исследования:

1. Раскрыть сущность статистических методов и их использование в психологии.
2. Определить уровень эмоциональной устойчивости, ригидности, уровень волевой регуляции и т.д. (Многофакторный личностный опросник Кеттелла) исследуемых студентов, с использованием математических методов.
3. Выявить особенности отношений студентов с родителями, с использованием математических методов.
4. Определить межличностные отношения студентов, с использованием математических методов.
5. Определить уровень творческого потенциала студентов, с использованием математических методов.

Объектом изучения являются студенты вуза первых курсов.

Предмет исследования: статистические методы и их применение в психологии.

В ходе исследования были использованы следующие методики:

• Многофакторный личностный опросник Кеттелла.
• Опросник "Взаимодействие родитель - ребенок".
• Модульный тест Анцупова.
• Тест на определение творческого потенциала С.Д. Резнина, С. Н. Соколова и В. В. Бондаренко «Каков ваш творческий потенциал?».

Методы исследования: теоретический анализ литературы по данной теме, психолого-педагогический эксперимент, наблюдение, синтез, обобщение, абстрагирование, статистические методы.

Теоретической базой исследования послужили работы таких исследователей как, Гласс Дж., Стенли Дж., Митина О.В., Бусыгина A.JI., Ведерникова Л.В., Горностаев П.В., Левитская Е.Ю., Легран П., Матушанский Г.У., Менг Т.В., Соломко Л.И. и др.

Экспериментальная база исследования. В исследовании приняли участие студенты первых курсов Университета Дружбы народов города Москвы, в количестве 428 человек.

Структура работы. Работа состоит из введения, 2 глав, заключения и списка использованной литературы.

ГЛАВА 1. СТАТИСТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ

Использование математических методов в психологических исследованиях предполагает создание формального математического аппарата, пригодного для изучения психологических явлений и процессов на специальном объекте - модели, являющейся промежуточным звеном между исследователем и предметом исследования. [12]

Подобное замещение допускается при условии, что реальный объект изучения и его математическая модель имеют сходство в основополагающих элементах и отношениях между ними. Поэтому, изучая модель, можно получить новые данные о предмете исследования, которые в обычных условиях определить достаточно сложно, а в некоторых случаях и невозможно. [14]

Построение математической модели предполагает качественное описание предмета исследования, формулирование статистической гипотезы и ее проверки. [8]

Статистическая гипотеза - это предположение об определенных эмпирических характеристиках распределения в данной совокупности, которое:

а) появляется одновременно с ведущей идеей исследования и ею определяется;

б) возникает на основании известных знаний, но выходит за их пределы;

в) позволяет систематизировать предположения исследователя и представить их в чётком и лаконичном виде;

г) позволяет соединить известные познания с новым, требующим обоснования;

д) экспериментально и практически проверяема. [7]

Статистическая проверка гипотезы представляет собой процедуру обоснованного сопоставления высказанной гипотезы с имеющейся выборкой, осуществляемая при помощи того или иного статистического критерия (метода). Использование статистических методов, к сожалению, не всегда сопровождается четкими представлениями о возможностях и границах их применения, так как в научно-методической литературе нет единого подхода, позволяющего исследователю определиться с выбором статистического критерия, соответствующего задачам педагогического исследования. Рассмотрим в качестве примера некоторые подходы решения проблемы, которые отражают основные аспекты данного вопроса. [16]

Б.А. Сосновский при решении данной проблемы предлагает основываться на мощности критерия - чем выше мощность критерия, тем он предпочтительней. Однако при этом не указывается, как данный критерий будет соответствовать математической модели эмпирического исследования. [5]

Е.В. Сидоренко полагает, что выбор статистического критерия следует, прежде всего, определять, исходя из задач исследования и количества элементов (иерархий) выборки. Однако при этом:

1) соответствие гипотез исследования и статистических гипотез критерия должно устанавливаться самим исследователем, что затрудняет выбор критерия;

2) классификация критериев относительно количества элементов (иерархий) представлена согласно используемым автором статистических таблиц, что неоправданно сужает границы применимости критериев. [8]

Ю.Н. Толстова, основываясь на анализе условий (ограничений) применимости статистических методов, предлагает типологию общепринятых статистических критериев, сводящуюся к простому их перечислению, что мало похоже на классификацию и поэтому затрудняет ее использование. При этом не учитываются задачи и гипотезы исследования, что может привести к некорректным выводам в психологических исследованиях. [12]

А.Д. Наследов отмечает, что выбор критерия определяется статистической гипотезой, но при этом не приводит видов возможных гипотез, ссылаясь на то, что их количество сводится к небольшому числу типичных исследовательских ситуаций, в основу классификаций которых, прежде всего, должны быть положены типы шкал, количество и соотношение сравниваемых групп. Андрей Дмитриевич приводит обоснование этих утверждений, но при этом не дает четких рекомендаций по использованию тех или иных методов, применяемых в психолого-педагогическом исследовании. [3]

Анализ научной и учебно-методической литературы позволил выявить необходимые критерии при выборе статистического метода:

1. Тип переменных (признаков).

2. Шкала, которая использовалась при измерении психолого-педагогических показателей (номинативная, порядковая, интервальная и отношений).

3. Тип распределения данных, который получился в исследовании:

а) нормальное распределение (в этом случае используют параметрические критерии);

б) тип распределения данных не известен (не имеет значения) (применяют непараметрические критерии).

4. Количество элементов в выборке (при небольших объемах выборки испытуемых целесообразно использовать непараметрические критерии, которые дают большую достоверность выводам, независимо от того, получено ли в исследовании нормальное распределение данных или нет).

5. Тип исследовательской задачи (для непараметрических методов: выявление различий в уровне исследуемого признака; оценка сдвига значений исследуемого признака; выявление различий в распределении признака; выявление степени согласованности изменений).

6. Формулировка основной (нулевой) и альтернативной статистических гипотез.

7. Ограничения, которые имеет каждый критерий. [16]

Можно предложить следующую классификацию исследовательских задач и непараметрических методов их решения, учитывающую условия применимости критерия (тип шкалы, количество выборок и замеров) и соответствующие формулировки нулевой и альтернативной статистических гипотез. [1]

Только при соблюдении всех выше перечисленных положений статистическая проверка гипотезы как элемент метода научного исследования позволяет объединить эмпирическое и теоретическое в педагогическом исследовании, т.е. сочетать в ходе изучения педагогического объекта прямое наблюдение, факты, эмпирический уровень исследования с построением логических конструкций и научных абстракций. Таким образом, практическая и познавательная ценность статистической проверки гипотезы определяется ее адекватностью изучаемым сторонам объекта, а также тем, насколько правильно выбран метод для его обоснования, т.е. насколько правильно построено психологическое исследование. [3]

В последнее время происходит интенсивный процесс внедрения количественных методов, основанных на использовании математического аппарата, практически во все отрасли науки. Не составляет исключения и такая наука, как психология. Количественные методы в практике научно-исследовательской работы в этой области используются все более широко и эффективно. [15]

Статистика содержит три главных раздела, к которым относятся: описательная статистика, индуктивная статистика и корреляционный анализ.

1) Описательная статистика, позволяет описывать, подытоживать и воспроизводить в виде таблиц или графиков данные того или иного распределения, вычислять среднее для данного распределения и его размах и дисперсию. Описательная статистика включает в себя табулирование, представление и описание совокупностей данных. Эти данные могут быть либо количественными, как, например, измерения роста и веса, либо качественными, как, например, пол и тип личности. Огромные массивы данных, как правило, должны обобщаться или свертываться, прежде чем они будут интерпретироваться человеком.

Таким образом, описательная статистика служит инструментом, описывающим, обобщающим или сводящим к желаемому виду свойства массивов данных.

2) Задача индуктивной статистики заключается в проверке того, можно ли распространить результаты, полученные на отдельной выборке, на всю популяцию, из которой взята эта выборка. Иными словами, правила этого раздела статистики позволяют выяснить, до какой степени можно путем индукции обобщить на большее число объектов ту или иную закономерность, обнаруженную при изучении их ограниченной группы в ходе какого-либо наблюдения или эксперимента. Таким образом, при помощи индуктивной статистики делают какие-то выводы и обобщения, исходя из данных, полученных при изучении выборки.

3) Корреляционный анализ позволяет узнать, насколько связаны между собой две переменные, с тем, чтобы можно было предсказывать возможные значения одной из них, если мы знаем другую.

Лицам, начинающим изучение статистики, полезно отказаться от широко распространенного представления о статистике. Они должны понимать, что абсурд может найти свое выражение, как в словесной, так и в цифровой форме. Однако знание логики является надежной гарантией от некритичного принятия словесного абсурда, а знание статистики представляет собой лучшую защиту от абсурда цифрового. Первый шаг к замене привычных представлений о статистике на более реальные - это изучение структуры дисциплины «статистические методы» и ее исторических предшественниц. [4]

На первоначальное развитие статистических методов оказало влияние их происхождение. У статистики были «мать», которой нужно было предоставлять регулярные отчеты правительственных подразделений (штат и статистика происходят от одного латинского корня - status), и «отец» - честный карточный игрок, который полагался на математику, усиливавшую его ловкость - умение брать решающие взятки в азартных играх. От матери ведут свое происхождение счет, измерение, описание, табулирование, упорядочение и проведение переписей, то есть все то, что привело к современной описательной статистике. От предприимчивого интеллектуала - отца возникла в конечном счете современная теория статистического вывода, непосредственно базирующаяся на теории вероятностей. Дополнение, называемое планированием экспериментов, опирается и основном на сочетание теории вероятностей с несколько элементарной, но удивительной логикой. [10]

Изучаемые признаки (переменные, variables) делятся на количественные и качественные. Количественными являются признаки, количественная мера которых четко определена, качественными - признаки, не поддающиеся числовому измерению. Количественные признаки подразделяются на непрерывные и дискретные. Непрерывные признаки могут принимать любое значение на непрерывной шкале. Дискретные признаки могут выражаться только целыми числами. Качественные признаки, в свою очередь, делятся на номинальные и порядковые или ранговые. [4]

К номинальным признакам относятся характеристики, с которыми нельзя производить арифметические действия и которые нельзя расположить в порядке возрастания или убывания. Порядковые (ранговые) признаки можно расположить (ранжировать) в логическом порядке, однако невозможно количественно выразить, насколько или во сколько раз. Несмотря на то, что при занесении порядковых признаков в компьютер их часто кодируют с помощью цифр, с ними, в отличие от количественных данных, нельзя производить арифметические действия. [8]

Переменные, которые могут быть отнесены к противоположным категориям, то есть могут принимать только одно из двух значений, называются дихотомическими. Количественные данные при необходимости могут быть представлены в виде ранговых или номинальных. Ранговые переменные можно представить в виде номинальных, но не наоборот. В некоторых случаях, например при применении визуально-аналоговых шкал, ранговые переменные представляют и анализируют как количественные, однако в таких случаях следует с большой осторожностью относиться к интерпретации результатов, так как различия между значениями на одном конце шкалы (например, между 1 и 2) могут быть более выражены, чем на другом (например, между 9 и 10) несмотря на то, что числовое значение различий в обоих случаях равно единице. [16]

Перед тем как описывать количественные данные, всегда следует проводить проверку распределения. Под видом распределения понимают функцию, связывающую значения переменной случайной величины с вероятностью их появления в совокупности. В исследованиях чаще всего проводится «проверка распределения на нормальность». Под нормальным распределением понимают симметричное распределение колоколообразной формы, при котором около 68 % данных отличается от среднего арифметического не более чем на одно, а примерно 95 % - не более чем на два стандартных отклонения в каждую сторону. [1]

Несмотря на то, что нормальное распределение встречается очень часто и играет важную роль в статистике, существуют и другие распределения данных (биномиальное, Пуассона, максвелла, Шарлье, и др.). Проверка распределения производится тремя способами: с помощью описательной статистики, графически и с использованием статистических критериев. [4]

Теория статистического вывода - это формализованная система методов решения задач другого рода, создающих значительные трудности для невооруженного человеческого разума. Этот общий класс задач, как правило, характеризуется попытками вывести свойства большого массива данных путем обследования выборки. [2]

Итак, задача статистического вывода состоит в том, чтобы предсказать свойства всей совокупности, зная свойства только выборки из этой совокупности. Статистические выводы строятся на описательной статистике. Они делаются от частных свойств выборок к частным свойствам совокупности; описания свойств, как выборок, так и совокупностей производятся с помощью методов описательной статистики. [5]

Планирование и анализ экспериментов представляет собой третью важную ветвь статистических методов, разработанную для обнаружения и проверки причинных связей между переменными. Исследователи в области общественных наук имеют дело с причинностью - очень сложным философским понятием. План эксперимента настолько важен при изучении причинных связей, что в некоторых философских системах эксперимент представляет собой их операциональное определение. [14]

Статистические методы помогают психологам описывать данные, делать выводы, а отношения больших массивов данных и изучать причинные зависимости. К статистическим методам, применяемым в психологии относят измерение в психологии; шкалирование; представление данных; описательную статистику; метрику; методы одномерной и многомерной прикладной статистики; многомерное шкалирование; многомерный анализ данных (факторный, кластерный); дисперсионный анализ; анализ данных на компьютере, статистические пакеты; приближенные вычисления; компьютерные методов обработки данных; методы математического моделирования; модели индивидуального и группового поведения, моделирование когнитивных процессов и структур и т.д. [4]

Слово «статистика» определяется Кендаллом и Ваклендом (1957) как «итоговое значение, вычисленное по выборке наблюдений, обычно (но необязательно) как оценка некоторого параметра генеральной совокупности, функция объема выборки». Таким образом, среднее арифметическое чисел 1, 4 и 4, равное трем, представляет собой статистику. А тот факт, что некто имеет двоих детей, - это исходные данные, тогда как среднее число детей в городе есть статистика (в действительности вы можете видеть этих двух детей, но не среднего ребенка). Однако это различие между «статистикой» и «данными» не всегда сохраняется. Некоторые специалисты по прикладной статистике и исследователи пользуются термином «статистика» и в том, « в другом случае, утверждая даже, что имя человека или цвет его волос тоже имеет отношение к статистике. [1]

Раздвигая традиционные рамки «точных наук», расширение областей исследования вовлекает сегодня в свою сферу биологию и социологию, языкознание и психологию, юриспруденцию и историю. Применение математических методов открывает во всех этих областях знания пути для более глубокого проникновения в сущность и закономерности изучаемых явлений, более точного предсказания их развития в различных условиях, а значит и более эффективного управления ими, практического их использования. [7]

ГЛАВА 2. ИССЛЕДОВАНИЕ ПСИХОЛОГИЧЕСКИХОСОБЕННОСТЕЙ СТУДЕНТОВ ВУЗА СТАТИСТИЧЕСКИМИ МЕТОДАМИ

Многофакторный личностный опросник Кеттелла

Опросник Кеттела является одним из наиболее распространенных анкетных методов оценки индивидуально-психологических особенностей личности. Отличительной чертой данного опросника является его ориентация на выявление относительно независимых 16 факторов личности. Каждый фактор образует несколько поверхностных черт, объединенных вокруг одной центральной черты.

Опросник Кеттела включает в себя все виды испытаний - и оценку, и решение теста, и отношение к какому-либо явлению. Предлагаемый опросник состоит из 105 вопросов (форма С) на каждой из которых предлагается три варианта ответов (a, b, c).

Мы провели исследование личностных особенностей группы студентов разных этнических групп (индусы, армяне, русские) первых курсов Университета Дружбы народов города Москвы в количестве 428 человек по методике Кеттелла. Усредненные результаты для студентов разных этнических групп по всем факторам опросника Кеттелла представлены в таблице 1.

Таблица 1

Сопоставление средних значений по факторам теста Кеттелла у студентов разных этнических групп (индусы, армяне, русские)

Факторы	Русские	Индусы	Армяне
А - замкнутость-общительность	6 ±0,6	5,6 ±0,9	6,5 ±0,5
В - низкий интеллект-высокий интеллект	5,8 ±0,3	4,6 ±0,9	5,3 ±0,3
С - эмоц. неустойчивость - эмоц. устойчивость	6,8 ±0,3	6,9 ±0,9	6,8 ±0,3
D -флегматичность-возбудимость	5,4 ±0,1	4,4 ±0,1	5,4 ±0,1
Е - подчиненность-доминантность	6,3 ±0,3	5,2 ±0,7	6,2 ±0,3
F - озабоченность-беспечность	5,0 ±0,0	4,7 ±0,8	4,7 ±0,0
G - недобросовестность-добросовестность	6,0 ±0,5	6,6 ±1,1	6,3 ±0,5
Н - робость-смелость	6,4 ±0,9	5,8 ±0,3	6,5 ±0,9
I - жесткость-мягкость	5,5 ±0,6	5,2 ±0,2	5,6 ±0,6
J - интерес к участию в общих делах-индивидуализм	5,3 ±0,2	5,5 ±1,0	5,5 ±0,2
О - низкая тревожность-высокая тревожность	2,5 ±0,6	3,0 ±0,0	3,0 ±0,6
Q2 - социабельность-самодостаточность	2,5 ±0,4	2,5±1,8	2,0 ±0,4
Q3 - импульсивность-контроль желаний	5,0±0,5	5,6 ±0,6	5,3±0,5
Q4 - расслабленность-напряженность	5,5 ±0,1	5,2 ±0,2	5,8 ±0,1

Результаты исследования мы сравнили с помощью коэффициента ранговой корреляции Спирмена между армянами, русскими и индусами. Различные меры взаимосвязи между переменными (корреляции) используются для интервальных данных (параметрические) и ранговых (непараметрические).

В качестве графического представления используют изображение наблюдений в координатных осях, одна из которых соответствует первой переменной, а вторая - второй. Мы использовали формулу для вычисления разности рангов:

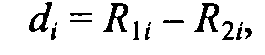
где R1i - ранг, который имеет значение наблюдения i по переменной 1 в ряду значений всех наблюдений по переменной 1; R2i - ранг, который имеет значение наблюдения i по переменной 2 в ряду значений всех наблюдений по переменной 2.

Коэффициент ранговой корреляции Спирмана мы вычисляли по формуле:

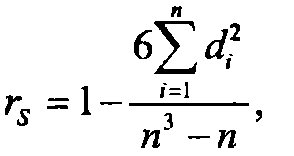
где n - число наблюдений.

Корреляция между факторами не превышает уровня статистической значимости (r= 0,73, r кр = 0,54 при р < 0,05, r кр = 0,68 при р < 0,01; р эмп > р кр.), что свидетельствует о различиях в личностных профилях среди студентов этих этнических групп. Отмечаются различия по факторам: замкнутость - общительность (А), низкий интеллект - высокий интеллект (В), подчиненность - доминантность (Е).

Русские и армяне более социально приспособлены, что обусловлено условиями жизни, обучения и воспитания. По фактору В показатели выше у студентов России, что отражает хороший уровень вербального интеллекта, таких его функций, как обобщение, выделение частного из общего, легкость усвоения новых знаний. Индусы более конформны, зависимы, руководствуются мнением окружающих, не могут отстоять свою точку зрения, осторожны, скромны, послушны (фактор Е).

Мы обнаружили небольшие различия по факторам G - «недобросовестность-добросовестность», Н - «робость-смелость», Q3 - «импульсивность - контроль желаний».

По фактору G у индусов отмечается более развитое чувство ответственности, добросовестность, они стремятся соблюдать моральные требования, обладают хорошим самоконтролем. На выраженность этого фактора большое влияние оказывают «религиозные убеждения», «представления о соответствии определенной социальной группе», которые накладывают ограничения на наследственные свойства индивида.

По фактору H студенты из Армении более смелы, решительны, импульсивны, не испытывают трудностей в общении, легко вступают в контакты, быстро принимают решения. Индусы более скромны, застенчивы, неуверенны, сдержанны, проявляют заботу и внимание к окружающим, хуже поддерживают контакты с широким кругом людей. Анализ фактора Q3 (импульсивность-контроль желаний) свидетельствует о том, что индусы умеют владеть собой, пытаются усвоить признанные нравственные нормы.

Результаты по фактору D (флегматичность - возбудимость) у студентов из Индии ниже нормы. Низкие показатели по фактору D указывают на наличие таких характеристик, как сдержанность, спокойствие, самокритичность, флегматичность, тактичность. Формирование вышеуказанных качеств связано как с особенностями темперамента, так и с условиями воспитания. Армяне имеют самые высокие показатели по этому фактору. Высокая оценка интерпретируется как энергетическая возбужденность, которая требует определенной разрядки; иногда это состояние может превратиться в психосоматическое нарушение: снижается эмоциональная устойчивость, нарушается равновесие, может проявляться агрессивность.

По фактору Q2 (социабельность - самодостаточность) у индусов результаты ниже нормы, что свидетельствует о несамостоятельности, привязанности к группе. В поведении они ориентируются на мнение группы, нуждаются в поддержке и одобрении окружающих. У них отсутствуют инициатива и смелость в выборе собственной линии поведения. В формировании такой модели поведения существенную роль играют как семейные, так и общественные традиции.

Опросник "Взаимодействие родитель - ребенок"

Эмпирическое исследование с целью выявления особенностей семейных взаимоотношений студентов первых курсов Университета Дружбы народов города Москвы в количестве 428 человек.

Опросник "Взаимодействие родитель - ребенок" является "зеркальным" и содержит две параллельных формы: для родителей и для детей. Текст опросника включает 10 шкал - критериев для оценки взаимодействия родителей с детьми.

На каждую шкалу варианта опросника для студентов приходится равное количество вопросов, кроме двух, которые выделяет большинство исследователей, и которые могут считаться базовыми в родительско - детских отношениях. Это шкалы "автономия-контроль" и "отвержение - принятие", в них вошло по 10 утверждений, а в остальные шкалы - по 5 утверждений.

При заполнении опросника студентам и их родителям предлагается оценить степень согласия с каждым утверждением по 5-балльной системе: 1 балл - совершенно не согласен, это утверждение совсем не подходит; 5 баллов - совершенно согласен, это утверждение абсолютно подходит. Для того чтобы выразить это количественно, используют три вида показателей моду, медиану и среднюю.

Мода (Мо) - это самый простой из всех трех показателей. Она соответствует либо наиболее частому значению, либо среднему значению класса с наибольшей частотой.  

Медиана (Me) соответствует центральному значению в последовательном ряду всех полученных значений. В случае если число данных n, четное, медиана равна средней арифметической между значениями, находящимися в ряду на n/2-м и n/2+1-м местах.

Средняя арифметическая (М) - это наиболее часто используемый показатель центральной тенденции. Ее применяют, в частности, в расчетах, необходимых для описания распределения и для его дальнейшего анализа. Ее вычисляют, разделив сумму всех значений данных на число этих данных. Если теперь сравнить все эти три параметра, то будет видно, что при нормальном распределении они более или менее совпадают, а при асимметричном распределении нет.

Для количественной оценки разброса результатов относительно средней в том или ином распределении существуют более точные методы, чем измерение диапазона. Чаще всего для оценки разброса определяют отклонение каждого из полученных значений от средней (М-М), обозначаемое буквой d, а затем вычисляют среднюю арифметическую всех этих отклонений. Чем она больше, тем больше разброс данных и тем более разнородна выборка. Напротив, если эта средняя невелика» то данные больше сконцентрированы относительно их среднего значения и выборка более однородна.

Итак, первый показатель, используемый для оценки разброса, - это среднее отклонение. Его вычисляют следующим образом. Собрав все данные и расположив их в ряд, находят среднюю арифметическую для выборки. Затем вычисляют отклонения каждого значения от средней и суммируют их.

где S(сигма) означает сумму; |d| - абсолютное значение каждого индивидуального отклонения от средней; n - число данных.
Однако абсолютными значениями довольно трудно оперировать в алгебраических формулах, используемых в более сложном статистическом анализе. Поэтому статистики решили пойти по «обходному пути», позволяющему отказаться от значений с отрицательным знаком, а именно возводить все значения в квадрат, а затем делить сумму квадратов на число Формула для вычисления вариансы (дисперсии), таким образом, следующая:

Наконец, чтобы получить показатель, сопоставимый по величине со средним отклонением, статистики решили извлекать из вариансы квадратный корень. При этом получается так называемое стандартное отклонение:

Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок, в знаменателе выражения под корнем надо использовать не n, а n-1:

Стандартное отклонение для популяции обозначается маленькой греческой буквой сигма (), а для выборки - буквой s. Это касается и вариансы, т.е. квадрата стандартного отклонения: для популяции она обозначается 2, а для выборки - s2.)

Результаты расчетов представили в таблице 2. Согласно данным диагностики взаимоотношений родитель-ребенок (в связи с тем, что многие испытуемые из неполных семей диагностировались отношения студента и матери) в целом по выборке испытуемые, удовлетворены сложившимися отношениями с родителями (среднее = 12; медиана = 12; мультимодальное распределение).

Таблица 2

Данные описательной статистики взаимоотношений родитель-ребенок по выборке

Характеристика	Среднее	Медиана	Мода	Частота	Дисперсия	Стандартное отклонение	Ошибка среднего
Требовательность родителей	11,42	12,00	13,00	10	10,28	3,20641	0,413946
Строгость родителей	11,78	12,00	16,00	13	9,43	3,07032	0,396376
Контроль со стороны родителей	10,07	10,00	9,000	12	4,74	2,17744	0,281106
Эмоциональная близость с родителями	10,7	10,00	9,000	13	8,89	2,98187	0,384957
Принятие ребенка родителями	10,87	10,00	8,000	12	8,35	2,89047	0,373158
Сотрудничество	9,75	9,00	9,000	19	4,05	2,01372	0,259971
Согласие между ребенком и родителями	10,1	10,00	9,000	14	4,29	2,07242	0,267548
Последовательность родителей	10,23	11,00	12,00	16	4,18	2,04497	0,264005
Авторитет родителей	10,58	10,00	Multiple		10,15	3,18520	0,411207
Удовлетворенность отношениями с родителями	12,47	12,00	Multiple		20,73	4,55277	0,587760

Идеальными свои отношения с родителями склонны считать 33,3% студентов, остальная часть считает, что их отношения с родителями требуют коррекции.

Модульный тест Анцупова

Основной методикой изучения межличностных отношений в группе исследуемых студентов выступил «Модульный тест Анцупова». Он имеет модульную структуру и тем самым позволяет оценивать в рамках одной методики и межличностные отношения, и некоторые другие характеристики группы, интересующие психолога.

Вариант опросного листа для студентов был сформирован из 2-х основных и 4-х дополнительных модулей. Студентам предлагалось оценить их отношение к каждому и оценить то, как к ним, на их взгляд, относится другой.

Два базовых модуля - «Мое отношение к...» и «Отношение ко мне» - дают возможность оценить реальное отношение студентов к конкретному человеку и воспринимаемое ими отношение конкретного человека к ним. Усредненная оценка по базовым модулям отражает межличностные отношения студента. Усредненная оценка по всем модулям отражает статус студента. На основе первичных оценок по базовым модулям рассчитывались индексы конфликтности межличностных отношений. Оценки выставлялись на специальном бланке, разработанном таким образом, чтобы исключить всякое подозрение опрашиваемых относительно возможности их идентификации по почерку. Процедура опроса занимала около 40-50 минут.

Для проверки значимости и статистической достоверности различий межличностных отношений студентов в рассчитывался 1-критерий Стьюдента. Рассмотрим общую характеристику межличностных отношений студентов (табл. 3).

Тест Стьюдента - это простейший параметрический критерий, когда речь идет о задачах однородности одной и двух выборок. При нахождении критерии Стьюдента использовали формулу:

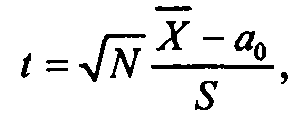
где X - среднее выборки; N - количество наблюдений в выборке; S -стандартное отклонение; а0 - гипотетическое значение среднего. Число степеней свободы равно N-1.

Были выявлены различия на достоверно значимом уровне в показателях объема индивидуального вклада студента в общее дело группы (1=9,270), преобладания групповых интересов над личными (1=9,004), статуса (1=8,353), способности работать в команде (1=5,350), реальных отношений (1=5,259), межличностных отношений в целом (1=4,680) и воспринимаемых отношений (1=3,868).

Таблица 3

Общая характеристика межличностных отношений студентов

Показатель	Девушки	Юноши		Критич. (р=0,05)
	Среднее	Станд. откл.	Среднее	Станд. откл.
Реальные отношения	8,79	0,94	7,98	1,16	5,259	1,980
Воспринимаемые отношения	8,53	0,91	8,00	0,95	3,868	1,980
Межличностные отношения в целом	8,65	0,88	7,99	1,00	4,680	1,980
Способность работать в команде	7,99	1,32	6,92	1,31	5,350	1,980
Групповые интересы- личные интересы	8,12	1,48	6,13	1,38	9,004	1,980
Индивидуальный вклад в общее дело группы	8,85	0,84	7,07	1,34	9,270	1,980
Статус	8,57	0,65	7,20	1,21	8,353	1,980

По сравнению с мальчиками девушки-студентки характеризуются качественно более высоким уровнем реальных отношений, воспринимаемых отношений и межличностных отношений в целом, а также большей способностью работать в команде, более ярко выраженным преобладанием групповых интересов над личными, большим объемом индивидуального вклада в общее дело и более высоким статусом студентов.

Тест на определение творческого потенциала С.Д. Резнина, С. Н. Соколова «Каков ваш творческий потенциал?»

Для определения уровня творческого потенциала студентов мы использовали методику С.Д. Резина. При изучении творческой активности студентов были получены результаты для девушек и юношей. Для определения различий между двумя группами мы применили критерий Колмогорова - Смирнова. Критерий Колмогорова-Смирнова - статистический критерий, использующийся для определения того, подчиняются ли два эмпирических распределения одному закону, либо того, подчиняется ли полученное распределение предполагаемой модели. Являются ли значимыми различия между 2 исследуемыми группами?

Таблица 4

Творческий потенциал студентов по методике С.Д. Резнина, С. Н. Соколова «Каков ваш творческий потенциал?»

Уровень усвоения	Частота в 1 группе (девушки)	Частота в 2 группе (юноши)
Хороший	172 чел.	120 чел.
Приблизительный	36 чел.	49 чел.
Плохой	15 чел.	36 чел.
Объём выборки	n1=172+36+15=223	n2=120+49+36=205

 

Вычисляем относительные частоты f, равные частному от деления частот на объём выборки, для двух имеющихся выборок.

Далее определяем модуль разности соответствующих относительных частот для 2 выборок.

Таблица 5

Модуль разности соответствующих относительных частот для 2 выборок

Относительная частота 1 группы (f1)	Относительная частота 2 группы (f2)	Модуль разности частот |f1– f2|
172/2230.77	120/2050.59	0.18
36/2230.16	49/2050.24	0.08
15/2230.07	36/2050.17	0.1

 

Среди полученных модулей разностей относительных частот выбираем наибольший модуль, который обозначается dmax. В рассматриваемом примере 0.18>0.1>0.08, поэтому dmax=0.18.

Эмпирическое значение критерия эмп определяется с помощью формулы:

Чтобы сделать вывод о схожести по рассматриваемому критерию между двумя группами, сравним экспериментальное значение критерия с его критическим значением, определяемым по специальной таблице, исходя из уровня значимости . В качестве нулевой гипотезы примем утверждение о том, что сравниваемые группы незначительно отличаются друг от друга по уровню усвоения. При этом нулевую гипотезу следует принять в том случае, если наблюдаемое значение критерия не превосходит его критического значения.

Считая, что , по таблице определяем критическое значение критерия: кр(0,05)=1,36.

Таким образом, эмп=1,86>1,36= кр. Следовательно, нулевая гипотеза отвергается, и группы по  рассмотренному признаку отличаются существенно.

Заметим, что объёмы рассматриваемых выборок должны быть достаточно большими: n150, n250.

ЗАКЛЮЧЕНИЕ

При изучении психических явлений психология не может ограничиться исследованием единичных фактов, как бы интересны они сами по себе ни были. Психические процессы - массовое явление, и поэтому присущие им закономерности могут быть выявлены лишь путем исследования массовых фактов. [4]

Статистические методы применяются при анализе полученных в исследовании материалов. Однако правильное применение методов статистики выдвигает серьезные требования и к методике собирания материала в процессе исследования. Обоснованные статистические выводы могут быть сделаны только при наличии достаточного количества подмеченных фактов и при достаточной однородности собранного материала. [12]

Статистический метод опирается на законы больших чисел, а это в ряде случаев требует не менее ста наблюдений. Полученные при статистической обработке материала выводы могут отличаться различной степенью вероятности (объективной возможности повторения или обнаружения при данных условиях). Вероятность сделанного вывода зависит от количества произведенных наблюдений и колеблется от 0 (невозможность данного факта) до 1 (полная достоверность, обязательное наступление при определенных условиях). Математически выведенная зависимость степени вероятности вывода от числа наблюдений представлена в следующей таблице. [17]

Статистические методы исследования теряют свое научное значение, если они применяются для обработки качественно неоднородного материала, например если исследователь будет объединять в одну группу данные, полученные при изучении лиц разного возраста, разной квалификации, разных специальностей и т. д. [6]

СПИСОК ЛИТЕРАТУРЫ