Тема 6. Смертность, средняя ожидаемая продолжительность жизни, самосохранительное поведение
Смертность определяется так же, как и рождаемость, — это частота случаев смерти в социальной среде. Измеряется системой показателей, из которых самый простой — общий коэффициент смертности. О его недостатках уже говорилось в главе 4 (главный из которых — зависимость от половозрастной структуры населения). Лучше всего вовсе не пользоваться общим коэффициентом смертности. А если по каким-либо причинам все же возникает необходимость в этом показателе, желательно устранить или уменьшить влияние на его величину структурных факторов с помощью индексного метода или методов стандартизации коэффициентов (которые рассматриваются далее в этой главе).
6.1. Возрастные коэффициенты смертности
Показатели эти, которые рассчитываются раздельно для мужского и женского полов [1], являются наилучшими для анализа состояния и тенденций уровня смертности. Они рассчитываются по однолетним или пятилетним возрастным группам. Однолетние коэффициенты, конечно, дают наилучшие возможности для подробного анализа, и поэтому профессиональные демографы стараются пользоваться именно ими. Но, во-первых, пользоваться однолетними показателями смертности затруднительно, потому что их очень много (обычно их ограничивают возрастами до 85 лет, но и 84 коэффициента — это не мало). Во-вторых, при использовании однолетних коэффициентов в дело вмешивается возрастная аккумуляция. Поэтом y , если не требуется высокая точность расчетов показателей смертности (такая точность требуется, скажем, при построении математических моделей смертности), то в большинстве случаев для анализа тенденций уровня смертности вполне можно обойтись и пятилетними коэффициентами. Рассчитываются они по формуле:
 (6.1)
(6.1)
где т х — возрастной коэффициент смертности; М х — число умерших в возрасте « х » в календарный период (обычно за год);  х — численность населения в возрасте « х » в середине расчетного периода (обычно среднегодовая).
х — численность населения в возрасте « х » в середине расчетного периода (обычно среднегодовая).
Выражаются возрастные коэффициенты смертности, как и большинство других демографических коэффициентов, в промилле (‰).
6.2. Коэффициент младенческой смертности
Этим коэффициентом измеряется уровень смертности детей в возрасте до 1 года. В прежние годы именовался коэффициентом детской смертности. Теперь различают младенческий — 0 лет — и детский — до 15 лет — возрасты и соответственно младенческую и детскую смертность (в возрасте до 1 года и до 15 лет). Коэффициент младенческой смертности выделяется среди других показателей смертности как своей величиной (вероятность смерти на первом году жизни примерно такая же, как у людей, достигших 55 лет), так и методами расчета и своим социальным значением. Наряду с показателем средней ожидаемой продолжительности жизни коэффициент младенческой смертности служит важной характеристикой условий жизни и культурного уровня населения.
Методы расчета коэффициента младенческой смертности отличаются от методов расчета всех других возрастных коэффициентов. Поскольку уровень смертности детей первого года жизни резко меняется на протяжении года, вычислить среднегодовую их численность представляется затруднительным. Поэтому поступают проще: вместо коэффициента вычисляют вероятность смерти на первом году жизни путем соотнесения случаев смерти детей в возрасте до года не со среднегодовой их численностью, а с общим числом родившихся (однако по старой традиции именуют эту вероятность коэффициентом). Используются в основном три метода расчета коэффициента младенческой смертности, в зависимости от характера исходных данных и требований к точности расчета.
Дети, умершие в возрасте до года в расчетном году « t », принадлежат к двум смежным поколениям родившихся. Часть из них родилась в том же году « t » , в котором они и умерли. Другая часть родилась в предыдущем году « t — 7». Это можно наглядно показать на диаграмме, называемой демографической сеткой. Не будем задерживаться на методологических подробностях построения демографической сетки и пользования ею. Ограничимся лишь описанием сетки в той части, которая необходима нам сейчас для демонстрации соотношения умерших на первом году жизни и родившихся в двух смежных календарных годах.
Демографическая сетка представляет собой систему квадратов (см. рис. 6.1). Горизонтальные линии отсекают годы возраста, вертикальные — годы календарных лет. Число родившихся в календарном году « t » условно изображается в виде точек на оси 0 между вертикальными осями « t » и « t + 1 » , или, иначе говоря, между началом расчетного года и его концом (началом следующего календарного года). По диагоналям от точек на оси 0, символизирующих даты рождения, слева направо и снизу вверх проводятся прямые линии, именуемые линиями жизни. В случае смерти человека линия жизни обрывается, заканчивается точкой смерти. Вот все, что нам пока достаточно знать о демографической сетке.
На сетке можно видеть, что точки смерти детей, умерших в возрасте до года в календарном году « t », образуют квадрат ABCD , который состоит из двух треугольников (элементарных совокупностей умерших) ABC и ACD . Смерти детей, произошедшие в календарном году « t » из числа детей, родившихся в том же году, образуют нижний треугольник ACD , а смерти детей, произошедшие в том же возрасте «0» лет и в том же календарном (расчетном) году « t », но из числа детей, родившихся в предыдущем году « t —1», образуют верхний треугольник того же квадрата — ABC .
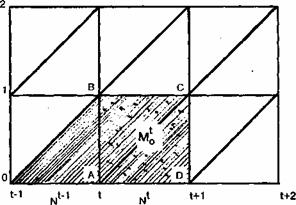
Рис.6.1
Если имеются данные о распределении детей, умерших в возрасте до года, по годам своего рождения (или, иначе говоря, по поколениям), то каждая совокупность умерших детей в возрасте 0 лет соотносится с соответствующим ей числом родившихся. Расчет выглядит в виде следующей формулы:
 (6.2)
(6.2)
где  — коэффициент младенческой смертности в расчетном году « t »;
— коэффициент младенческой смертности в расчетном году « t »;  и
и  — число детей, умерших в возрасте до года из числа родившихся соответственно в расчетном году « t » и предыдущем году « t —1»; N t и N t -1 — — число родившихся соответственно в расчетном году « t » и предыдущем году « t — 1 ».
— число детей, умерших в возрасте до года из числа родившихся соответственно в расчетном году « t » и предыдущем году « t —1»; N t и N t -1 — — число родившихся соответственно в расчетном году « t » и предыдущем году « t — 1 ».
Для применения этой формулы необходимы данные о распределении умерших детей в возрасте до года по поколениям родившихся. Используется же она в тех случаях, когда требуются особенно точные показатели младенческой смертности с большим числом знаков после запятой десятичной дроби. Обычно эта необходимость возникает при построении таблиц смертности (о которых речь пойдет ниже).
Зачастую данных о распределении умерших детей в возрасте до года по поколениям родившихся не оказывается в публикациях, да и необходимости в очень точных измерениях показателей младенческой смертности тоже, как правило, нет. Тогда достаточно бывает воспользоваться методом приближенной оценки уровня младенческой смертности, основанном на эмпирической формуле, которую предложил в начале 1920-х гг. немецкий демограф и математик Йоханнес Ратс (1854—1933):
 (6.3)
(6.3)
где все условные обозначения — те же, что и в предыдущей формуле.
И наконец, простейшая формула, называемая грубым методом, которой, однако, можно пользоваться при определенных условиях. Условия эти — постоянство уровня рождаемости в двух смежных годах, один из которых — расчетный, т.е. тот, за который определяется уровень младенческой смертности, а второй — предшествующий ему. Достаточно просто заглянуть в демографический ежегодник и сравнить показатели рождаемости за указанные годы. Если они одинаковы или мало различаются, можно смело пользоваться «грубым» методом. Он выражается следующей формулой:
 (6.4)
(6.4)
где все условные обозначения известны. Таким образом при этом методе достаточно просто разделить число детей, умерших в расчетном году « t » в возрасте «0» лет, на число родившихся в том же году. Но, повторим, это можно делать только в случае, когда общие коэффициенты рождаемости в расчетном и предшествующем ему годах одинаковы или близки по величине. В случае же существенных различий коэффициентов рождаемости следует использовать формулу Ратса.
Пример расчета. В 1992 г. в России родилось 1 587,6 тыс. детей, в 1993 г. — 1 379,0 тыс., умерло в возрасте менее 1 года соответственно 29,2 и 27,9 тыс. детей. Требуется определить уровень младенческой смертности в 1993 г. грубым методом и методом Ратса.
Решение:
1) грубым методом:  ‰;
‰;
2) по методу Ратса:
 ‰
‰
Как видим, во втором варианте расчета (по методу Ратса) уровень младенческой смертности в нашей стране в 1993 г. был на самом деле значительно ниже, почти на целую промилле (это существенная разница!), чем об этом свидетельствует показатель, рассчитанный грубым методом.
За последнее десятилетие уровень младенческой смертности в России снизился очень мало, с 20,9 ‰ в 1984 г. до 17,2 ‰ в 1997 г. [2] Это не очень высокий уровень, если сравнивать его с аналогичным показателем в нашей же стране лет 30—40 назад (когда он был равен 30—40 ‰ ). Но если сравнивать российский показатель младенческой смертности с аналогичными показателями, которые наблюдаются сегодня в других странах, то он оказывается одним из самых высоких среди экономически развитых стран, в большинстве которых уровень младенческой смертности более чем вдвое ниже, чем в России (т.е. не превышает 8,0 ‰ ). В то же время этот уровень почти стабилизировался, хотя резервы для его дальнейшего снижения еще далеко не исчерпаны. В какой-то степени такой показатель младенческой смертности объясняется переходом нашей статистики с конца 1992 г. на международные принципы учета живо- и мертворождений. До этого времени в российской (а ранее — в советской) статистике живорожденными считались дети, родившиеся при сроке беременности 28 недель и более, с массой тела при рождении 1000 г. и более (или, если масса неизвестна, длиной тела 35 см и более и сделавшие после появления на свет хотя бы один самостоятельный вздох). Дети, родившиеся ранее указанного срока беременности, с массой тела менее 1000 г., учитывались в качестве живорожденных, только если они прожили более 7 суток. Критерии живорождения, установленные Всемирной организацией здравоохранения, были иными. По ним живорожденным признается ребенок, если после появления на свет (независимо от сроков беременности) он дышит или проявляет другие признаки жизни, такие, как сердцебиение, пульсация пуповины или произвольные движения мускулатуры. По оценкам экспертов, переход на критерии живорождения, рекомендованные ВОЗ, может привести к росту величины коэффициента младенческой смертности в России на 25—35% [3]. И если этого пока не случилось, то можно предполагать, что снижение уровня младенческой смертности было на самом деле более существенным, чем об этом можно судить по динамике публикуемых коэффициентов, но это снижение отчасти компенсировалось противоположной динамикой — повышением коэффициента за счет смены критериев живорождения. Кроме того, смена критериев — процесс, очевидно растянутый во времени, и многие статистические и медицинские учреждения не торопятся «испортить» свои учетные данные плохими показателями. Так что видимая на поверхности явлений «стагнация», или медленное снижение коэффициента младенческой смертности, — т.е. тот факт, что коэффициент не растет, — говорит о том, что он наверняка снижается.
В таблице 6.1 показана структура уровня младенческой смертности в России по основным классам причин смерти и ее изменение за последние 10 лет. При некотором снижении общей величины уровня младенческой смертности за данный период, можно видеть, что это снижение происходит за счет снижения смертности от инфекционных и паразитарных болезней и болезней органов дыхания. В то же время возрос уровень смертности и удельный вес случаев смерти (в общей структуре уровня смертности) от таких классов причин смерти, как врожденные аномалии, несчастные случаи, отравления и травмы и особенно—состояния, возникающие в перинатальном периоде [4]. При этом на три класса причин смерти — от врожденных аномалий, от состояний, возникающих в перинатальный период, и от несчастных случаев, отравлений и травм — приходится в сумме 72,0% (три четверти!) всех случаев смерти на первом году жизни. А ведь это причины смерти, обусловленные главным образом поведением и образом жизни матерей.
Таблица 6.1
Структура уровня младенческой смертности в России по основным классам причин смерти
|
Умершие в возрасте до 1 года в расчете на 10 000 родившихся
|
То же в процентах к общей величине коэффициента |
1985 |
1990 |
1997 |
1985 |
1990 |
1997 |
Всего умерших в возрасте до 1 года, в том числе от: |
207,2
|
174,0
|
171,5
|
100,0
|
100,0
|
100,0
|
инфекционных и паразитарных болезней |
24,0 |
13,4 |
10,8 |
11,6 |
7,7 |
6,3 |
болезней органов дыхания |
48,2 |
24,7 |
22 , 6 |
23,3 |
14,2 |
13,2 |
врожденных аномалий |
36,7 |
37,0 |
42,0 |
17,7 |
21,3 |
24,5 |
состояний, возникающих в перинатальном периоде |
77,7 |
80,1 |
72,4 |
37,5 |
46,0 |
42,2 |
несчастных случаев, отравлений и травм |
9,0 |
7,1 |
10,0 |
4,3 |
4,1 |
5,8 |
Всех прочих причин |
11,6 |
11,7 |
13,7 |
5,6 |
6,7 |
8,0 |
6.3. Применение индексного метода в анализе динамики общего коэффициента смертности
Возрастные коэффициенты смертности, как уже отмечалось, дают наилучшие возможности для анализа уровня смертности. Но у них есть недостаток, такой же как у всех других возрастных коэффициентов: их много, с ними трудно работать. Нужен один, обобщающий показатель. Но такого показателя смертности, аналогичного суммарному коэффициенту рождаемости, нет (в определенной степени эту роль выполняет показатель средней ожидаемой продолжительности жизни, но для его получения нужно строить довольно трудоемкие таблицы смертности).
В известной степени можно компенсировать трудности анализа возрастных коэффициентов смертности, повышая аналитические возможности общего коэффициента смертности с помощью индексного метода и методов стандартизации коэффициентов. Для применения этих методов обратимся к общему коэффициенту смертности и представим его в такой форме, чтобы можно было видеть его внутреннюю структуру.
 (6.5)
(6.5)
Первая дробь в правой части формулы есть уже известное отношение годового общего числа умерших М к среднегодовой численности населения. Числитель этой дроби — М — можно представить как сумму произведений возрастных коэффициентов смертности т x на численности населения каждой соответствующей возрастной группы Р х , т.е.  . В знаменателе этой дроби общую численность населения Р можно представить как сумму численностей населения всех возрастных групп, т.е. a P x . Для расчета удобнее численность населения каждой возрастной группы использовать не в абсолютном, а в относительном выражении, в долях единицы или в процентах (приняв соответственно общую численность населения за 1 или за 100. В долях единицы рассчитывать удобнее всего, тогда знаменатель третьей дроби, равный единице, можно опустить).
. В знаменателе этой дроби общую численность населения Р можно представить как сумму численностей населения всех возрастных групп, т.е. a P x . Для расчета удобнее численность населения каждой возрастной группы использовать не в абсолютном, а в относительном выражении, в долях единицы или в процентах (приняв соответственно общую численность населения за 1 или за 100. В долях единицы рассчитывать удобнее всего, тогда знаменатель третьей дроби, равный единице, можно опустить).
Сравнение двух общих коэффициентов смертности теперь можно представить таким образом:
 (6.7)
(6.7)
Индексный метод в данном случае можно применить, если известны все структурные элементы сравниваемых совокупностей, т.е. возрастные коэффициенты смертности т x , и возрастные структуры сравниваемых населений (удельный вес возрастных групп в общей численности населения w x ). Правые верхние индексы 0 и 1 обозначают сравниваемые совокупности населения (либо на начало и конец изучаемого периода времени, если анализируется динамика уровня смертности, либо между собой, если анализируются различия смертности двух групп населения в статике). Итак, рассмотрим случай, когда все структурные элементы коэффициента смертности нам известны и воз можно использовать индексный метод. Построим систему индексов. Для этого в правой части равенства введем в числитель и знаменатель одно и то же число  (т.е. величину общего коэффициента смертности при предположении о неизменности, одинаковости возрастной структуры сравниваемых населений), затем произведем несложную перестановку:
(т.е. величину общего коэффициента смертности при предположении о неизменности, одинаковости возрастной структуры сравниваемых населений), затем произведем несложную перестановку:
 (6.7)
(6.7)
В правой части нашего уравнения оказались два индекса-дроби. Первая из них характеризует изменение (или отличие) общего коэффициента смертности за счет различий именно смертности (повозрастной интенсивности смертности) при неизменной возрастной структуре (доли каждой возрастной группы в составе общей численности населения одинаковы в числителе и знаменателе). Второй индекс характеризует изменение (либо отличие) общего коэффициента смертности за счет изменения (или отличия) возрастной структуры населения. Отметим также, что сумма произведений возрастных коэффициентов смертности на доли соответствующих возрастных групп в численности населения (  ) есть не что иное, как общий коэффициент смертности, и произведем соответствующие замены в знаменателе первой дроби и в числителе второй. Теперь система индексов получает законченный вид.
) есть не что иное, как общий коэффициент смертности, и произведем соответствующие замены в знаменателе первой дроби и в числителе второй. Теперь система индексов получает законченный вид.
Для примера проанализируем динамику уровня смертности населения России за время между серединами 1990 и 1995 гг. (таблица 6.2). Все исходные данные заимствованы из Демографического ежегодника России.
Подставив в формулу числовые значения, получим:

В результате окончательно получаем:
 ,
,
где J m — индекс динамики общего коэффициента смертности; J mx — индекс изменения общего коэффициента смертности за счет интенсивности смертности; J w x — индекс изменения общего коэффициента смертности за счет изменения возрастной структуры населения.
Общий вывод в итоге следующий. За период 1990—1995 гг. общий коэффициент смертности населения в России повысился на 33,9%, в том числе на 26,5% — за счет действительного роста смертности и на 5,9% — за счет изменения (постарения) возрастной структуры населения. Таким образом, если нас интересует динамика уровня смертности, а не показателя (и чаще всего это именно так), то уровень смертности в России за рассматриваемый период времени повысился на 28%, а не на 34, как об этом можно судить по величине общего коэффициента смертности. Разница существенная, и ею, вероятно, не стоит пренебрегать.
6.4. Методы стандартизации коэффициентов
Для применения индексного метода требуются данные о структурных элементах, от которых зависит величина общего коэффициента. К сожалению, необходимые данные не всегда имеются. В таком случае можно использовать так называемые методы стандартизации коэффициентов. В зависимости от характера исходных данных, которыми располагает аналитик, используются обычно два метода стандартизации коэффициентов: прямой и косвенный.
Таблица 6.2
Расчет факторов изменения уровня смертности в России в 1990—1995 гг.
Возрастные группы (лет) |
Доля каждой возрастной группы в общей численности населения на середину 1990 г. (в долях единицы, ω1990x) |
Возрастные коэффициенты смертности (в промилле, m1995x) |
ω1990xm1995x
|
0—4 |
0,0745 |
4,1 |
0,3055 |
5—9 |
0,0818 |
0,6 |
0,0491 |
10—14 |
0,0780 |
0,5 |
0,0390 |
15—19 |
0,0688 |
1,6 |
0,1101 |
20—24 |
0,0618 |
2,7 |
0,1669 |
25—29 |
0,0754 |
3,4 |
0,2564 |
30—34 |
0,0844 |
4,6 |
0,3882 |
35—39 |
0,0778 |
6,3 |
0,4901 |
40—44 |
0,0629 |
8,9 |
0,5598 |
45 — 4 9 |
0,0607 |
12,3 |
0,7466 |
50—54 |
0,0687 |
17,1 |
1,1748 |
55—59 |
0,0506 |
21,4 |
1,0828 |
60—64 |
0,0574 |
29,7 |
1,7048 |
65—69 |
0,0346 |
39,2 |
1,3563 |
70—74 |
0,0217 |
51,3 |
1,1132 |
75—79 |
0,0222 |
78,2 |
1,7360 |
80—84 |
0,0123 |
123,2 |
1,5154 |
85 и старше |
0,0064 |
214,4 |
1,3722 |
Итого |
1,0000 |
|
14,1672 |
6.4.1. Прямой метод стандартизации
Если в распоряжении исследователя имеются возрастные коэффициенты смертности, но неизвестны данные о возрастной структуре сравниваемых населений, то индексный метод применить невозможно. В таком случае можно использовать прямой метод стандартизации. В принципе этот метод очень схож с индексным методом. Разница лишь в том, что неизвестные данные о фактической возрастной структуре населений (как правило, отличной друг от друга) заменяются произвольно выбранной структурой другого населения (одного для всех сравниваемых населений). Таким путем влияние различий возрастной структуры на величины общих коэффициентов устраняется (элиминируется), они искусственно (условно) приводятся к одинаковой возрастной структуре, которая принимается за стандарт (слово «стандарт» в данном случае, так же как и «стандартизация», вряд ли можно признать удачным наименованием, но это уже очень старая всемирная традиция, и к ней привыкли все специалисты).
Вернемся снова к формуле общего коэффициента смертности в ее структурном выражении: т = т x w x , где все условные обозначения те же, что и в предыдущем разделе (об индексном методе). Предположим, что мы хотим сравнить два или более общих коэффициента смертности и при этом установить, в какой степени различия между этими коэффициентами (в динамике или в статике) обусловлены различиями в уровнях смертности и в какой — различиями возрастных структур сравниваемых населений (или населения, если выясняется изменение уровня смертности одного и того же населения в динамике). При этом напомню, что по условию ни одна из возрастных структур нам не известна. Формула, приведенная в начале этого абзаца, примет следующий вид: m СТ = m x w x 0 , где т СТ — стандартизованный общий коэффициент смертности; т х , — фактические возрастные коэффициенты смертности; w х 0 — возрастная структура населения, принятого за стандарт (или, как говорят, «стандарт-населения»).
Рассмотрим теперь применение прямого метода стандартизации коэффициентов смертности на том же примере, который использовался для демонстрации индексного метода в предыдущем параметре. Делаю это для того, чтобы можно было сравнить результаты применения разных методов для одной и той же цели (таблица 6.3).
Таблица 6.3
Стандартизация динамики общих коэффициентов смертности населения России за 1990—1995 гг. прямым методом
Возрастные группы (лет) |
Возрастные коэффициенты смертности mx, ‰
|
Возрастная структура населения Украины по переписи 1989 г., принятая за стандарт ω0x, в долях единицы |
mxω0x |
1990 |
1995 |
1990 |
1995 |
0—4 |
3,9 |
4,1 |
0,0737 |
0,2874 |
0,3022 |
5—9 |
0,5 |
0,6 |
0,0718 |
0,0359 |
0,0431 |
10—14 |
0,4 |
0,5 |
0,0703 |
0,0281 |
0,0352 |
15—19 |
1,1 |
1,6 |
0,0690 |
0,0759 |
0,1104 |
20—24 |
1,7 |
2,7 |
0,0652 |
0,1108 |
0,1760 |
25—29 |
2,1 |
3,4 |
0,0769 |
0,1615 |
0,2615 |
30—34 |
2,7 |
4,6 |
0,0758 |
0,1819 |
0,3487 |
35—39 |
3,6 |
6,3 |
0,0727 |
0,2617 |
0,4580 |
40—44 |
5,0 |
8,9 |
0,0526 |
0,2630 |
0,4681 |
45 — 49 |
7,6 |
12,3 |
0,0626 |
0,4758 |
0,7700 |
50—54 |
10,3 |
17,1 |
0,0720 |
0,7416 |
1,2312 |
55—59 |
15,2 |
21,4 |
0,0574 |
0,8725 |
1 ,2284 |
60—64 |
22,0 |
29,7 |
0,0628 |
1,3816 |
1 ,8652 |
65—69 |
29,6 |
39,2 |
0,0393 |
1,1633 |
1 ,5406 |
70—74 |
45,7 |
51,3 |
0,0275 |
1,2568 |
1 ,4108 |
75—79 |
71,6 |
78,2 |
0,0277 |
1,9833 |
2 ,1661 |
80—84 |
114,4 |
123,2 |
0,0150 |
1,7160 |
1 ,8480 |
85 и старше |
201,8 |
214,4 |
0,0077 |
1,5539 |
1 ,6509 |
Итого |
11,2 |
15,0 |
1,0000 |
12,5510 |
15,9144 |
Теперь вычислим индексы динамики общих коэффициентов смертности в России за 1990 — 1995 гг. Индекс динамики фактических общих коэффициентов уже известен из предыдущего раздела. Он равен:

Индекс динамики стандартизованных коэффициентов смертности будет иным:

Хотя по условию задачи нам не известна возрастная структура на начало и конец изучаемого периода, мы можем узнать ее влияние на динамику общего коэффициента смертности. Для этого вспомним взаимосвязь трех индексов динамики общего коэффициента смертности из предыдущего раздела: J m = J mx x J w x , т.е. индекс динамики фактических общих коэффициентов смертности равен произведению двух индексов, первый из которых характеризует изменение величины общего коэффициента смертности за счет действительного изменения смертности, а второй индекс — изменение той же величины общего коэффициента смертности за счет изменения возрастной структуры населения. Таким образом, по двум известным элементам вышеприведенного уравнения взаимосвязи трех индексов нетрудно определить третий индекс:
 . Отсюда: 1,339/1,268 = 1,056.
. Отсюда: 1,339/1,268 = 1,056.
Окончательный вывод: уровень смертности населения в России увеличился за 1990—1995 гг. на 26,8% (а не на 33,9%, как свидетельствует изменение общего коэффициента смертности), а еще 5,6% роста — результат изменения (постарения) возрастной структуры населения. Полученные прямым методом стандартизации коэффициентов результаты несколько отличаются от аналогичных результатов, полученных с помощью индексного метода. Это результат грубости расчетов, их приблизительности. Но все же различия невелики.
6.4.2. Косвенный метод стандартизации
Если в распоряжении исследователя имеются данные о возрастной структуре сравниваемых совокупностей населения, но неизвестны возрастные коэффициенты смертности и нет исходных данных для их расчета, то можно произвести стандартизацию коэффициентов косвенным методом. В этом случае за стандарт принимаются возрастные коэффициенты какого-либо населения, которые можно найти в статистических справочниках.
При этом методе стандартизация производится косвенно, т.е. мы задаемся вопросом, каким было бы общее число умерших, если бы возрастные коэффициенты смертности во всех сравниваемых группах были бы одинаковыми и именно такими как в стандарт-населении (т.е. в населении, принятом за стандарт). Это рассуждение можно выразить в виде формулы: M = a М х = a P x m x , или, если эту формулу пересказать словами, она означает, что общее число умерших M равно сумме умерших во всех возрастных группах a М x , которая, в свою очередь, может быть представлена в виде суммы произведений численности населения каждой возрастной группы на соответствующий ей возрастной коэффициент смертности. По условию нам известны возрастные структуры сравниваемых групп населения, но неизвестны их возрастные коэффициенты смертности. Поэтому заменяем неизвестные возрастные фактические коэффициенты смертности произвольно подобранными (из справочника, относящимися к любому населению, о котором мы все же априори знаем, что его повозрастная смертность не слишком отличается от смертности в сравниваемых населениях). Используя возрастные коэффициенты смертности населения, принятого за стандарт, получаем так называемые условные числа умерших, т. е. числа умерших, какими они были бы при условии, что повозрастная смертность во всех сравниваемых группах населения одинакова и такая, как в населении, принятом за стандарт. В виде формулы это можно изобразить таким образом: М 0 = a P x х т х 0 , где M 0 ? условное число умерших, Р х — фактические возрастные структуры сравниваемых населений, и т х 0 ? возрастные коэффициенты смертности населения, принятые за стандарт. Сравнивая затем фактическое число умерших в каждом населении с соответствующим этому населению условным числом умерших, получаем индекс, показывающий, насколько фактическая повозрастная смертность в сравниваемом населении (или группе населения) отличается от смертности стандарт-населения. Умножая этот индекс на общий коэффициент смертности стандарт-населения ( т 0 ) , получаем в итоге стандартизованный коэффициент смертности для каждого сравниваемого населения. Окончательно наши рассуждения удобно выразить следующей формулой:
 (6.8)
(6.8)
где т C Т — стандартизованный общий коэффициент смертности; Р х — возрастные группы сравниваемого населения; М — общее число умерших в сравниваемом населении; т х 0 — возрастные коэффициенты смертности населения, принятого за стандарт, и т 0 — общий коэффициент смертности населения, принятого за стандарт.
Но расчет самих стандартизованных коэффициентов смертности для проведения сравнений уровней смертности на самом деле вовсе не обязателен. Это, скорее всего, лишь дань привычке, уступка нашему желанию увидеть коэффициенты смертности в привычном виде. Однако эта привычка не безобидна, так как заставляет некоторых аналитиков трактовать величину стандартизованного коэффициента аналогично фактической. В этом случае нередко рассуждают так: «Фактические коэффициенты измеряют процесс неправильно, потому что их величина зависит от особенностей возрастной структуры. А стандартизованные коэффициенты (их величина) отражают уровень демографического процесса правильно, потому что они свободны от влияния возрастной структуры». Между тем величина стандартизованного коэффициента вовсе не характеризует уровень смертности. Сама по себе она — условна, самостоятельного значения не имеет никакого (ведь она во многом зависит от особенностей возрастной структуры стандарт-населения).
Поэтому вполне можно ограничиться расчетом индексов, выражающих соотношение фактических и условных чисел умерших, с последующим сравнением между собой уже этих индексов. Представим это рассуждение в виде формулы:
J m СТ  (6.9)
(6.9)
где все условные обозначения известны из предыдущей формулы. От подобного упрощения расчет станет только точнее (за счет сокращения количества округлений).
В качестве примера сравним уровни смертности мужского и женского населения России в 1995 г. [5] (таблица 6.4). Общие коэффициенты смертности мужского и женского населения России в 1995 г. составили соответственно 16,9 и 13,3 ‰. Отсюда определяем, что уровень смертности мужчин выше, чем женщин, на 16,9/13,3 = 1,271, т.е. на 27,1%. Это немало, но с такой разницей можно было бы согласиться. Однако мы догадываемся, что именно в силу более высокой продолжительности жизни женщин по сравнению с мужчинами их возрастная структура в среднем старше аналогичной структуры мужского населения. Стандартизация коэффициентов смертности позволяет устранить (элиминировать) влияние различий возрастной структуры мужского и женского населения на величину общих коэффициентов смертности, так сказать, уравнять их в этом отношении. Окончательный расчет по формуле будет таким:
J m СТ = 1197048 / 779467 х 1428193 / 1055541 = 1,536 х 1,353 = 2,078
Результат расчета показывает, что на самом деле смертность мужчин выше, чем смертность женщин, не на 27%, а в 2,1 раза. Это уже явно ничем не оправданная и нетерпимая разница в продолжительности жизни, имеющая далеко идущие и многообразные демографические и другие социальные последствия.
В заключение этого раздела хочу обратить внимание на два очень важных обстоятельства, связанных с использованием методов стандартизации коэффициентов.
Во-первых, не существует какого-либо формализованного способа выбора (подбора) стандарт-населения. Это делается на основе опыта. Подбирается население — его параметры (возрастная структура при прямом методе стандартизации — или возрастные коэффициенты смертности — при косвенном методе), — о котором априори известно, что оно по этим параметрам схоже с теми населениями, уровни демографических процессов которых (любых, не обязательно только смертности) сравниваются между собой. Если сравниваются населения с резко различающимися возрастными структурами, то параметры стандарт-населения выбираются таким образом, чтобы они были средними между параметрами сравниваемых населений (предполагаемых или известных за другие годы и т.п.).
Таблица 6.4
Стандартизация общих коэффициентов смертности мужского и женского населения России в 1995 г. косвенным методом
Возрастные группы (лет)
|
Численность населения на середину 1995 г. (тыс. человек) Рх |
Возрастные коэффициенты смертности стандарт-населения в промилле mx0 |
Условное число умерших Рх х mx
|
Мужчины |
Женщины |
Мужчины |
Женщины |
0 ? 4 |
3892 |
3693 |
4,1 |
15957 |
15141 |
5—9 |
5856 |
5606 |
0,6 |
3514 |
3364 |
10—14 |
6059 |
5861 |
0,5 |
3030 |
2931 |
15—19 |
5525 |
5367 |
1,6 |
8840 |
8587 |
20—24 |
5275 |
5042 |
2,7 |
8440 |
8067 |
25—29 |
4896 |
4632 |
3,4 |
16646 |
15749 |
30—34 |
5728 |
5641 |
4,6 |
26349 |
25949 |
35—39 |
6396 |
6477 |
6,3 |
40295 |
40805 |
40 ? 44 |
5838 |
6081 |
8,9 |
51958 |
54121 |
45—49 |
4755 |
5134 |
12,3 |
58487 |
63148 |
50—54 |
2462 |
2888 |
17,1 |
42100 |
49385 |
55—59 |
4308 |
5460 |
21,4 |
92191 |
116844 |
60—64 |
2861 |
3965 |
29,7 |
84972 |
117761 |
65—69 |
2906 |
4764 |
39,2 |
113915 |
186749 |
70—74 |
1279 |
3298 |
51,3 |
65613 |
169187 |
75—79 |
600 |
1808 |
78,2 |
46920 |
141386 |
80—84 |
436 |
1629 |
123,2 |
53715 |
200693 |
85 и старше |
217 |
974 |
214,4 |
46525 |
208826 |
Всего |
69289 |
78320 |
15,0 |
779467 |
1428193 |
Во-вторых, считаю необходимым повторно предупредить читателя о том, что сама по себе величина стандартизованных коэффициентов носит условный характер, зависит от выбранного стандарта (стандарт-населения), поэтому она не имеет никакого самостоятельного значения. Имеет значение только разница между стандартизованными коэффициентами, которая в идеале остается неизменной при любом стандарте (небольшая разница в результатах может быть следствием грубости расчета, округлений цифр либо не очень удачного выбора стандарт-населения, если оно по своим характеристикам очень сильно отличается от сравниваемых населений).
6.5. Вероятностные таблицы смертности (чаще называемые просто таблицами смертности)
Это самый совершенный инструмент для анализа состояния и тенденций уровня смертности. Они представляют собой систему взаимосвязанных показателей, характеризующих изменение вероятности смерти по мере увеличения возраста людей, или, напротив, изменение вероятности дожития до некоторого возраста, а также среднюю продолжительность жизни некоторого поколения родившихся. Иначе говоря, таблицы смертности описывают последовательность и скорость вымирания поколения.
Показатели (колонки) таблиц смертности:
- l x — числа доживающих до возраста « х » лет;
- d x — числа умирающих в возрасте « х » лет (т.е. в возрастном интервале от « х » до « х + 1 »);
- q x — вероятность умереть в возрасте « х » (т.е. в возрастном интервале от « х » до «х + 1 »);
- р х — вероятность для доживших до возраста « х » дожить и до следующего года возраста « х + 1 »;
- L x — числа живущих в возрасте « x » (в возрастном интервале от « х » до « х + 1 »;
- Т х — числа живущих в возрасте « х » лет и старше (число человеко-лет предстоящей жизни для данного поколения);
- е 0 — средняя ожидаемая продолжительность жизни для новорожденных;
- е х — средняя ожидаемая продолжительность жизни для достигших возраста « х ».
В таблицах смертности принимают первоначальную численность поколения (число родившихся, основание или корень таблицы смертности) неизменной во времени и равной единице и прослеживают, как с переходом от возраста к возрасту, от 0 до предельного возраста (100 лет или 100 с небольшим) первоначальная совокупность поколения родившихся убывает в результате смерти от 1 до 0.
Отсюда следует, что в таблицах смертности все числа, кроме числа родившихся, равного 1, меньше 1, т. е. дроби. Чтобы избежать большого количества дробных чисел, число родившихся (основание таблицы) в практических расчетах принимают равным 100000 или 10000, в зависимости от желаемой значности (точности) расчетов. Но не менее 10000.
Различают таблицы полные и краткие. В полных таблицах возрастные интервалы равны одному году, в кратких — пяти годам. Целесообразно рассмотреть взаимосвязи показателей таблиц смертности на примере полных таблиц. В них с переходом от возраста « х » к возрасту « х + 1 » число доживающих l x будет последовательно уменьшаться на величину числа умирающих в возрасте « х », т.е. d x . Математически эта связь выглядит следующим образом:
L x +1 = l x – d x (6.5.1)
Если проследить эту последовательность (порядок) вымирания поколения, начиная с основания таблицы смертности, то она будет выглядеть следующим образом: l 0 = 1 или 10000 или чаще 100000 – d 0 = l 1 – d 1 = l 2 – d 2 = l 3 и т.д. В общем виде эту последовательность можно записать так: l x +1 = l x – d x (для полных таблиц) и l х+п = l x – d x + n , где п — длина возрастного интервала.
Каждый родившийся рано или поздно умирает, и в конечном счете число умерших (из каждого поколения, численность которых мы определили заранее) составит l 0 , т. е. число родившихся, или

где w –1 — предельный возраст, до которого доживает последний человек из поколения родившихся.
Формула (6.5.1) может быть использована в различных перестановках, к примеру:
l x = l x +1 + d x ; d x = l x – l x +1 , и т.д.
Вероятность смерти в возрасте « х » (в возрастном интервале от « х » до « х + 1 ») ? q x — определяется в соответствии с правилами теории вероятностей как отношение числа умирающих в возрасте « х » – d x к числу доживающих до этого возраста, т.е. l z . В виде формулы эта связь выглядит так:
 (6.5.2)
(6.5.2)
Из формулы хорошо видно, что вероятность смерти q x можно интерпретировать и как долю умирающих в возрасте « х » из числа доживающих до начала возрастного интервала « х ».
Напротив, вероятность дожития до возраста «х + 1» — р х для тех, кто дожил до возраста « х » (до начала возрастного интервала « х »), будет определяться как отношение числа доживающих до возраста « х + 1» к числу доживших до возраста « х » (до начала возрастного интервала « х »). Запишем эту связь в виде формулы:
 (6.5.3)
(6.5.3)
Отсюда можно так же, как и в предыдущей формуле, видеть, что вероятность дожития есть не что иное, как доля переживающих возраст « х » из числа доживающих до его начала.
Формулы (6.5.2) и (6.5.3) так же, как и (6.5.1), используются в виде различных преобразований, например: l x +1 = l x р х ; d x = l x q x b и т. д.
Поскольку мы рассматриваем смертность, то в пределах одного возрастного интервала возможна только единственная альтернатива: либо пережить этот интервал и благополучно отметить следующий день рождения, либо, увы, не дожить до него. Иначе говоря, сумма вероятностей дожития до следующего возраста либо умереть, не дожив до него, равна единице, что можно изобразить в виде формулы:
q x + р х = 1. (6.5.4)
Эта простейшая формула оказывается, однако, очень полезной, так как, зная одну из двух вероятностей, всегда легко найти вторую (вычитанием из единицы).
Начав прослеживать закономерное уменьшение чисел доживающих с основания таблицы смертности, замечаем вскоре, что: l 1 = l 0 p 0 .
Если основание таблицы l 0 = 1, то, естественно, l 0 в формуле можно опустить, и она примет вид: l 1 = р 0 .
Далее, следуя той же логике: l 2 = l 1 p 1 . Подставим вместо l 1 его значение из предыдущей формулы ( l 1 = р 0 ). Получим: l 2 = р 0 p 1 . Затем: l 3 = l 2 р 2 = p 0 p 1 p 2 и т.д. Отсюда, кстати, видно, что число доживающих — нечто иное, как произведение вероятностей дожития, или, иначе говоря, оно само — тоже вероятность, вероятность для новорожденного дожить до возраста « х ». В обобщенном виде эту связь можно записать и так:
l x = p 0 p 1 p 3 x ………. x p x-1 . (6.5.5)
Поскольку в практических расчетах основание таблицы смертности принимается равным не 1, а 10000 и чаще всего 100000, то l 0 опускать не приходится и формула (6.5.5) выражается в следующем виде:
l x = l 0 p 0 p 1 p 2 p 3 x ………. x p x-1 .
Здесь, пожалуй, самое время сказать, что в таблицах смертности нет ни одного доживающего или умирающего. Вообще — ни одного человека. Одна смерть в чистом виде. Одни вероятности и доли. В этом их большое преимущество перед другими измерителями уровня смертности, поскольку при отсутствии человека нет и зависимости показателей таблиц смертности от возрастной структуры населения. Наименования «числа доживающих», «числа умирающих» — опять же условные наименования, не более того.

Рис.6.2. Вероятность умереть qx для мужского и женского населения СССР, 1986—1987 гг.
Последовательность изменений чисел доживающих l x графически представляет собой линию дожития, характеризующую порядок вымирания поколения. Чем ниже уровень смертности, чем большая доля родившихся (поколения) доживает до старших возрастов, тем более выпуклой формы будет кривая дожития (см. рис.6.4).
Числа живущих. В таблицах смертности числа доживающих показывают долю остающихся в живых к началу каждого следующего года возраста, то есть к возрасту « x » лет остается в живых часть поколения l x , к возрасту « х + 1» — часть l x +1 , и т.д.
Однако на самом деле при переходе от одного возраста к следующему численность поколения убывает непрерывно, поэтому число живущих в возрасте « х » есть некоторая средняя величина между значениями чисел доживающих l x и l x +1 . Если разбить каждый год возраста на предельно малые промежутки времени и с помощью дифференциального исчисления определить средние величины живущих в каждом таком мельчайшем интервале, то изменение чисел живущих определяется путем интегрирования таких средних. В реальности интегрирование заменяется суммированием.

Рис.6.3. Число умирающих dx мужчин и женщин СССР, 1986—1987 гг.
На практике обычно мы не располагаем значениями чисел доживающих l x , для более дробных возрастных интервалов, чем год. Поэтому для средних возрастов, в которых число доживающих изменяется почти прямолинейно, число живущих рассчитывается как обычная средняя арифметическая величина из двух чисел доживающих, на начало и конец возрастного интервала, т. е.:
 (6.5.6)
(6.5.6)
На тех же участках кривой дожития, где ее кривизна значительна, число живущих определяют по формуле, учитывающей эту кривизну:
 (6.5.7)
(6.5.7)
где d x — число умирающих в таблицах смертности; т х — возрастные коэффициенты смертности того же населения, для которого строились таблицы смертности.
Обычно по формуле (6.5.7) рассчитывают число живущих для всех участков кривой дожития, кроме самых первых детских возрастов, для которых используются специальные формулы (мы познакомимся с ними позднее, при построении краткой таблицы смертности).
Средняя ожидаемая продолжительность жизни. Число живущих можно трактовать также и как число человеко-лет, прожитых всем поколением родившихся в интервале возраста « x ». Тогда, следовательно,

Рис.6.4. Линии дожития lx мужского и женского населения СССР, 1926—1927, 1958—1959, 1986—1987 гг.
поколение родившихся l 0 проживет на первом году жизни (т.е. в возрасте 0 лет) L 0 лет, на 2-м году — L i лет, на 3-м — l 2 лет и т.д., а всего:
 (6.5.8)
(6.5.8)
где Т 0 — число человеко-лет, которое предстоит прожить данному поколению родившихся.
Если эту сумму человеко-лет разделить на первоначальную численность поколения, т.е. на число родившихся l 0 , то получим очень важный социальный показатель, который называется показателем средней ожидаемой продолжительности жизни.
Средняя ожидаемая продолжительность предстоящей жизни [6] — это число лет, которое проживет один человек в среднем из данного поколения родившихся при условии, что на всем протяжении жизни этого поколения смертность в каждой возрастной группе будет оставаться неизменной на уровне расчетного периода.
Продолжительность предстоящей жизни рассчитывается для новорожденных (или иначе говорят — ожидаемая продолжительность жизни при рождении ) и для достигших некоторого возраста «х».
В виде формул расчет обеих средних можно представить следующим образом.
Для новорожденных:
 (6.5.9)
(6.5.9)
Поскольку при расчете средней продолжительности предстоящей жизни для новорожденных основание таблицы смертности l 0 = 1, его можно опустить, и окончательно этот показатель выражается в виде суммы чисел живущих в жизненном интервале от рождения поколения до его полного исчезновения.
Для людей, достигших определенного возраста « x », расчет отличается лишь тем, что число доживающих до возраста «х», в знаменателе дроби уже меньше 1 и его опускать нельзя.
 (6.5.10)
(6.5.10)
6.6. Расчет кратких таблиц смертности
Для анализа состояния и тенденций уровня смертности чаще всего бывает достаточным использование кратких таблиц смертности, т.е. по пятилетним возрастным интервалам. Для их построения необходимо располагать пятилетними возрастными коэффициентами смертности или данными для расчета таких коэффициентов. Обычно достаточно рассчитать лишь одну колонку таблиц, l x , q x или p x , а все остальные колонки, кроме L x , рассчитываются на основе взаимосвязей показателей таблиц смертности, представленных выше.
Для перехода от возрастных коэффициентов смертности т х к вероятностям смерти q x используется обычно одна из двух формул:
 (6.5.11)
(6.5.11)
 (6.5.12)
(6.5.12)
где q x — вероятность смерти в возрасте « х »; т х — возрастной коэффициент смертности; n — длина возрастного интервала.
Все остальные формулы показаны выше.
Построим для примера краткие таблицы смертности мужского населения России за 1995 г. и рассмотрим алгоритм расчета (см. таблицу 6.5).
1 . Из двух методов расчета по формулам (6.5.10) и (6.5.1 1) выберем второй метод — по показательной функции, потому, что она лучше, чем первая, учитывает кривизну изменения чисел доживающих l x . При этом вместо колонки вероятностей смерти q x будем рассчитывать колонку ее дополнения до единицы, т.е. вероятность дожития до следующего возраста, p x . Таким путем мы избежим большого числа вычитаний из единицы.
2. Но сначала нужно возрастные коэффициенты смертности разделить на 1000 (т.е. перевести их из промилле в доли единицы) и перемножить на длину соответствующих возрастных интервалов. Для первого возрастного интервала 0 лет множитель будет равен 1, для второго — 1 — 4 года — 4, для остальных интервалов — 5.
3. Затем, возводя основание натурального логарифма « е » в отрицательную степень, равную произведению возрастного коэффициента смертности на длину возрастного интервала, находим значения колонки вероятностей дожития p x (колонка 3 в таблице 6.5).
4. Следующая колонка — чисел доживающих « l x ». Первое значение числа доживающих для возраста 0 лет — основание таблицы смертности 100000 (константа, которую всегда нужно помнить). Умножив 100000 на число доживающих p 0 , получаем число доживающих l 1 , умножив l 1 на p 1 , получаем l 2 , и так — все значения колонки чисел доживающих до возраста «85 лет и старше».
5. Затем рассчитываем значения колонки d x как разность между соседними числами доживающих, т.е. 100000 – l 0 = d 0 ; l 1 – l 2 = d 1 , и т.д.
6. Далее рассчитываем числа живущих. Для всех возрастных интервалов, кроме первых двух ранних детских, числа живущих рассчитываются по формуле L x = dx / т х . Для первых двух возрастных интервалов — 0 и1—4 — числа живущих определяются иначе ввиду резкой кривизны изменения линии дожития на этом участке. Так число живущих в возрасте 0 лет определяется уравнением L 0 = l 0 - 2 / 3 d x . Число живущих в следующем детском возрастном интервале 1—4 года определяется из следующего уравнения 4 L 1 = 1,704 l 1 + 2,533 l 5 - 0,237 l 10 . Число живущих в так называемом открытом возрастном интервале — 85 лет и старше — определяется по формуле L 85+ = l 85 / m 85+ . Поскольку все дожившие до 85 лет раньше или позже умрут после этого возраста, d 85+ = l 85 .
Таблица 6.5
Расчет таблиц смертности мужского населения России в 1995 году
Возрастные группы (лет)
|
тx (в долях единицы) |
nmx/1000 |
px=exp(-nmx) |
lx |
dx |
А |
1 |
2 |
3 |
4 |
5 |
0 |
0,0205 |
0,0205 |
0,97971 |
100000 |
2029 |
1 — 4 |
0,0012 |
0,0048 |
0,99521 |
97971 |
469 |
5—9 |
0,0007 |
0,0035 |
0,99651 |
97502 |
341 |
10—14 |
0,0007 |
0,0035 |
0,99651 |
97,161 |
339 |
15—19 |
0,0024 |
0,0120 |
0,98807 |
96822 |
1155 |
20—24 |
0,0043 |
0,0215 |
0,97873 |
95667 |
2035 |
25—29 |
0,0054 |
0,0270 |
0,97336 |
93632 |
2494 |
30—34 |
0,0074 |
0,0370 |
0,96368 |
91138 |
3310 |
35—39 |
0,0100 |
0,0500 |
0,95123 |
87828 |
4283 |
40—44 |
0,0141 |
0,0705 |
0,93193 |
83545 |
5687 |
45—49 |
0,0193 |
0,0965 |
0,90801 |
77858 |
7162 |
50—54 |
0,0273 |
0,1365 |
0,87241 |
70696 |
9021 |
55—59 |
0,0340 |
0,170 |
0,84366 |
61675 |
9642 |
60—64 |
0,0471 |
0,2355 |
0,79018 |
52033 |
10917 |
65—69 |
0,0613 |
0,3065 |
0,73602 |
41116 |
10854 |
70—74 |
0,0779 |
0,3895 |
0,67740 |
30262 |
9763 |
75—79 |
0,1091 |
0,5455 |
0,57955 |
20499 |
8619 |
80—84 |
0,1555 |
0,7775 |
0,45955 |
11880 |
6420 |
85 и старше |
0,2252 |
|
|
5460 |
|
Таблицы 6.5 (продолжение)
Возрастные группы (лет)
|
Lx |
Tx |
ex |
exоф |
Разность
еx– еxоф |
А |
6 |
7 |
8 |
9 |
10 |
0 |
98647 |
5817496 |
58,17 |
58,27 |
- 0,10 |
1—4 |
390888 |
5718849 |
58,37 |
58,49 |
- 0,12 |
5—9 |
487143 |
5327961 |
54,64 |
54,78 |
- 0,14 |
10—14 |
484286 |
4840818 |
49,82 |
49,97 |
- 0,15 |
15—19 |
481250 |
4356532 |
45,00 |
45,12 |
- 0,12 |
20—24 |
473256 |
3875282 |
40,51 |
40,64 |
- 0,13 |
25—29 |
461852 |
3402026 |
36,33 |
36,48 |
- 0,15 |
30—34 |
447297 |
2940174 |
32,26 |
32,40 |
- 0,14 |
35—39 |
428300 |
2492877 |
28,38 |
28,51 |
- 0,13 |
40—44 |
403333 |
2064577 |
24,71 |
24,85 |
- 0,14 |
45—49 |
371088 |
1661244 |
21,34 |
21,47 |
- 0,13 |
50—54 |
330440 |
1290156 |
18,25 |
18,43 |
- 0,18 |
55—59 |
283588 |
959716 |
15,56 |
15,70 |
- 0,14 |
60—64 |
231783 |
676128 |
12,99 |
13,13 |
- 0,14 |
65—69 |
177064 |
444345 |
10,81 |
10,79 |
+0,02 |
70—74 |
125327 |
267281 |
8,83 |
8,74 |
+0,09 |
75—79 |
79001 |
141954 |
6,92 |
6,96 |
- 0,04 |
80—84 |
41286 |
62953 |
5,30 |
5,47 |
- 0,17 |
85 и старше |
21667 |
21667 |
3,97 |
4,23 |
- 0,26 |
7. Значения колонки чисел живущих в возрастах старше « x » - Т х — получаются суммированием чисел живущих L x с последовательным наращиванием суммы от конца ряда к началу.
8. Теперь путем деления чисел живущих в возрасте « х » лет и старше — T x — на соответствующие числа доживающих — l x — определяется средняя ожидаемая продолжительность предстоящей жизни — е x (колонка 8).
9. В колонке 9 показаны значения средней продолжительности жизни для всех возрастов, рассчитанные Госкомстатом России, а в колонке 10 — разность между значениями средней продолжительности жизни, рассчитанными нами по кратким таблицам смертности и сотрудниками госстатистики — по полным таблицам. Как видим, разница невелика, можно даже сказать — несущественна.
6.7. Уровень средней ожидаемой продолжительности жизни в России и его динамика
По данным Госкомстата России, средняя продолжительность жизни в стране в 1997 г. составила у мужчин 60,89 года, у женщин — 72,75 года. После резкого падения этого показателя в первой половине 90-х гг. — у мужчин почти на 6,2 года, у женщин — на 3,1 года, — в последние два года продолжительность жизни начала увеличиваться, и довольно быстро. Только затри года, 1995—1997, она увеличилась на 3,3 года у мужчин и на 1,6 года у женщин. Возможно, это не кратковременное колебание волны, а начало новой тенденции, свидетельство преодоления нашим народом шокового состояния и адаптации его к новым экономическим и социальным реалиям жизни. Но все же средняя продолжительность жизни нашего населения остается относительно низкой по сравнению с большинством экономически развитых стран и даже ряда развивающихся (см. таблицу 6.6).
В 1995 г. из 196 стран, по которым ООН рассчитывает среднюю продолжительность жизни (или получает данные из стран), Россия занимала 140-е место по продолжительности жизни мужчин и 100-е место — по продол жительности жизни женщин. Такое отставание нельзя оправдать никакими «объективными» причинами.
Таблица 6.6
Средняя ожидаемая продолжительность предстоящей жизни населения (для новорожденных) в России и отдельных странах мира в 1997 году
|
Страны
|
Коэффициент младенческой смертности, ‰ |
Средняя продолжительность жизни e0 |
Разность (лет)
|
Мужчины |
Женщины |
Россия |
17,2 |
60,89 |
72,75 |
11,86 |
Япония |
4,1 |
76,80 |
83,16 |
6,36 |
Швеция |
3,9 |
76,42 |
81,89 |
5,47 |
Израиль |
8,3 |
76,34 |
80,18 |
3,84 |
Франция |
5,8 |
74,44 |
82,53 |
8,09 |
Великобритания |
6,0 |
74,40 |
79,78 |
6,68 |
Германия |
5,3 |
73,64 |
80,16 |
6,52 |
Коста-Рика |
13,32 |
73,41 |
78,36 |
4,95 |
Тайвань |
6,7 |
73,28 |
79,30 |
6,02 |
Куба |
8,0 |
73,17 |
77,97 |
4,80 |
США |
6,6 |
72,25 |
79,49 |
6,74 |
Чили |
10,8 |
71,69 |
78,22 |
6,53 |
Аргентина |
19,7 |
70,67 |
78,12 |
7,45 |
Южная Корея |
8,0 |
70,01 |
77,69 |
7,68 |
Китай |
47,6 |
68,07 |
70,64 |
2,57 |
Вьетнам |
37,2 |
65,03 |
69,86 |
4,83 |
Индия |
65,5 |
61,68 |
63,18 |
1,50 |
Украина |
21,9 |
59,93 |
71,91 |
11,98 |
6.8. Средняя интервальная продолжительность предстоящей жизни
Средняя продолжительность жизни для новорожденных и для достигших любого возраста « х » является наилучшим показателем для характеристики уровня и динамики смертности. Ее главным достоинством является независимость от возрастной структуры населения. Однако и у нее есть недостаток. Она зависит от возрастной структуры самой смертности. К примеру, в 1997 г. средняя продолжительность жизни мужского населения в Латвии и Узбекистане была почти одинаковой, соответственно, 60,8 и 60,7 года. Но одновременно уровень младенческой смертности в Узбекистане почти в 4 раза превышал аналогичный уровень в Латвии (соответственно, 70,5 и 17,7). В то же время по таблицам смертности известно, что в старших возрастных группах уровень смертности в Узбекистане значительно ниже, чем в Латвии. То есть хотя средняя продолжительность жизни для новорожденных в целом мало различается в Латвии и Узбекистане, ее величина в разных возрастных группах может сильно различаться. Кроме того, величина средней продолжительности жизни для новорожденных в немалой степени зависит от того, как статистики определяют число живущих в самых старших возрастах. Поэтому представляется полезным рассчитывать так называемую интервальную продолжительность предстоящей жизни, т.е. продолжительность жизни в ограниченном снизу и сверху возрастном интервале. Такая продолжительность жизни зависит только от распределения чисел живущих в исследуемом возрастном интервале и не подвержена влиянию никаких других структурных факторов. Поэтому возможности сопоставимости такого показателя значительно лучше, чем обычной средней продолжительности жизни для новорожденных или для достигших некоторого возраста « x ».
Рассчитывается интервальная продолжительность жизни довольно просто, в двух вариантах: 1) для новорожденных и 2) для достигших некоторого возраста « х ».
Сначала посмотрим формулу в общем виде, для любого интервала:
 (6.8.1)
(6.8.1)
где x + n е х — средняя ожидаемая продолжительность предстоящей жизни в интервале « x + n »; Т х — число человеко-лет предстоящей жизни поколения в возрасте « х » и старше; Т х+п — число человеко-лет предстоящей жизни поколения в возрасте « x + n » и старше; п — длина возрастного интервала (может быть любым по произволу исследователя).
Иногда публикуются только три колонки таблиц смертности: l x , q x , и е х , по которым невозможно рассчитать колонки L x и Т х . Тогда можно определить Т х из соотношения e x = T s / l x , преобразовав его так: Т x = l x е х .
Теперь рассмотрим два вида формул интервальной продолжительности жизни, о которых говорилось выше, для новорожденных и для достигших возраста « x ». Отличие первой формулы от второй состоит лишь в знаменателе дроби формулы (6.8.1). При расчете интервальной продолжительности жизни для новорожденных в знаменателе показателя любых выделенных интервалов находится одно и то же число l 0 — основание таблицы. Поэтому показатели интервальной продолжительности жизни любых выделенных возрастных интервалов могут суммироваться и в итоге дают общую среднюю продолжительность жизни. Показатели же интервальной продолжительности жизни для достигших определенного возраста подобным свойством не обладают, поскольку у них в знаменателе дроби разные числа доживающих, числа доживающих до начала каждого возрастного интервала (с увеличением возраста эти числа последовательно уменьшаются). Посмотрим, как работает показатель средней интервальной продолжительности предстоящей жизни на примерах, выделив ряд возрастных интервалов.
Рассмотрим для примера динамику средней продолжительности жизни мужского населения СССР за десятилетие 1958—1970 гг. (см. таблицу 6.7).
Таблица 6.7
Средняя ожидаемая продолжительность жизни мужского населения СССР в отдельных возрастных интервалах в 1958—1959 и 1969—1970 гг.
Годы |
Всего ex
|
в том числе в возрастных интервалах (лет) |
0—14 |
15—29 |
30— 44 |
45—59 |
60—74 |
75 и ст. |
Для новорожденных
1958—1959 |
64,4 |
14,1 |
13,7 |
13,1 |
11,7 |
8,3 |
3,5 |
1969—1970 |
64,4 |
14,4 |
14,2 |
13,3 |
11,7 |
8,0 |
2,8 |
Разность |
0,0 |
+0,3 |
+0,5 |
+0,2 |
0,0 |
-0,3 |
-0,7 |
Для достигших начала каждого возрастного интервала
1958—1959 |
64,4 |
14,1 |
14,8 |
14,6 |
13,9 |
12,0 |
8,9 |
1969—1970 |
64,4 |
14,4 |
14,8 |
14,5 |
13,8 |
11,7 |
8,0 |
Разность |
0,0 |
+0,3 |
0,0 |
- 0,1 |
- 0,1 |
- 0,3 |
- 0,9 |
За указанное десятилетие средняя ожидаемая продолжительность предстоящей жизни для новорожденных мужчин в СССР вроде бы не изменилась. Как и 10 лет назад, она составляла 64,4 года (другое дело, хорошо ли это. Хорошо было бы, если бы она устойчиво росла). Однако дифференциация общей величины средней продолжительности жизни по возрастным интервалам обнаруживает противоречивую и не совсем благоприятную динамику средней продолжительности жизни. В младших возрастах она выросла, в старших — сократилась. Ее стабильность, вернее, стагнация, которая тоже признак негативный, оказывается на поверку иллюзорной, результатом двух противоположных процессов. В последующие годы сокращение средней продолжительности жизни постепенно передвигалось от старших возрастов к младшим, пока не охватило все возрастные группы. Если бы специалисты и властные структуры вовремя разглядели неблагоприятные симптомы снижения продолжительности жизни нашего народа, можно было бы своевременно начать разрабатывать меры социальной политики, направленные на преодоление нежелательных тенденций. Но время было упущено. Не только из-за безразличного отношения властей предержащих к этой стороне нашей жизни, но и по демографической неграмотности всего общества (правда, одно с другим тесно связано. Демографическая неграмотность и порождает равнодушие к демографической проблеме. Ее просто не замечают).
6.9. Показатели смертности по причинам смерти
Изучение структуры уровня смертности по причинам смерти — необходимое условие в исследовании факторов смертности. Причины смерти связаны с условиями жизни и труда людей, с их образом жизни. Изучая структуру смертности по причинам смерти можно установить роль тех или иных природных и социальных факторов, объективных и субъективных, зависящих и не зависящих от воли отдельного человека.
Для характеристики уровня смертности по причинам смерти используются два основных типа показателей: общие и возрастные коэффициенты. Общий коэффициент смертности по причинам смерти рассчитывается как отношение числа умерших от определенной причины смерти к средней для данного периода времени (обычно год) численности населения. Поскольку сумма чисел умерших от отдельных причин смерти, естественно, равняется общему числу умерших (от всех причин) и в знаменателе дроби при расчете общих коэффициентов смертности от отдельных причин смерти находится одна и та же численность населения, коэффициенты смертности по причинам смерти можно складывать. В итоге эта сумма равна общему коэффициенту смертности.
Ввиду того, что общие коэффициенты смертности, дифференцированные по множеству причин смерти, представляют собой очень малые числа, их выражают не в промилле, а в процентимилле (°/оооо), т.е. в расчете на сто тысяч человек. К сожалению, общие коэффициенты смертности по причинам смерти страдают теми же недостатками, что и не дифференцированные общие коэффициенты, т.е. зависят от различий возрастной структуры населения. Поэтому их необходимо стандартизовать, чтобы избавить от влияния особенностей возрастной структуры. В последние годы Госкомстат России в своих демографических ежегодниках начал регулярно публиковать стандартизованные общие коэффициенты смертности по причинам смерти, которыми и надлежит пользоваться.
Изменения структуры уровня смертности по причинам смерти в нашей стране за последние 30 лет показаны в таблице 6.8. Показатели в таблице стандартизованы по возрастной структуре населения Госкомстатом России (прямым методом), так что они сопоставимы и по полу, и в динамике.
Таблица 6.8
Структура смертности по причинам смерти в России (стандартизованные коэффициенты смертности по основным классам причин смерти и их удельный вес в процентах к общему коэффициенту, записанному в процентимилле)
Основные классы причин смерти
|
Коэффициенты (на 100 000 жителей соответствующего пола) |
Удельный вес умерших от данного класса причин смерти в общем числе умерших (в процентах) |
1965 |
1985 |
1995 |
1965 |
1990 |
1995 |
Мужчины
Всего умерших от всех причин |
1473,2 |
1807,9 |
2199,0 |
100,0 |
100,0 |
100,0 |
в том числе от: |
|
|
|
|
|
|
болезней системы кровообращения |
648,5 |
950,7 |
1051,8 |
44,0 |
52,6 |
47,8 |
Новообразований |
292,3 |
299,5 |
309,1 |
19,9 |
16,6 |
14,1 |
несчастных случаев, отравлений и травм |
180,0 |
239,6 |
394,7 |
12,2 |
13,2 |
18,0 |
болезней органов, дыхания |
136,0 |
157,3 |
142,2 |
9,2 |
8,7 |
6,5 |
болезней органов пищеварения |
42,1 |
50,7 |
68,8 |
2,9 |
2,8 |
3,1 |
инфекционных и паразитарных болезней |
69,7 |
30,5 |
38,0 |
4,7 |
1,7 |
1,7 |
всех прочих |
104,6 |
79,6 |
194,4 |
7,1 |
4,4 |
8,8 |
Женщины
Всего умерших от всех причин |
889,4 |
966,3 |
1060,9 |
100,0 |
100,0 |
100,0 |
в том числе от: |
|
|
|
|
|
|
болезней системы кровообращения |
504,4 |
634,0 |
633,2 |
56,7 |
65,6 |
59,7 |
Новообразований |
160,8 |
136,9 |
142,3 |
18,1 |
14,2 |
13,4 |
несчастных случаев, отравлений, и травм |
41,4 |
60,8 |
93,6 |
4,7 |
6,3 |
8,8 |
болезней органов дыхания |
63,5 |
55,2 |
37,5 |
7,1 |
5,7 |
3,5 |
болезней органов пищеварения |
21,7 |
22,5 |
30,7 |
2,4 |
2,3 |
2,9 |
инфекционных и паразитарных болезней |
21,9 |
9,0 |
8,4 |
2,5 |
0,9 |
0,8 |
всех прочих |
75,7 |
47,9 |
115,2 |
8,5 |
5,0 |
10,9 |
Если проследить динамику общего коэффициента смертности по Демографическому ежегоднику
[7], где представлены сплошные динамические ряды коэффициентов смертности по причинам смерти, откуда и заимствованы данные таблицы 6.8, то можно увидеть, что уровень смертности в стране в 1965—1984 гг. Медленно увеличивался и у мужчин, и у женщин, затем немного снизился на короткое время в 1985—1987 гг., что в определенной степени связано с печально знаменитой лихой лигачевской антиалкогольной кампанией
[8], а затем снова стал расти. В первой половине 1990-х гг. этот рост резко увеличился. И вновь, так же как и после антиалкогольной кампании 1985 года, только с обратным знаком, это повышение — вовсе не прямой результат социально-экономических реформ в нашей стране самих по себе (как это изображают коммунисты и их сторонники), а результат «адаптационного синдрома», психологической растерянности большинства народа, оказавшегося в непривычной и неожиданной ситуации. В 1995—1997 гг. смертность начала снижаться. Думается, это начало новой, положительной тенденции, в которой государственные меры играют определенную, но, возможно, не главную роль. Народ спасает себя сам.
Но вернемся к таблице 6.8 и рассмотрим изменение структуры смертности по причинам смерти. Обращает на себя внимание то, что 80% всей смертности у мужчин и 82% у женщин приходится всего на три класса причин смерти из 17 [9]. Это болезни системы кровообращения, новообразования, несчастные случаи, отравления и травмы. Следует заметить, что все эти причины в большой степени носят «поведенческий» характер, обусловлены в значительной степени образом жизни людей, отношением людей к своему здоровью, их самосохранительным поведением (о нем чуть позже). Здоровье и продолжительность жизни все в большей степени по сравнению с прошлыми эпохами начинает зависеть от воли и усилий само го человека, отдельной личности. Поэтому возрастает роль общественных наук, в частности социологии и психологии, особенно социальной психологии, в борьбе за увеличение средней продолжительности жизни народа. Чтобы оценить остроту проблемы уровня смертности и продолжительности жизни населения в нашей стране,
Таблица 6.9
Стандартизованные по возрасту показатели смертности по причинам смерти в России и США в 1992 г. (число умерших на 100 000 жителей) [10]
Причины смерти
|
Мужчины |
Женщины |
Россия
|
США
|
Индекс Россия США |
Россия
|
США
|
Индекс Россия США |
Число умерших от всех причин |
1803,7 |
998,8 |
1,806 |
918,5 |
612,5 |
1,500 |
В том числе от: |
|
|
|
|
|
|
болезней сердца |
481,5 |
325,7 |
1,478 |
257,2 |
191,5 |
1,343 |
поражений сосудов мозга |
288,3 |
51,2 |
5,631 |
225,3 |
45,4 |
4,963 |
злокачественных новообразований |
309,4 |
248,9 |
1,243 |
138,3 |
163,5 |
0,846 |
В том числе от: |
|
|
|
|
|
|
новообразований органов дыхания |
116,6 |
87,1 |
1,339 |
11,7 |
39,1 |
0,299 |
новообразований молочной железы |
— |
— |
— |
21,0 |
30,6 |
0,686 |
пневмонии и гриппа |
15,8 |
32,4 |
0,488 |
4,2 |
20,0 |
0,210 |
Хронических болезней печени и цирроза |
25,8 |
15,1 |
1,709 |
13,9 |
6,4 |
2,172 |
дорожных и недорожных мототранспортных несчастных случаев |
40,8 |
22,1 |
1,846 |
10,5 |
9,6 |
1,094 |
самоубийств и самоповреждений |
55,8 |
19,9 |
2,804 |
10,9 |
4,6 |
2,370 |
убийств и повреждений, преднамеренно нанесенных другими лицами |
36,4 |
15,3 |
2,379 |
9,7 |
4,0 |
2,425 |
Других внешних причин |
159,2 |
24,9 |
6,394 |
36,8 |
9,6 |
3,833 |
всех прочих причин |
390,7 |
243,3 |
1,606 |
211,7 |
157,9 |
1,341 |
представляется полезным сравнить показатели смертности по причинам смерти (конечно же, стандартизованные по возрасту) нашей страны с аналогичными показателями какой-ни будь другой страны, хотя бы такой, как США, в которой эти показатели далеко не самые лучшие в мире. Но лучше, чем у нас (см. таблицу 6.9).
В целом уровень смертности в 1992 г. (думается, что данные таблицы 6.9 не перестали быть актуальными за «давностью» лет) в России был выше, чем в США в 1,8 раза у мужчин и в полтора раза — у женщин. От большинства причин уровень смертности в России также намного выше, чем в США. Особенно значительна разница в смертности от сосудистых поражений мозга. Наши мужчины умирают от этой причины в 5,6 раза чаще, чем американцы, женщины — в 5,0 раз. От болезней сердца наши мужчины умирают чаще, чем в США в 1,5 раза, женщины — в 1,3 раза, от хронических болезней печени и цирроза — соответственно в 1,7 и 2,2 раза (какую-то роль здесь играют и злоупотребления алкоголем), от самоубийств — в 2,8 и 2,4 раза, от убийств — одинаково в 2,4 раза и у мужчин, и у женщин, от несчастных случаев, связанных с мототранспортом — в 1,8, но «всего» на 9,4% выше у женщин.
В то же время по некоторым причинам смерти наши данные выглядят более благополучно, чем американские. Так, смертность мужчин от пневмонии и гриппа у нас ниже, чем в США вдвое, а женщин — даже в 5 раз (что, вероятно, свидетельствует о способностях нашей массовой медицины эффективно бороться с эпидемиями). Смертность наших женщин от рака молочной железы ниже, чем в США, на треть, что также, возможно, является результатом профилактических мероприятий нашей медицины. Смертность от злокачественных новообразований органов дыхания у наших мужчин выше, чем в США в 1,4 раза, но у женщин, напротив, ниже втрое, чем в США. Объяснений этому последнему замечательному феномену мне пока не удалось найти.
Наилучшую характеристику смертности дают возрастные коэффициенты смертности по причинам смерти. В принципе они рассчитываются так же, как и общие коэффициенты, но в пределах каждой отдельной возрастной группы.
На базе возрастных коэффициентов смертности по причинам смерти строятся вероятностные таблицы смертности по причинам смерти, которые используются как для анализа состояния и динамики уровня смертности и продолжительности жизни, так и для ее прогноза. Таблицы смертности по причинам смерти позволяют получить представление о том, насколько средняя продолжительность предстоящей жизни изменяется в результате изменения уровня смертности от определенной причины смерти или класса причин.
6.10. Социальный прогресс и изменение структуры уровня смертности по причинам смерти
В течение тысячелетий человечество страдало и умирало от эпидемических Инфекционных заболеваний — чумы, холеры, оспы и других, опустошавших иногда целые страны. После промышленной революции, с началом второй фазы демографического перехода улучшаются экономические и санитарные условия жизни населения, начинается снижение уровня смертности и одновременно изменяется ее структура по причинам смерти. Массовые инфекционные заболевания отступают, их доля в структуре смертности снижается до минимума, а их место занимают неинфекционные хронические болезни, несчастные случаи и травмы. Возрастает роль профилактики здоровья, санитарных аспектов условий жизни и труда, возможности каждого отдельного человека сохранить свое здоровье или хотя бы отдалить приближение смерти. Отсюда возрастает роль социальных наук в изучении поведенческих аспектов смертности и продолжительности жизни, в выработке рекомендаций по развитию здорового образа жизни.
6.11. Факторы уровня смертности и средней продолжительности жизни
На уровень смертности и продолжительности жизни населения оказывает влияние множество природных и социальных факторов. При этом нужно подчеркнуть, что природные факторы со времени возникновения человеческого общества, производства и культуры не доминируют над человечеством, так сказать, в «чистом виде», они опосредуются, изменяются социальными условиями. Человечество давно уже живет в природно-социальной среде, И его судьба во все большей степени зависит от его выбора.
Все основные факторы представляется целесообразным, с известной степенью условности, объединить в четыре группы (перечисленные в порядке их значимости: 1) уровень жизни народа; 2) эффективность служб здравоохранения; 3) санитарная культура общества; 4) экологическая среда.
1. Уровень жизни народа. Уровень жизни представляется мне главным фактором улучшения здоровья населения, снижения уровня смертности и роста средней продолжительности жизни, потому что именно он создает условия (пространство) для развития всех остальных факторов роста общей и санитарной культуры, заботы о здоровье, для улучшения окружающей среды и т.д. Бедность всему этому никак не способствует. Между тем подавляющее большинство нашего населения — бедное по современным («западным») стандартам уровня жизни. К сожалению, мы толком не знаем, какой у нас уровень жизни и какими показателями его следует измерять. Советская социальная статистика для этой цели совершенно не пригодна, она насквозь лжива, и к тому же была почти полностью засекречена [11]. Однако по многим фрагментарным данным все же можно составить некоторое представление о том, что уровень жизни в нашей стране на протяжении десятков лет был крайне низким, на грани лишь простого воспроизводства личности человека и его рабочей силы или даже ниже. Развитие же личности происходило во многом за счет отказа от самого необходимого, в том числе от отдыха, от приобретения эффективных медикаментов и платных услуг здравоохранения, от качественного питания и проч.
Одним из наиболее совершенных комплексных показателей, с помощью которого оценивается на международном уровне уровень и качество жизни, является так называемый «индекс развития человеческого потенциала» (или «индекс человеческого развития»), который представляет собой среднюю арифметическую величину из показателя валового внутреннего продукта на душу населения, уровня образования населения и средней продолжительности предстоящей жизни. Что касается душевого валового внутреннего продукта, то этот показатель может давать неправильное представление об уровне жизни, если не раскрываются статьи его расходов. В советских, да и в постсоветских условиях сверхсекретности значительная часть внутреннего продукта тратится государством на огромные военные расходы, которые, однако, частично распределяются в бюджете по «мирным» статьям. То есть в наш уровень жизни могут входить и расходы на пушки вместо масла, и финансирование космических исследований, и т. п. Тем не менее, согласно данным Второго российского доклада (1996 г.), посвященного оценке уровня жизни в нашей стране и представленного в ООН, Россия по этому показателю в 1993 г. заняла 57-е место среди 174 стран мира [12], по которым этот индекс рассчитывается. В 1995 г. наша страна среди тех же 174 стран мира отодвинулась уже на 119 место [13]. Если учесть, что в мире насчитывается примерно 35 экономически развитых стран, то даже с учетом, вероятнее всего, завышенной оценки уровня жизни, даваемой индексом ИРЧП, наша страна находится далеко за чертой, отделяющей экономически развитые страны от «развивающихся» (точнее, отсталых). Дополнительно к этому можно сравнить уровень жизни в России и США по величине среднедушевого дохода в 1995 году. В США он оказывается выше, чем в России, в почти в 15 раз [14].
2. Эффективность здравоохранения. Если заглянуть в отечественный статистический справочник, увидим, что развитие нашего здравоохранения во все годы советской власти характеризовалось в основном показателями численности врачей и больничных коек, а также распределением их по специальностям и назначению. Вероятно, наше здравоохранение — единственная отрасль народного хозяйства или, во всяком случае, одна из немногих, деятельность которой оценивается не результатами, а затратами труда. По численности врачей и больничных коек мы давно уже «впереди планеты всей». Однако относительно низкий уровень и неблагоприятная динамика средней продолжительности жизни свидетельствуют о неэффективности здравоохранения. И это неудивительно, поскольку наше здравоохранение — в прямом смысле бедное, десятилетиями оно содержится на голодном финансовом пайке у государства. Во всех экономически развитых странах на здравоохранение расходуются значительные средства из государственного бюджета, которые постоянно возрастают. Так, уже к 1990 г. в большинстве экономически развитых стран расходы на здравоохранение превышали 8% от валового внутреннего продукта. В России же в это время они составляли всего 3,3% [15]. Причем примерно на таком же уровне эти расходы были и в бывшем СССР.
Составной частью проблемы низкого финансирования здравоохранения является очень низкая заработная плата занятых в этой отрасли. По данным за 1996 г. среднемесячная заработная плата работников здравоохранения, физической культуры и социального обеспечения (трудно объяснить обоснованность такого смешения) составляла 77% от аналогичной зарплаты в среднем по экономике страны. Ниже, чем в здравоохранении, заработная плата лишь у занятых в образовании, культуре и искусстве [16]. Тоже, кстати, чрезвычайно показательный симптом отношения нашего государства к самым жизненно важным для него, для государства, отраслям народного хозяйства. Вряд ли можно всерьез ожидать большого стремления врача к постоянному повышению своей квалификации при такой «нижайшей из низших» зарплате.
Вероятно, не меньшее значение, чем финансовое обеспечение здравоохранения, имеют его взаимоотношения с пациентом. В этом отношении организация нашего здравоохранения вряд ли значительно изменилась за последние 100 лет. По-прежнему она носит безличностный характер, т.е. врач в лечебном процессе не учитывает индивидуальности пациента, особенностей его личности, рассматривает его как неодушевленный организм (растение). Такой подход в большой степени был оправданным в эпохи до начала демографического перехода, когда в структуре уровня смертности по причинам смерти преобладали инфекционные эпидемии, поражавшие людей без различия их социальных и индивидуальных свойств. Но теперь он совершенно неэффективен.
В постпереходный период, когда в структуре смертности по причинам смерти происходят кардинальные изменения, когда начинают преобладать хронические, в значительной степени индивидуализированные заболевания, медицина, вернее, здравоохранение также должно меняться в сторону большего учета характера пациента и особенностей его уникальной судьбы. Требуется установление более долговременных, более личностных взаимоотношений между врачом и пациентом. Для этого необходимо разорвать крепостную приписку населения к районным поликлиникам, дать возможность гражданам выбирать для себя врача, которому они могли бы доверять. Введенная в нашей стране несколько лет назад система обязательного медицинского страхования, казалось бы, вполне может обеспечить возможность подобного выбора, а заодно и объективной оценки врачебной квалификации. Но, по всей видимости, такой функции эта система не выполняет. Она вновь являет собой бюрократическую процедуру. Лишь добавила гражданам заботы по периодическому переоформлению страховых полисов и необходимости не забывать брать их с собой, направляясь на прием к врачу.
В последние годы, по мере развития рыночных отношений в стране, расширяется платная кооперативная и частная медицина, которая в целом лучше относится к человеку, чем медицина казенная. Но... у наших людей в массе своей нет достаточных денег для того, чтобы пользоваться благами платной медицины. Виной тому нищенская заработная плата. Государство должно вернуть хотя бы часть денег, изымаемых из заработной платы трудящихся на «бесплатное» здравоохранение с тем, чтобы люди сами могли ими распорядиться.
3. Санитарная культура. Одним из важнейших социальных последствий изменения структуры смертности по причинам смерти является растущее значение санитарной культуры как одного из важнейших факторов поддержания здоровья и роста продолжительности жизни населения.
Коммунистический режим вопреки его внешне действительно прекрасным лозунгам оказался на деле антигуманным и бесчеловечным по отношению к большинству народа. Строительство нового общества осуществлялось многие десятилетия штурмовыми методами, на пределе напряжения сил. От людей требовалась самоотверженность и самоотречение ради осуществления идеи, отказ от жизни сегодняшней во имя жизни завтрашней, жизни для будущих поколений. В пропагандистском искусстве прославлялись нарушения норм техники безопасности, сверхурочный труд — все для того, чтобы сократить сроки производства, увеличить выработку. Результатами были низкое качество продукции, высокий травматизм и поломки оборудования, гибель людей и утрата здоровья. Была реально создана новая трудовая этика, в которой жизнь человека ценилась ниже машины. Подвиг из исключительного поступка был возведен в норму жизни, за соблюдение которой многие люди и платили своей жизнью, а некоторые — жизнью других. И многое из этой этики продолжает и сегодня укорачивать нашу жизнь. Как верно замечает известный российский демограф Владимир Михайлович Школьников, «российскому обществу и советского, и постсоветского периода была (и остается до сих пор) свойственна глубоко деформированная система ценностей, в которой ценности здоровья и жизни отдельного человека занимают слишком незначительное место, чтобы они способны были мобилизовать необходимые экономические ресурсы и социальную энергию на свою защиту» [17].
Низкая культура потребления алкоголя, массовое курение, в том числе распространенное среди женщин и подростков, огромное число искусственных абортов вместо современных средств контрацепции, повсеместная грубость в отношениях между людьми, сквернословие, разнузданность молодежи, пропаганда секса, насилия и жестокости средствами массовой информации — все это важнейшие факторы, разрушающие здоровье нации и не способствующие росту средней продолжительности жизни (а также укреплению семьи и росту рождаемости).
4. Качество окружающей среды. Здесь тоже немало проблем, которые теперь уже достаточно хорошо известны (хотя почти каждый день мы узнаем о новых, вернее, старых экологических бедах, но долгое время тщательно скрываемых). Почти все они — следствие гипертрофированной военной экономики советского государства, в которой вопросам охраны окружающей среды уделялось мало внимания (как и здравоохранению, жизненному уровню народа и всем остальным жизненно важным аспектам). По данным сети мониторинга загрязнения воздуха в городах Российской Федерации, функционирующего уже около трех десятилетий, загрязнение атмосферы промышленными отходами наблюдается почти во всех крупнейших промышленных городах России (различается лишь степень загрязнения, которая, однако, всюду превышает предельно допустимые концентрации — ПДК). Концентрации вредных веществ в атмосфере превышают допустимые пределы в 5 раз в 150 городах России, в 10 раз — в 86 городах [18]. По данным экологов, около половины населения России продолжают использовать для питья воду, не соответствующую гигиеническим требованиям по широкому спектру показателей качества воды. Почти все водоемы вблизи городов в той или иной степени загрязнены промышленными отходами в опасной для жизни и здоровья людей концентрации. Централизованным водоснабжением до сих пор пользуются лишь 68% сельских жителей России (47% населенных пунктов) [19].
Можно привести еще немало других данных, свидетельствующих о плохом состоянии окружающей среды в России, но, думается, и этих достаточно, чтобы иметь представление о том «вкладе», который экология вносит в нашу смертность.
6.12. Самосохранительное поведение
Возрастающая роль поведенческих аспектов в борьбе за продолжительность жизни нашла свое выражение и в исследовании факторов смертности и здоровья населения социологическими методами. По аналогии с определением репродуктивного поведения Самосохранительное поведение определяется как система действий и установок личности, направленных на сохранение здоровья и продление жизни.
Впервые в нашей стране пилотажные исследования самосохранительного поведения начала проводить небольшая группа социологов и демографов под руководством проф. А.И. Антонова, сначала в Центре по изучению проблем народонаселения (на экономическом факультете МГУ им. М.В. Ломоносова) в 1980—1983 гг., затем в Институте социологии АН СССР, в 1984—86 гг. (соответственно в другом составе исследовательской группы). Исследования проводились в Вильнюсе, Шауляе, Львове, Черновцах и других городах СССР. Всего было опрошено около 1500 человек, мужчин и женщин, среди которых люди моложе 30 лет составили 61%, а старше 50 лет — 13%. Более половины всех опрошенных составляли люди умственного труда. В качестве основных характеристик психологических установок к длительности жизни исследователи использовали фактически те же три показателя предпочтений, что и при изучении репродуктивного поведения, естественно в преломлении к актуальному предмету исследования: среднее идеальное, желаемое и ожидаемое число лет жизни. Ответы респондентов на вопрос об идеальной продолжительности жизни: «Какова, по вашему мнению, наилучшая продолжительность жизни?» — интерпретировались исследователями как характеристика представлений опрашиваемых о наилучших сроках жизни людей вообще, каких-то других людей, а не их лично. Ответы о желаемой продолжительности жизни: «Если бы у вас была возможность выбора, то какое число лет жизни вы предпочли бы для себя при самых благоприятных условиях?» — трактовались как потребность в длительности жизни, желание жить. Наконец, ответ на вопрос об ожидаемой продолжительности жизни: «Как вы думаете, до какого примерно возраста вам удастся дожить?» — интерпретировался в качестве характеристики представлений респондентов о сроках жизни, которых можно достичь в реальных обстоятельствах их жизни [20]. Все индикаторы предпочтений и ожиданий в отношении продолжительности жизни сопоставлялись с различными характеристиками респондентов. Было обнаружено, что мужчины в целом более пессимистично, чем женщины, оценивают свое здоровье. Как «хорошее» его оценили лишь 30% опрошенных мужчин в сравнении с 48% женщин, а доля тех, кто оценил свое здоровье как «плохое», среди мужчин оказалась в 2,5 раза больше, чем среди женщин. При этом из всех факторов, в наибольшей степени влияющих на здоровье, у мужчин на первом месте оказались «условия жизни» (41%), а важность «усилий самого человека» в достижении хорошего здоровья отметили лишь 29%. У женщин такие мнения составили соответственно 28 и 39% [21]. Таким образом, женщины проявили более активную позицию по отношению к сохранению здоровья.
Исследования также выявили значительную часть людей, по мнению которых не стоит стремиться жить как можно дольше. Эта часть не так уж мала, по данным упомянутых исследований она составляет около 25%. Такая позиция мотивируется боязнью остаться беспомощным и одиноким в старости и болезни. Различие жизненных позиций нашло свое отражение и в показателях предпочтения лет жизни. У «пессимистов» (если можно их так, исключительно условно, назвать) желаемая продолжительность жизни (сколько лет хотелось бы прожить при самых благоприятных условиях) составила 68,6 года сравнительно с 81,1 года по ответам «оптимистов», которые хотят жить дольше с тем, чтобы как можно больше в жизни испытать и как можно дольше не расставаться со своими близкими. Ожидаемая продолжительность жизни (до какого возраста вам удастся дожить) у первых составила 61,6 года, у вторых — 69,4 года. Внимание к сохранению своего здоровья также отражается в самосохранительных установках. Заботящиеся о своем здоровье ожидают прожить 79 лет, не заботящиеся — 71 год [22].
К сожалению, исследования самосохранительного поведения были прерваны очень скоро после своего начала. Они не получили поддержки ни со стороны руководства учреждений, в которых проводились, ни со стороны научного сообщества. Возможно, и сам А.И. Антонов утратил интерес к этой теме. Между тем ее вовсе нельзя считать исчерпанной или не представляющей научного интереса. По мнению того же А.И. Антонова, «остаются до сих пор неразработанными вопросы структуры самосохранительного поведения личности, взаимосвязи ее элементов, классификации основных результатов такого поведения (позитивных и негативных с точки зрения здоровья), вопросы взаимосвязи результатов самосохранительного поведения индивидов с состоянием здоровья, заболеваемости и продолжительности жизни различных групп населения, народонаселения страны в целом. Сегодня можно лишь говорить о постановке этой проблемы в рамках социологической демографии и социологии здоровья, поскольку в отдельных дисциплинах, и прежде всего в психологии, имеются разрозненные попытки по измерению субъективной продолжительности жизни, т.е. того числа лет, которое собирается, надеется прожить опрашиваемый человек». Остается надеяться, или даже, пожалуй, можно быть уверенным, что эта тема исследований еще найдет своих энтузиастов.
Рассчитывают возрастные коэффициенты смертности и для населения в целом (обоих полов). Но такие «гермафродитные» показатели имеют очень ограниченное применение, поскольку смертность сильно различается по полу и своими причинами, и своей интенсивностью.
[1] Демографический ежегодник России. 1998. — М., 1998. С. 253.
[2] Андреев Е.М. Младенческая смертность в России //Вопросы статистики. М., 1995. № 5. С. 66.
[3] Перинатальный период (от греч. peri — около, вокруг и лат. natalis —относящийся к рождению, вокруг родов) начинается с 28-й недели беременности, включает период родов и первые 7 суток жизни новорожденного (Народонаселение: энциклопедический словарь. — М., 1994. С. 316).
[4] Можно было бы «продолжить традицию» и показать использование косвенного метода стандартизации на примере динамики уровня смертности в России в 1990—1995 гг., который уже использовался для демонстрации индексного метода и прямого метода стандартизации коэффициентов. Но мы ограничимся тем, что я сообщу результат произведенного мною расчета, который, естественно, мало отличается от результата, полученного с помощью прямого метода стандартизации. Напомню, что с помощью прямого метода стандартизации мы установили, что за 1990—1995 гг. уровень смертности в России возрос на 26,8%, а не на 33,9%, как можно судить по фактическим коэффициентам. С помощью косвенного метода мы получаем рост уровня смертности на 30,1%. Разницу в результатах можно объяснить грубостью расчетов, различиями в округлениях цифр.
[5] В обыденном языке, а также и на профессиональном жаргоне этот показатель часто называется сокращенно — «средняя продолжительность жизни» или даже просто «продолжительность жизни». Возможно, такое сокращение можно признать допустимым, если при этом иметь правильное представление о сути показателя.
[6] Демографический ежегодник России. 1996. — М., 1996. С. 353—354.
[7] Автор отнюдь не защищает нашего общенационального пьянства, однако присоединяется к мнению многих специалистов, считающих кавалерийскую атаку «старых партийных товарищей» на алкоголь неразумной и безуспешной акцией. Бороться надо не с алкоголем, а с алкоголизацией, бороться долго и научно. Временное сокращение уровня смертности в 1985—1987 гг. было результатом «адаптационного синдрома», т.е. некоторого психологического замешательства населения, застигнутого запретом на алкоголь врасплох, а вовсе не запрещения самого по себе. Пока народ привыкал к новой ситуации, он вынужден был ограничить потребление спиртного. Но он быстро приспособился, увеличил производство самогона и суррогатов, потянулся к наркотикам и химикатам, и смертность вновь начала расти. Ничего другого нельзя было ожидать.
[8] Наименования классов причин смерти, принятых Госкомстатом России в соответствии с международной классификацией, см.: Демографический ежегодник России. 1996. — М., 1996. С. 308.
[9] Источник данных: Статистика здоровья и здравоохранения: Российская Федерация и Соединенные Штаты Америки, избранные годы 1980—1993 (с дополнительными данными по Российской Федерации на 1994 г.) // Статистика здоровья и здравоохранения. Серия 5. Международные статистические отчеты по здоровью и здравоохранению, № 9. М., декабрь 1995. С. 12—13.
[10] Показательно, что и статистические данные об уровне жизни населения в западных странах были возведены в ранг военных секретов — чтобы мы не знали, как можно жить.
[11] Иванов А. Бедность — не порог // Новое время. — М., 1997. № 25. 29 июня. С. 17.
[12] Жуков В.И. Потенциал человека: индекс социального развития // Семья в России. — М., 1996. № 1.С. 45.
[13] Рытов Ю. Средний класс – не для нас //Новое время. – М., 1996. № 22. май. С. 38.
[14] Школьников В.М. Здоровье населения России //Вопросы статистики. – М., 1997. № 3. С. 73.
[15] Социальное положение и уровень жизни населения России. 1997. – М.: Госкомстат России. 1997. С. 84.
[16] Школьников В.М. Здоровье населения России // Вопросы статистики. — М., 1997. № 3. С. 73.
[17] Безуглая Э.Ю. Загрязнение атмосферы городов //Атлас «Окружающая среда и здоровье населения России» /Под ред. Мюррэя Фешбаха. – М., 1995. С. 2 - 17.
[18] Бобров Ю.А. Использование и загрязнение вод // Атлас «Окружающая среда и здоровье населения России». — М., 1995. С. 2, 19, 20.
[19] Антонов А.И. Опыт исследования установок на здоровье и продолжительность жизни //Социальные проблемы здоровья и продолжительности жизни — М., 1989. С. 44 — 45.
[20] Журавлева И.В. Самосохранительное поведение и здоровье //Проблемы демографического развития СССР. — М., 1988. С. 111 —112.
[21] Антонов А.И. Самосохранительное поведение //Народонаселение: энциклопедический словарь. — М., 1994. С. 419.
[22]Антонов А.И. Опыт исследования установок на здоровье и продолжительность жизни // Социальные проблемы здоровья и продолжительности жизни. — М., 1989. С. 44.