Математическое приложение
Принципы экономической науки. Альфред Маршалл. Книга
шестая
Содержание
Математическое приложение. -
Замечание I
Закон уменьшения предельной полезности можно
выразить следующим образом. Если u -общая полезность товара для данного
лица, а х - ее величина, то предельная полезность измеряется (du / dx)
* бx , а (du / dx) измеряет предельную степень полезности.
Джевонс и некоторые другие авторы используют термин "конечная полезность" для
обозначения того, что в других местах Джевонс называет конечной степенью
полезности. Есть основания сомневаться, какое же из этих выражений более
обоснованно, поскольку на этот счет нет никаких указаний. С приведенным здесь
уточнениями (d2 u / dx2) всегда имеет отрицательное значение.
Математическое приложение. -
Замечание II
Если m — сумма денег или общей покупательной силы, которой располагает
данное лицо в какой-то момент, а р представляет общую полезность этой
суммы для него, то предельную полезность денег для данного субъекта определит
(dм / dm ).
Если р - цена, которую он еще согласен уплатить за х' товара,
доставляющего ему общее удовлетворение и, то
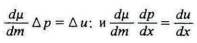
Если р' — цена, которую он еще согласен уплатить за х' другого
товара, доставляющего ему общее удовлетворение u' то
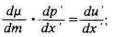
и поэтому
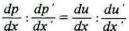
(ср. с выводами Джевонса в 'Theory of Exchange", p. 151.).
Каждое увеличение его средств уменьшает предельную степень полезности денег
для него, т. е. (d2м / dm2) всегда имеет отрицательное значение.
Следовательно, если предельная полезность для
него х товара останется неизменной, то прирост, его средств увеличит (du
/ dx) : (dм / dm), другими словами, увеличит (dp / dx), т.е.
норму, по которой он будет склонен платить за дальнейшее расширение потребления.
Мы можем считать (dp / dx) функцией m, и х, и тогда
получаем (d2p / dm dx ) всегда имеющее положительное значение.
Разумеется, и (d2p / du dx ) также всегда положительно.
Математическое приложение. -
Замечание III
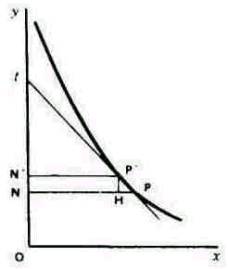
Пусть Р,Р' -точки пересечения кривой спроса и PRM
перпендикуляр, опущенный на Ох и пусть РР' пересекает Ох и
Оу в точках T и t соответственно. Тогда P'R -
приращение спроса, соответствующее снижению PR цены единицы товара. Тогда
эластичность спроса в точке Р измеряется (P'R1/OM) : (PR/PM), т.е.
(P'R/PR) x (PM/OM), т.е. (TM/PM) x (PM/OM), т.е. (TM/OM) x (PT/Pt)
или (PT/Pt)
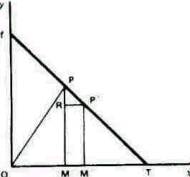
При неограниченном уменьшении расстояния между Р и Р' отрезок
РР' становится исчезающе малой величиной, и это доказывает утверждение,
высказанное в кн. III гл. 4. Априори очевидно, что при изменении масштабов
измерения отрезков, параллельных Ох и Оу, то отношению друг к
другу мера эластичности не меняется. И геометрически можно легко доказать этот
вывод методом проецирования, что же касается аналитических методов, то ясно, что
значение (dx/x) : (-dy/y) являющегося аналитическим выражением меры
эластичности, не изменяется, если кривая y=f(x) будет изображена в другом
масштабе, так как оно выражается теперь равенством qy =f(рх), где р
и q — константы.
Если эластичность единицы спроса будет одинакова при любой цене на товар, то
любое снижение цены вызовет пропорциональное увеличение суммы покупок и поэтому
не вызовет никаких изменений в совокупных расходах потребителей на этот товар.
Поэтому подобный спрос можно назвать спросом постоянных расходов. Кривая,
выражающая этот спрос, - так называемая кривая постоянных расходов - это
гипербола в прямоугольной системе координат, а Ох и Оу - ее
асимптоты. Семейство таких кривых изображено штриховыми линиями на следующем
рисунке.
Наши глаза уже немного привыкли к форме этих кривых, поэтому, взглянув на
кривую спроса, мы сразу можем определить, под большим или меньшим углом она
находится к вертикали, чем та часть кривой постоянных расходов, которая проходит
через эту точку. Более точно мы можем определить это, нанеся кривые постоянного
спроса на папиросную бумагу и наложив ее на кривую спроса. Используя это
средство, мы можем сразу увидеть, например, что на представленном рисунке во
всех точках кривой спроса - А, В, С и D эластичность
почти равна единице, на отрезках АВ и CD - больше единицы, а на
отрезке ВС — меньше единицы. С помощью этого приема легко проверить
допущения относительно характера спроса на товар, поскольку он заложен в кривой
спроса любой формы, и это предохранит нас от неосторожного введения невероятных
предпосылок.
Общее уравнение для кривой спроса, представляющее эластичность в любой ее
точке, равной n, имеет следующий вид:
( dx / x ) +
n*( dy / y )=0, т.е.
x y^n = C
Следует заметить, что в такой кривой ( dx /
dy ) = - c / ( y^n+1) , т. е. что пропорция, в которой возрастает суммарный
спрос в результате небольшого снижения цены, колеблется обратно ( n + 1)^th
показателя степени цены. Для кривых постоянного спроса она варьирует обратно
квадрату цены или - что в данном случае одно и то же — непосредственно квадрату
суммы [Т.е. обратно пропорционально квадрату суммы исходной цены и ее
прироста. - Прим. пер.].
Математическое приложение. -
Замечание IV
Если измерять промежуток времени вниз по оси Оу, а записываемые суммы
- расстоянием от Оу по оси Ох, то Р' и Р будут
смежными точками на кривой, показывающей увеличение суммы, а темп роста за
короткий период N'N будет равен
PH / P'H' = ( PH / P'H ) * ( P'H
/ P'H' ) = ( PN / Nt ) * ( P'H / P'N' ) = P'H / Nt
поскольку PN и P'N' в пределе равны.
Если за единицу времени мы возьмем год, то годовой темп роста будет обратен
числу лет на отрезке Nt. Если Nt равен с - константе для
всех точек кривой, темп будет постоянным и равным 1/c. В данном случае
-х * (dy / dx ) = с для всех значений х, т.е. уравнением кривой
является y = а - с logx.
Математическое приложение. -
Замечание V
Мы видели в тексте, что норма дисконтирования будущих удовольствий для разных
индивидов колеблется в широких пределах. Пусть r будет годовой нормой
процента, прибавляемой к настоящему удовольствию, чтобы приравнять его к
будущему; оно может быть равно 50 или даже 200% для одного человека и
отрицательной величиной для его соседа. Более того, одни удовольствия сильнее,
чем другие, и вполне возможно даже, что человек будет дисконтировать свои
будущие удовольствия самым оригинальным способом; он может оказаться склонным
отложить удовольствие с таким же успехом на два года, как и на один год,или
может сильно сопротивляться его откладыванию на продолжительный период и почти
вовсе не возражать против того, чтобы отложить его на короткое время. Существуют
определенные разногласия относительно частоты подобных отклонений, и вопрос этот
решить нелегко, так как, поскольку измерение удовольствий целиком субъективно,
его трудно проверить. В случае, когда такие отклонения исклю чены, норма
дисконтирования будет одинаковой для любой единицы времени, или, если выразить
это другими словами, она будет подчиняться закону экспоненциального роста. И
если будущую сумму удовольствия обозначить h, его вероятность - р,
время до его получения (если оно вообще придет) — t, и, если R = 1 + r,
тогда текущая оценка удовольствия будет равна p*h*R^(-t). Следует помнить
при этом, что полученный результат принадлежит гедонике, а не экономической
науке.
Продолжая анализировать эту гипотезу, мы можем сказать, что если w —
вероятность, что данному субъекту достанется элемент счастья ^h от
обладания, скажем, пианино на отрезке времени t , то стоимость пианино
для него в настоящем будет равна
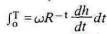
Если мы хотим учесть всю массу счастья для
данного случая за любой промежуток времени, мы должны принять T=°°. Если
источник счастья, по Бентаму, "низкий", dh / dt будет, вероятно,
отрицательной величиной для некоторых значений t, и, конечно же,
отрицательной будет вся интегральная сумма.
Математическое приложение. -
Замечание VI
Если у — цена, при которой х товара может найти покупателей на
данном рынке, и у = f (x) — уравнение для кривой спроса, тогда суммарная
полезность товара равна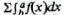 
, где а
— потребленное количество.
Если, следовательно, количество b товара необходимо для существования,
f (z) будет бесконечным или, по меньшей мере, неопределенно большим,
поскольку значения х меньше, чем b. Поэтому мы должны исключить
некоторое количество, необходимое для гарантирования жизни, и исчислить отдельно
суммарную полезность той части предложения товара, которая является избытком над
абсолютно необходимым количеством; она, конечно, равна
.
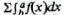Если существует несколько товаров, удовлетворяющих одну и ту же абсолютную
потребность, как, например, вода и молоко - и то и другое утоляет жажду,- то для
обычных условий жизни не будет большой ошибки, если мы условимся, что
необходимое потребление обеспечивается исключительно одним из них — самым
дешевым.
Как можно было заметить, анализируя
дополнительную выгоду потребителя, предельную полезность денег отдельного
потребителя мы предполагаем всегда неизменной. Строго говоря, мы должны принять
в расчет тот факт, что если он потратил меньше денег на чай, то предельная
полезность денег для него станет меньше и он сможет извлечь элемент
дополнительной выгоды потребителя из покупки других товаров по ценам, которые
сейчас не приносят ему такой ренты. Однако этими изменениями (второго порядка)
ренты потребителя можно пренебречь, исходя из предпосылки, на которой покоится
все наше доказательство, что его расходы на какой-то отдельный товар, например
на чай, составляют лишь незначительную часть его совокупных расходов. (Сравни с
§ 3 гл. III кн. V.) Если по каким-либо причинам нам понадобится принять в расчет
влияние его расходов на чай на стоимость денег для него, будет достаточно лишь
умножить f (x) в рамках приведённого выше интеграла на функцию x*f (x)
(т. е. суммы, уже затраченной им на чай), которая выражает предельную полезность
денег для него, когда общая их сумма сократилась на эту величину.
Математическое приложение. -
Замечание VII
Таким образом, если a1, a2, a3 ... —
потребленные количества товаров b1, b2, b3 ... необходимых для
существования, если у = f1 (x), у = f3 (x), у = f3 (x) -уравнения кривых
спроса для этих товаров и если мы абстрагируемся от любых неравенств в
распределении богатства, тогда общая полезность дохода, за вычетом той ее части,
которая гарантирует существование, может быть представлена как
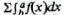условии, что
мы найдем способ объединить в одной общей кривой спроса все те товары, которые
удовлетворяют одну потребность и конкурируют друг с другом, а также
сгруппировать все товары, пред оставляющие взаимозаменяемые услуги (см. кн. V,
гл. VI). Однако мы не в состоянии это сделать, и поэтому формула остается просто
общим выражением, не имеющим практического значения. См. сноску в кн. III гл. 6,
а также последнюю часть примечания XIV.
Математическое приложение. -
Замечание VIII
Если у - счастье, которое приносит индивиду доход х, и если мы
предположим вслед за Бернулли, что при любой величине его дохода увеличение
счастья от прироста дохода на 1% одинаково, то мы полу чим х * ( dy /
dx ) = К и поэтому у =R log х + С, когда К и С —
константы.
Предположим далее вместе с Бернулли, что а — доход, обеспечивающий
необходимейшие средства существования: страдания превышают удовольствия,
когда доход меньше а, и уравновешивают их, когда он больше а.
Тогда наше уравнение принимает форму y =K log ( x / a). И К и а,
разумеется, варьируют в зависимости от темперамента, здоровья, привычек и
социального окружения каждого индивида. Лаплас назвал х физическим
счастьем, а у — духовным счастьем.
Сам Бернулли, по-видимому, считал, что х и а представляют
количества собственности, а не дохода, однако мы не можем оценить собственность,
необходимую для жизни, без определенного понимания продолжительности периода, в
течение которого она может обеспечить жизнь, т.е. без фактического представления
ее как дохода.
Догадка, которая привлекла наибольшее внимание
после Бернулли,— это, возможно, предположение Крамера о том, что удовольствие,
обеспечиваемое богатством, варьирует пропорционально квадратному корню величины
последнего.
Математическое приложение. -
Замечание IX
Доказательство того, что тотализатор — грубая экономическая ошибка, обычно
основывается на предположениях Бернулли или им подобных. Однако оно не требует
иных предпосылок, чем, во-первых, что удовольствием от азартных игр можно
пренебречь, и, во-вторых, что ф" (х) имеет отрицательную величину для
всех значений х, где ф(х) — удовольствие, получаемое от богатства,
равного х. Это можно объяснить следующим образом. Предположим, что
вероятность конкретного случая равна р и человек держит честное пари ру
против (1 —р)у, что этот случай произойдет. Поступая таким образом, он
изменяет свое ожидание счастья с ф(х) на р * ф( х + (1 — р) * у) + ( 1
— р ) * ф( х - р * у ).
Раскрыв это выражение согласно теореме Тейлора, получаем
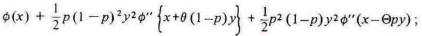
предполагая, что ф" (х) отрицательно для всех значений х,
приведенное выражение всегда меньше ф(х).
Конечно, эта потеря вероятного счастья не
обязательно должна быть больше, чем удовольствие, которое дает волнение азарта,
но мы должны вернуться тогда к тезису о том, что удовольствия от азартных игр
являются, по Бентаму, "низкими", поскольку, как показывает опыт, они могут
вырабатывать беспокойный, скверный характер, непригодный для постоянного труда,
равно как и для более высоких и серьезных жизнен ных наслаждений.
Математическое приложение. -
Замечание X
Следуя той же линии анализа, что и в замечании I, предположим, что v —
неполезность или бесполезность труда l , тогда dv / dl измеряет
предельную неполезность труда и согласно разъяснениям, приведенным в тексте,
(d^2 v) / (dl^2) положительно. Пусть m — сумма денег, или общей
покупательной силы, которой располагает данный человек, м — ее общая
полезность для него и поэтому dм/dm - ее предельная полезность. Отсюда
если ^w — заработная плата, которую необходимо заплатить, чтобы побудить
его выполнить работу ^l, то ^w * (dм / dm) = ^v и , ( dw / dl )
* ( dм /dm ) = dv / dl .
Если мы допустим, что его нежелание работать
выражается не фиксированной, а переменной величиной, то сможем считать dw/dl
функцией m, v и l, и тогда ( d^2 v) / (dm * dl) и ( d^2
v) / (dv * dl) всегда положительны.
Математическое приложение. -
Замечание XI
Если бы представители какого-либо вида птиц усвоили привычку жить на воде, то
любое увеличение перепонок между пальцами — то ли постепенное, в результате
естественного отбора, то ли вследствие внезапной флуктуации — будет
способствовать их жизни на воде и увеличивать вероятность того, что их потомство
будет в большей степени зависеть от роста перепонок. Поэтому если f (t) -
средняя площадь перепонок в момент t, то норма расширения площади
перепонок увеличивается (в определенных границах) с каждым увеличением числа
перепонок, значит f" (t) всегда положительно. Мы знаем теперь, что по
теореме Тейлора
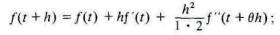
и если h велико, тогда h^2 -
очень велико и тогда f(t + h) будет намного больше, чем f(t), даже
если f(t) невелико (a f'"(t) никогда не принимает больших
значений) . Связь между результатами, полученными благодаря использованию
дифференциального исчисления в физике в конце XVIII в. и начале XIX в., и
развитием теории эволюции более чем поверхностна. Как и в биологии, в социологии
мы исследуем накопленные результаты действия факторов, которые, хотя вначале и
слабы, но набирают все большую силу от роста своих последствий, и теорема
Тейлора - универсальная форма, лишь конкретными выражениями которой являются
приведенные выше факты, другими словами, соответствующее выражение функции
нескольких переменных, когда требуется принять в расчет действие во времени
более чем одной причины. Этот вывод останется верным, даже если дальнейшие
исследования подтвердят сделанный некоторыми последователями Менделя вывод о
том, что постепенные изменения рода вызываются значительными отклонениями
отдельных особей от преобладающего типа, поскольку экономическая наука — это
изучение человечества, отдельных народов, тех или иных социальных слоев, которое
лишь косвенно затрагивает жизни людей исключительного таланта или исключительных
злобы и неистовства.
Математическое приложение. -
Замечание XII
Если, как в примечании X, v —
бесполезность данного количества труда, которое человеку предстоит затратить,
чтобы получить х товара, доставляющего ему удовольствие u, тогда
удовольствие от дальнейшего потребления этого товара будет равно страданию,
связанному с приобретением этого товара при (du/dx) = (dv/dx). Если
тягость труда понимать как отрицательное удовольствие, т.е. принять, что U= -v,
тогда (du/dx) + (dU/dx) =0, т. е. u + U = max в точке прекращения
труда.
Математическое приложение. -
Замечание XII bis
В статье, опубликованной Giornale degli Economisti в феврале 1891 г.,
проф. Эджуорт приводит показанную ниже диаграмму, на которой представлен случай
прямого обмена яблок на орехи, описанный в Приложении F . Количество яблок
измеряется по оси Ох, а орехов — по Оу. Ор = 4, pa =40,
а точка а представляет окончание первой сделки, в которой четыре яблока обменены
на 40 орехов. В данном случае преимущество вначале на стороне А (b
представляет вторую, а с — последнюю стадию случая). Точно так же а'
представляет первую, b' - вторую, с' — третью и d' —
последнюю стадии случая, в котором сначала выгоду получает сторона В.
QP— траектория, на которой должны обязательно лежать с и d'
проф. Эджуорт назвал ее кривой контракта.
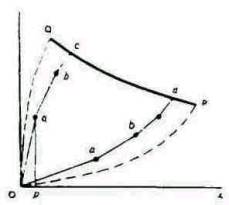
По методу, изложенному им в его "Математической физике" (1881), он
выражает через U общую полезность для A яблок и орехов в момент,
когда он уже отдал х яблок и получил у орехов через V — общую
полезность для В яблок и орехов в момент, когда тот уже получил х яблок и
отдал у орехов. Если дополнительные ^x яблок обмениваются на ^у
орехов, обмен безразличен для А, когда
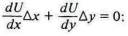и безразличен
для В, когда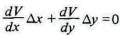 
Эти выражения представляют, таким образом, уравнения кривых безразличия ОР
и OQ, и кривая контракта, являющаяся геометрическим местом точек, в
которых условия обмена, безразличные для А, так же безразличны и для В,
выражается изящным уравнением
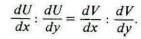
Если предельная полезность орехов постоянна для А, а также для В dU/dy
и dV/dy - константы, U становится ф(а - х) + а * у, V
становится Ш (а — х) + в * у и кривая контрактов становится F(x)
= О или х=С, т.е. прямой линией, параллельной Оу, а значение
^у : ^х, задаваемое каждой кривой безразличия, является функцией С.
Таким образом, мы видим, что, с какой бы траектории ни начинался бартерный
обмен, равновесие достигается в той точке, до которой доходит С по
яблокам, и конечная пропорция обмена является функцией С, т. е. также
константой. Это последнее приложение предложенной проф. Эджуэртом математической
версии теории бартерного обмена, которое приведено для подтверждения
результатов, содержащихся в тексте, было впервые разработано г-ном Берри и
опубликовано в Giomale degli Economisti в июне 1891 г.
Попытка проф. Эджуорта представить U и V как общие функции х
и у, очень привлекательна для математиков, но, кажется, менее пригодна
для отражения повседневных фактов экономической жизни, чем представление
предельных полезностей яблок функцией просто х, как делал Джевонс, В этом
случае, если А вначале вовсе не получает яблок, как предусматривается
анализируемым случаем, U принимает форму
равно как и V. Тогда уравнение кривой контракта принимает форму
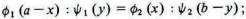
которая представляет собой одно из уравнений
обмена Джевонса ("Theory", 2nd Edition, p. 108).
Математическое приложение. -
Замечание XIII
Используя ту же нотацию, что и в Замечании V, возьмем в качестве отправной
точки во времени дату начала строительства дома и обозначим время строительства
Т. Тогда настоящее значение удовольствий, которые он ожидает от дома,
равно
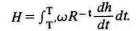
Пусть ^v - величина усилий, приложенных им к строительству дома за
время ^T (интервал между моментами t и t + ^t). Тогда
настоящая величина совокупных усилий равна
Если существует какая-либо неопределенность относительно количества труда,
которое пойдет на строительство, то каждая возможная часть учитываемого труда
должна быть помножена на вероятность его приложения w'; тогда V
принимает форму
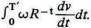
Если мы приведем отправную точку к дате завершения строительства дома, то
получим
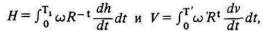
где T1 = T - T', и эта начальная точка, хотя она, возможно, менее
естественна с математической точки зрения, с точки зрения обыкновенного бизнеса
более естественна. Принимая ее, мы представляем V как измеренную
совокупность необходимых страданий вместе с бременем ожиданий, накопленных за
время от начала страданий до того момента, когда они начинают приносить плоды.
Не обязательно допущение, что представляемая
функция — первого порядка — наносит определенный ущерб анализу капиталовложений
у Джевонса, который еще заметнее, когда он сам, описывая работу Госсена,
выдвигает возражения против собственного намерения заменить многообразные
кривые, выражающие действительный характер колебаний экономических величин,
прямыми линиями.
Математическое приложение. -
Замечание XIV
Пусть а1, а2, а3,... - несколько количеств труда разных видов,
например лесоруба, каменщика, землекопа и т.д., выполняемого человеком на
строительстве дома, которое осуществляется по определенному плану; и в1,
в2, в3 и т.д.— несколько количеств различных удобств,
предоставляемых гостиными, спальнями, холлами и другими помещениями дома. Тогда,
используя V и H в том же значении, что и в предыдущем примечании,
V, в, в', в",- все являются функциями а1, а2,
а3,... и Н, будучи функцией в, в', в",...,
является также и функцией а1, а2, а3,.... Перед нами предельные
вложения труда каждого вида для каждого вида использования его результатов.
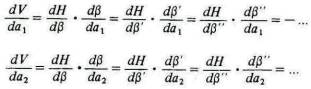
Эти уравнения представляют баланс затраченных усилий и полученных выгод.
Реальные издержки для него незначительные увеличения труда, затрачиваемого на
рубку леса и обработку древесины, в точности уравновешиваются дополнительными
удобствами, предоставляемыми ему гостиной или спальней благодаря этим затратам.
Если, следовательно, он вместо того, чтобы выполнять эту работу самому, заплатит
за нее плотнику, то V будет представлять не его общие усилия, а его
совокупные затраты общей покупательной силы. Тогда норма оплаты, которую он
будет склонен выделить на дополнительный труд плотника, измеряется dV/da
, тогда как dh/dв и dH/dв' будут для него денежными
мерами предельных полезностей услуг, дополнительно предоставляемых ему
соответственно гостиной и спальней, т. е. предельными ценами его спроса на эти
услуги, а dв/da и dв'/da выразят предельные
производительности труда плотника, обеспечивающего эти услуги. Тогда при
соответствующим образом подобранных единицах измерения приведенные выше
уравнения устанавливают, что цены спроса на труд плотника стремятся быть равными
ценам спроса на дополнительные удобства, предоставляемые гостиной и спальней,
помноженные в каждом случае на предельные производительности труда плотника,
обеспечивающего эти дополнительные удобства.
Если придать этому положению более общий вид, так, чтобы оно охватывало весь
колеблющийся спрос на рынке плотницкого труда, то его можно будет выразить в
следующей форме: цена спроса (предельная) на плотницкий труд равна
производительности (предельной) плотницкого труда, затраченного на расширение
предложения любых его продуктов, помноженной на цену спроса (предельного) на эти
продукты. Или, другими словами, оплата единицы плотницкого труда стремится быть
равной такой части любого из этих продуктов, в производстве которых требуется
труд плотника, которая представляет предельную производительность единицы
плотницкого труда в производстве этих продуктов; т. е. — используя выражения,
подробно рассмотренные в гл. I кн. VI, — она стремится быть равной стоимости
"чистого продукта" труда. Это положение очень важно и выражает самую суть
проблемы спроса в теории распределения.
Представим себе теперь строителя, задумавшего возвести определенные здания,
обеспечивающие различные удобства, например жилые дома, склады, заводские
корпуса и магазины розничной продажи. Вопросы, которые ему надо решить, делятся
на две группы: сколько удобств каждого рода он должен обеспечить и какими
средствами обеспечить эти удобства. Таким образом, кроме вопроса о самом
строительстве зданий, предоставляющих определенную сумму удобств, он должен
решить, какие факторы производства он будет использовать и в каком соотношении,
другими словами,использовать ему черепицу или шифер, сколько кирпича пойдет на
строительство, будет ли он использовать паровые машины только для подъемных
работ или также в приготовлении раствора и т.д.; и - если речь идет о
строительстве в крупном городе — использовать ему для строительства лесов
специалистов или обыкновенных рабочих и т.д.
Допустим, что он решил обеспечить в жилых удобств, в
' складских, в" — заводских услуг и т.д., каждое определенного
класса. А вместо предположения об использовании им просто а1, а2,...
количеств наемного труда, как ранее, разделим на группы его расходы, выделив
такие категории, как (1) заработная плата, (2) цены на сырье материалы, (3)
процент на капитал и (4) стоимость его собственных труда и предпринимательства.
Итак, пусть х1, х2,...— количества различных видов наемного труда,
включая труд по надзору, соответствующей продолжительности и интенсивности.
Пусть у1, у2,...— количества разного рода материалов, потребленных и
воплощенных в строениях, которые, предположим, находятся в свободной продаже. В
таком случае земельные участки, на которых возведены здания, это с точки зрения
настоящего — а именно такова точка зрения отдельного предпринимателя — просто
сырые материалы в особой форме. Допустим также, что z — количество
капитала, привлеченного для нескольких целей. Все формы капитала, включая
авансирование заработной платы, закупку сырых материалов, их использование,
исчисление износа его производственных мощностей любого рода, сами
производственные мощности и землю, на которой они расположены, и т.д. Время
использования тех или иных частей капитала различно, но мы должны свести его на
основе "сложного процента", т. е. геометрической прогрессии, к стандартной
единице, например году.
Допустим, наконец, что и является денежным эквивалентом его собственных
труда, забот, волнений, износа и т.д., связанных с ведением дела. Кроме этих,
есть еще несколько элементов расходов, которые можно было бы выделить в
самостоятельные группы, но которые мы включили в указанные четыре категории.
Таким образом, следует сделать поправку на риск, разделенный между последними
двумя категориями. Соответствующие общие расходы на ведение дела
("дополнительные издержки", см. кн.V гл.IV) будем считать распределенными между
этими четырьмя категориями расходов: на заработную плату, сырые материалы,
процент на капитальные затраты по организации предприятия (его поддержание в
надлежащем состоянии) и вознаграждение собственных работы, предпринимательства и
волнений строителя.
При этих условиях V представляет совокупные затраты строителя, а Н
— его валовую выручку; его усилия направлены на максимизацию Н – V. Тогда
мы получаем уравнения, подобные тем, которые приведены ниже:
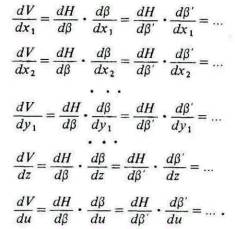
Согласно этим уравнения, предельные затраты, которые строитель склонен
произвести ради незначительного прироста предложения — бх1 — труда
первого вида, а именно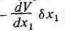 
равны
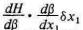т.е. тому
приросту его общей выручки Н, который он получает от расширения жилых
удобств за счет незначительного увеличения предложения труда первого вида; если
речь идет о складских или других удобствах, эта сумма не меняется.
Следовательно, его ресурсы оказываются распределенными между различными видами
использования таким образом, что он ничего не выигрывает от перемещения из
одного вида строительства в другой ни любой части любого фактора
производства—труда, сырых материалов, использования капитала, — ни собственного
труда и предпринимательства; точно так же он ничего не выигрывает ни от замены
любого фактора производства другим в любой отрасли своей деятельности, ни от
расширения или сокращения использования того или иного фактора. С этой точки
зрения наши уравнения по направленности очень схожи с приведенными в гл. V кн.
III аргументами относительно выбора различных способов использования одних и тех
же товаров. Сравните с одним из наиболее интересных примечаний —F— к
великолепному посланию проф. Эджуорта Британской ассоциации в 1889 г.)
К сказанному следует немного добавить (см. кн. V, гл. XI, § 1, и кн. VI, гл.
I, § 8) о трудности интерпретации термина "чистый продукт" какого-либо фактора
производства, идет ли речь о каком-нибудь виде труда или иного фактора, и,
возможно, последние страницы этого примечания — хотя они и непосредственно
вытекают из предыдущего — будут более удобными для чтения. Строитель заплатил
(dV/dx1) * бx1 за последнюю часть труда первого вида, потому что это
его чистый продукт, и, если этот труд был направлен на строительство жилых
домов, он принес выручку ( dH / dв ) * ( dв / dx1 ) * бx1.
Если обозначить теперь цену единицы жилого удобства через р, а его
количество - через в, и тогда рв будет ценой,
вырученной строителем за все количество в; и если мы для краткости заменим (
dв / dx1 ) * бx1, где бx1 — прирост жилого
удобства за счет дополнительного вложения труда, на ^в, то чистый
продукт окажется равным не р * ^в, а (р * ^в) + (в * ^р), где ^р -отрицательная
величина, выражающая падение цены спроса, вызванное приростом жилого удобства.
Для определения относительных значений этих двух элементов — (р * ^в) и (в * ^р)
мы должны провести небольшое исследование.
Если строитель монополизировал предложение жилых домов, в будет
выражать совокупное предложение, и если эластичность спроса окажется меньше
единицы, то увеличение предложения в приведет к сокращению его
общей выручки и (р * ^в) + (в * ^р) станет отрицательной
величиной. Однако он никогда не расширяет производство до таких масштабов, при
которых спрос становится столь неэластичным. Предел, который он ставит перед
производством, будет, наверное, таким, при котором отрицательная величина (в
* ^р) меньше, чем (р * ^в), но не обязательно настолько
меньше, чтобы этой разницей можно было пренебречь. Это главный момент в теории
монополий, рассмотренной в гл. XIV кн.V.
Это ключевой момент и для любого случая, когда деловые связи производителя
ограничены и не могут быть быстро расширены. Если его потребители уже приобрели
столько его товаров, сколько им было нужно, и эластичность их спроса поэтому
временно меньше единицы, дополнительная работа на него еще одного человека может
принести ему убытки, как если бы этот человек работал впустую. Эта опасность
временного перенасыщения конкретного рынка - важнейшее последствие в анализе
многих проблем стоимости по отношению к коротким периодам (см. кн. V., гл. V,
VII, XI), особенно к тем периодам торговой депрессии и тем основам деятельности
торговых ассоциаций, формальным или неформальным, которые мы рассмотрим во
втором томе. Анализ случая, когда каждое увеличение объема производства приводит
к резкому снижению производственных затрат, сопряжен с дополнительными
трудностями, но причины, которые определяют масштабы производства в таких
случаях, настолько сложны, что их едва ли стоит пытаться перевести на язык
математики. См. кн. V, гл XII, § 2.
Следовательно, когда мы изучаем действия отдельного пред принимателя с целью
установить нормальную связь причин, управляющих общим спросом на несколько
факторов производства, мы, вполне понятно, должны избегать подобных случаев. Мы
должны оставлять их специфические черты для специального анализа и
иллюстрировать исследование нормальными случаями, когда индивид — лишь один из
многих предпринимателей, имеющих прямой или косвенный доступ на данный рынок.
Если (в * ^р) численно равно (р * ^в), где в
- совокупное производство на определенный рынок, и отдельный предприниматель
производит часть в' этого продукта — тысячную долю в,
тогда увеличение выручки от добавления еще одного человека равно (р * ^в'),
т. е. (р * ^в), а уменьшить его нужно только на (в' *
^р), которое равно лишь тысячной доле (в * ^р) и может быть
опущено. Поэтому для иллюстрации части общего действия законов распределения мы
вполне можем говорить о стоимости чистого продукта предельной работы любого
фактора производства как о количестве чистого продукта при его нормальной
продажной стоимости, т. е. как о (р * ^в).
Мы видим, что ни одна из этих трудностей не зависит от системы разграничения
видов труда и работ для целей оплаты, хотя заметными эти трудности делает наша
привычка измерять усилия и удовлетворение ценой, с которой они ассоциируются.
Робинзон Крузо, строя для себя дом, не обнаружил бы, что прибавление одной
тысячной части к имевшимся у него удобствам увеличивает его комфорт тоже на
1/1000 . Природа того, что он добавляет, такова же, что у того, к чему он
добавляет, но учитывая добавление по той же норме реальной стоимости для Крузо,
следует учитывать также и то, что новая часть делает старую несколько менее
необходимой, т.е. несколько снижает ее реальную стоимось (см. сноску ккн.V гл.IX)
.С другой стороны, закон убывающей отдачи может сделать очень трудным для него
отнесение его действительного чистого продукта к данной получасовой работе.
Предположим, например, что какие-то мелкие растения, годные в качестве приправы
и занимающие мало места, растут в той части острова, до которой нужно добираться
полдня, и он идет туда, чтобы набрать небольшую партию. Затем он проводит там
целый день, не имея никаких важных дел, которые можно выполнить меньше чем за
полдня, и возвращается с грузом, в десять раз большим. В этом случае мы не можем
выделить отдачу последнего получаса, поэтому мы должны взять в качестве единицы
измерения целый день и сравнить удовлетворение от этого дня с отдачей от других
дней, проведенных иначе. По отношению к современной системе отраслей мы решаем
аналогичную, только более трудную задачу, принимая за единицу для тех же целей
весь процесс производства. Можно было бы расширить приведенные выше системы
уравнений и до таких пределов, когда они полностью охватили бы проблему спроса
как часть проблемы распределения. Однако, хотя математическая иллюстрация
взаимодействия определенной группы причин может быть совершенной сама по себе и
абсолютно точной в рамках своих ограничений, любая попытка отразить рядом
уравнений какую-либо сложную проблему реальной жизни целиком или хотя бы
значительную ее часть обречена на неудачу, поскольку многие важные аспекты,
особенно те, которые связаны с разнообразным влиянием фактора времени, выразить
математически нелегко, поэтому их приходится или опускать полностью, или ужимать
и обрезать таким образом, что они становятся похожими на условных птичек и
животных декоративного искусства. Это порождает тенденцию к неправильному
отражению экономических пропорций, поскольку наибольшее внимание уделяется тем
элементам, которые легче исследовать с помощью аналитических методов. Такая
опасность, без сомнения, существует в любом приложении не только математических
методов, но и анализа любого рода, когда рассматриваются проблемы реальной
жизни. Об этой опасности экономист должен постоянно помнить более, чем о
какой-либо другой. Однако избежать ее полностью — означало бы ограничить
использование главных средств научного прогресса, и в работах, написанных
специально для читателя-математика, без сомнения, правильно смело идти на
широкие обобщения.
Например, в таких работах правильно, может быть, считать H суммой
совокупного удовлетворения и V — суммой совокупного неудовлетворения
(усилия, жертвы и т.д.), которые вызываются в обществе экономическими причинами;
упрощать отражение этих причин с помощью допущений, как поступали более или
менее осознанно и мы, рассматривая различные формы концепции о том, что точкой
устремления этих причин является достижение максимального удовлетворения
и чистое совокупное удовлетворение (см. ранее, кн.V гл.XIII) .другими словами, о
том, что существует постоянная тенденция достичь максимума удовлетворения для
общества в целом. Исходя из этого, общие дифференциальные уравнения того же
вида, что и те, которые мы анализировали выше, можно интерпретировать как
представление о том, что во всех областях экономики стоимость управляется
балансированием групп полезностей с группами бесполезностей, групп
удовлетворений с группами реальных издержек. Подобные построения занимают свое
место в науке, однако не в таком анализе, как здесь, где математика используется
только для выражения более сжатым и точным языком тех средств анализа и
доказательства, которыми более или менее сознательно пользуются в делах
повседневной жизни обыкновенные люди. Действительно можно согласиться, что
подобные построения имеют точки соприкосновения с примененным в кн. III методом
анализа общей полезности конкретных товаров. Различие главным образом в степени,
но эта степень настолько велика, что практически равна разнице между
категориями, поскольку там мы брали каждый товар в отдельности и в отношении к
конкретному рынку и мы тщательно учитывали условия потребителей в данное время и
в данном месте. Таким образом, мы следовали — только, может быть, с более
тщательными предосторожностями — практике обсуждения финансовой политики
министрами финансов и членами палаты общин. Мы указывали, что некоторые товары
потребляются главным образом богатыми, следовательно, их реальные полезности
меньше, чем денежные выражения этих полезностей. Однако мы допускали, как и весь
мир, что реальные полезности двух товаров, потребляемых главным образом
богатыми, относятся друг к другу, как правило (и при отсутствии
противодействующих причин), почти так же, как их денежные выражения, и что это
же верно и для товаров, потребление которых в близкой пропорции разделено между
богатыми, средними и бедными классами. Такие оценки являются лишь грубыми
приближениями, но каждая конкретная трудность — каждый источник возможных ошибок
возникает из неопределенности наших выражений: мы не вводим допущений, которые в
обычной жизни не скрыты, мы не покушаемся ни на какие задачи, кроме тех, которые
в более грубых формах, но с добрыми намерения ми решаются в повседневной .жизни,
мы не вводим новых предпосылок и ярко освещаем то, чего нельзя не заметить.
Однако то, что возможно, когда мы рассматриваем отдельные товары и их связь с
конкретными рынками, не представляется возможным по отношению к несметному числу
экономических элементов из всеохватывающего невода доктрины максимального
удовлетворения. Особенно неоднородны и сложны факторы предложения, которые
включают бесконечное множество прямых и косвенных усилий и жертв, приносимых
представителями всего многообразия индустриальных групп, и, если бы не было
никаких других помех для конкретной интерпретации этой доктрины, непреодолимым
препятствием стало бы ее неявное допущение о том, что воспитание детей и
подготовку их к работе можно измерять тем же способом, что и создание машины.
Примерно по тем же причинам наши математические
примечания будут тем более узки и тем менее основательны, чем сложнее
обсуждаемый в тексте предмет. Часть дальнейших примечаний относится к
монополиям, отдельные стороны которых исключительно доступны для прямой
аналитической интерпретации. Но большинство остальных представляет собой
объяснения сопряженного и совместного спроса и предложения, имеющие много общего
с содержанием данного примечания, а последнее из этой серии — примечание XXI —
задает направление общего обзора проблемы распределения и обмена (без учета
фактора времени), но лишь в таких пределах, которые достаточны, чтобы убедить в
том, что математические объяснения ведут к системе уравнений, число которых не
больше и не меньше, чем число введенных в них неизвестных.
Математическое приложение. -
Замечание XIV bis
На диаграммах, приведенных в этой главе (кн.V гл.VI), все кривые спроса имеют
положительный наклон, и в наших математических интерпретациях этих кривых мы
будем предполагать определенность предельных затрат по продукту такой, какой в
реальной жизни не существует: мы не будем принимать во внимание время,
необходимое для создания солидного предприятия, крупные масштабы которого
приносят и внешнюю и внутреннюю экономию, и будем игнорировать все те трудности,
связанные с законом убывающей отдачи, которые рассмотрены в гл. XII кн. V. Любой
другой путь приведет нас к математическим усложнениям, которые и без попытки их
использования окажутся непригодными для подобного анализа. Поэтому рассуждения,
приведенные в данном и последующих примечаниях, следует считать скорее
набросками, чем законченными исследованиями.
Пусть факторами производства какого-то товара А будут а1, a2 и
т.д., а уравнениями предложения на них у = ф1 (х), у = ф2 (х) и т.д. И
пусть числом единиц этих факторов, необходимым для производства х единиц товара
А будет выражено рядом m1х, m2x,..., где m1, m2 - не
константы, а функции х. Тогда уравнением спроса на А будет
Пусть также у = F(x) будет уравнением спроса для готового товара.
Тогда уравнение спроса для аr, примет вид
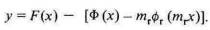
Однако в этом уравнении у — цена не единицы фактора, а m
единиц, поэтому, чтобы получить уравнение, выраженное в терминах фиксированных
единиц, обозначим цену единицы через П, и если E= mrх и тогда П
= 1/mr , уравнение принимает вид
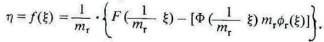
Если m1 - функция х, равная,
скажем, Ш (х), тогда х следует выразить с помощью E
уравнением E =xШr(x); тогда m1 можно записать как xr(E).
Подставляя это выражение в формулу, мы получаем П, выраженное как функция
Е. Тогда уравнением спроса для аr будет просто П = Фr (E).
Математическое приложение. -
Замечание XV
Пусть уравнением спроса для ножей будет
y = F(x) - (1) ,
уравнением предложения ножей
y = Ф (x) - (2),
предложения ручек
у = ф1(х) - (3),
предложения лезвий
у = ф2 (х) - (4),
тогда уравнением спроса для ручек будет
y = f1 (x) = F (x) - Ф2 (x) -
(5),
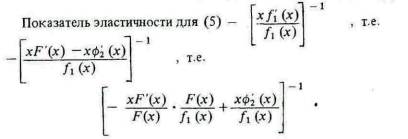
Он будет тем меньше, чем полнее выполняются условия: (I) что - (x *
F' (x)) / F (x), которое обязательно положительно, велико, т.е. что
эластичность спроса на ножи невелика; (II) что ф'2 (х)
положительно и велико, т. е. что цена предложения для лезвий резко растет, или
падает при возрастании или снижении предложения; и что (III) F (x) / f'(x)
велико, т. е. что цена ручек составляет лишь незначительную часть цены ножей.
Если принимать единицы факторов производства не
постоянными, а переменными, как в предыдущем примечании, аналогичное, но более
сложное построение приведет, в сущности, к тем же результатам.
Математическое приложение. -
Замечание XVI
Предположим, что m бушелей хмеля используется в производстве одного
галлона эля определенного сорта, х' равновесного количества которого
продано по цене у'= F(x'). И пусть m изменится на m + ^m и в
результате х' галлонов, по-прежнему предложенных для продажи, найдут
покупателя при цене у' + ^y'. Тогда ^y' / ^m будет представлять
предельную цену спроса для хмеля; если она больше, чем цена предложения, для
пивоваров будет выгодно класть больше хмеля в эль. Возьмем более общий случай,
где у = F(x, m), у=Ф(х, m) — уравнения спроса и предложения для пива,
х — число галлонов и m — число бушелей хмеля, идущего на один галлон.
Тогда F(x, m) — Ф(х, m) — превышение спроса над ценой предложения. В
состоянии равновесия оно, разумеется, равно нулю, но если бы можно было,
варьируя т, добиться положительной разности, положение изменилось бы. Поэтому
(предполагая, что в затратах на производство пива не происходит других заметных
изменений, кроме тех, что вызываются увеличением количества хмеля) dF/dm = dФ/dm
, где первое отношение представляет предельную цену спроса и второе - предельную
цену предложения хмеля, которые по указанной причине равны друг другу.
Этот метод, конечно, можно распространить и на
случаи, в которых одновременно варьируют два или более факторов производства.
Математическое приложение. -
Замечание XVII
Предположим, что какой-то товар, будь то материальная вещь или фактор
производства, распределен между видами использования так, что в первый из них
идет х1 из общего количества х, а во второй — х2. Пусть
у = ф(х) — уравнение общего предложения, a y=f1(x1) и y=f2(x2)
- уравнения спроса для первого и второго видов использования. Тогда равновесие
трех неизвестных х, x1, х2 определяется тремя уравнениями f1 (х1)= f2
(x2)=ф(x); x1+x2=x.
Предположим далее, что нам желательно
установить соотношение спроса и предложения для первого вида использования при
условии, что при любом их изменении равновесие между спросом и предложением во
втором виде использования сохраняется, т. е. что при любом фактическом объеме
производства этого товара цена спроса для второго вида использования равна цене
предложения: f2(x2) всегда равно Ш(х1 +х2). Из этого уравнения мы
можем определить х2 через х1 и поэтому х через х1,
следовательно, можем записать Ш(х) =Ш(хl). Таким образом, уравнение
предложения для первого вида использования данного товара принимает вид y=Ш(х1),
и это выражение вместе с уже известным уравнением y=f1(x1) дает искомое
соотношение.
Математическое приложение. -
Замечание XVIII
Пусть а1, а2... - сопряженные продукты, а m1х, m1х,... их
раздельно произведены х единицами общего процесса производства, уравнение
предложения для которого имеет вид у = ф (х) . Пусть
y = f1(x), y=f2(x),...
соответствующие уравнения спроса на них. Тогда для условий равновесия
m1 * f1(m1 * x) + m2 * f2(m2 *
x) + ... )= ф(x).
Пусть х' - значение х, полученное
из этого уравнения; тогда f1(m1 * x'), f2(m2 * x') - цены равновесия для
нескольких сопряженных продуктов. Разумеется, m1, m2, если это
необходимо, выражены через х'.
Математическое приложение. -
Замечание XIX
Этот случай mutatis mutandis
корреспондирует со случаем, рассмотренным в примечании XVI. Если в состоянии
равновесия х' быков поставляются за год на рынок и продаются по цене
у'=ф(х'), а каждый бык дает m единиц мяса; и, если скотоводы приходят
к выводу, что, изменив технологию откорма быков, они могут увеличить их привес
на ^m единиц мяса (отход шкур и других сопряженных продуктов остается
неизменным) и что дополнительные расходы на это составят ^y', тогда
предельная цена предложения мяса будет представлена выражением ^y' / ^m .
Если эта цена меньше цены продажи, данное изменение выгодно для скотоводов.
Математическое приложение. -
Замечание XX
Пусть а1, а2 ... - товары, пригодные для
осуществления одной и той же функции. Пусть единицы их измерения подобраны так,
что единица одного из них эквивалентна единице любого другого. И пусть
уравнениями их предложения будут у1 = ф1 (х1) ,у2 = ф2 (х2) ,... Пусть
переменные этих уравнений изменились, и мы можем записать их в виде x1 =
Ш1(y1) , х2 = Ш2(у2),... . Пусть у = f(x) будет уравнением спроса на
услугу, для предоставления которой подходит каждый из этих товаров. Тогда для
состояния равновесия х и у определяются уравнениями у =f(x); х
= х1 + х2 + ..., у1 = у2= ...=y. (Эти уравнения должны быть такими, чтобы ни
одно из чисел х1, х2... не было отрицательным. Когда у1 снижается
до определенного уровня, x1 становится равным нулю и остается равным нулю
для более низких значений x1.) Как показано в тексте, мы должны считать в
этом случае, что данные уравнения предложения полностью удовлетворяют
требованиям закона убывающей отдачи, т.е. что ф1'(х), ф2 '(x),... всегда
имеют положительные значения.
Математическое приложение. -
Замечание XXI
Теперь мы можем полностью охватить взглядом проблему совмещенного спроса,
совокупного спроса, совмещенного предложения и совокупного предложения, когда
они увеличиваются одновременно; с целью убедиться в том, что наша абстрактная
теория включает ровно столько уравнений, сколько в ней неизвестных — не больше и
не меньше.
Для проблемы совмещенного спроса мы можем предположить, что есть n
товаров A1, A2,... Аn. Пусть в производстве товара A1 используется
a1факторов производства, товара A2 —a2 факторов и т.д., так что
общее число факторов m = a1 + a2 + a3 + ...+an. Предположим вначале, что
все факторы автономны, т.е. что совокупного спроса не существует, что у каждого
фактора свой процесс производства и поэтому нет сопряженных продуктов и,
наконец, что никакие два фактора не имеют общего использования, т.е. что не
существует совокупного предложения. Тогда мы получаем 2n + 2m
неизвестных, выражающих количества и цены п товаров и т факторов, и имеем для их
определения 2m + 2n уравнений, а именно: (I) n уравнений спроса,
каждое из которых связывает цену и количество отдельного товара, (II) n
уравнений, каждое из которых приравнивает цену предложения для любого количества
отдельного товара к сумме цен соответствующих количеств факторов, используемых в
его производстве; и, наконец, (III) m уравнений предложения, каждое из
которых устанавливает количество отдельного фактора, использованного в
производстве данного количества данного товара.
Учтем теперь не только совмещенный, но и совокупный спрос. Пусть в1
факторов производства имеют одинаковое содержание, например выражают труд
плотника определенной производительности; другими словами, пусть одним из
факторов производства количества в числа n товаров A1,
А2, ... является труд плотника. Тогда, поскольку принимается, что в любом
производстве, где он используется, труд плотника имеет одну цену, для каждого
фактора производства существует только одна цена, и число неизвестных можно
сократить на в1-1, точно так же мы можем сократить и число
уравнений предложения на в1- 1 и поступить подобным же образом во
всех остальных случаях.
Теперь введем в расчет и совмещенный спрос. Пусть У - количество
товаров, используемых в производстве изделий, которые являются сопряженными
продуктами одного и того же процесса. Тогда количество неизвестных не изменится,
а число уравнений предложения уменьшится на (У1 — 1), но это сокращение
компенсируется новым рядом (У1 — 1) уравнений, связывающих количества
этих сопряженных продуктов, и т. д.
Пусть, наконец, один из используемых товаров
имеет совокупное предложение, обеспечиваемое за счет б1 конкурирующих
источников. Тогда, сохраняя старые уравнения предложения для первого из этих
источников, мы имеем 2(б1 — 1) дополнительных неизвестных, выражающих
цены и количества остальных 2(б1 — 1) источников. Чтобы отразить эти
неизвестные, нужны 2(б1 — 1) уравнений предложения для конкурирущих
источников и 2(б1 — 1) уравнений, отражающих цены б1 источников.
Таким образом, сколь сложной ни становится проблема, она остается теоретически
разрешимой, потому что число неизвестных всегда строго равно числу получаемых
нами уравнений.
Математическое приложение. -
Замечание XXII
Если y=f1 (х), у =f2 (х) -уравнения соответственно кривых спроса и
предложения, то объем производства, обеспечивающий максимальный монопольный
доход, находится максимизацией [xf (х) —xf (х)], т.е. корня или одного из
корней уравнения
функция предложения представлена здесь f1
(х) вместо ф(х), как ранее, чтобы подчеркнуть тот факт, что цены
предложения выражают здесь не совсем то же самое, что и в предыдущих замечаниях.
Мы отходим здесь к такой системе нумерации кривых, которая исключает ошибочное
впечатление, что их число увеличилось.
Математическое приложение. -
Замечание XXIII
Если вводится налог, совокупная величина которого выражается F(x),
тогда, чтобы найти значение х, максимизирующее монопольный доход, мы имеем
уравнение
и ясно, что,если F(x) -константа, как при взимании лицензионной
пошлины, или варьирует в виде разности x * f1 (х) - x * f2 (х), как при
взимании подоходного налога, данное уравнение имеет те же корни, как и при F(x)
= 0. При геометрическом анализе проблемы мы видим, что если установлен
фиксированный налог на монополию, достаточный, чтобы кривая монопольного дохода
вся оказалась ниже Ox, a точка q лежала на новой кривой ниже L
на втором графике в гл.XIV кн.V , тогда точка q', в которой новая кривая
касается одной из ряда гипербол, находится как пересечение линии уО,
опущенной с одной асимптоты, и Ox — с другой. Эти кривые можно назвать
кривыми постоянных потерь.
При ставке налога на монопольный доход, равной
m (m < 1), QQ' будет заменена кривой, каждая ордината которой находится
как (1 — m) умножить на ординату соответствующей точки на QQ' т.
е. точки, лежащей на той же абсциссе. Проецирование наглядно показывает нам, что
касательные к корреспондирующим точкам QQ' в старом и новом ее положениях
будут пересекать Ох в одной точке. Однако о гиперболах, расположенных в
прямоугольной системе координат и имеющих одни асимптоты, мы знаем, что если
провести линию пересечения гипербол, параллельную одной из асимптот, и
касательные к ним в точках пересечения, то все эти касательные пересекут другую
асимптоту в одной точке. Поэтому если g3' — точка на новой QQ',
соответствующая точке g3, и если мы обозначим G точку, в которой
общая касательная к гиперболе и к QQ' пересечет Ох, то Gg3'
будет касательной к гиперболе, проходящей через g3'; т. е. g3' -
точка максимального дохода на новой кривой. Геометрические и аналитические
методы, изложенные в данном примечании, применимы к случаям, подобным тем,
которые рассмотрены в последней части § 4 текста: налогообложения монопольного
продукта.
Математическое приложение. -
Замечание XXIV
Пусть ^x - вероятный объем его производства в период ^t, а ^у -
вероятный объем его потребления. Тогда дисконтированная стоимость его будущих
услуг определяется как
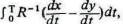
где Т — максимально возможная продолжительность его жизни. Точно так
же прошлые издержки его воспитания и обучения выражаются интегралом
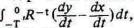где T'—момент
его рождения. Если мы предположим, что он ничего не добавляет к материальному
богатству той страны, в которой он остается всю свою жизнь, и ничего не берет из
него, мы получим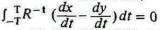 
или, принимая
за нижний предел момент его рождения и l = Т' + Т — за максимально
возможную продолжительность его жизни, в более простой форме
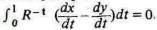. Говорить,
что ^x — это вероятный объем его производства за период ^t,—это
значит кратко отмечать то, что более точно можно выразить следующим образом:
пусть р1, р2,... — вероятности, что за период ^t он произведет
элементы богатства ^1x, ^2х,..., где p1 +р2 + ...= 1, и один или
более рядов ^1х, ^х,... могут быть нулевыми; тогда
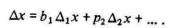
Содержание