§ 8. Мультипликатор. Равновесный объем производства в кейнсианской модели

Модель мультипликатора

Анализ инвестиционных процессов показывает, что увеличение чистых инвестиций генерирует мультипликативный рост ВНП. Иначе говоря, инвестируемые деньги - это деньги «повышенной мощности». К аналогичному эффекту приводит и изменение государственных расходов. Это усиленное влияние инвестиций и государственных расходов на рост ВНП получило название «мультипликативного эффекта», а модель, описывающая данные взаимодействия, - «модели мультипликатора».

Очевидно, что независимо от источника расходов (будь то частные инвестиции I или государственные расходы G), чем выше у экономических агентов дополнительный потребительский расход (т.е. склонность потреблять), тем сильнее отмеченный мультипликативный эффект. Напротив, чем выше склонность к сбережению (а значит, и дополнительная «денежная утечка» при каждом денежном обороте доходов), тем указанный эффект слабее.

В наиболее общем виде модель мультипликатора может быть записана в виде:

?Y = k ?F,

где ?Y - прирост национального продукта (дохода), индуцированный увеличением расходов на величину ?F; k - числовой коэффициент, называемый «мультипликатором». Конструкция коэффициента k достаточно проста. Любой дополнительный расход ?F, поступающий в экономическую систему, одновременно означает доход экономических агентов, получаемый ими в оплату за товары и оказываемые услуги. Проходя многочисленные цепочки трансформаций, этот доход каждый раз уменьшается на сберегаемую тем или иным экономическим агентом часть. В свою очередь, потребляемая часть передается в оплату потребляемых товаров и услуг другому экономическому агенту и т.д.

Если предположить наличие фиксированной величины предельной склонности потребления МРС для всех хозяйственных агентов, независимо от размеров получаемых ими доходов, и положить МРС = q, то тогда общий доход (национальный продукт как сумму доходов), генерируемый расходами dF, можно выразить следующим образом:

?Y= (1 + q + q2 + q3+ ...)?F.

Поскольку q < 1, мы имеем бесконечную убывающую прогрессию 1 + q + q + q2 + q3 + ... Хорошо известно, что ее сумма равна 1 / 1 - q. Отсюда:

k + L/ L- q = L/ L- МРС.

Вместе с тем, чтобы собрать дополнительные средства для государственных расходов при существующей зависимости между размерами личного потребления и величиной ВНП, потребуется собрать дополнительные налоги. Однако увеличение налогов при прочих равных условиях будет способствовать сокращению потребления С.

На рисунке 13.4 показано, что увеличение государственных расходов с G до G1 вызовет сдвиг вверх кривой С + I + G на величину G1 - G. Исходная точка общего экономического равновесия Е переместится в положение Е1, что будет соответствовать увеличению национального продукта с Q до Q1 и увеличению инвестиций с I до I1 (последнее потребует часть государственных расходов при фиксированном уровне частных инвестиций (I) направить на капитальные вложения). Вместе с тем, поскольку наклон прямой С + I + С2 полностью определяется характером потребления, то для того, чтобы переместить ее в положение, соответствующее состоянию общего экономического равновесия Е, потребуется налог в размере LK. Именно эта величина налога будет соответствовать сокращению потребления на величину Е1К. Заметим также, что отношение E1K / LK - это не что иное, как предельная склонность к потреблению МРС, имеющая место в обществе. Определив мультипликатор налога как n = Q1 - Q / LK, нетрудно увидеть, что

n = Q1 - Q / LK = Q1 - Q / Е1К * Е1К / LK.

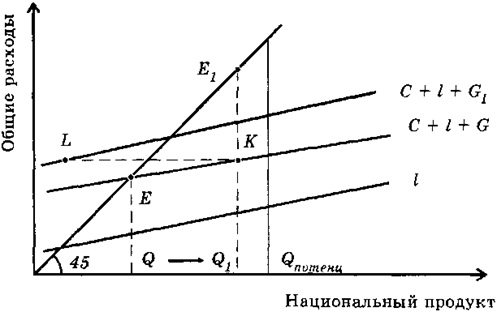
Рис. 13.4. Определение состояния равновесия в зависимости от С, I, G

Но Е1 К / LK = МРС, a Ql - Q / E1K - это не что иное, как мультипликатор расходов. Таким образом, мультипликатор расходов и мультипликатор налога связаны следующим образом:

n = К * МРС = МРС /1 - МРС.

Мультипликатор налога при изменении состояния общего экономического равновесия содержит в себе очень полезную для аналитиков информацию. Он показывает относительную величину изменения ВНП, генерируемую каждый рублем увеличения (уменьшения) налогового бремени.

Подчеркнем также, что точки общего экономического равновесия Е и Ег соответствуют состояниям равенства совокупного спроса и предложения, которые рассматривались ранее (см. рис. 13.2).

< Назад   Вперед >
Содержание