§ 3. Производственная функция и спрос на ресурсы
Предельная доходность ресурсов и фирма
Деятельность фирм в условиях рыночного ценообразования на факторы производства строится на экономических расчетах предельной эффективности затрат и выпуска продукции.
Критерием здесь выступает предельная доходность ресурсов. Она измеряется показателями изменения доходов фирмы от продажи выпускаемой продукции, произведенной с помощью использования дополнительной единицы каждого ресурса.
Рыночное ценообразование на факторы производства, особенности их предложения и спроса формируют условия, укладывающиеся в классическую «модель» поведения фирм. В экономической теории производства они получили название закона «затраты-выпуск» и представляют собой систему инженерных расчетов производственной функции фирмы.
Каждая фирма осуществляет экономические расчеты объема выпуска продукции и количества необходимых для этого ресурсных затрат. В наиболее общем виде - это расчет фирмой собственной производственной функции. Производственную функцию любой фирмы можно представить в следующем виде:
Q = ?(L, К),
где Q - объем выпуска продукции; L - количество используемого труда; К - объем капитала (технических средств) фирмы.
Таблица 8.1 Числовой пример производственной функции фирмы
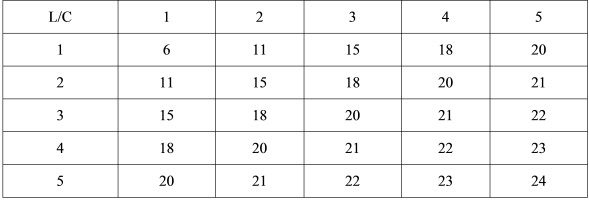
В табл. 8.1 представлен гипотетический производственный процесс, технология которого предполагает сочетание только двух факторов - капитала и труда.
По вертикали указано количество единиц капитала, по горизонтали - численность работников. Размеры выпуска продукции показаны на пересечении каждой единицы капитала и
труда-
Данный пример производственной функции показывает возможные сочетания количественно изменяющихся затрат факторов производства и максимально возможный результат такого сочетания - выпуск продукции.
Современная национальная экономика - это десятки миллионов производственных функций. Для каждой фирмы вычисление своей производственной функции означает нахождение оптимального соотношения факторов производства для определенного объема выпуска продукции. Для этого необходима информация о производительности привлекаемых в производство факторов, ценах и издержках на их приобретение, а также ценах и спросе на продукцию, выпускаемую с помощью этих факторов (пример в табл. 8.2).
Таблица 8.2 Производственная функция и динамика результатов экономической деятельности фирмы
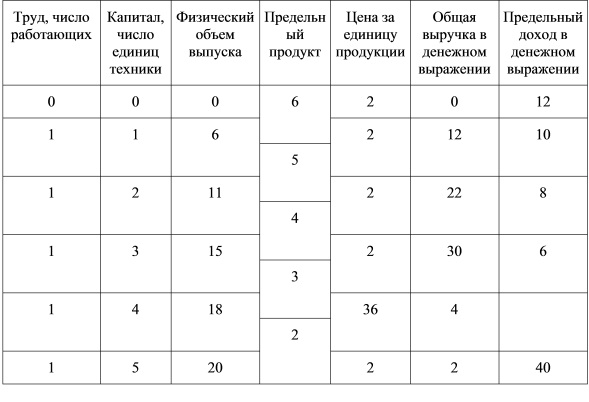
Как видно из табл. 8.2 (колонки 1 и 2), изменение производственной функции отражает изменяющуюся техническую оснащенность труда, поскольку численность работников не изменилась. Вследствие этого возрастает объем выпуска (колонка 3). При стабильности спроса и рыночной цены за единицу продукции (колонка 5) возрастает выручка от продаж продукции (колонка 6).
Однако нетрудно заметить снижающуюся динамику показателей предельного продукта (колонка 4) и получаемого от его продажи предельного дохода (колонка 7). Эти снижения не являются «казусом» условного числового примера, представленного в табл. 8.2. Подобная тенденция означает действие закона снижающейся доходности.
Такая тенденция обнаружится и в том случае, если осуществлять дополнительные приращения труда, оставляя неизменным капитал. Относительное снижение выпуска, улавливаемое показателями предельного продукта, происходит потому, что на каждую добавочную единицу приращиваемого фактора производства приходится все меньшее количество оставшихся неизменными других факторов.
Снижение предельного продукта приостановится, если осуществлять дополнительные приращения не одного, а всех "предусмотренных технологией факторов производства. В результате возрастает не только абсолютный объем выпуска, но и его относительный прирост, т.е. предельный продукт. Единственным ограничителем здесь может служить рыночная цена на выпускаемую продукцию. Если она удовлетворительна для фирмы, то противодействовать тенденции снижающейся доходности можно только за счет расширения масштаба производства, объема выпуска продукции. Достигается это вследствие пропорционального приращения всех факторов производства. На рынках факторов производства возрастет спрос, а следовательно, и цена необходимых для производства факторов и ресурсов
< Назад
Вперед >
Содержание