Структура плоских рычажных механизмов по Ассуру

Рычажными называются механизмы, звенья которых образуют только низшие кинематические пары.

Основной принцип образования плоских рычажных механизмов был впервые предложен русским ученым Л.В. Ассуром в 1914 году. Согласно Л.В. Ассуру любой механизм может быть представлен как полученный присоединением к стойке и начальному звену (при W = 1) или к начальным звеньям (при W > 1) кинематических цепей, называемых группами Ассура.

Начальным звеном называется звено, которому приписывается обобщенная координата.

Группой Ассура называется кинематическая цепь, присоединение которой к механизму не изменяет его числа степеней свободы (т.е. для нее W ?? = 0 – это цепь с нулевой подвижностью).

Установим соотношение между числом кинематических пар цепи и числом ее подвижных звеньев, при котором цепь имеет нулевую подвижность.

Для рычажного механизма формула Чебышева, определяющая число степеней свободы механизма (который представляет собой кинематическую цепь) имеет вид:

W = 3n - 2p1

Применяя эту формулу к рассматриваемым кинематическим цепям (группам Ассура), будем иметь:

W ? = 3n? - 2p?1 = 0, где

n? - число звеньев в группе Ассура,

p?1 - число низших кинематических пар в группе Ассура.

Тогда искомое соотношение между числом кинематических пар в группе Ассура и числом ее подвижных звеньев определится как

p?1 = 3n? /2

Возможное сочетание звеньев и кинематических пар в группах Ассура представим таблицей:

p?1

2ПГ

3ПГ

более сложная

Так как число кинематических пар должно быть целым числом, то число звеньев должно быть четным. Первое четное число 2, при этом число кинематических пар равно 3 - это двухповодковые группы Ассура (2ПГ). Следующее сочетание цифр: число звеньев в группе равно 4, а число кинематических пар - 6. Это трехповодковые группы Ассура (3ПГ). Далее идут более сложные группы Ассура.

Поводком называется звено группы Ассура, образующее низшие кинематические пары с другими звеньями, не входящими в данную группу Ассура.

В зависимости от числа поводков различают двух, трехповодковые и более сложные группы Ассура. Наиболее распространенными являются двухповодковые группы, которые существуют в пяти видах:

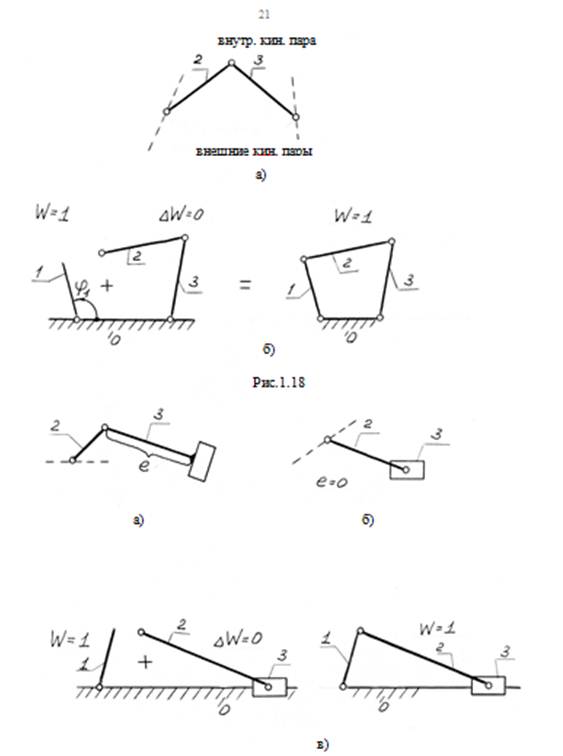
1 вид: ВВВ - содержит три вращательные кинематические пары (рис. 1.18,а).

Образование механизма с помощью этой группы представлено на рис. 1.18,б.

Каждая последующая группа Ассура может быть получена последовательной заменой в двухповодковой группе первого вида вращательных пар на поступательные.

2 вид: ВВП - вращательная, вращательная и поступательная кинематическая пара (рис. 1.19,а,б). Образование механизма с подобной группой Ассура представлено на рис.1.19,в.

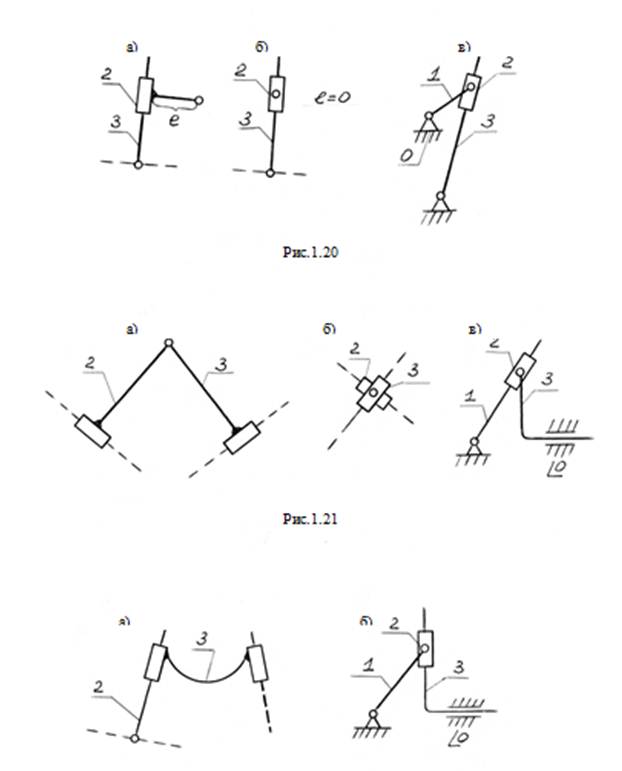
3 вид: ВПВ - вращательная, поступательная и вращательная пара (рис. 1.20,а,б,в).

4 вид: ПВП - поступательная, вращательная и поступательная пара (рис. 1.21,а,б,в).

5 вид: ВПП - вращательная, поступательная и поступательная пара (рис.1.22,а,б).

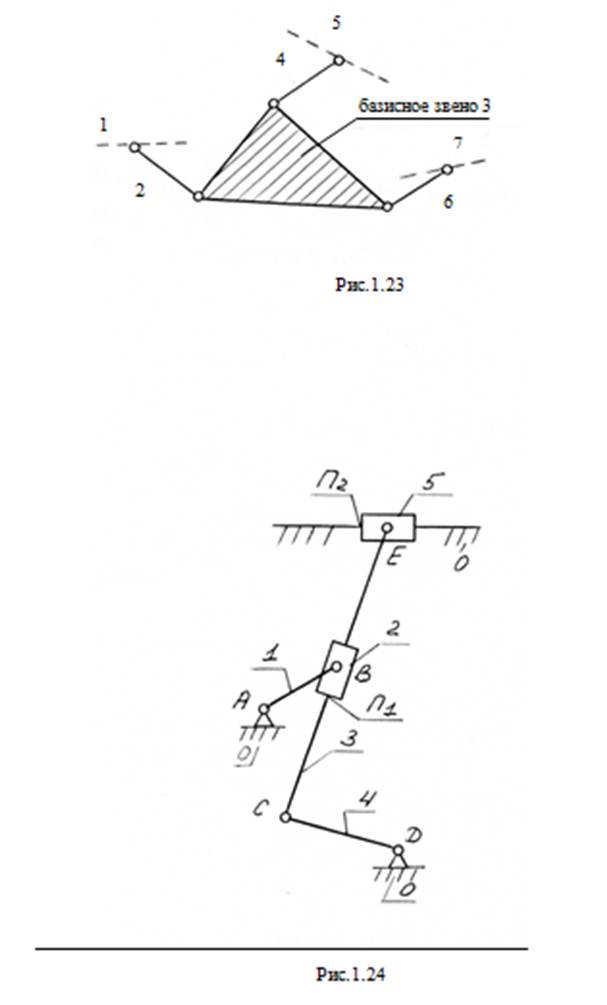
На рис. 1.23 предоставлен один из видов трехповодковой группы Ассура, где звенья 2,4,6 - поводки, а звено 3 - базисное.

1.4.4 Примеры структурного анализа механизмов

Задача структурного анализа заключается в определении числа подвижных звеньев, числа и вида кинематических пар, числа степеней свободы механизма, в разбивке механизма на группы Ассура с установкой последовательности их присоединения к начальному звену и стойке.

Пример. Провести структурный анализ механизма (рис. 1.24).

Согласно формуле (1.1) определим число степеней свободы данного механизма:

n = 5 (кривошип 1, шатун 2, шатун 3, коромысло 4, ползун 5),

p1 = 7 [А(0-1), В(2-3), С(3-4), Д(4-0), Е(3-5), П1(2-3), П2(5-0)],

p2 = 0.

W = 3n - 2p1 - p2 = 3 ? 5 - 2 ? 7 - 0 = 1.

Вариант № 1: начальный механизм образован начальным звеном 1 и стойкой 0:1-0.

Возможные поводки по отношению к начальному звену и стойке: 2, 4, 5. Эти звенья не соединены друг с другом кинематическими парами, поэтому двухповодковых групп здесь нет. Но есть звено 3, которое соединяет все эти звенья между собой. Поэтому имеем трехповодковую группу Ассура (3ПГ), где 3 - базисное звено.

Вариант № 2: начальный механизм образован начальным звеном 4 и стойкой 0: 4-0.

Возможные поводки по отношению к начальному звену и стойке:1, 3, 5.

Звенья 3 и 5 образуют 2ПГ (2вида), так как связаны между собой вращательной парой (шарнир Е).

Поводками по отношению к промежуточному механизму, состоящему из звеньев 0-4-3-5, становятся звенья 1 и 2, которые образуют 2ПГ (2 вида) с внутренней вращательной парой (шарнир В).

Вернуться в оглавление: Теория механизмов и машин