Основные уравнения для определения скоростей и ускорений звеньев

Звено может совершать поступательное, вращательное или сложное движение.

Звено совершает поступательное движение.

Скорости всех точек звена одинаковы по величине и по направлению Аналогично равны по величине и по направлению и ускорения всех точек (рис. 2.1).

Звено совершает вращательное движение.

Известна угловая скорость звена w, угловое ускорение e, длина звена iАВ. Требуется определить скорость VВ точки В и ускорение этой точки аВ (рис. 2.2).

Связь между линейной и угловой скоростью имеет вид: Vв = w ? iАВ [м/с].

Траектория движения точки В - дуга окружности радиуса iАВ; вектор скорости точки В перпендикулярен радиусу и направлен в сторону вращения звена. Полное абсолютное ускорение точки В складывается из двух составляющих: нормальной nв и тангенциальной tв: в = nв + tв или ав =, где

nв = w2 iАВ = V2В/iАВ [м/с2],

tв = e ? iАВ [м/с2]

Нормальное ускорение направлено по звену к его центру вращения; тангенциальное ускорение направлено в сторону углового ускорения e перпендикулярно звену .

Сложное движение звена.

Его можно представить как сумму переносного и относительного движений:

абс = пер + отн

абс = пер + к + r, где к = 2wпер ? Vотн sin(vпер; отн),

wпер - переносная угловая скорость;

Vотн - относительная линейная скорость;

r - релятивное (относительное) ускорение.

Для плоского механизма (vпер;отн) = 900 , следовательно а к = 2wпер ? Vотн.

Существует два способа разложения сложного движения, применяемые в ТММ.

I способ.

Применяется для точек одного звена, когда известны скорость и ускорение одной точки звена (т.В) и требуется определить скорость или ускорение другой точки (т.С) этого же звена ( рис. 2.3).

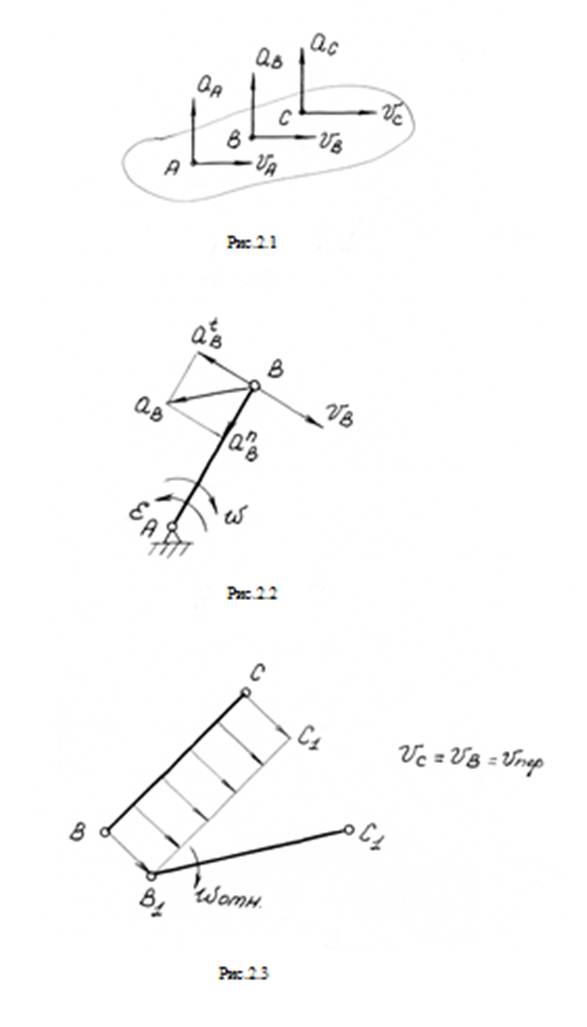
При этом сложное движение точки В раскладывается на переносное поступательное вместе со скоростью (ускорением) точки точки С и относительное вращательное вокруг этой точки.
Пусть для звена ВС известны скорость и ускорение точки В: и . Требуется определить скорость и ускорение точки С.
Если звено ВС в конце движения должно занять положение В1 С1, то можно представить, что вначале все точки звена переместятся параллельно самим себе с одинаковой скоростью С = В = пер в переносном движении, а затем это звено повернется относительно точки В со скоростью wотн:
С = В + СВ
Для скорости VВ известны ее модуль и направление ( в дальнейшем подчеркивание двумя чертами будет означать, что известны как модуль, так и направление рассматриваемого параметра ( в данном случае - скорости), подчеркивание одной чертой означает, что известны или модуль, или направление).
Для относительной скорости VСВ = wотн ? lСВ известна линия, вдоль которой направлена эта скорость (перпендикулярно ВС).
Выражение для определения ускорения точки С будет иметь вид:

ак = 0, так как переносное движение поступательное и wпер = 0.
Относительное движение, вращательное, раскладывается на две составляющие - нормальное и тангенциальное:
, где
аnСВ= V2CB/lСВ = w2отн?lСВ - нормальное ускорение, направленное к центру относительного вращения (точка В),
аtСВ= e?lСВ - тангенциальное ускорение, направленное перпендикулярно звену.

2 способ

Применяется для двух звеньев, образующих поступательную пару (рис.2.4), например, если известно движение звена 2 (направляющей), а требуется определить движение звена 3.

Пусть точка А принадлежит звену 2 (проекцию этой точки на звено 3 обозначим А3). Известно движение точки А звена 2 (скорость А2 и ускорение А2.). Требуется определить скорость и ускорение точки А3 третьего звена: А3 , А3.

Движение звена 3 можно разложить на переносное вместе со звеном 2 и на относительное поступательное звена 3 относительно звена 2 вдоль его направляющей. Переносное движение второго звена может быть поступательным, вращательным, сложным..

Скорость точки А3 третьего звена представим как сумму переносной и относительной скорости:

А3 = А2 + А3 А2

Переносная скорость А2 известна по величине и по направлению,

Скорость А3 А2 точки А3 звена 3 относительно звена 2 направлена параллельно направляющей a - a поступательной пары.

Ускорение точки А3 третьего звена определится уравнением:

А3 = А2 + кА3А2 + r А3А2,,

в котором А2 и акА3А2 известны по величине и по направлению, а именно: А2 -

задано, кА3А2 = 2 • wпер •Vотн = 2w2 • VА3А2.

Для определения направления кориолисова ускорения необходимо вектор относительной скорости повернуть на 900 в направлении угловой скорости wпер = w2 переносного движения.

Определение относительного (релятивного) ускорения аrА3А2:

1. Если направляющие поступательной пары криволинейны (рис. 2.5), то относительное ускорение будет складываться из двух составляющих:

rА3А2 = пА3А2 +tА3А2, где пА3А2 = V2А3А2 / r.

2. Если направляющие прямолинейны (т.е. r = ?), то nА3А2 = 0, аtА3А2 = аrА3А2 и ускорение направлено вдоль направляющей a-a..

Кинематическое исследование механизмов методом построения планов скоростей и ускорений ведётся по группам Ассура в порядке их присоединения к начальному звену и стойке. Для любой группы Ассура известны или могут быть определены скорости (ускорения) внешних кинематических пар и совместным решением двух векторных уравнений можно определить скорость (ускорение) внутренней кинематической пары. При составлении векторных уравнений используются указанные выше два способа разложения движения.

Вернуться в оглавление: Теория механизмов и машин