Аналитический метод кинематического исследования механизмов

Удобно определять не сами скорости и ускорения, а их аналоги. При заданной схеме механизма аналоги скоростей и ускорений являются функциями обобщенных координат механизма или (при W=1) -  обобщенной координаты. Такой путь решения позволяет задачу о кинематическом исследовании свести к задаче об определении некоторых геометрических характеристик схемы, используя которые, при заданном законе изменения по времени обобщенных координат  механизма, можно определить действительную скорость и ускорение.

Предположим, что для механизма с одной степенью свободы определены угол поворота i-ого звена и координаты точки М, как функции обобщенной координаты механизма.

, ,. Здесьq – обобщенная координата, хм - абсцисса точки М,  ум -  ордината точки М.

Определение скоростей

Угловая скорость i-ого звена

  -     по аналогии.

В этих формулах   - первая  производная обобщенной координаты механизма по времени, называемая обобщенной скоростью механизма;

  - производные координат точки М по обобщенной координате механизма – проекции аналога скорости точки М на координатные оси.

Полный аналог скорости точки М:

Скорость точки М:                                  

Определение ускорений

Угловое ускорение для  i-го звена

После преобразований получаем:

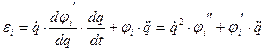
Проекции ускорения точки М на оси  х и у:

,

где  - вторая производная обобщенной координаты по времени.

,   - вторые производные координат точки М по обобщенной координате (проекции аналога ускорения точки  М на координатные оси).

Полный аналог ускорения:

Полное ускорение:

При угловой обобщенной координате обобщенная скорость механизма – это угловая скорость начального звена (размерность с-1), а  -  угловое ускорение начального звена (с-2).

Аналоги угловой скорости и углового ускорения звена являются безразмерными величинами, а аналоги скоростей и ускорений точки имеют размерность длины.

Для этого случая:

           

            

                     

В частном случае, когда  и :

                 ;

Пример аналитического исследования кинематики кривошипно-ползунного механизма

Применим метод замкнутых векторных контуров (метод Зиновьева).

Условие замкнутости контура, составленного звеньями механизма, записывается в векторной форме. Затем слагаемые этого равенства проецируются на координатные оси, что позволяет получить уравнения, определяющие положение звеньев и их точек. Последовательным дифференцированием этих уравнений определяют аналоги скоростей и ускорений.

Условие замкнутости контура ABCA  (рис. 2.16) запишется в виде:

Проекции векторов этого равенства на оси Xи Y дают:

                          (а)

                           (б)

Углы   и  отсчитываются от положительного направления оси абсцисс.

Из второго уравнения найдем  функцию положения звена 2:

,              (в)

где  ;

 

      

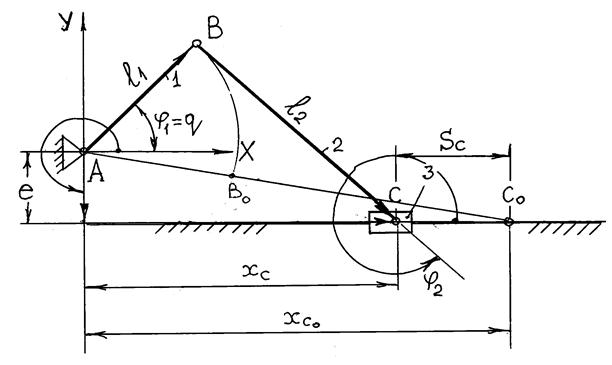
                                                                       Рис. 2.16

 Положение ползуна удобно задавать от его правого крайнего положения: , где  - координата, определяющая крайнее правое положение ползуна. С учетом выражения (а)                       .

Определим далее аналоги скоростей:

 - для шатуна 2, и   - для ползуна 3.

Дифференцируя выражение (в) получим:    , откуда

Аналог  скорости ползуна найдется, как

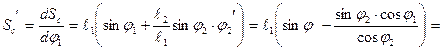
Аналоги ускорений:

.                               

    

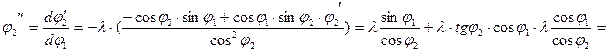
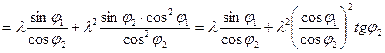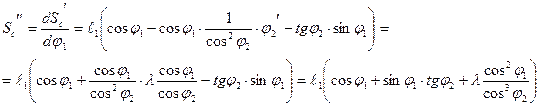
Таким образом, имея выражения, определяющие положения звеньев, их аналоги скоростей и ускорений в функции обобщенной координаты , можно, задаваясь величиной , определить скорости, ускорения и расположения звеньев в любом положении механизма.

Просмотров: 826

Вернуться в оглавление: Теория механизмов и машин