Степенные средние величины

Степенные средние величины получили свое название по виду функции, используемой для их расчета.
Если значения признаков в статистической совокупности не повторяются, степенную среднюю величину вычисляют в простой форме - это простая степенная средняя, при повторяющихся значениях – во взвешенной форме. Количество повторяющихся значений одного и того же признака ( Х i ) называется его весом (f i ).

Простая степенная средняя величина рассчитывается по формуле
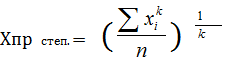, (6.1)

где k – показатель степени средней величины.

При k = - 1 по данной формуле рассчитывают гармоническую среднюю величину (Х гарм.).
Если 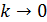, на основе теории пределов по данной формуле определяют геометрическую среднюю величину ( Х геом. ).

Далее при k = 1 находят арифметическую среднюю, при k = 2 - квадратическую , при k = 3 - кубическую, при k = 4 - биквадратическую и т.д.

Если одно и то же значение признака встречается несколько раз, рассчитывают взвешенную среднюю величину:

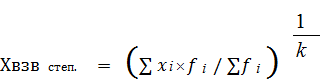, (6.2)
где f i - это вес (частота значений признака xi ).

Гармоническая средняя применяется если:
1 ) осредняемый признак является мерой времени и выражен в секундах и минутах.
2 ) осредняемая величина задана в виде функции неявного вида.
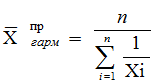,                                     (6.3)
где n – количество единиц в совокупности.

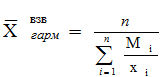,                                          (6.4)
где ,
Геометрическая средняя применяется при нахождении средних темпов или коэффициентов роста, т. к. она показывает во сколько раз в среднем одна величина в упорядоченной совокупности больше (или меньше) другой.
  = ,                     (6.5)
где n – число сомножителей (осредняемых значений признака).
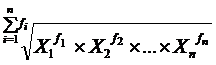  =       (6.6)
Арифметическая средняя определяется по формулам:
                                                 (6.7)
                                            (6.8)
Квадратическая средняя используется в тех случаях, когда осредняемая величина x задана в виде квадратической функции.
                                              (6.9)
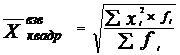                                         (6.10)
Кубическая средняя применяется, если осредняемая величина задана в виде квадратической функции.
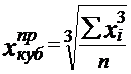                                                        (6.11)
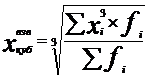                                (6.12)
Биквадратическая средняя рассчитывается как степенная средняя четвертого порядка и применяется при осреднении признака, являющегося функцией четвертого порядка.

Вернуться в оглавление: Статистика