Корреляционный метод анализа влияния факторов
Стохастические (корреляционные) связи. Стохастические связи проявляются в виде корреляции между значениями. Для их изучения применяются графический метод, метод сравнения параллельных рядов, метод аналитических группировок и регрессионно-корреляционный анализ.
Регрессионный анализ позволяет выявить вид связи, а корреляционный - установить тесноту (силу) связи.
Для линейных зависимостей теснота связи определяется с помощью коэффициента корреляции, а для нелинейных - с помощью индекса корреляции (корреляционного отношения).
Для расчета коэффициента корреляции используются различные формулы, но все они выводятся из одной и той же формулы.
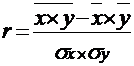 , (8.1)
, (8.1)
где ![]() и
и ![]() - среднеквадратические отклонения Х и У, рассчитанные по сгруппированным данным:
- среднеквадратические отклонения Х и У, рассчитанные по сгруппированным данным:
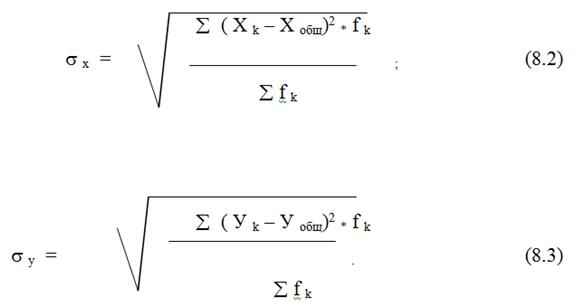
Теоретическое корреляционное отношение рассчитывают по формуле:
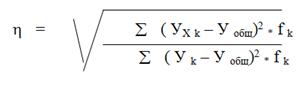 (8.4)
(8.4)
где УХ k - выравненные значения результативного признака, то есть рассчитанные по уравнению регрессии при Х = X к.
Значение r,n находится в пределах от -1 до +1 ![]()
Чем ближе значение r к единице, тем теснее связь W факторами х и у. Если эти коэффициенты < 0, это говорит об обратной связи между факторами х и у. Если х и у = 0, то связь между ними отсутствует.
Чтобы определить тесноту связи пользуются таблицей Чэддока.
При 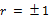 - связь функциональная.
- связь функциональная.
Корреляционное отношение являются более универсальным показателем, его можно рассчитывать и для линейных связей.
Для оценки тесноты связи между качественными показателями (например, работа по специальности, наличие жилья и т.п.) применяют непараметрические методы оценки корреляционной связи факторов. К непараметрическим методам относятся оценка связи на основе расчета коэффициентов ассоциации и контингенции. Для этого предварительно составляют таблицу, на пересечении строк и столбцов которой находятся числа, равные количеству единиц статистической совокупности с соответствующими значениями первого и второго признака.
Таблица 1 – Таблица значений качественных признаков
Первый признак |
Второй признак |
||
Первое значение |
Второе значение |
Итого |
|
Первое значение |
а |
b |
а+b |
Второе значение |
с |
d |
c+d |
Итого |
а+с |
b+d |
|
По итоговым данным таблицы 1 рассчитывают коэффициент ассоциации либо коэффициент контингенции:
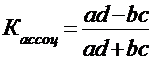 , (8.5)
, (8.5)
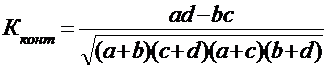 . (8.6)
. (8.6)
Если эти коэффициенты < 0.3, то связи между признаками нет.
Преимущество первого показателя состоит в том, что он единственный из всех показателей тесноты связи вполне определенно позволяет ответить на вопрос о характере связи между двумя признаками (прямопропорциональна она или обратнопропорциональна).
Зависимость между признаками может быть парной и многофакторной. В последнем случае на один и тот же признак у, оказывает влияние несколько факторных признаков, т.е. ![]() .
.
Просмотров: 3018
Вернуться в оглавление: Статистика