Понятие и виды рядов динамики

Ряд значений статистического показателя, расположенных в хронологическом порядке и характеризующих развитие явления во времени, называется рядом динамики. Динамический ряд состоит из двух элементов: момента или временного периода (t), по отношению к которому приводятся статистические данные, и статистического показателя, характеризующего размер рассматриваемого явления в соответствующий период времени, называемый уровнем динамического ряда (у).

В зависимости от того, в каких единицах выражены уровни ряда, ряды динамики бывают рядами абсолютных величин, относительных и средних величин.

По виду временного показателя динамические ряды бывают моментные и интервальные. Если уровни приводятся по состоянию на определенную дату, то такой ряд называют моментным рядом динамики. Моментные ряды динамики бывают с равноотстоящими уровнями и неравноотстоящими уровнями. В интервальных рядах динамики каждый уровень относится к определенному промежутку (интервалу) времени. Интервальные ряды динамики бывают с равными и неравными интервалами.

Вид ряда динамики влияет на выбор формул расчета его показателей.

Средний уровень ряда. Если дан моментный ряд с равными промежутками между датами, то для определения среднего уровня применяется формула средней хронологической взвешенной:

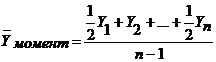(9.1)

Если в качестве уровней моментного динамического ряда взяты даты изменения показателя, то расчет среднего уровня следует проводить по формуле средней арифметической взвешенной, в качестве весов в которой используются временные промежутки между соседними датами.

Средний уровень интервального ряда при равных и неравных интервалах определяется соответственно по формулам:

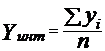, (9.2)

где yi = y j , i, j = 1, 2,…, n ,

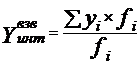, (9.3)
где fi- длина интервала для уровня yi и .

Абсолютный прирост– это разность между двумя уровнями ряда. Если сравнение происходит с одним и тем же уровнем ряда, то это базисные абсолютные приросты, если с предыдущим – цепные.

Средний абсолютный прирост рассчитывается по формуле:

                                  (9.4)
Средний коэффициент и темп роста равны:
,                                                                  (9.5)
                                    (9.6)

Средний коэффициент и темп прироста определяют соответственно:

, (9.7)
. (9.8)

Для двух рядов динамики рассчитывают коэффициент опережения:
, (9.9)

где уi1 и уiп - уровни первого и второго сравниваемых рядов динамики за один и тот же период (момент) времени.

Один процент абсолютного прироста ? 1 % ? рассчитывается по формуле:
. (9.10)

Вернуться в оглавление: Статистика