Методы проведения многомерной группировки

Многочисленные методы многомерной группировки (кластер-анализа) несмотря на имеющиеся различия вычислительных процедур, реализуются при последовательном выполнении общих алгоритмических шагов:

- формирование матрицы исходных данных (X) размере nх т, где п - число объектов наблюдения, т - число признаков, по которым производится группировка;

- переход от матрицы исходных данных к матрице нормированных данных (Z). Решение этой задачи означает, что разнородные по своей физической природе признаки приводятся к одному основанию, имеют одну и ту же условную единицу измерения. Переход осуществляется пересчетом значений группировочных признаков (хij) в zijпо одному из следующих вариантов:

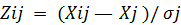(10.1)

Zij = Xij / Xj (эталон), (10.2)

Zij =Xij/Xjмах, (10.3)

Zij= Xij/Xjмах, (10.4)

Zij= (Xij - Xj )/(Xj мах- Xj мin). (10.5)

- определение расстояний между всеми парами наблюдаемых объектов (dij) и построение исходной матрицы расстояний (D0);

Для определения расстояний между объектами наблюдения, представляемых в теоретическом пространстве, существует набор метрик. Выбор метрики осуществляется самим исследователем.

С целью определения расстояний между объектами наблюдения кроме метрик расстояний могут использоваться и статистические меры сходства, как, например, коэффициенты парной корреляции, коэффициенты конкордации и т. д.;

- производится выбор конкретной процедуры кластер-анализа и по данным исходной матрицы расстояний (D0) последовательно выделяются группы однородных объектов. В настоящее время имеется достаточно большое количество различных процедур кластеризации данных, они объединяются в шесть основных семейств:
- иерархический кластер-анализ;
- итеративные методы группировки;
- методы поиска модальных значений плотности;
- факторные методы;
- методы поиска сгущений;
- методы, использующие теорию графов.

При помощи конкретного, отобранного заранее метода кластер-анализа выполняются вычислительные процедуры и получают разделение совокупности на кластеры (классы, группы):
- при помощи специальных показателей-функционалов оце-ниваются результаты кластер-анализа, в случае необходимости производится перегруппировка данных, улучшающая состав групп
с точки зрения однородности входящих в них объектов;
- на последнем шаге результаты кластер-анализа обобщаются при помощи графиков и таблиц и получают свою интерпре
тацию.

Перечисленных шагов может быть достаточно, если анализируются обычные признаки, имеющие количественную определенность. Если же в анализе участвуют ранговые (порядковые) или другие качественные характеристики, то приведенному выше алгоритму предшествуют этапы оцифровки неколичественных данных.

Из большого числа методов многомерной группировки в настоящее время наиболее широкое распространение получил иерархический кластерный анализ. Он может быть агломеративным и дивизимным.

В агломеративном кластер-анализе вначале каждый объект рассматривается как отдельный кластер, в последующем происходит их объединение до тех пор, пока все объекты не окажутся в одном кластере. В дивизимном кластер-анализе, наоборот, вначале вся совокупность объектов наблюдения — это один кластер, затем в ходе разделения совокупности приходят к состоянию, когда каждый объект рассматривается как отдельный кластер.

Однородные группы в иерархическом кластер-анализе определяются после графического представления результатов кластеризации в виде особенного графика — дендограммы.

Вернуться в оглавление: Статистика