Динамическое представление сигналов

Р Е Ф Е Р А Т на тему :

тАЬ Динамическое представление сигналов тАЬ

Выполнил: Зазимко С.А.

Принял : Котоусов А.С.

МОСКВА Динамическое представление сигналов.

Многие задачи радиотехники требуют специфической формы представления сигналов. Для решения этих задач необходимо располагать не только мгновенным значением сигнала, но и знать как он ведет себя во времени, знать его поведение в тАЬпрошломтАЭ и тАЬбудущемтАЭ.

ПРИНЦИП ДИНАМИЧЕСКОГО ПРЕДСТАВЛЕНИЯ.

Данный способ получения моделей сигналов заключается в следующем:

Реальный сигнал представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. Теперь, если мы устремим к нулю длительность отдельных элементарных сигналов, то в пределе получим точное представление исходного сигнала. Такой способ описания сигналов называется динамическим представлением , подчеркивая тем самым развивающийся во времени характер процесса.

На практике широкое применение нашли два способа динамического представления.

Первый способ в качестве элементарных сигналов использует ступенчатые функции, которые возникают через равные промежутки времени Δ . Высота каждой ступеньки равна приращению сигнала на интервале времени Δ. В результате сигнал может быть представлен как на рисунке 1.

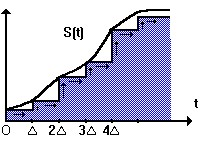
рис. 1

При втором способе элементарными сигналами служат прямоугольные импульсы. Эти импульсы непосредственно примыкают друг к другу и образуют последовательность, вписанную в кривую или описанную вокруг нее . В этом случае исходный сигнал имеет вид как на рисунке 2.

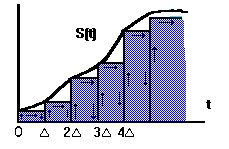
рис. 2

Теперь рассмотрим свойства элементарных сигналов. Для начала : используемого для динамического представления по первому способу.

ФУНКЦИЯ ВКЛЮЧЕНИЯ.

Допустим имеется сигнал, математическая модель которого выражается системой :

/ 0, t < -ξ,

u(t) = { 0.5(t/ξ+1), -ξ ≤ t ≤ ξ, (1)

\ 1, t > ξ.

Такая функция описывает процесс перехода некоторого физического объекта из тАЬнулевоготАЭ в тАЬединичноетАЭ состояние.

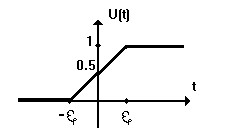
Переход совершается по линейному закону за время 2ξ. Теперь если параметр ξ устремить к нулю, то в пределе переход из одного состояния в другое будет происходить мгновенно. Такая математическая модель предельного сигнала получила название функции включения или функции Хевисайда :

/ 0, t < 0,

σ(t) = { 0.5, t = 0, (2)

\ 1, t > 0.

В общем случае функция включения может быть смещена относительно начала отсчета времени на величину t0. Запись смещенной функции такова :

/ 0, t < t0,

σ(t - t0) = { 0.5, t = t0, (3)

\ 1, t > t0.

ДИНАМИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПРОИЗВОЛЬНОГО СИГНАЛА ПОСРЕДСТВОМ ФУНКЦИЙ ВКЛЮЧЕНИЯ.

Рассмотрим некоторый сигнал S(t), причем для определенности скажем, что S(t)=0 при t<0. Пусть {Δ,2Δ,3Δ,..} - последовательность моментов времени и {S1,S2,S3,..} - отвечающая им последовательность значений сигнала. Если начальное значение сигнала есть S0=S(0), то текущее значение сигнала при любом t можно приближенно представить в виде суммы ступенчатых функций :

∞

s(t)≈s0σ(t)+(s1-s0)σ(t-Δ)+..=s0σ(t)+∑(sk-sk-1)σ(t-kΔ).

k=1

Если теперь шаг Δ устремить к нулю. то дискретную переменную kΔ можно заменить непрерывной переменной τ. При этом малые приращения значения сигнала превращаются в дифференциалы ds=(ds/dτ)dτ , и мы получаем формулу динамического представления произвольного сигнала посредством функций Хевисайда

∞

⌠ ds

S(t)=s0 σ(t) + | σ(t-τ) dτ (4)

⌡ dτ

Переходя ко второму способу динамического представления сигнала , когда элементами разложения служат короткие импульсы, следует ввести новое важное понятие - понятие дельта-функции.

ДЕЛЬТА - ФУНКЦИЯ .

Рассмотрим импульсный сигнал прямоугольной формы, заданный следующим образом :

1 / ξ ξ \

u(t;ξ) = ----- | σ (t + ---- ) - σ (t - ---- ) | (5)

ξ \ 2 2 /

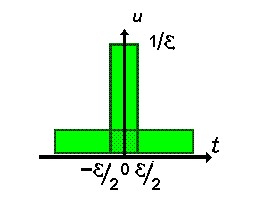
При любом выборе параметра ξ площадь этого импульса

равна единице :

∞

П = ∫ u dt = 1

- ∞

Например, если u - напряжение, то П = 1 В*с.

Теперь устремим величину ξ к нулю. Импульс, сокращаясь по длительности, сохраняет свою площадь, поэтому его высота должна неограниченно возрастать. Предел последовательности таких функций при ξ → 0 носит название дельта-функции , или функции Дирака1 :

δ(t) = lim u (t;ξ)

ξ→0

Дельта функция - интересный математический объект. Будучи равной нулю всюдю, кроме как в точке t = 0 2 дельта-функция тем не менее обладает единичным интегралом. А вот так выглядит символическое изображение дельта-функции :

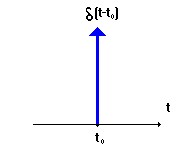
ДИНАМИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛА ПОСРЕДСТВОМ ДЕЛЬТА-ФУНКЦИЙ.

Теперь вернемся к задаче описания аналогового сигнала суммой примыкающих друг к другу прямоугольных импульсов (рис. 2) . С помощью дельта-функции u (t) представимо в виде совокупности примыкающих импульсов. Если Sk - значение сигнала на k - ом отсчете, то элементарный импульс с номером k представляется как :

ηk(t) = Sk [ σ(t - tk) - σ(t - tk - Δ) ] (6)

В соответствии с принципом динамического представления исходный сигнал S (t) должен рассматриваться как сумма таких элементарных слагаемых :

∞

S(t) = ∑ η (t) (7)

k= - ∞ k

В этой сумме отличным от нуля будет только один член, а именно тот, что удовлетворяет условию для t :

tk < t < tk+1

Теперь, если произвести подстановку формулы (6) в (7) предварительно разделив и умножив на величину шага Δ, то

∞ 1

S(t) = ∑ Sk --- [ σ(t - tk) - σ(t - tk - Δ) ] Δ

k=- ∞ Δ

Переходя к пределу при Δ → 0 , необходимо суммирование заменить интегрированием по формальной переменной τ, дифференциал которой dτ ,будет отвечать величине Δ .

Поскольку

lim [ σ(t - tk) - σ(t - tk - Δ) ] ---

Δ→0 Δ

получим искомую формулу динамического представления сигнала

∞

S (t) = ∫ s (τ) δ(t - τ) dτ

- ∞

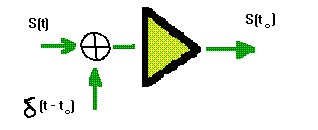
Итак, если непрерывную функцию умножить на дельта-функцию и произведение проинтегрировать по времени, то результат будет равен значению непрерывной функции в той точке, где сосредоточен δ - импульс. Принято говорить, что в этом состоит фильтрующее свойство дельта-функции.3

Из определения дельта-функции следует (3) . Следовательно, интеграл дельта-функции от - ∞ до t есть единичный скачок , и дельта-функцию можно рассматривать как производную единичного скачка :

δ(t) = 1тАЩ (t) ;

δ(t-t0) = 1тАЩ (t-t0) .

Обобщенные функции как математические модели сигналов.

В классической математике полагают, что функция S(t) должна принемать какие-то значения в каждой точке оси t . Однако рассмотренная функция δ(t) не вписывается в эти рамки - ее значение при t = 0 не определено вообще, хотя эта функция и имеет единичный интеграл. Возникает необходимость расширить понятие функции как математической модели сигнала. Для этого в математике была введено принципиально новое понятие обобщенной функции.

В основе идеи обобщенной функции лежит простое интуитивное соображение. Когда мы держим в руках какой-нибудь предмет , то стараемся изучить его со всех сторон, как бы получить проекции этого предмета на всевозможные плоскости. Аналогом проекции исследуемой функции ƒ(t) может служить, например, значение интеграла

∞

∫ ƒ(t) φ(t) dt (8)

- ∞

при известной функции φ(t) , которую называют пробной функцией.

Каждой функции φ(t) отвечает, в свою очередь, некоторое конкретное числовое значение. Поэтому говорят, что формула (8) задает некоторый функционал на множестве пробных функций φ(t). Непосредственно видно, что данный функционал линеен, то есть

(ƒ, αφ1 + βφ2) = α(ƒ,φ1) + β(ƒ,φ2).

Если этот функционал к тому же еще и непрерывен, то говорят, что на множестве пробных функций φ(t) задана обобщенная функция ƒ(t) 4

. Следует сказать, что данную функцию надо понимать формально-аксиоматически, а не как предел соответствующих интегральных сумм.

Обобщенные фнкции , даже не заданные явными выражениями, обладают многими свойствами классических функкций. Так, обобщенные функции можно дифференцировать.

И в заключение следует сказать, что в настоящее время теория обобщенных функций получила широкое развитие и многочисленные применения. На ее основе созданы математические методы изучения процессов, для которых средства классического анализа оказываются недостаточными.

Литература :

1. А. Л. Зиновьев, Л. И. Филипов ВВЕДЕНИЕ В

ТЕОРИЮ СИГНАЛОВ И ЦЕПЕЙ.

2. С. И. Баскаков РАДИОТЕХНИЧЕСКИЕ ЦЕПИ

И СИГНАЛЫ.

1 Также эту функцию называют единичной импульсной функцией,

2 Говорят, что дельта-функция сосредоточена в этой точке.

3 Отсюда вытекает структурная схема систем, осуществляющей измерение мгновенных значений аналогового сигнала S(t). Система состоит из двух звеньев : перемножителя и интегратора.

4 Обобщенные функции иногда называют также распределениями.

Вместе с этим смотрят:

Дисковод CD-ROM
Единицы измерения количества информации
Единицы информации
Единое информационное пространство в России