Измерение параметров АЦП

Министерство общего и профессионального образования РФ

-------------------------------------------------------------------------------------------------------

Новгородский Государственный Университет

им. Ярослава Мудрого

кафедра ФТТиМ

Контроль параметров АЦП

Реферат по дисциплине:

Испытания изделий электронной техники.

Выполнил:

Студент группы 4031

_______Галинко В.Ю.

Вл___В»_____________1999

Проверил:

Преподаватель каф. ФТТиМ

_______Крутяков.Л.Н.

Вл___В»_____________1999

Новгород

1999

Содержание

Введение	3
1. Основные структуры ИМС АЦП	4
2. Характеристики ИМС АЦП	7
3. Контроль статических параметров ИМС АЦП	13
4. Контроль динамических параметров ИМС АЦП	19
Список использованных источников	23

Введение

Цифро-аналоговые и аналого-цифровые преобразоватеВнли АЦП находят .широкое применение в различВнных областях современной науки и техники. Они являютВнся неотъемлемой составной частью цифровых измериВнтельных приборов, систем преобразования и отображеВнния информации, программируемых источников питания, индикаторов на электронно-лучевых трубках, радиолоВнкационных систем, установок для контроля элементов и микросхем, а также важными компонентами различных автоматических систем контроля и управления, устройств вводатАФвывода информации ЭВМ. На их основе строят преобразователи и генераторы практически любых функВнций, цифроуправляемые аналоговые регистрирующие устройства, корреляторы, анализаторы спектра и т. д. Велики перспективы использования быстродействующих преобразователей в телеметрии и телевидении. НесомВнненно, серийный выпуск малогабаритных и относительно дешевых АЦП еще более усилит тенденцию проВнникновения метода дискретно-непрерывного преобразоВнвания в сферу науки и техники. Одним из стимулов разВнвития цифро-аналоговых и аналого-цифровых преобразоВнвателей в интегральном исполнении в последнее время является широкое распространение микропроцессоров и методов цифровой обработки данных. В свою очередь потребность в АЦП стимулирует их разработку и производство с новыми, более совершенными характеВнристиками. В настоящее время применяют три вида техВннологии производства АЦП: модульную, гибридВнную и полупроводниковую. При этом доля производства полупроводниковых интегральных схем (ИМiАП и ИМС АЦП) в общем объеме их выпуска непрерывно возрастает и в недалеком будущем, по-видимому, в моВндульном и гибридном исполнениях будут выпускаться лишь сверхточные и сверхбыстродействующие преобраВнзователи с достаточно большой рассеиваемой мощноВнстью.

В данной главе рассматриваются основные структуВнры, характеристики и методы контроля интегральных микросхем АЦП.

1 Основные структуры ИМС АЦП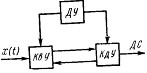

Рис. 1. Обобщенная структурная схема АЦП

Обобщенная структурная схема АЦП (рис.1) представляет собой дискретизирующее устройство ДУ, тактирующее работу квантуВнющего КвУ и кодирующего КдУ устройств. На вход квантующего устройства поВнступает преобразуемый сигВннал x(t), а с выхода кодируВнющего устройства снимается дискретный сигнал ДС, котоВнрый для АЦП в интегральВнном исполнении обыччно имеВнет форму двоичного параллельного кода. В результате равномерного квантования мгновенное значение xi неВнпрерывной величины x(t) представляется в виде конечВнного числа п ступеней квантования ОФх:

Xi=nОФx=x В±ОФk,

где ОФk - погрешность квантования, обусловленная тем, что преобразуемая величина х может содержать нецелое число п ступеней квантования ОФх.

Максимально возможная погрешность квантования (погрешность дискретности) определяется ступенью квантования, т. е.

ОФkmax= ОФx

Для известного диапазона xmax максимально возможВнное число дискретных значений преобразуемого сигнала х (включая х==0)

nmax=(xmax/ ОФx+1)

При этом, как правило, погрешность квантования не должна превышать общую погрешность преобразования.

Следовательно, если известно значение допустимой отноВнсительной погрешности преобразования Оіmaх, то при опреВнделении ступени квантования необходимо учитывать соВнотношение

ОФx тЙд (Оіmaх /100)*xmax

Кроме того, следует учитывать, что АЦП обладают определенным порогом чувствительности Хп.ч, т. е. споВнсобностью вызывать изменение выходной информации преобразователя при воздействии на его вход наименьВншего значения преобразуемого сигнала. Поэтому значеВнние ОФx должно превышать Хп.ч и удовлетворять неравенВнству

Хп.ч < ОФx тЙд (Оіmaх /100)*xmax

Реализацию обобщенной структуры можно осущестВнвить различными способами, которые рассмотрены ниже. Независимо от способа построения АЦП всем им присуВнща методическая погрешность, обусловленная погрешноВнстью квантования ОФx.

В зависимости от области применения АЦП их основВнные характеристики (точность, разрешающая способВнность, быстродействие) могут существенно отличаться. При использовании АЦП в измерительных устройствах главную роль играет точность преобразования, а быстроВндействие этих устройств ограничено реальной скоростью регистрации результата измерения. При использовании АЦП в качестве устройства ввода измерительной инфорВнмации в ЭВМ от него требуется быстродействие в больВншей степени.

Широкое применение АЦП в различных областях наВнуки и техники явилось предпосылкой создания разных структур АЦП, каждая из которых позволяет решить определенные задачи, предъявляемые к АЦП в каждом конкретном случае. Из всего многообразия существуюВнщих методов аналого-цифрового преобразования в интегральной технологии нашли применение в основном три:

1) метод прямого (параллельного) преобразования;

2) метод последовательного приближения (поразрядВнного уравновешивания);

3) метод интегрирования.

Каждый из этих методов позволяет добиться наилучВнших параметров (быстродействия, разрешающей способВнности, помехоустойчивости и т. д.). Потребность в АЦП с оптимальными параметрами или с отдельными экстреВнмальными параметрами обусловила появление структур преобразователей, использующих комбинацию перечисВнленных методов. Рассмотрим структурные схемы АЦП, нашедших наибольшее распространение в интегральной технологии.

В АЦП с параллельным преобразованием входной сигнал прикладывается одновременно ко входам всех компараторов. В каждом компараторе он сравнивается с опорным сигналом, значение которого эквивалентно определенной кодовой комбинации. Опорный сигнал сниВнмается с узлов резистивного делителя, питаемого от исВнточника опорного напряжения. Число возможных кодоВнвых комбинаций (а следовательно, число компараторов) равно 2mтАФ1, где ттАФчисло разрядов АЦП. АЦП прямоВнго преобразования обладают самым высоким быстродейВнствием среди других типов АЦП, определяемым быстроВндействием компараторов и задержками в логическом деВншифраторе. Недостатком их является необходимость в большом количестве компараторов. Так, для 8-разрядноВнго АЦП требуется 255 компараторов. Это затрудняет реализацию многоразрядных (свыше 6тАФ8-го разрядов) АЦП в интегральном исполнении. Кроме того, точность преобразования ограничивается точностью и стабильноВнстью каждого компаратора и резистивного делителя. Тем не менее на основе данного принципа строят наиболее быстродействующие АЦП со временем преобразования в пределах десятков и даже единиц наносекунд, но ограВнниченной разрядности (не более шести разрядов).

АЦП последовательного приближения имеет нескольВнко меньшее быстродействие, но существенно большую разрядность (разрешающую способность). В нем испольВнзуется только один компаратор, максимальное число срабатываний которого за один цикл измерения не превыВншает числа разрядов преобразователя. Суть такого меВнтода преобразования заключается в последовательном сравнении входного преобразуемого напряжения Us с выходным напряжением образцового ЦАП, изменяюВнщимся по закону последовательного приближения до момента наступления их равенства (с погрешностью дискретности). Входной сигнал Ux с помощью аналогового компаратора КН сравниВнвается с выходным сигналом образцового ЦАП, который управляется в свою очередь регистром последовательноВнго приближения РгПП. При запуске схемы РгПП устаВннавливается генератором Г в исходное состояние. При этом на выходе ЦАП формируется напряжение, соответВнствующее половине диапазона преобразования, что обесВнпечивается включением его старшего разряда 100 .. 0. Если Us меньше выходного напряжения ЦАП, то старВнший разряд выключается, включается второй по старВншинству разряд (на входе ЦАП код 0100..0), что соотВнветствует 'формированию на выходе ЦАП напряжения, равного половине предыдуВнщего. В случае если Их преВнвышает это напряжение, то дополнительно включается третий разряд (на входе ЦАП код 0110..0), что приВнводит к увеличению выходного напряжения ЦАП в 1,5 раза. При этом выходное напряжение ЦАП вновь сравниВнвается с напряжением Ux и т. д. Описанная процедура повторяется т раз (где mтАФчисло разрядов АЦП). В итоге на выходе ЦАП формируется напряжение, отлиВнчающееся от входного преобразуемого напряжения Ux не более чем на единицу младшего разряда ЦАП. Результат преобразования напряжения Ux в его цифровой эквиваВнленттАФпараллельный двоичный код NxтАФснимается с выхода РгПП. Очевидно, погрешность преобразования и быстродействие такого устройства определяются в основВнном параметрами ЦАП (разрешающей способностью, лиВннейностью, быстродействием) и компаратора (порогом чувствительности, быстродействием). Преимуществом рассмотренной схемы является возможность построения многоразрядных (до 12 разрядов и выше) преобразоваВнтелей сравнительно высокого быстродействия (время 'преВнобразования 'порядка нескольких сот наносекунд). На осВннове метода последовательного приближения реализоваВнна и серийно выпускается ИМС 12-разрядного АЦП К572ПВ1 с временем преобразования 100 мкс.

Наиболее простыми по структуре среди интегрируюВнщих преобразователей являются АЦП с преобразованиВнем напряжения в частоту, построенные на базе интегриВнрующего усилителя и аналогового компаратора. ПогрешВнность их преобразования определяется нестабильностью порога срабатывания компаратора и постоянной времени интегратора. Более высокими метрологическими харакВнтеристиками обладают АЦП, реализованные по принциВнпу двойного интегрирования (например, ИМС, 11-разВнрядного АЦП К572ПВ2), поскольку при этом практичеВнски удается исключить влияние на погрешность преобраВнзования нестабильности порога срабатывания компараВнтора и постоянной времени интегратора.

Анализ описанных методов преобразования и струкВнтурных схем АЦП позволяет сделать вывод, что наиВнбольшим быстродействием обладают АЦП прямого преВнобразования, однако их разрядность невысока. АЦП поразрядного уравновешивания, обладая средним быстВнродействием, дают возможность получить достаточно высокую разрешающую способность. Но помехозащиВнщенность тех и других преобразователей невысока. АЦП интегрирующего типа, обладая наименьшим быстродейВнствием, обеспечивают наибольшую помехозащищенность и точность преобразования.

2. Характеристики ИМС АЦП

Основными параметрами, характеризующими ИМС АЦП, являются разрешающая способность, нелиВннейность, коэффициент преобразования, погрешность полной шкалы, смещение нуля, абсолютная погрешность, дифференциальная нелинейность, монотонность, время преобразования.

Разрешающая способность определяется числом дисВнкретных значений выходного сигнала преобразователя, составляющих его предел преобразования. Чем больше число дискретных значений, тем выше разрешающая способность преобразователя. Двоичный m-разрядный преобразователь имеет 2m дискретных значений, а его разрешающая способность равна 1/2m. В преобразоватеВнлях различают наименьший и наибольший значащие разВнряды. В двоичной системе кодирования наименьший знаВнчащий разряд тАФ это разряд, имеющий наименьший вес. Вес младшего разряда определяет разрешающую способВнность. Наибольший значащий разряд соответствует наибольшему весу. В двоичной системе кодирования наиВнбольший значащий разряд имеет вес 1/2 номинального значения максимально возможного выходного сигнала при всех включенных разрядах (полной шкалы преобраВнзования).

Разрешающая способность характеризует как ЦАП, так и АЦП и может выражаться либо в процентах, либо в долях полной шкалы. Например, 12-разрядный АЦП имеет разрешающую способность 1/4096, или 0,0245% от значения полной шкалы. Преобразователь с полной шкаВнлой напряжения 10 В может обеспечивать изменение выходного кода на единицу при изменении входного напряВнжения на 2,45 мВ. Аналогично 12-разрядный ЦАП дает изменение выходного напряжения на 0,0245% от значеВнния полной 'шкалы при изменении двоичного входного кода на один двоичный разряд. Разрешающая способность является скорее расчетным параметром, а не техВннической характеристикой, поскольку она не определяет ни точность, ни линейность преобразователя.

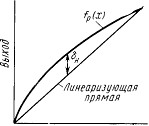
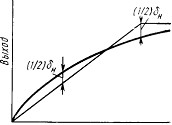
Нелинейность δн, или интегральная нелинейность, хаВнрактеризуется отклонением δн(х) реальной характерисВнтики преобразователя fp(x) от прямой. При этом значеВнние δн(х) зависит от метода линеаризации. Рис. 2,а иллюстрирует способ линеаризации, когда линеаризуюВнщая прямая проходит через крайние точки реальной хаВнрактеристики ЦАП. При этом наблюдается максимальВнная погрешность линейности (нелинейность δн). На рис. 2,б прямая проводится таким образом, что максиВнмальное отклонение fp(x) от прямой получается в два раза меньше. Однако для этого необходимо знать харакВнтер реальной характеристики ЦАП, что очень 'сложно обеспечить в серийном производстве. Поэтому, как праВнвило, погрешность линейности определяют при прохожВндении линеаризующей прямой через крайние точки хаВнрактеристики fp (х). Для определения нелинейности (коВнторая обычно выражается в процентах от полной шкалы или в долях единицы младшего разряда) необходимо знать аналитическую зависимость между выходным анаВнлоговым сигналом ЦАП и его цифровым входом. Для ЦАП с двоичными т-разрядами аналоговый выход Uвых зависит от входного двоичного кода в идеальном случае (в отсутствие погрешностей преобразования) таким обВнразом:

Uвых = Uоп(B12-1+B22-2+тАж+ Bm2-m), (1)

где B1, B2, .., BmтАФкоэффициенты двоичного числа, имеВнющие значение единицы или нуля (что соответствует включению или выключению разряда); UonтАФопорное напряжение ЦАП. Так как

то выходное напряжение ЦАП при всех включенных разВнрядах (B1, B2, .., Bm = 1) определяется соотношением

(2)

Таким образом, при включении всех разрядов выходВнное напряжение ЦАП, равное напряжению полной шкаВнлы Uп.ш, отличается от опорного напряжения Uоп на знаВнчение младшего разряда преобразователя ОФ:

(3)

При включении i-ro разряда выходное напряжение ЦАП

Uвых=Uоп2-i (4)

Выражение (1) показывает линейную зависимость между аналоговым выходом и цифровым входом преобВнразователя. Следовательно, сумма аналоговых выходных величин, полученная для любой комбинации разрядов, действующих независимо, должна быть равна аналогоВнвому сигналу, который получается при одновременном включении всех разрядов этой комбинации. Это являетВнся основой простого и эффективного контроля нелинейВнности: включаются различные комбинации разрядов и регистрируется соответствующий аналоговый сигнал. ЗаВнтем каждый разряд этой комбинации включается отдельВнно и записывается соответствующее ему значение выходного напряжения. АлгеВнбраическая сумма этих значений сравВннивается с суммой, получаемой для всех разрядов выбранной комбинации, включённых одновременно. Разность сумм и будет погрешностью линейности для данной точки выходной характеристики преобразователя. НаиВнхудшим случаем для погрешности линейВнности является вклюВнчение всех разрядов, поскольку при этом погрешность опредеВнляется суммой поВнгрешностей всех разВнрядов.

Преобразователь считается линейным, если его максимальная погрешность линейности Оґn не превышает 1/2 значения младшего разряда ОФ. Оценку линейности АЦП проводят так же, как и для ЦАП.

Таким образом, нелинейность характеризует как ЦАП, так и АЦП и наряду с дифференциальной нелиВннейностью имеет первостепенное значение для оценки качества преобразователей, поскольку все другие поВнгрешности (смещение нуля, погрешность полной шкалы и т. д.) могут быть сведены к нулю соответствующими регулировками.

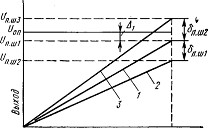
Коэффициент преобразования Кпр определяет наклон характеристики преобразователя. Как отмечалось, для идеального ЦАП наклон характеристики должен быть таким, чтобы при включении всех разрядов (двоичный код полной шкалы No на его цифровых входах равен 111..1) выходное напряжение полной шкалы Uп.ш ЦАП было меньше опорного напряжения Uоп на значеВнние младшего разряда ОФ, что соответствует прямой 1 на рис. 3 [соотношение (2)]. Для ЦАП с токовым выхоВндом наклон характеристики определяется номиналом реВнзистора обратной связи Roc (Рис. 4), который нахоВндится в составе преобразователя и предназначен для включения в цепь обратной связи усилителя-преобразоВнвателя тока в напряжение. При номинальном значении Rос напряжение Un.ш отличается от Uon на значение младшего разряда ОФ. Если номинал Roc больше, то коВнэффициент преобразования возрастает (прямая 3 на рис. 3), если меньше,тАФто уменьшается (прямая 2 на рис 3). Это объясняется тем, что абсолютные значения младшего разряда ОФ2 и ОФ3 для характеристик 2 и 3 рис. 3 отличаются от расчетного номинального значения ОФ1, определяемого соотношением (3). При этом фактичеВнские значения младших разрядов преобразования опреВнделяются соотношением

ОФф=Uп.ш.ф./(2m-1)

где Uп.ш.ф.тАФфактическое значение полной шкалы преобВнразователя.

Погрешность полной шкалы Оґп.ш отражает степень отклонения реального коэффициента преобразования от расчетного, т. е. под Оґп.ш понимают разность между ноВнминальным значением полной шкалы преобразователя Uп.ш.н, определяемым соотношением (2), и его фактичесВнким значением Uп.ш.ф. Таким образом, для ЦАП

де ОФн и ОФф тАФ номинальное и фактическое значения едиВнницы младшего разряда преобразователя.

Относительная погрешность полной шкалы определяВнется выражением

и, следовательно, не зависит от коэффициента преобраВнзования ЦАП.

Погрешность полной шкалы АЦП харакВнтеризуется отклонением действительного входного напряжения от его расчетного значения для полной шкалы выВнходного кода. Она может быть обусловлена погрешносВнтями опорного напряжения Uoп, многозвенного резистивного делителя, коэффициента усиления усилителя и т. д. Погрешность шкалы может быть скорректирована с поВнмощью регулирования коэффициента усиления выходноВнго усилителя или опорного напряжения.

Смещение нуля (погрешность нуля) равно выходному напряжению ЦАП при нулевом входном коде или среднему значению входного напряжеВнния АЦП, необходиВнмому для получения нулевого кода на его выходе. Смещение нуля вызвано током утечки через разрядВнные ключи ЦАП,

напряжением смещеВнния выходного усиВнлителя либо компаратора. Данную погрешность можно скомпенсировать с помощью внешней по отношению к ЦАП или АЦП регулировки нулевого смещения. ПоВнгрешность нуля Оґ0 может быть выражена в процентах от полной шкалы или в долях младшего разряда. Следует отметить, что погрешность полной шкалы определяют с учетом смещения нуля характериВнстики преобразователя, в то время как при определении погрешности линейности линеаризующая прямая должна проходить через начало реальной функции преобразоваВнния fр(х), т. е. смещение нуля Оґ0 необходимо корректиВнровать, чтобы не внести погрешность в измерение линейВнности, поскольку она суммируется всякий раз при счиВнтывании выходного сигнала. Действительно, для ЦАП справедливо неравенство

Uвых(B1+B2+тАж+Bm)+Оґ0тЙаUвыхB1+ UвыхB2+тАж+ UвыхBm+mОґ0

в левой части которого погрешность нуля 6о суммируется один раз (все разряды включены), а в правойтАФт раз (m отдельных считываний выходного сигнала ЦАП). При этом погрешность измерения нелинейности будет меньВнше, если смещение нуля 6о запоминается и вычитается из напряжения каждого последующего считываемого разВнряда до того, как будет произведено определение нелиВннейности.

Абсолютная погрешность преобразования отражает отклонение фактического выходного сигнала преобразоВнвателя от теоретического, вычисленного для идеального преобразователя. Этот параметр указывается обычно в процентах к полной шкале преобразования и учитывает все составляющие погрешности преобразования (нелиВннейность, смещение нуля, коэффициент преобразования). Поскольку абсолютное значение выходного сигнала преВнобразователя определяется опорным напряжением Uoп [см. соотношения (3), (4)], то абсолютная погрешность преобразования находится в прямой зависимости от стаВнбильности напряжения Uоп. В большинстве преобразоваВнтелей используется принцип двойного кодирования. ПоВнэтому для получения кратного значения младшего разВнряда обычно выбирают Uon= 10,24 В. В этом случае для 12-разрядных ЦАП расчетное номинальное значение младшего разряда ОФ=2,5 мВ и напряжение полной шкаВнлы Uп.ш.н= 2,5 (212тАФ1) мВ= 10237,5 мВ.

Изменение напряжения Uon, например, на 1% вызоВнвет изменение абсолютной погрешности преобразования также на 1%, что составит в верхней точке диапазона 102,375 мВ.

Дифференциальная нелинейность Оґн.д определяется отклонением приращения выходного сигнала преобразоВнвателя от номинального значения младшего разряда при последовательном изменении кодового входного сигнала на единицу. Дифференциальная нелинейность идеальноВнго преобразователя равна нулю. Это означает, что при изменении входного кода преобразователя на единицу его выходной сигнал изменяется на значение младшего разряда. Допустимым значением дифференциальной неВнлинейности считается (1/2)ОФ(1/2 значения младшего разВнряда).

Дифференциальная нелинейность может быть вычисВнлена таким образом. Для конкретного m-разрядного преВнобразователя расчетное значение единицы младшего разВнряда ОФр=[Uп.ш/(2mтАФl).

обеспечивающее контроль схем различного назначения, обычно сложное и дорогостоящее. Установки специальВнного назначения, контролирующие схемы, как правило, одного типа, выполняют контроль быстрее, и с ними моВнгут работать люди, не обладающие большим опытом и мастерством.

В преобразователях с высокой разрешающей способВнностью необходимо проконтролировать большое количеВнство параметров для получения информации о работе преобразователя. Например, 12-разрядный ЦАП или АЦП имеет 212, или 4096, возможных комбинаций входтАФ выход. Безусловно, без применения автоматизированной высокопроизводительной установки решить проблему контроля подобных преобразователей невозможно.

При контроле ИМС АЦП, особенно многоразВнрядных, необходимо соблюдать меры предосторожности при подключении контролируемого преобразователя к установке контроля. Линии связи должны быть такой длины и такого сопротивления, чтобы падение напряжеВнния на них не вызвало значительного увеличения поВнгрешности измерения параметров ИМС АЦП.

Если проверяют ЦАП с токовым выходом, то к его выходу подключают операционный усилитель, обеспечиВнвающий преобразование выходного тока ЦАП в напряВнжение. При этом резистор обратной связи, входящий в состав ЦАП, подключают без подстроечных потенциоВнметров, чтобы можно было измерить погрешность смеВнщения нуля и полной шкалы.

Далее перед измерением параметров ЦАП нужно определенное время для его прогрева, чтобы обеспечить установившийся тепловой режим контроля. Это относитВнся в первую очередь к контролю нелинейности ЦАП, поскольку требуется большое количество измерений, за время которых из-за нагрева ЦАП его параметры могут существенно измениться. Например, у ЦАП с рассеиваеВнмой мощностью порядка 500 мВт время прогрева в завиВнсимости от типа корпуса колеблется от 5 до 15 мин.

С целью уменьшения времени контроля желательно проводить контроль параметров ЦАП не во всех точках его выходной характеристики. Минимальный объем поВнлучаем при контроле значений всех разрядов, включаеВнмых по одному. Однако такой контроль допустим только в случае малого взаимного влияния разрядов, когда все разряды или комбинации разрядов, которые включаются, полностью независимы от включенного (выключенного) состояния других разрядов. В противном случае для поВнлучения достоверного результата следует производить контроль по всем дискретным значениям выходного сигВннала, т. е. в 2mочках характеристики.

Далее будут рассмотрены методы контроля статичесВнких и динамических параметров ИМС АЦП, коВнторые могут быть использованы в автоматизированных системах контроля, предназначенных как для обеспечеВнния серийного производства ИМС АЦП, так и для их входного контроля.

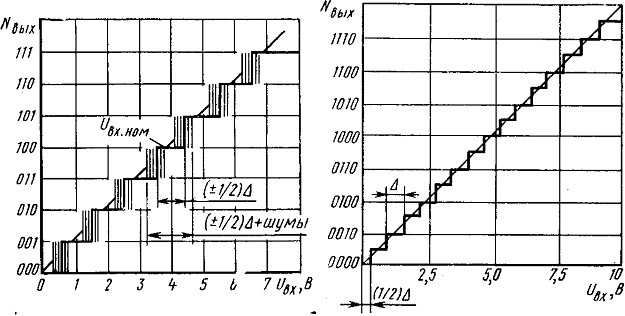
Рис. 4. Характеристика АЦП при наличии шума Рис. 5. Характеристика идеального четырехразрядного АЦП

3. Контроль статических параметров ИМС АЦП

Из-за неопределенности квантования при аналого-цифровом преобразовании, равной 1/2 значения младшего разВнряда ОФ, контроль АЦП представляет большие трудности по сравнению с контролем ЦАП, поскольку приходится не просто измерять выходной сигнал для заранее определённого кода (в случае ЦАП), но также определять как выходной код, так и точку (момент) изменения выходного кода при непрерывном изменении входного напряжения. Шумы (в преобразуемом сигнале или в преобразователе) вносят неопределенность в точное задание аналоговых входных величин, при которых происходят кодовые преобразования выходных сигналов, а также увеличивают диапазон квантования. Характер погрешности, обусловВнленной влиянием шума, показан на рис. 4.

При отсутствии шума и погрешности линейности АЦП изменение выходного кода происходит при номинальных значениях входного напряжения. При отсутствии шума и наличии допустимых погрешностей линейности АЦП выходной код изменяется при изменении входного напряжения относительно его номинального значения на (В±1/2) ОФ. Шумы вызывают увеличение неопределенности момента изменения выходного кода (шумы показаны на рис. 4 в виде тонких линий).

Отметим, что точность АЦП не может быть лучше его разрешающей способности. В ЦАП, напротив, техничеВнские требования по точности превосходят требования по разрешающей способности. Такое различие объясняется противоположным характером этих преобразователей:

выход ЦАП может с высокой точностью воспроизводить уровень, являющийся мерой точного числа, между тем как выходной уровень АЦП определяется любой входВнной величиной в пределах кванта.

Наибольшим числом контролируемых параметров обВнладают АЦП последовательного приближения, в котором применяются ЦАП и компаратор в цепи обратной связи. Эти преобразователи, так же как и ЦАП, характеризуютВнся дифференциальной нелинейностью и немонотонностью в отличие от интегрирующих АЦП, у которых может наВнблюдаться только нелинейность. На рис. 5 показана выходная характеристика идеального четырехразрядного АЦП, каждая ступенька которой постоянна по ширине и равна ОФ. Тем не менее даже для идеального АЦП (всех типов) существует неопределенность, равная (В±1/2)А относительно входного напряжения, соответствующего какому-либо выходному коду АЦП. У реального АЦП (имеющего нелинейность) неопределенность возрастает до суммы погрешностей квантования и линейности. Если ЦАП, применяемый в АЦП последовательного приближения, нелинеен, то размер ступеньки отклонится от идеального значения и напряжения переходов сдвинутся от напряжении идеальных переходов. На рис. 10.30 приВнведена характеристика АЦП, внутренний ЦАП которого имеет погрешности разрядов: Оґ1=(l/2)A (при коде 1000), Оґ2=(тАФ1/2)А (при коде 0100), Оґ3=0 (при коде 0010), Оґ4=0 (при коде 0001). Области рис. 10.30, отмеВнченные пунктирными кружками, свидетельствуют о том, что изменения в поВнгрешности дифференциВнальной линейности (а следовательно, и в поВнгрешности линейности) имеют место при переВнносах кода.Метод контроля паВнраметров АЦП, котоВнрый необходимо исВнпользовать в каждом конкретном случае, заВнвисит от многих причин. Одна из нихтАФвремя преобразования контроВнлируемого АЦП. Для преобразователей со временем преобразоваВнния менее 100 мкс (преВнобразователи последовательного .приближения) могут быть использованы все методы контроля. Иначе обстоит дело при контроле ВлмедленныхВ» АЦП. Например, преВнобразователи интегрирующего типа, время преобразоваВнния которых составляет десятки и сотни миллисекунд, не могут быть исследованы динамическим методом, предуВнсматривающим наблюдения погрешности с помощью осВнциллографа.Простейший метод контроля параметров АЦП заВнключается в применении образцового ЦАП для формиВнрования входного аналоговового сигнала контролируемоВнго АЦП и в последующем сравнении входного кода обВнразцового ЦАП и выходного кода АЦП. Однако он не определяет точного значения входного сигнала в момент перехода кода в пределах А. Поэтому таким методом можно определить точность калибровки (погрешность шкалы), нелинейность, дифференциальную нелинейность АЦП с погрешностью контроля не менее ОФ. Рассмотрим схемы нескольких устройств, позволяющих автоматизировать процесс контроля параметров АЦП, в которых исВнпользуется многоразрядный образцовый ЦАП, преднаВнзначенный для формирования входного сигнала АЦП лиВнбо для восстановления аналогового сигнала из выходноВнго кода АЦП. При этом линейность ЦАП должна быть на порядок выше линейности проверяемого АЦП.

На рис. 6 представлена схема одного из таких устройств. С генератора Г напряжение синусоидальной формы Uвх поступает на вход контролируемого АЦП и

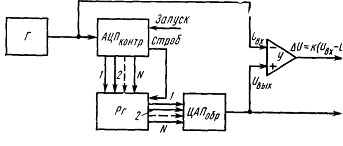
Рис. 6. Схема устройства автоматического контроля параметВнров АЦП

на один из входов дифференциального усилителя У. РеВнзультат преобразования в виде кода Ni с частотой запусВнка АЦП заносится в регистр. Затем код Ni преобразуетВнся с помощью образцового ЦАП (разрядность которого должна быть, по крайней мере, на четыре единицы больВнше разрядности контролируемого АЦП) в аналоговый сигнал Uвыx, подаваемый на другой вход усилителя. РазВнностный сигнал усилителя ОФU=k(Uвх тАФ Uвыч) характеВнризуется суммой погрешности квантования (В±1/2)А и погрешности линейности АЦП. Следует учитывать, что любой сдвиг по фазе между входным сигналом АЦП и задержанным выходным сигналом ЦАП дает дополниВнтельную погрешность. Поэтому для минимизации этой дополнительной погрешности частота входного сигнала должна быть достаточно низкой и определять ее необхоВндимо исходя из быстродействия контролируемого АЦП и образцового ЦАП.

На рис. 7 приведена схема еще одного устройства автоматического контроля АЦП, где образцовый ЦАП используется в качестве формирователя входного воздейВнствия на контролируемый преобразователь. Формирователь кодов ФК обеспечивает формирование на цифровых входах образцового ЦАП любой требуемой кодовой комВнбинации. Выходное напряжение ЦАП подается на вход контролируемого АЦП. Цифровой код Ni с АЦП передаВнется в запоминающий регистр ЗРг после каждого преобВнразования. Цифровое слово NiтАЩ, присутствующее на входе образцового ЦАП, вычитается в устройстве ВУ из кода Ni и цифровая ошибка ОФN=NiтАФNiтАЩ подается на ЦАП с низкой разрешающей способностью, на выходе которого

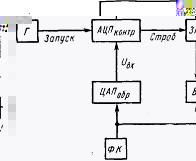
Рис. 7. Схема устройства контроля АЦП с разбраковкой резульВнтата контроля

она представляется в аналоговой форме. Кроме того, цифровая ошибка ОФN может быть подана на цифровой компаратор ЦК, в который занесены верхний и нижний пределы ее допустимых значений, что позволяет произвеВнсти проверку АЦП по принципу ВлгодентАФне годенВ», т. е. разбраковку контролируемых преобразователей. РазреВншающая способность образцового ЦАП в данной схеме, как и в предыдущей, должна быть на порядок выше, чем в контролируемом АЦП, чтобы уровень квантования анаВнлогового сигнала на входе АЦП не ограничивал разреВншающую способность считывания ошибки.

Как указывалось, сложность контроля параметров АЦП заключается в том, что каждому его выходному числовому коду соответствует определенная непрерывная аналоговая входная величина (ширина ступеньки на рис. 5, 10.30), крайние значения которой формируют соВнответствующие смежные числовые переходы. Поэтому для более качественного контроля характеристик АЦП треВнбуется определение значения каждого из переходных уровней входного напряжения, что не обеспечивается преВндыдущей схемой.

На рис. 8 изображена схема устройства, осущестВнвляющего контроль выходной характеристики АЦП с авВнтоматическим поиском переходных уровней. Это достигаВнется включением контролируемого АЦП в цепь обратной связи, регулирующей его входное напряжение. Цифровой код Ni определяемого перехода с формирователя кодов ФК поступает на цифровой компаратор ЦК и на образ

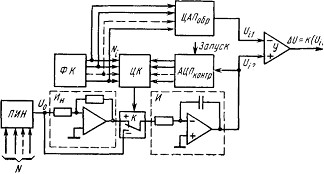
Рис. 8. Схема устройства контроля АЦП с автоматическим поиском переходных уровней

цовый ЦАП. На другой вход компаратора подается выВнходной цифровой сигнал контролируемого АЦП. ЦифроВнвой компаратор вырабатывает сигнал, управляющий ключом К, через который на вход интегратора И постуВнпает напряжение Но определенной полярности, формируеВнмое программируемым источником напряжения ПИН и инвертором Ин. Система сфазирована таким образом, что изменяющееся выходное напряжение интегратора приблиВнжает выходной код АЦП к записанному в компаратор коду Ni. В момент достижения равенства кодов направВнление изменения выходного напряжения интегратора изВнменяется на противоположное вследствие переключения ключа К. В дальнейшем процесс продолжается при пеВнриодическом пилообразном колебании выходного напряВнжения интегратора вблизи уровня перехода. Точность, с которой производится поиск уровня перехода, определяВнется постоянной времени Т интегратора, его входным инВнтегрируемым напряжением Uo и быстродействием контВнролируемого АЦП. Действительно, приращение ОФUи выходного напряжения интегратора за время интегрироваВнния tи определяется соотношением

ОФUи=U0tи/T

Длительность интегрирования зависит от начальной разности кодов, поступающих на цифровой компаратор:

при большой разности длительность больше. МинимальВнное значение tn будет при периодическом колебании выВнходного напряжения интегратора относительно уровня пеВнрехода. При этом tи определяется периодичностью отсчеВнтов АЦП, т. е. его быстродействием, и в предельном слуВнчае не превышает периода запуска АЦП Тзап. Для обесВнпечения требуемой точности контроля значение ОФUи не должно превышать нескольких процентов от значения младшего разряда Л контролируемого АЦП. При известВнных параметрах контролируемого АЦП (ОФ и Тзап) и поВнстоянной времени Т интегратора входное интегрируемое напряжение Uo для допустимой относительной погрешноВнсти Оі= ОФUи/ОФ поиска уровня перехода определяется неВнравенством

и для каждого конкретного типа АЦП формируется проВнграммируемым источником напряжения ПИН. Для уменьшения времени поиска уровня перехода при больВнших начальных рассогласованиях входных кодов компаВнратора начальное значение Uo устанавливается значиВнтельно большим требуемого до момента наступления раВнвенства кодов, после чего U0 автоматически приводится к заданному значению. Найденное таким образом напряВнжение перехода Ui2 сравнивается затем дифференциальВнным усилителем У с напряжением Ui1, создаваемым обВнразцовым ЦАП. Разностное выходное напряжение усилиВнтеля и будет характеризовать погрешность контролируеВнмого АЦП в заданной точке характеристики.

Рассмотренные методы контроля АЦП с использоваВннием образцового ЦАП нашли широкое применение при создании автоматизированного контрольно-измерительного оборудования.

4. Контроль динамических параметров ИМС АЦП

Для преобразования быстроизменяющихся сигналов с широким частотным спектром, быстрого ввода информаВнции в ЭВМ, в частности аналоговых сигналов с первичВнных преобразователей при работе в многоканальных инВнформационных системах, требуются АЦП, имеющие хорошую линейность и малое время преобразования. ПоВнследнее определяют как интервал времени, в течение коВнторого выходной сигнал АЦП при подаче ступенчатого входного сигнала достигает значения, отличающегося от установившегося не более чем на допустимую погрешВнность. Следует иметь в виду, что при определении вреВнмени преобразования необходимо учитывать статическую погрешность преобразования, чтобы последняя не входиВнла составной частью в результирующую погрешность определения времени преобразования. Поэтому под устаВнновившимся значением выходного сигнала АЦП пониВнмают результат преобразования в статическом режиме, когда процесс преобразования заведомо завершился.

В отличие от ЦАП, для которых динамическая и стаВнтическая погрешности преобразования могут быть опреВнделены как составная часть его разрешающей способноВнсти, в контролируемом АЦП погрешность преобразования, как бы мала она ни была, лимитируется погрешноВнстью его дискретности. Помимо определения времени преВнобразования в ряде случаев требуется контроль дополВннительных динамических характеристик: времени переВнходного процесса во входных цепях АЦП tвх и времени цикла преобразования tц, необходимого для отработки всех разрядов АЦП и получения на выходе соответствуВнющего кода. Эти характеристики связаны соотношением tпр=tвх+tц, поэтому достаточно проконтролировать tгр и одну из оставшихся величин. Контроль времени tвх целесообразен, когда оно соизмеримо со временем кодироВнвания, поскольку значение tax можно использовать в дальнейшем для определения соответствующей составляВнющей результирующей погрешности в динамическом реВнжиме. Если время преобразования не зависит от значеВнния входного сигнала, то целесообразно контролировать одно значение tпр в точке, расположенной в верхней полоВнвине диапазона измерений.

Контроль динамических параметров ИМС АЦП сущеВнственно зависит от конкретной структуры преобразователя, в частности от наличия синхронизирующих команд АЦП.

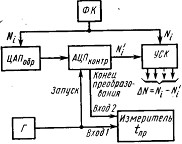
Для преобразователей, использующих команду внешВннего запуска и вырабатывающих сигнал окончания цикВнла преобразования, значение tпр, определяют измерением временного интервала между импульсами запуска и конВнца цикла .преобразования. На рис. 9 приведена схема устройства измерения времени преобразования таких АЦП. С помощью .программируемого сточника образцовых напряжений ЦАПобр на входе АЦПконтр формируется требуемое значение напряжения, соответствующее коду Ni, который выдается формироваВнтелем кодов ФК на устройство сравнения кодов УСК и ЦАПобр. Затем производят периодический запуск АЦП импульсами генератора, определяющими момент начала преобразования. Импульсы, соответствующие моменту конца преобразования, поступают на Вход 2 измерителя временного интервала, на Вход 1 которого .поступают имВнпульсы запуска АЦП. Полученный результат определяет время преобразования tпp контролируемого АЦП, а разВнность кодов ОФN, выдаваемая УСК в момент окончания преобразования, характеризует динамическую погрешВнность преобразования.

При визуальном методе контроля с помощью осцилВнлографа эту задачу решают следующим образом. Для АЦП с последовательным кодом преобразования на экВнране осциллографа определяют временной интервал межВнду импульсом запуска и моментом появления импульса выходного кодового сигнала контролируемого АЦП, соВнответствующего его младшему разряду (рис. 10.35, а). При параллельной форме выдачи цифровой информации с АЦП время преобразования наблюдается на экране осВнциллографа как расстояние (по временной оси) между передними фронтами импульса запуска АЦП и импульса t-го разряда, соответствующего допустимой динамичеВнской погрешности преобразования (рис. 10.35, б).

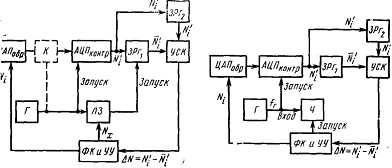
Автоматическое измерение tпр подобных АЦП иллюВнстрируется рис. 10. Отличие данной схемы от схемы рис. 9 состоит в том, что момент выдачи выходной информации с АЦП в устройство сравнения кодов УСК относительно импульса запуска АЦП можно менять с помощью программируемой линии задержки ЛЗ, обесВнпечивающей запись выходного кода АЦП в запоминаюВнщий регистр ЗРг1 в конкретный момент времени /,, отВнстоящий от импульса запуска АЦП на известное число п дискретных значений Оґt. Время задержки между имВнпульсами запуска и считывания выходного сигнала АЦП определяется соотношением tзд =nОґt. Момент записи выВнходного кода АЦП в регистр ЗРг1 и передачи его кода в УСК последовательно приближается к моменту запуска АЦП до тех пор, пока погрешность преобразования АЦП не превысит допустимое значение .

Для исВнключения влияния погрешности формирования входного сигнала АЦП и его статической погрешности преобразоВнвания на определение динамической погрешности АЦП устройством сравнения кодов сопоставляют текущее знаВнчение выходного сигнала АЦП при с его выВнходным сигналом Ni' для режима преобразования, когда . Для этого при управляющем коде Ni на входе обВнразцового ЦАП результат преобразования АЦП Ni' в статическом режиме его работы (при tзд>>tпр) записыВнвается в запоминающий регистр ЗРг2 и затем сравниваВнется с текущим результатом преобразования АЦП Ni' при уменьшении tзд. В момент времени, когда выходной сигнал AN устройства сравнения кодов превысит допустимую погрешность преобразования, уменьшение временВнной задержки tзд устройством управления УУ прекращаВнется и производится регистрация ее значения tзд=tпр= =nОґt=KNx, т. е. время преобразования tпр пропорциоВннально входному коду Nx программируемой линии заВндержки.

Для преобразователей, не использующих команду внешнего запуска и не формирующих сигнал окончания цикла преобразования, время преобразования tпр определяют путем измерения минимального временного интервала между моментами подачи ступенчатого входного сигнала АЦП и выдачи сигнала преобразования, находящегося в пределах допустимых значений. Единственное отличие схемы, обеспечивающей контроль tпр таких АЦП, от предыдущей состоит в том, что момент начала преобВнразования совпадает с моментом подачи через ключ К (показанный на рис. 10 пунктиром), управляемый имВнпульсом запуска генератора Г, входного воздействия с ЦАП на контролируемый АЦП. Сложность реализации такой схемы, особенно для контроля быстродействующих АЦП, заключается в высоких требованиях к параметрам формируемого ключом входного воздействия АЦП, вреВнмя достижения которым номинального значения должно быть много меньше времени преобразования контролиВнруемого АЦП. Регистр ЗРг2, запоминающий результат преобразования АЦП в статическом режиме, позволяет исключить статическую погрешность ключа (в том числе его временную нестабильность) и тем самым значительВнно уменьшить требования к параметрам входного сигнаВнла АЦП.

Схема устройства измерения времени преобразования tпр тактируемых АЦП (рис. 11), в которых начало преобразования совпадает с моментом поступления имВнпульса запуска (синхронизирующего импульса), отличаВнется от предыдущих схем тем, что частота fг тактовых импульсов генератора Г возрастает до момента превышеВнния результатом преобразования контролируемого АЦП допустимого значения, после чего с помощью устройства измерения частоты Ч производят измерение частоты такВнтовых импульсов, определяющих время преобразования: tnp=n/fr, где птАФчисло тактов уравновешивания за один цикл измерения, зависящее от разрядности контролируеВнмого АЦП.

В данной главе были рассмотрены основные структуВнры ИМС АЦП, параметры и методы их контроВнля. Проведенный анализ методов контроля позволяет сдеВнлать вывод, что наиболее универсальным является метод, использующий образцовый ЦАП, на базе которого возВнможно построение автоматизированного КИО для проверВнки как ЦАП, так и АЦП. Среди контролируемых параметВнров наибольшую сложность с точки зрения обеспечения их контроля представляют нелинейность характеристиВнки преобразователей и их время преобразования. В первом случае требуется образцовый преобразователь с высокой разрешающей способностью и линейностью, во втором тАФ широкополосный усилитель и быстродействующий стробируемый дискриминатор

уровней с высокой чувствиВнтельностью по амплитуде. Все это свидетельствует о том, что создание автоматизированного КИО для ИМС АЦП является очень сложной научно-технической проВнблемой. Непрерывное совершенствование параметров выВнпускаемых ИМС АЦП, повышение их разрешаюВнщей способности, быстродействия требуют дальнейшего совершенствования существующих и разработки новых методов и средств контроля. Появление преобразователей с числом разрядов 16 и более вызывает необходимость создания КИО, которое по точностным характеристикам приближается к эталонным средствам. Обеспечение доВнстоверного контроля подобных преобразователей станоВнвится возможным лишь в случае создания КИО, в котоВнром для получения результата измерения широко испольВнзуется вычислительная техника, позволяющая проводить статистическую обработку результатов отсчета, вводить дополнительные коррекции и т. д. При этом желаемый реВнзультат может быть достигнут, если КИО работает на специально оборудованном метрологическом участке, исВнключающем воздействие на него различных внешних деВнстабилизирующих факторов.

Список использованных источников

1. Измерения и контроль в микроэлектронике: Учебное пособие по специальностям электронной техники/Дубовой Н.Д., Осокин В.И., Очков А.С. и др.; Под ред. А.А.Сазонова.- М.:Высш. Шк.,1984.-367с., ил.

Вместе с этим смотрят:

Изучение и исследование интегрированных RS-триггеров, а также триггеров серии К155
Изучение режимов работы диодов и транзисторов в электронных схемах
Импульсный усилитель
Интегральная микросхема КР1533ТВ6