Математическое программирование

Общая задача линейного программирования (ЗЛП):

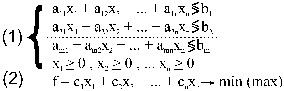
Здесь (1) называется системой ограничений , ее матрица имеет ранг r ≤ n, (2) - функцией цели (целевой функцией). Неотрицательное решение (х10, x20, .. , xn0) системы (1) называется допустимым решением (планом) ЗЛП. Допустимое решение называется оптимальным, если оно обращает целевую функцию (2) в min или max (оптимум).

Симплексная форма ЗЛП. Для решения ЗЛП симплекс - методом необходимо ее привести к определенной (симплексной) форме:

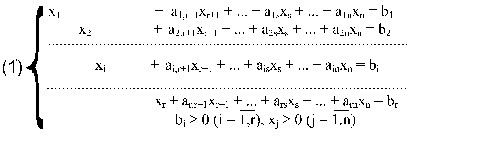(2`) f+cr+1xr+1 + .. + csxs + .. + cnxn = b0 → min

Здесь считаем r < n (система имеет бесчисленное множество решений), случай r = n неинтересен: в этом случае система имеет единственное решение и если оно допустимое, то автоматически становится оптимальным.

В системе (1`) неизвестные х1, х2, .. , хr называются базисными (каждое из них входит в одно и только одно уравнение с коэффициентом +1), остальные хr+1, .. , xn - свободными. Допустимое решение (1`) называется базисным (опорным планом), если все свободные неизвестные равны 0, а соответствующее ему значение целевой функции f(x10, .. , xr0,0, .. ,0) называется базисным.

В силу важности особенностей симплексной формы выразим их и словами:

а) система (1`) удовлетворяет условиям :

все ограничения - в виде уравнений;
все свободные члены неотрицательны, т.е. bi ≥ 0;
имеет базисные неизвестные;

б) целевая функция (2`) удовлетворяет условиям :

содержит только свободные неизвестные;
все члены перенесены влево, кроме свободного члена b0;
обязательна минимизация (случай max сводится к min по формуле max f = - min(-f)).

Матричная форма симплекс-метода. Симплексной форме ЗЛП соответствует симплекс - матрица :

1 0 .. 0 .. 0 a1,r+1 .. a1s .. a1n b1

0 1 .. 0 .. 0 a2,r+1 .. a2s .. a2n b2

.................................

0 0 .. 1 .. 0 ai,r+1 .. ais .. ain bi

.................................

0 0 .. 0 .. 1 ar,r+1 .. ars .. arn br

0 0 .. 0 .. 0 cr+1 .. cs .. cn b0

Заметим, что каждому базису (системе базисных неизвестных ) соответствует своя симплекс - матрица , базисное решение х = (b1,b2, .. ,br, 0, .. ,0) и базисное значение целевой функции f(b1,b2, .. ,br, 0, .. ,0) = b0 (см. Последний столбец !).

Критерий оптимальности плана . Если в последней (целевой) строке симплекс-матрицы все элементы неположительны, без учета последнего b0, то соответствующий этой матрице план оптимален,

т.е. сj ≤ 0 (j = r+1, n) => min f (b1, .. ,b2,0, .. ,0) = b0.

Критерий отсутствия оптимальности. Если в симплекс-матрице имеется столбец (S-й), в котором последний элемент сs > 0, a все остальные элементы неположительны, то ЗЛП не имеет оптимального плана, т.е. сs > 0, ais ≤ 0 ( i= 1,r ) => min f = -∞.

Если в симплекс-матрице не выполняются оба критерия, то в поисках оптимума надо переходить к следующей матрице с помощью некоторого элемента ais > 0 и следующих преобразований (симплексных):

все элементы i-й строки делим на элемент a+is;
все элементы S-го столбца, кроме ais=1, заменяем нулями;
все остальные элементы матрицы преобразуем по правилу прямоугольника, что схематично показано на фрагменте матрицы и дано в формулах:

akl` = akbais - ailaks = akl - ailaks;

ais ais

bk` = bkais - biaks; cl` = clais - csail

ais ais

Определение. Элемент ais+ называется разрешающим, если преобразование матрицы с его помощью обеспечивает уменьшение (невозрастание) значения, целевой функции; строка и столбец, на пересечении которых находится разрешающий элемент, также называются разрешающими.

Критерий выбора разрешающего элемента. Если элемент ais+ удовлетворяет условию

bi = min bk

ais0 aks0+

где s0 - номер выбранного разрешающего столбца, то он является разрешающим.

Алгоритм симплекс-метода (по минимизации).

систему ограничений и целевую функцию ЗЛП приводим к симплексной форме;
составим симплекс-матрицу из коэффициентов системы и целевой функции в симплексной форме;
проверка матрицы на выполнение критерия оптимальности; если он выполняется, то решение закончено;
при невыполнении критерия оптимальности проверяем выполнение критерия отсутствия оптимальности; в случае выполнения последнего решение закончено - нет оптимального плана;
в случае невыполнения обоих критериев находим разрешающий элемент для перехода к следующей матрице, для чего :

а) выбираем разрешающий столбец по наибольшему из положи тельных элементов целевой строки;

б) выбираем разрешающую строку по критерию выбора разрешающего элемента; на их пересечении находится разрешающий элемент;

c помощью разрешающего элемента и симплекс-преобразований переходим к следующей матрице;
вновь полученную симплекс-матрицу проверяем описанным выше способом (см. п. 3)

Через конечное число шагов, как правило получаем оптимальный план ЗЛП или его отсутствие

Замечания.

Если в разрешающей строке (столбце) имеется нуль, то в соответствующем ему столбце (строке) элементы остаются без изменения при симплекс-преобразованиях.
преобразования - вычисления удобно начинать с целевой строки; если при этом окажется, что выполняется критерий оптимальности, то можно ограничиться вычислением элементов последнего столбца.
при переходе от одной матрицы к другой свободные члены уравнений остаются неотрицательными; появление отрицатель

ного члена сигнализирует о допущенной ошибке в предыдущих вычислениях.

правильность полученного ответа - оптимального плана - проверяется путем подстановки значений базисных неизвестных в целевую функцию; ответы должны совпасть.

5. Геометрическая интерпретация ЗЛП и графический метод решения (при двух неизвестных)

Система ограничений ЗЛП геометрически представляет собой многоугольник или многоугольную область как пересечение полуплоскостей - геометрических образов неравенств системы. Целевая функция f = c1x1 + c2x2 геометрически изображает семейство параллельных прямых, перпендикулярных вектору n (с1,с2).

Теорема. При перемещении прямой целевой функции направлении вектора n значения целевой функции возрастают, в противоположном направлении - убывают.

На этих утверждениях основан графический метод решения ЗЛП.

Алгоритм графического метода решения ЗЛП.

В системе координат построить прямые по уравнениям, соответствующим каждому неравенству системы ограничений;
найти полуплоскости решения каждого неравенства системы (обозначить стрелками);
найти многоугольник (многоугольную область) решений системы ограничений как пересечение полуплоскостей;
построить вектор n (с1,с2) по коэффициентам целевой функции f = c1x1 + c2x2;
в семействе параллельных прямых целевой функции выделить одну, например, через начало координат;
перемещать прямую целевой функции параллельно самой себе по области решения, достигая max f при движении вектора n и min f при движении в противоположном направлении.
найти координаты точек max и min по чертежу и вычислить значения функции в этих точках (ответы).

Постановка транспортной задачи.

Приведем экономическую формулировку транспортной задачи по критерию стоимости:

Однородный груз, имеющийся в m пунктах отправления (производства) А1, А2, .., Аm соответственно в количествах а1, а2, .., аm единиц, требуется доставить в каждый из n пунктов назначения (потребления) В1, В2, .., Вn соответственно в количествах b1, b2, .., bn единиц. Стоимость перевозки (тариф) единицы продукта из Ai в Bj известна для всех маршрутов AiBj и равна Cij (i=1,m; j=1,n). Требуется составить такой план перевозок, при котором весь груз из пунктов отправления вывозиться и запросы всех пунктов потребления удовлетворяются (закрытая модель), а суммарные транспортные расходы минимальны.

Условия задачи удобно располагать в таблицу, вписывая в клетки количество перевозимого груза из Ai в Bj груза Xij > 0, а в маленькие клетки - соответствующие тарифы Cij:

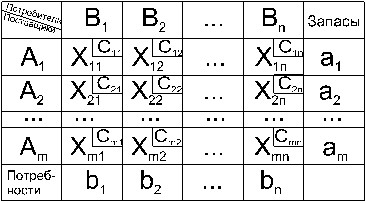
Математическая модель транспортной задачи.

Из предыдущей таблицы легко усматривается и составляется математическая модель транспортной задачи для закрытой модели

Число r = m + n - 1, равное рангу системы (1), называется рангом транспортной задачи. Если число заполненных клеток (Xij ≠ 0) в таблице равно r, то план называется невырожденным, а если это число меньше r, то план вырожденный - в этом случае в некоторые клетки вписывается столько нулей (условно заполненные клетки), чтобы общее число заполненных клеток было равно r.

Случай открытой модели Огаi ≠ Огbj легко сводится к закрытой модели путем введения фиктивного потребителя Bn+1 c потребностью bn+1=Огai-Огbj, либо - фиктивного поставщика Аm+1 c запасом am+1=Огbj-Огai ; при этом тарифы фиктивных участников принимаются равными 0.

Способы составления 1-таблицы (опорного плана).

Способ северо-западного угла (диагональный). Сущность способа заключается в том, что на каждом шаге заполняется левая верхняя клетка (северо-западная) оставшейся части таблицы, причем максимально возможным числом: либо полностью вывозиться груз из Аi, либо полностью удовлетворяется потребность Bj. Процедура продолжается до тех пор, пока на каком-то шаге не исчерпаются запасы ai и не удовлетворяются потребности bj . В заключение проверяют, что найденные компоненты плана Xij удовлетворяют горизонтальным и вертикальным уравнениям и что выполняется условие невырожденности плана.
Способ наименьшего тарифа. Сущность способа в том, что на каждом шаге заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф; в случае наличия нескольких таких равных тарифов заполняется любая из них. В остальном действуют аналогично предыдущему способу.

Метод потенциалов решения транспортной задачи.

Определение: потенциалами решения называются числа αi→Ai, βj→Bj, удовлетворяющие условию αi+βj=Cij (*) для всех заполненных клеток (i,j).

Соотношения (*) определяют систему из m+n-1 линейных уравнений с m+n неизвестными, имеющую бесчисленное множество решений; для ее определенности одному неизвестному придают любое число (обычно α1=0), тогда все остальные неизвестные определяются однозначно.

Критерий оптимальности. Если известны потенциалы решения X0 транспортной задачи и для всех незаполненных клеток выполняются условия αi+βj ≤ Ci j, то X0 является оптимальным планом транспортной задачи.

Если план не оптимален, то необходимо перейти к следующему плану (таблице) так, чтобы транспортные расходы не увеличились.

Определение: циклом пересчета таблицы называется последовательность клеток, удовлетворяющая условиям:

одна клетка пустая, все остальные занятые;
любые две соседние клетки находятся в одной строке или в одном столбце;
никакие 3 соседние клетки не могут быть в одной строке или в одном столбце .

Пустой клетке присваивают знак тАЬ + тАЭ, остальным - поочередно знаки тАЬ - тАЭ и тАЬ + тАЭ.

Для перераспределения плана перевозок с помощью цикла перерасчета сначала находят незаполненную клетку (r, s), в которой αr+βs>Crs, и строят соответствующий цикл; затем в минусовых клетках находят число X=min{Xij}. Далее составляют новую таблицу по следующему правилу:

в плюсовые клетки добавляем X;
из минусовых клеток отнимаем Х;
все остальные клетки вне цикла остаются без изменения.

Получим новую таблицу, дающее новое решение X, такое, что f(X1) ≤ f(X0); оно снова проверяется на оптимальность через конечное число шагов обязательно найдем оптимальный план транспортной задачи, ибо он всегда существует.

Алгоритм метода потенциалов.

проверяем тип модели транспортной задачи и в случае открытой модели сводим ее к закрытой;
находим опорный план перевозок путем составления 1-й таблицы одним из способов - северо-западного угла или наименьшего тарифа;
проверяем план (таблицу) на удовлетворение системе уравнений и на невыражденность; в случае вырождения плана добавляем условно заполненные клетки с помощью тАЬ 0 тАЭ;
проверяем опорный план на оптимальность, для чего:

а) составляем систему уравнений потенциалов по заполненным клеткам;

б) находим одно из ее решений при α1=0;

в) находим суммы αi+βj=C′ij (тАЬкосвенные тарифытАЭ) для всех пустых клеток;

г) сравниваем косвенные тарифы с истинными: если косвенные тарифы не превосходят соответствующих истинных(C′ij ≤ Cij) во всех пустых клетках, то план оптимален (критерий оптимальности). Решение закончено: ответ дается в виде плана перевозок последней таблицы и значения min f.

Если критерий оптимальности не выполняется, то переходим к следующему шагу.

Для перехода к следующей таблице (плану):

а) выбираем одну из пустых клеток, где косвенный тариф больше истинного (C′ij= αi+βj > Cij );

б) составляем цикл пересчета для этой клетки и расставляем знаки тАЬ + тАЭ, тАЬ - тАЭ в вершинах цикла путем их чередования, приписывая пустой клетке тАЬ + тАЭ;

в) находим число перерасчета по циклу: число X=min{Xij}, где Xij - числа в заполненных клетках со знаком тАЬ - тАЭ;

г) составляем новую таблицу, добавляя X в плюсовые клетки и отнимая X из минусовых клеток цикла

См. п. 3 и т.д.

Через конечное число шагов (циклов) обязательно приходим к ответу, ибо транспортная задача всегда имеет решение.

Вместе с этим смотрят:

Матричный анализ
Метод Гаусса
Метод Гаусса с выбором главного элемента
Метод Зойтендейка