Опыт использования ЭВМ на уроках математики

Обеспечение всеобщей компьютерной грамотности

Ядром методической системы обеспечения всеобщей компьюВнтерной грамотности является новый учебный предмет ВлОсновы информатики и вычислительной техникиВ».

Содержание курса определялось из целей и задач обеспеВнчения всеобщей компьютерной грамотности учащихся, а также с учеВнтом следующих принципиальных позиций:

на первом этапе внедрения курса информатики подавляющее большинство школ страны не располагали вычислительной техникой, поэтому первый вариант учебного пособия был ориентирован на безмашинный вариант изучения курса;

компьютерная грамотность обеспечивается изучением не одного курса информатики, а комплекса учебных предметов. ПоВнэтому при разработке содержания этого курса учитывались функВнции и вклад в компьютерную грамотность других предметов;

курс основ информатики и вычислительной техники, ставший фундаментальной компонентой общего среднего образования, разВнрабатывался как общеобразовательный и доступный для всех учащихся, т. е. он должен решать задачи не только подгоВнтовки учащихся к практической деятельности, внедрения компьютеВнров в большинство областей народного хозяйства, но и задачи умственного развития, формирования научного мировоззрения, восВнпитания учащихся и др. Кроме того, общеобразовательный харакВнтер этого учебного предмета требует доступности его содержания для всех школьников, учащихся ПТУ и техникумов;

курс информатики должен иметь межпредметный характер;

курс информатики должен сформировать у учащихся совоВнкупность знаний, умений и навыков, обеспечивающих достижение второй задачи внедрения ЭВМ в среднее образование тАФ широкое использование компьютеров в процессе изучения всех общеобразоВнвательных учебных предметов, а также и трудовое обучение;

информатика как наука является ВлмолодойВ» отраслью научного знания, поэтому имеется немало различных позиций относительно круга вопросов, составляющих ее предмет, а также удельного веса каждого из этих вопросов в содержании этой науки. Поэтому курс школьной информатики как основы данной отрасли знаний должен отражать ту инвариантную часть этой науки, которая соВндержится в определении предмета информатики, даваемого различВнными авторами;

как другой любой школьный предмет основы информатики должны не только познакомить учащихся с кругом вопросов, изуВнчаемых этой наукой, но и сформировать определенный комплекс практических умений и навыков. Обеспечить курс системой задач и упражнений, практических работ в условиях безмашинного ваВнрианта обучения было возможно, лишь сосредоточив основное вниВнмание на его содержании, на формировании алгоритмической кульВнтуры, развитии навыков программирования. Однако такое переВнраспределение удельного веса в пользу этих компонентов компьюВнтерной грамотности тАФ временная мера, отражающая специфику именно безмашинного варианта изучения курса.

Содержание курса базируется на трех фундаментальных поняВнтиях современной науки: информация тАФ алгоритм тАФ ЭВМ. Именно эта система понятий задает обязательный уровень теоретической подготовки.

В задачи нового курса входит:

овладение основными умениями алгоритмизации;

формирование представлений о возможности автоматизации выполнения алгоритма;

усиление прикладной и политехнической направленности алгоВнритмической линии, заключающееся в конкретной реализации алгоВнритмов решения задач на современных ЭВМ;

ознакомление с основами современной вычислительной техники на примере рассмотрения общих принципов работы микрокомпьютера;

формирование представления об этапах решения задачи на ЭВМ;

ознакомление с основными сферами применения вычислиВнтельной техники, ее ролью в развитии общества.

Основная позиция авторского коллектива при создании учебного пособия заключается в том, что курс основ информаВнтики и вычислительной техники есть общеобразовательный предмет. Его главная задача тАФ дать школьникам основы науки информатики, а не сделать их профессиональными программистами. Поэтому, среди фундаментальных понятий, отражающих общеобразовательВнный характер науки информатики в учебном пособии были отобраны понятия компьютерного подхода к решению задач и алгоритма.

Алгоритмический стиль мышления является характерной чертой науки информатики. Он проявляется не только как метод решения задачи, но и как последовательность методов подготовки задачи к ее решению на ЭВМ. Эту последовательность также можно расВнсматривать как своеобраз-ный алгоритм. Отдельными шагами этого алгоритма являются этапы решения задачи.

Как всегда, решение задачи начинается с ее постановки. В инВнформатике этот этап приобретает особое значение благодаря тому, что в постановке задачи участвуют реальные, а не математические объекты. Чтобы решить такую задачу, необходимо построить ее математическую модель. Об этом этапе погоВнворим подробнее. Понятие математической модели в неявном виде присутствует и в школьных курсах математики и физики, однако только в курсе информатики понятие модели формулируется в явном виде, и ставятся задачи на построение модели. ПоняВнтие модели, появившееся в курсе основ информатики,тАФ одно из самых важных ВлприобретенийВ» для средней школы. Ведь понятие модели в наши дни приобрело чрезвычайную общность и уже вышло из сферы чисто математических понятий. Оно широко используется в химии, биологии, социологии и т. д. В мировоззренческом плане очень важно научить школьников различать факты, относящиеся к реальному миру и к его модели.

Алгоритмический язык предназначен для единообразной записи и исполнения алгоритмов. Методическая целесообразность его введеВнния в курс заключается в следующем. С одной стороны, алгоВнритмический язык близок к естественному языку. Командами алгоВнритмического языка могут быть любые предложения русского языВнка в повелительном наклонении. С другой стороны, правила алгоВнритмического языка составлены таким образом, чтобы сделать его похожим на реальный язык программирования, который учащимВнся придется изучать в дальнейшем. Таким образом, с первых шагов изучения информатики учащиеся получают теоретические представВнления о конструкциях, которые лежат в основе практически всех современных языков программирования.

Изучение алгоритмического языка тАФ одна из важнейших заВндач курса информатики. Алгоритмический язык выполняет две осВнновные функции. Во-первых, его применение позволяет стандарВнтизировать, придать единую форму всем рассматриваемым в курсе алгоритмам, что важно для формирования алгоритмической культуВнры школьников. Во-вторых, изучение алгоритмического языка явВнляется пропедевтикой изучения языка программирования. МетодиВнческая ценность алгоритмического языка объясняется еще и тем, что в условиях, когда многие школьники не будут располагать ЭВМ, алгоритмический язык является наиболее подходящим языком, ориентированным для исполнения их человеком.

Изучение языка программирования в курсе основ информатики преследует две цели. Во-первых, это иллюстративная цель тАФ показать школьникам, как конструкции алгоритмического языка могут быть выражены средствами языка программирования, предназначенного для ЭВМ. Во-вторых, прикладная цель тАФ дать учащимся возможность исполнить на ЭВМ те несложные алгоритмы, которые они освоили или разработали сами при изуВнчении основ алгоритмизации.

Одна из важнейших задач курса информатики тАФ познакомить учащихся с основными областями применения ЭВМ, сформировать представления о вычислительной технике как средстве повышения эффективности деятельности человека. Конечно, эта задача должна пронизывать все содержание курса, каждый урок по этому предмету. Однако при отсутствии в школе кабинетов вычислительВнной техники особая роль здесь принадлежит экскурсии в ВычислиВнтельный центр.

С точки зрения содержания курса произойдет значительная переориентация на формирование умений использования ЭВМ в разВнличных областях деятельности человека, умений применять готоВнвое прикладное программное обеспечение. С точки зрения метоВндики обучения произойдет коренная перестройка организации учебного процесса на основе систематической работы школьников с компьютером как средством обучения. Это сделает усвоение учебного материала более доступным, значительно усилит познаВнвательные возможности школьников, существенно активизирует их самостоятельную учебную деятельность.

Новая программа и методика курса позволит в более полной мере решить задачу достижения компьютерной грамотности, как она поставлена в ВлОсновных направлениях реформы общеобразоваВнтельной и профессиональной школыВ» тАФ вооружить учащихся знаВнниями и навыками использования современной вычислительной техВнники.

Школьники должны освоить системы обработки текстовой инВнформации, получить навыки работы с текстами на ЭВМ, хранения и вывода текстов на печать, познакомиться с машинной графикой. Большое прикладное значение будет иметь формирование в курсе умений работать с базами данных, с электронными таблицами, а также формирование навыков применения пакетов прикладных программ для решения разного рода задач. Наконец, учащиеся познакомятся с такими важнейшими сферами использования вычиВнслительной техники в производстве, как станки с программным управлением, машины со встроенными микропроцессорами, автоВнматизированные рабочие места. Школьники получат представление об АСУ и автоматизации проектирования, применения ЭВМ в науке, медицине, образовании. Следует подчеркнуть, что это знакомство произойдет не только на страницах учебника, но прежВнде всего в процессе работы пусть с простейшими учебными, но реальными системами, реализованными на школьной ЭВМ.

Информатика на своих уроках объединит в ЭВМ предмет и средство обучения. Это окажет значительное влияние на органиВнзацию учебного процесса. Специфика урока информатики проявитВнся прежде всего в существенном объеме практических работ с использованием ЭВМ, при котором Влконтактное времяВ» работы с ЭВМ составляет не менее половины урока. В курсе предусматриВнваются три вида организованного использования кабинета вычисВнлительной техники на уроках информатики: демонстрация, лабоВнраторная работа (фронтальная) и практикум. Эти виды практичеВнских работ различаются по длительности и по соотношению роли преподавателя и учащихся.

Демонстрация: работу на ЭВМ ведет учитель; учащиеся либо наблюдают за его действиями через демонстрационный экран, либо воспроизводят эти действия на своих рабочих местах. ЛабоВнраторная работа (фронтальная): сравнительно короткий (3тАФ15мин) период самостоятельной, но синхронной работы учащихся с учебВнным программным средством, направленной либо на его освоение, либо на закрепление материала, объясненного учителем, либо на проверку усвоения полученного знания или операционного навыка. Роль учителя во время фронтальной лабораторной работы тАФ обеспечение синхронности действий учащихся и оказание экстренной помощи по инициативе учеников. Практикум: выполнение протяженВнной самостоятельной работы с компьютером в пределах одного-двух уроков по индивидуальному заданию; работа требует синтеза знаний и умений по целому разделу курса. Учитель главным образом обеспечивает индивидуальный контроль за работой учаВнщихся.

Формирование навыков работы с компьютером, освоение приВнкладного программного обеспечения в курсе информатики позвоВнлит реализовать вторую важнейшую задачу внедрения ЭВМ в школу тАФ обеспечить широкое использование компьютеров в процессе изучения всех общеобразовательных учебных предметов, а также в трудовом обучении.

При обучении математике могут найти применение, прежде всего следующие возможности современных компьютеров.

1. Быстрота и надежность обработки информации любого вида. Отметим, что для обработки числовой информации можно испольВнзовать не только микроЭВМ, но и калькулятор.

2. Представление информации в графической форме. По своим графическим (демонстрационным) возможностям микроЭВМ пракВнтически не уступают даже цветному телевидению, но позволяют активно влиять на ход демонстраций, что значительно повышает их методическую ценность.

3. Хранение и быстрая выдача больших объемов информации. Например, все используемые в курсе математики таблицы могут храниться в памяти компьютера. Требуемая информация выдается на экран после одного-двух нажатий клавиш.

Возможности применения микроЭВМ на уроках зависят от проВнграммного обеспечения машин. Все используемые на занятиях проВнграммы можно условно разделить на обучающие и учебные. ОбуВнчающие программы создаются для того, чтобы заменить учителя в некоторых видах его деятельности (при объяснении нового материаВнла, закреплении пройденного, проверке знаний и т. п.).

Цель учебных программ тАФ помочь ученику в его познавательВнной деятельности, работе на уроке. Использование учебных проВнграмм осуществляется при участии и под руководством учителя. С помощью учебных программ можно выполнить разнообразные вычислительные операции, анализировать функции, строить и исслеВндовать математические модели различных процессов и явлений, исВнпользовать графику машины для повышения наглядности изучаемоВнго материала.

Использование пакетов прикладных учебных программ, готоВнвого программного обеспечения является одной из самых важных компонентов формирования компьютерной грамотности. При этом значительно расширяются межпредметные связи между многими учебными дисциплинами, особенно между математикой и информаВнтикой. Вычислительная техника, проникая в школьную математиВнку, может оказать большое влияние на ее содержание и структуру и, кроме того, привести к нетрадиционным формам обучения.

Элементы информатики на уроках геометрии

С целью пропедевтики основных понятий информатики была предпринята попытка включения элементов информатики в курс геометрии VI класса при решении задач на построение. АлгоритмиВнческий характер таких задач очевиден. Поэтому была сделана попытка создания алгоритмического языка для описания процесса геометрических построений.

Система указаний для построения на плоскости. Рассмотрим алгоритмы решения задач на построение при помощи циркуля и линейки. В состав таких алгоритмов входят известные школьникам указания (предписания) выполнить определенные действия. КонечВнный, используемый нами набор таких указаний будем называть системой указаний.

Приведем примеры наиболее типичных указаний нашей системы.

Провести прямую через точки А и В. Обозначить постВнроенную прямую именем а: а = пр (А, В).

Провести произвольную прямую а: а = пр (+, +).

Провести прямую через точку А: а = пр (А, +).

Провести окружность с центром в точке А и радиусом с. Обозначить построенную окружность именем 01:01=окр (А, с).

Провести окружность 01 произвольного радиуса с центром в точке А: 01=окр (А, +).

Выбрать произвольную точку на плоскости (π). Обозначить выбВнранную точку именем В: В =(+) или В=τ(π).

Выбрать произвольную точку В на прямой а: В=τ(а).

Обозначить именем тИЖl треугольник с вершинами А,В,С: тИЖ1 =тИЖАВС.

Провести полупрямую а1 с началом в точке А и проходящую через точку В: а1 =ппр (А, В).

Провести произвольную полупрямую а1 с началом в точке А:

а1=ппр (А, +).

Обозначить именем ∠A угол с вершиной в точке А и сто-- ронами, проходящими соответственно через точки С и D: ∠A= ∠C,А,D.

Запятые в обозначении угла необязательны.

Обозначить именами А и В соответствующие точки переВнсечения прямой а с окружностью О1: {А, В}=атИйО1. Обозначить именем π1 полуплоскость с границей, содерВнжащей прямую или полупрямую а1, и содержащую точку А вне границы: π1=ппл (а1, А).

В соответствии с приведенными примерами будем считать, что построения производятся в плоскости π. Рассматриваемые в алгоВнритмах полуплоскости будем обозначать буквой π вместе со следующим за ним натуральным числом. Точки будем обозначать проВнписными буквами русского или латинского алфавита, прямые или полупрямые тАФ строчными буквами. После буквы в обозначении точВнки, прямой или полупрямой допускается запись натурального числа, часто просто цифры. Обозначение окружности будет начиВннаться с буквы О, обозначение треугольника тАФ со знака тИЖ, обознаВнчение углатАФсо знака ∠В обозначении окружности, треугольВнника или угла вслед за первым символом также допускаетВнся запись последовательности цифр.

Строго говоря, отмеченные выше договоренности не являются принципиальными. Все элементы построения можно обозначать с помощью имен, состоящих из произвольной последовательности букв и цифр.

Наряду с указанными выше обозначениями, рассматривая ноВнвые элементы построения, вместе с введением новых указаний будем использовать новые обозначения, а также математические обозначения, понятные школьникам.

В записи алгоритмов также используются слова, смысл и знаВнчение которых являются постоянными в записи любых алгоритмов. Такие слова всегда записываются одинаково, обычно сокращенно и подчеркиваются.

При разработке алгоритмов на построение приведенные примеВнры указаний будем использовать в качестве образца для записи указаний.

Как видно из приведенных примеров, если в указании алгоВнритма вместо какого-нибудь параметра стоит знак Вл+В» то данВнный параметр при выполнении алгоритма выбирается произвольно. При произвольном выборе параметров предполагается выбор параВнметров, отличных от ранее используемых в алгоритме.

Указания алгоритмов будем нумеровать последовательными наВнтуральными числами. Между указанием и его номером будем стаВнвить точку.

Простейшие задачи на построение

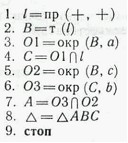
Задание 1. Построить треугольник с заданными сторонами. Предполагается, что величины сторон треугольника соответственно равны а, b, с.

Алгоритм 1.

Поясним каждое из приведенных указаний алгоритма.

1. Провести произвольную прямую l на плоскости.

2. Выбрать произвольную точку В на прямой l.

3. Провести окружность 01 с центром в точке В и радиусом а.

4. Обозначить именем С одну из точек пересечения окружВнности 01 и прямой l.

5. Провести окружность 02 с центром в точке В и радиуВнсом с.

6. Провести окружность 03 с центром в точке С и радиуВнсом b.

7. Обозначить именем А одну из точек пересечения окружВнностей 02 и 03.

8. Треугольник тИЖ с вершинами в точках Л, В, С искомый.

9. Закончить действия.

Задание 2. Отложить от данной полупрямой l1 с началом в точке О в данную полуплоскость π1 угол, равный данному угВнлу А.

Предполагается по условию задачи, что угол А задан вершиной А и двумя лучами b и с, имеющими общую вершину A.

Алгоритм 2.

Здесь указание 4 означает: провести окружность с центром в точке О и радиусом |АВ| равным расстоянию между точками A и В. Указание 6 аналогично указанию 4. Указание 7 ознаВнчает: обозначить точки пересечения окружностей 02 и 03 именами С1 и С2. Порядок обозначения произвольный.

При выполнении указания 8 проверяется принадлежность точки С1 полуплоскости π1. Если точка С1 принадлежит полуплоскости л1, то под углом О будем понимать ∠B1, О, С1 с вершиной в точке О и лучами, проходящими через точки В1 и С1. Если точка С1 не принадлежит полуплоскости π1, то под углом О будем понимать ∠B1, О, С2 с вершиной в точке О и сторонами, прохоВндящими через точки В1 и С2.

Задание 3. Построить биссектрису данного угла A, обраВнзованного лучами b и с.

Алгоритм 3. 1. 01=окр (Л, +)

2. В=O1тИйb

3. С=01тИйс

В приведенном алгоритме указание 6 означает: обозначить точку пересечения окружностей 02 и 03 именем D. Так как одВнной из точек пересечения окружностей 02 и 03 является точка A, то точка D может быть построена однозначно. Указание 7 ознаВнчает: построить полупрямую d с началом в точке А и проходящую через точку D.

Задание 4. Разделить отрезок АВ пополам.

Алгоритм 4. 1. 01=окр (A, |АВ|)

2. 02=окр (B, |AВ|)

3. {С1.С2}=01тИй02

4. l1=пр (Cl. C2)

5. M=l1тИйAВ

6. стоп

Указание 5 означает: построить точку пересечения прямой l1 и отрезка АВ.

Задание 5. Через данную точку О провести прямую l, перВнпендикулярную данной прямой а.

Алгоритм 5. 1. если О∉а то идти к 4

2. 01=окр (О, +)

3. идти к 6

4. В=τ (а)

5. 01=окр (0,2|OB|)

6. {A, С} =01тИйа

7. 02=окр (A, |AС|)

8. 03=окр (С, |AС|)

9. {D,K}=02тИй03

10. l=пр (D,K)

11. стоп

Указание 5 здесь означает: построить окружность 01 с центВнром в точке О и радиусом, равным удвоенному расстоянию между точками О и В.

Использование алгоритмов

Приведенные выше алгоритмы мы будем считать основными простейшими алгоритмами для решения задач на построение при помощи циркуля и линейки. Эти алгоритмы можно использовать для решения других задач на построение.

Для удобства обращения к алгоритмам каждому алгоритму буВндем давать название (имя) и указывать исходные данные для алВнгоритма (аргументы), а также результаты его выполнения.

Удобно, указывая аргументы и результаты алгоритма (параВнметры), одновременно указывать их тип: рацтАФрациональное чисВнло, целтАФцелое число, пртАФпрямая, ппртАФполупрямая, т тАФ точВнка, окртАФокружность, тртАФтреугольник, угтАФугол, пплтАФполуВнплоскость и т. д.

Название алгоритма, указание его параметров и их типов буВндем записывать в виде заголовка алгоритма перед первым его указанием. В качестве образца заголовка алгоритма приведем загоВнловок для алгоритма 1:

алг трг (рац а, b, с; тр тИЖ)

арг а, b, с

рез тИЖ

Имя алгоритма будем помещать в первой строчке заголовка после служебного слова алгтАФ Имя алгоритма 1 состоит из трех букв тАФ трг. После имени алгоритма в скобках указываются типы параметров алгоритма. Параметры одного типа разделяются запяВнтыми. Различные типы параметров разделяются точкой с запятой. Во второй строчке после служебного слова арг через запятую перечисляются аргументы алгоритма, в третьей строчке после слуВнжебного слова рез перечисляются результаты алгоритма.

После заголовка алгоритма будем записывать служебное слоВнво нач, после которого помещаются указания алгоритма. После последнего указания алгоритма будем записывать служебное слово кон.

Рассмотренным выше алгоритмам 2, 3, 4, 5 дадим соответстВнвенно имена: уг, бис, дел, пер.

При использовании известного алгоритма в решении задач достаточно в качестве отдельного указания записать обращение к алгоритму, состоящее из названия алгоритма и списка его паВнраметров, причем тип параметров в обращении не указывается.

Параметры, являющиеся аргументами, должны быть определены к моменту выполнения алгоритма, т. е. заданы по условию или предварительно построены (числовые вычислены).

Рассмотрим следующий пример:

Задание 6. Построить треугольник с заданными сторонами а, b, с, если а =2, b=3, с =4.

Для выполнения задания будем использовать алгоритм трг, в таком случае требуемый алгоритм может иметь следующий вид:

Алгоритм 6. ал г тр1 (рац а, b, с; тр тИЖ)

арг а, b, с

рез тИЖ

нач

1. а=2

2. b=3

3. с=4

4. трг (а, b, с, тИЖ)

5. стоп

6.кон

Первые три указания задают аргументам алгоритма трг числоВнвые значения. Указание 4 алгоритма тр1 требует применения алВнгоритма трг, который по заданным значениям длин сторон указыВнвает способ построения искомого треугольника.

Указания 1тАФ3 последнего алгоритма можно опустить, в этом случае искомый алгоритм будет иметь следующие указания:

1. трг (2, 3, 4, тИЖ)

2. стоп

Алгоритм-функция

Рассмотрим другую форму записи обращения к алгоритму. РасВнсматриваемое выше указание для построения треугольника по трем заданным сторонам трг (2, 3, 4, тИЖ) можно записать следующим образом: тИЖ=трг (2, 3, 4). Указания такого вида будем называть указаниями, имеющими форму функции.

Всякое обращение к известным алгоритмам можно записать в виде указания, имеющего форму функции. В свою очередь всякое укаВнзание на построение можно рассматривать как использование алгоВнритма, обращение к которому имеет форму функции.

Так, например, указание 01=окр (А, р) можно рассматривать как обращение к алгоритму с именем окр и параметрами A и р, являющимися аргументами алгоритма. Результат поВнстроения по данному алгоритму обозначается именем 01.

Такой алгоритм может состоять, например, из следующих укаВнзаний:

1. Сделать раствор циркуля равным р.

2. Поставить одну ножку циркуля в точку А.

3. Второй ножкой циркуля описать окружность.

4. Закончить действия.

Для указаний приведенного алгоритма можно также ввести сокращения и обозначения, удобные для записи, однако это делать необязательно, так как на практике такого рода указаниями обычно не пользуются.

Методические указания

Для изучения темы ВлГеометрические построенияВ» в VI классе средней общеобразовательной школы отводится 14 ч.

На первом уроке вводятся определения окружности, центра, радиуса, хорды окружности, диаметра. Эти понятия являются уже знакомыми для учащихся. Представляется целесообразным на этом же уроке рассмотреть простейшие указания для построения алгоВнритмов: проведение окружностей, прямых, выбор точки из множеВнства. После рассмотрения простейших указаний необходимо перейти к рассмотрению простейших алгоритмов.

Учащимся рекомендуется рассмотреть простейшие алгоритмы следующего вида:

1. Построить окружность с центром в точке О и радиусом 3 см.

2. Отложить на построенной окружности точку А и построить

отрезок О А.

3. Отметить на окружности две точки М и N. Провести хорду, их соединяющую.

4. Построить общую секущую к двум окружностям.

После выполнения каждого пункта учащиеся показывают свои записи и учитель вносит необходимые пояснения и коррективы.

На этом же уроке или в качестве домашнего задания рекоменВндуется рассмотреть алгоритмы построения к задачам 5 и 6.

На втором и третьем уроках рассматриваются понятия касаВнтельной к окружности, взаимное расположение двух окружностей, теоремы о центрах вписанной и описанной окружностей.

На этих уроках целесообразно рассмотреть указания алгоритВнмов, содержащие условные указания и указания перехода. РекоВнмендуется также использовать задания вида:

1. Провести диаметр окружности.

2. Проверить, является ли прямая касательной к окружности.

На четвертом и пятом уроках следует рассмотреть указания алгоритмов, содержащие понятия полупрямой, полуплоскости, угла, треугольника. Здесь решаются задачи, связанные с построением угла, равного данному, а также треугольника по трем заданным элементам.

На шестом, седьмом и восьмом занятиях рассматриваются вопВнросы: построение биссектрисы угла, деление отрезка пополам и построение перпендикулярной прямой.

При проведении этих занятий целесообразно рассмотреть алгоритм построения прямой, параллельной данной и проходящей чеВнрез данную точку, алгоритм построения прямой, касающейся окружВнности и проходящей через данную точку, и другие алгоритмы подобВнного типа, обращения к которым в дальнейшем можно использоВнвать как элементарные указания.

При разработке алгоритма построения прямой, параллельной данной прямой а и проходящей через данную точку А, мы исВнпользуем обращение к алгоритму 5 (построение прямой, проВнходящей через данную точку, перпендикулярно данной прямой).

Алгоритм 7. алг пар (т А, пр a, l)

арг А, а

рез l

нач пр b

1. b=пер (А, а)

2. l=пер (А, b)

3. стоп

кон

В приведенном алгоритме использовалась прямая b, которая не является параметром алгоритма. Указание типа для имени

b записано перед первым указанием алгоритма, после служебноВнго слова нач.

В дальнейшем для построения прямой l, параллельной данВнной прямой а и проходящей через данную точку А, можно исВнпользовать обращение к алгоритму 7: l=пар (А, а).

Для проведения произвольной прямой, параллельной данной прямой а, можно использовать указание: l=пар (+,о).

Приведенные указания для использования алгоритма пар можно считать элементарными и не разбивать их на более мелкие указаВнния.

Аналогично можно рассмотреть алгоритмы построения касательВнных к окружности, проходящих через данную точку.

Занятия 9тАФ14 посвящаются вопросам: геометрическое место точек, метод геометрических мест, углы, вписанные в окружность. На этих занятиях предполагается свободное использование элеменВнтов изученной учебной графической системы при рассмотрении алгоВнритмов на построение.

В целом при изучении данной темы учащиеся должны усвоить основные элементарные указания алгоритмов построения на плосВнкости, правила и особенности их использования. При этом должна ставиться цель пропедевтики курса информатики, приобретения и развития алгоритмических навыков. У учащихся должен вырабатыВнваться взгляд на алгоритмический язык как на совокупность средств и правил записи алгоритмов.

Межпредметные связи курсов Влосновы информатики и вычислительной техникиВ» и ВлМатематикаВ» при выборе задач для практики по программированию.

Можно выделить три основных этапа практики:

выбор темы задачи и составление алгоритма ее решения, написание, отладка и тестирование программы, оформление и защита отчета по проделанной работе. Мы рассмотрим здесь первый этап работы.

1. Прикладная направленность. Тема работы должна отражать реальную ситуацию, возникающую в научно-технической практике применения ЭВМ. Разумеется, уровень сложности при этом должен соответствовать возможностям школьника.

2. Математическое моделирование. Работа должна содержать составление математической модели изучаемого явления, включая такие вопросы, как сравнение различных моделей и выбор более эффективной с учетом использования компьютера.

3. Использование межпредметных связей. Работа должна опиВнраться на знания и умения, полученные школьниками на других уроках как физико-математического, так и естественного, а возВнможно, и гуманитарного цикла.

Темы работ по программированию разбиваются на три группы:

системные задачи; задачи вычислительной математики; информаВнционные, или нечисленные, задачи (разумеется, некоторые задачи находятся Влна стыкеВ»).

Системные задачи, требующие глубокого знания работы ЭВМ, обычно привлекают немногих сильных учеников. Желательно предоВнставлять им возможность индивидуальной работы

Вторую группу составляют задачи вычислительной математики. В курсах математики и программирования учащиеся знакомятся с основными методами приближенного решения уравнений, решеВнния систем линейных уравнений, с методами интерполяций и экстраполяции, с методами численного интегрирования. Это позвоВнляет предложить школьникам большой набор заданий. Однако при этом возникают затруднения методического плана.

Численный метод представляет собой полностью описанный алгоритм, и изучение его сопровождается составлением и подВнробным разбором схемы алгоритма и программы, а часто и отладкой этой программы в качестве практического задания. Поэтому задаВнние типа ВлСоставьте программу решения данного уравнения меВнтодом хордВ» ко времени прохождения практики является слишком простым и, главное, не требует самостоятельной творческой работы учащегося. Кроме того, курс вычислительной математики в школе в силу нехватки учебного времени и отсутствия развитого математического аппарата носит неполный характер и, как правило, оставляет в стороне вопросы сходимости, точности и т. п. Это моВнжет привести к неожиданным сложностям при решении практиВнческих задач. Отметим также, что если в курсе вычислительной математики изучается большое количество приближенных методов, то в школьной практике в отличие от научной применяются в основВнном точные аналитические методы, что достигается искусственным сужением класса рассматриваемых функций и подбором коэффиВнциентов. Практически все сводится к приближенному подсчету значения выражений в задачах по физике и химии.

Чтобы избежать этих трудностей, целесообразно предлагать учащимся исследовать реальные физические, химические и другие подобные ситуации, самостоятельно продумать математическую модель явления, приводящую к уравнению или системе уравнений. Эти уравнения решаются в дальнейшем путем применения численВнного метода с использованием стандартной подпрограммы, составВнленной на соответствующем уроке вычислительной математики. Желательно, чтобы уравнения, описывающие рассматриваемые явления, не решались аналитически или их решение было чересчур сложным тАФ этим наглядно демонстрируется эффективность примеВннения приближенных методов.

Большинство учащихся обычно выбирают информационные заВндачи. Как пишет известный американский специалист по системВнному программированию Д. Кнут, Влчисла в таких задачах встреВнчаются по чистой случайности, и при решении этих задач испольВнзуется способность вычислительной машины принимать решения, а не ее умение производить арифметические действияВ». Эти заВндачи позволяют охватить практически все сферы интересов учаВнщихся: математику, физику, химию, биологию, игры и многое другое. Заложенные в них математические модели и алгоритмы допускают простые и наглядные формулировки, опирающиеся на основные понятия соответствующих предметов: ВлмногочленыВ»,

Влструктуры органических молекулВ», Влэлектрические цепиВ» и т. п. При этом информационные задачи отличаются высоким уровнем логической сложности и дают возможность познакомить школьВнников с практическим использованием основных информационных структур и алгоритмов, составляющих современное нечисленное программирование.

Кроме того, информационные задачи легко поддаются метоВндической обработке тАФ небольшие изменения в формулировке задаВнния позволяют варьировать уровень трудности, с тем чтобы он соответствовал возможностям конкретного школьника.

Мы остановимся на следующих темах, отражающих межпредметные связи между курсом ОИВТ и математическими курсами:

1. Целые и рациональные алгебраические выражения.

2. Делимость чисел.

3. Разложение на множители многочленов с рациональными коэффициентами.

4. Комбинаторика.

5. Выпуклые фигуры.

Целые и рациональные алгебраические выражения.

МногоВнчлены от одного переменного образуют кольцо. Предлагается соВнставить комплекс программ, реализующих в нем операции слоВнжения, вычитания, умножения и деления с остатком.

Многочлены степени N естественно представлять в виде одноВнмерных массивов размерности (0:N), т. е. нумеруя их коэффициенты:

а(0), а(1), .., а (N). Условимся, что нулевой элемент массива соВндержит старший коэффициент многочлена, например, многочлен x3+3x+2 представляется массивом (1, 0, 3, 2).

Программы сложения и вычитания многочленов сводятся к поВнэлементным операциям над массивами, при этом нужно корректно обработать случай, когда степень одного многочлена больше стеВнпени другого.

Программа умножения работает методом накопления значений коэффициентов. На этом простом примере мы поясним способ заВнписи алгоритма, который будет использован ниже. Каждый алгоВнритм имеет название (ВлПроизведениеВ»), его шаги обозначаются первыми буквами названия и пронумерованы (Пр1 тАФПр4). Шаги содержат сравнительно крупные действия, соответствующие одному-двум операторам развитого языка уровня Алгола-68 или ПЛ/1. В других языках программирование одного шага может потреВнбовать группы операторов. Комментарии к алгоритму заключены в круглые скобки.

ПРОИЗВЕДЕНИЕ.

Пр1. ПРОИЗВ ←0 (присвоить элементам ПРОИЗВ значение 0)

Пр2. для всех i от 0 до М выполнить Пр3 тАФ Пр4.

Пр3. для всех j от 0 до N выполнить Пр4.

Пр4. ПРОИЗВ (M+N-i-j) ←ПРОИЗВ (M+N-i-j)+A (i)×B (j). Здесь A(0:M) и B(0:N)тАФперемножаемые многоВнчлены, ПРОИЗВ (0:M+N)тАФих произведение.

Более сложной является программа деления многочленов с остатком ВлуголкомВ». В ней используются четыре массива: ДЕЛМ (О :М)тАФ делимое, ДЕЛТ (0: N) тАФ делитель, ЧАСТН (0: M)тАФчастВнное и ОСТ (O:M) тАФ остаток. Поскольку любая программа не должна менять входную информацию, массивы ДЕЛМ и ДЕЛТ должны оставаться неизменными, а для промежуточных вычислений исВнпользуется массив OCT. Поэтому его размерность определена (0:M), хотя окончательно размерность остатка меньше размерности делителя. Если первые элементы массива тАФ нули, то степень соВнответствующего многочлена меньше размерности массива. ОпреВнделим функцию СТЕПЕНЬ (A), аргументом которой является масВнсив, а значением тАФ истинная степень многочлена, определяемого этим массивом. Она равна разности между числом элементов в массиве и номером первого ненулевого элемента. Алгоритм подВнсчета значения СТЕПЕНЬ тривиален.

ДЕЛЕНИЕ.

Д1. СТЕПМ ←СТЕПЕНЬ (ДЕЛМ), СТЕПN ←СТЕПЕНЬ (ДЕЛТ), ОСТ ←ДЕЛМ

Д2. для всех i от 0 до СТЕПM тАФ СТЕПN выполнить Д3 тАФ Д4

ДЗ. ЧАСТН (i) ←ДЕЛМ (СТЕПМ-i) /ДЕЛТ (N тАФ СТЕПN)

(вычисляется коэффициент частного при члене степени СТЕПM тАФ CTEПN - i)

Д4. для всех i от 0 до СТЕПN выполнить ОСТ (i+j)-OCT (i+/)- ЧАСТН (i) Х ДЕЛТ (/)

Д5. СТЕПОСТ ←СТЕПЕНЬ (ОСТ), СТЕПЧАСТН ←СТЕВнПЕНЬ (ЧАСТН) (СТЕПОСТ содержит степень остатка, ОСТ тАФ осВнтаток, СТЕПЧАСТН тАФ степень частного, ЧАСТН тАФ частное)

Задачу можно обобщить на случай рациональных алгебраиВнческих выражений от одного переменного. Алгебраическая дробь задается упорядоченной парой многочленов, и правила действий с дробями позволяют свести алгебраические действия над ними к действиям над многочленами. Соответствующие простые программы используют подпрограммы, составленные по вышеописанным алВнгоритмам. Обычно накладывается дополнительное условие, что дробь должна быть приведенной (т. е. числитель и знаменатель не должны иметь нетривиальных общих делителей), а старший коэффициент знаменателя равен 1. Разберем алгоритм приведеВнния дроби к каноническому виду. Для этого требуется использоВнвать алгоритм Евклида нахождения НОД многочленов.

ПРИВЕДЕНИЕ.

П1. QR←P, RR←Q (Q и РтАФисходные массивы, RR, QR и PRтАФрабочие массивы, используемые при вычислениях).

П2. пока RR отлично от 0 (т. е. хотя бы один элемент не раВнвен 0) выполнять ПЗ тАФ П4, иначе перейти к П5 (при этом PR соВндержит НОД Р и Q).

ПЗ. PR←QR, QR←RR.

П4. Разделить с остатком (применить ДЕЛЕНИЕ) PR на QR. Остаток поместить в RR.

П5 (разделить числитель на НОД). Разделить Р на PR, частное поместить в RR (остаток равен 0).

П6 (разделить знаменатель на НОД). Разделить Q на PR, частВнное поместить в QR (остаток равен 0).

П7. Разделить поэлементно RR и QR на первый ненулевой элемент QR (для его определения можно воспользоваться функВнцией СТЕПЕНЬ) и закончить (RR и QR содержат числитель и знаменатель дроби).

Отметим, что время работы можно сократить, убрав пересылВнки в П3. Правда, при этом увеличивается число шагов

2. Делимость чисел. Приведем пример межпредметных связей, когда математические формулы и теоремы используются для оценВнки алгоритма. Мы разберем задачу, связанную с теоремой Лагранжа. Алгоритм ее решения несложен, но дает возможность познаВнкомить школьников с проблемами анализа алгоритмов. Эти пробВнлемы наряду с тестированием незаслуженно обходятся не только в школьных, но и в вузовских курсах программирования.

Теорема Лагранжа утверждает, что каждое натуральное число может быть представлено в виде суммы четырех квадратов целых чисел. Она доказывается конструктивно, т. е. дается алгоритм поВнстроения такого разбиения для любого числа.

Доказательство опирается на понятие вычетов по простому модулю и может быть изучено сильным учеником на факультативных занятиях или по книге. Будем рассматривать только упорядоченные по убыванию разВнложения, тогда при N =i2 + j2 + k2 + l2 выполняется i≥ j≥ k≥ l. Тогда верно i2≤ N и i2 ≥ N/4, т. е. i принадлежит отрезку [/2, ] . Поскольку j, k и l не превышает i, общее число комВнбинаций можно оценить сверху Точную оценку дает формула

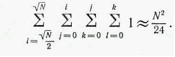
Приведем теперь алгоритм, позволяющий получить все упоряВндоченные разложения данного числа.

КВАДРАТЫ.

К1. для всех i от до /2 выполнить К2тАФК8.

К2. S1 ←i2. Если N=S1, то вывести (i).

КЗ. для j от i до 0 выполнить К4тАФК8.

К4. S2←S1+j2, Если N=S2, то вывести (i, j).

К5. для k от j до 0 выполнить КбтАФК8.

К6. S3←S2+k2, Если N =S3, то вывести (i, j, k).

К7. для l от k до 0 выполнить К8.

К8. Если N=S3+l2 то вывести (i, j, k, 1} и перейти к К5 со следующим значением k.

В этом алгоритме i, j, k и I пробегают целые значения в соотВнветствующих интервалах. S1, S2, S3 введены для сокращения объема вычислений. Выполнение шага К8 можно прекращать при нахождении первого значения, удовлетворяющего условию, поВнскольку не может быть двух разложений, отличающихся только последним числом. Небольшая модификация алгоритма позволяВнет организовать работу до нахождения первого разложения. Эта программа может быть использована для численного решения многих статистических задач: распределение чисел, представВнляемых в виде суммы 1, 2, 3, 4 квадратов, как функция N, число различных представлений в требуемом виде, а также проверить приведенную нами оценку числа комбинаций.

3. Решение алгебраических уравнений с рациональными коэфВнфициентами. Обычно в школьной практике уравнения вида аоxn+a1 xn-1+ +тАж+an=0 имеют рациональные коэффициенты. В этом случае имеется эффективный алгоритм нахождения всех рациоВннальных корней. Прежде чем разбирать его, отметим, что умноВнжение на НОК знаменателей коэффициентов позволяет сделать их целыми числами. Если старший коэффициент отличен от едиВнницы, то умножим уравнение на a0n-1и сделаем подстановку у=аох. Таким образом, мы всегда можем считать все коэффициенты цеВнлыми, а ставший равным 1.

В алгебре доказывается, что все рациональные решения такоВнго уравнения являются целыми числами, и при том делителями свободного члена. Разумеется, у уравнения могут быть и ирраВнциональные корни.

Работу можно существенно сократить, если воспользоваться модификацией схемы Горнера.

Пусть а тАФ корень уравнения, тогда по теореме Безу

xn+a1xn-1+тАж+an=(x-a)(xn-1+c1xn-2+тАж+cn-1).

Запишем это тождество в виде

xn+a1xn-1+тАж+an=(x-a)(-b0xn-1-b1xn-2-тАж-bn-1)

и приравняем коэффициенты при одинаковых степенях:

an=abn-1; an-1=abn-2-bn-1; тАж;a1=ab0-b1; 1=-b0

Все числа ai и bi являются целыми, поэтому an,an-1+bn-1,тАж делятся на а. Значит, если хоть один из коэффициентов bi окаВнжется нецелым, то проверяемое число не может быть корнем. ОтВнметим также, что по теореме Безу при x=1 и х=-1 a0+a1+тАж+an делится на а-1, а ao-a1+тАж+(В±)an делится на а+1. Обе суммы вычисляются один раз в начале работы. Эти два условия позволяют сразу отбросить ВллишниеВ» делители.

В более общем виде этот метод позволяет находить разложеВнние на множители многочлена с рациональными коэффициентами.

Пусть f (х)тАФмногочлен с целыми коэффициентами. ПредпоВнложим, что он является произведением многочленов g (х) и Н (х). При любом целом х из f (x)=g (х) h (х) следует, что f (х) делится на g(x). Пусть ттАФстепень многочлена g(x). Возьмем m+l различВнных целых значений х, например 0,1тАФ1,2.. g (х) вполне задается своими значениями в этих точках, которые являются делителями значений f (х) в тех же точках. Итак, все возможные делители стеВнпени не выше m с целыми коэффициентами многочлена f (х) опреВнделяются различными комбинациями делителей чисел f (0), f (1), f (-1),.. .

Не разбирая алгоритм подробно, перечислим основные этапы работы.

1. Вычислить f (0), f (1), .. (m+1тАФзначение) (если f (х)тАФ многочлен степени n, то т достаточно взять равным п/2).

2. Рассмотреть все возможные комбинации делителей f (0), f (1), .., взятых с обоими знаками.

3. Для каждой комбинации (do, d1, .., dm) найти коэффициенты многочлена g (х), принимающего в точках 0,1,-1.. значения do, d1, .., dm.

4. Если f (х) делится нацело на g (х), то задача решена, иначе перейти к анализу следующей комбинации.

Последовательно применяя этот алгоритм, можно найти разВнложение многочлена на неприводимые множители. Эта задача деВнмонстрирует связь представления многочлена как алгебраической структуры и функциональной зависимости, а также практическое приложение этой связи.

4. Комбинаторика. Одним из важнейших применений комбинаВнторики является программирование, где, например, перестановки и их свойства существенно используются для анализа различных алгоритмов сортировки информации. Сортировкой называется расположение ранее неупорядоченной информации (массива, файла) в порядке возрастания или убывания. Понятие возрастания (поВнрядка) широко применяется в моделировании конкретных задач. Кроме обычного порядка на множестве чисел Влчисло а больше числа &В», можно назвать упорядочение букв в алфавите, слов в словаре. Иногда информация упорядочивается по какой-то одной части, или, как обычно говорят, по одному полю. Например, инфорВнмация об учащихся (журнал) упорядочена по фамилиям. СчитаВнется, что в мире более четверти всего машинного времени тратится на сортировку. Поэтому важно грамотно выбирать метод сортиВнровки в зависимости от конкретной задачи, т. е. проводить анализ эффективности алгоритмов. Неупорядоченное множество можно рассматривать как некоторую перестановку упорядоченного, поэтому свойства перестановок определяют числовые характеристики алгоритмов сортировки.

Далее для простоты изложения под перестановкой понимается перестановка без повторений чисел 1, 2, .., n, обозначаемая (a1, a2, .., an). Следующие основные понятия, часто выходящие за пределы школьного курса математики, приводят к интересным алгоритмам.

Упорядочение множества перестановок. На множестве переВнстановок можно определить порядок. Будем говорить, что одна перестановка больше другой, если до какого-то элемента они совпаВндают, а следующий в первой больше, чем во второй. Например, (4, 2, 3, 1) больше, чем (4, 2, 1, 3). Такой порядок называется лексикографическим. Будем говорить, что одна перестановка неВнпосредственно следует за другой, если она больше ее, и не сущеВнствует третьей перестановки, которая была бы меньше первой, но больше второй. Вышеприведенные перестановки непосредственно следуют одна за другой. Построим алгоритм, позволяющий по данной перестановке построить непосредственно следующую. Если применить его последовательно, начиная с наименьшей перестаВнновки (1, 2, ..), то можно получить все перестановки. Такой генеВнратор перестановок может использоваться для численного анализа различных алгоритмов сортировки и во многих других прилоВнжениях.

СЛЕДУЮЩАЯ ПЕРЕСТАНОВКА.

С1. Для i от n-1 с шагом -1 до 1 выполнить

если a(i)<a(i+1) то перейти к С2.

Закончить (исходная перестановка максимальна).

С2. (найти наименьшее число, большее а (i)).

Для j от п с шагом тАФ 1 выполнить

если a(i)<a(j), то перейти к С3 (j заведомо больше i)

СЗ. Переставить а (i) и а (j)

С4. (перевернуть конец перестановки)

Для k от 1 до (n-i)/2 переставить a(i+k) и a(nтАФk+1)

Эта задача демонстрирует важное для приложений, но выходяВнщее за рамки школьного курса применение понятия порядка.

Отметим, что этот алгоритм может быть обобщен для случая перестановок с повторениями, а также для случая, когда каждый элемент имеется в неограниченном количестве экземпляров, наВнпример для генерации упорядоченных ВлсловВ» заданной длины.

Циклы. Перестановку можно рассматривать как функцию, опреВнделенную на множестве чисел (1,2, .., n) со значениями в том же множестве. Этот подход позволяет перенести на перестановки многие понятия теории функций, а также теории групп, поскольВнку перестановки с естественно определенным умножением обраВнзуют группу. Чтобы отличать этот подход от предыдущего, будем применять двустрочное обозначение

Перестановку можно задавать как произведение циклов. ВышеВнприведенная перестановка есть произведение циклов (1, 4) и (3, 2), т. е. 1 переходит в 4, 4 в 1, 2 в 3, а 3 в 2. Конечно, разложение в циклы не однозначно, поскольку ту же перестановку можно заВнписать в виде (3, 2) (4,1). Однако на самом деле это Влте же самыеВ» циклы, и можно определить понятие канонической записи, при коВнторой такое разложение будет однозначным (ср. каноническую запись многочлена). Отметим, что в канонической записи скобки можно опустить, поскольку они восстанавливаются однозначно.

Циклы применяются, если требуется произвести перестановку элементов массива, не применяя дополнительной памяти,тАФ в этом случае каждый цикл переставляется независимо по кругу.

Пусть задано некоторое произведение циклов. Как их переВнмножить? Тривиальный алгоритм прослеживает каждый элемент через все циклы. Например, если перемножаются циклы (1, 3, 6, 7) (2, 3, 4) (1, 5, 4) (6, 1, 4, 5) (2, 7), то 1 переходит в 3. 3 в 4, 4 в 1, 1 в 4, 4 неподвижно, окончательно 1 переходит в 4. Но при таком подходе придется просматривать всю формулу п раз. Существует алгоритм, позволяющий решить задачу за один просмотр формулы. Создадим вспомогательный массив Л, в начале содержащий едиВнничную перестановку (1, 2, .. п). Будем просматривать формулу с конца, т. е. справа налево. Если очередной символ не скобка, запомним его в М, а элемент, ранее находившийся в М, поместим на его место. При символе ")", отмечающем границу цикла, в М отправляем 0 и позицию следующего числа временно запомним в KС, пока не дойдем до конца цикла тАФ символа "(" и не узнаем, во что оно переходит.

ЦИКЛ.

Ц1. (создать массив A) для i от 1 до п A(i) ←i

Ц2. Взять следующий элемент (просмотр справа налево) х

если х="(", то перейти к Ц4

если х число, то перейти к Ц3(j тАФ индекс х в A)

если х=")" то M←0 и перейти к Ц2

если формула исчерпана, то закончить (AтАФ искомая перестаВнновка)

ЦЗ. если M=0 (первый элемент после ")"), то К ← j, М ←A(j), перейти к Ц2

Ц4. A (k) ←M, перейти к Ц2.

Эта задача показывает важный подход к задачам символьной обработки строк, позволяющий значительно (на порядок) сокраВнтить время работы.

Обратимся теперь к курсу геометрии. Методы аналитической геометрии, когда точка задается своими координатами, а линии и поверхности тАФ уравнениями, решениями которых являются соотВнветствующие множества точек, позволяют решать многие геометВнрические задачи с помощью ЭВМ.

5. Выпуклые фигуры. Многие приложения, например задачи линейного программирования, приводят к необходимости строить выпуклую оболочку множества точек. Для этого достаточно найти такое подмножество данного множества точек, являющихся верВншинами выпуклого многоугольника, который содержит все остальВнные точки множества. Легко доказать, что с точностью до порядка вершин такой многоугольник единствен. Точка принадлежит выВнпуклому многоугольнику, если она и все его вершины лежат по одну сторону от любого его ребра. Здесь и далее под Вллежать по одну сторонуВ» понимается принадлежность одной полуплоскости, т. е. включается и случай, когда точка лежит на прямой.

Задача построения выпуклой оболочки n точек решается по индукции. При трех точках решение очевидно. Пусть построена выпуклая оболочка первых п точек. Возьмем n +1-ю точку. Если она принадлежит построенному многоугольнику, то она не меняет выпуклой оболочки. В противном случае ее нужно включить в многоугольник. Ребра, разделяющие эту точку и вершины многоВнугольника, расположены в многоугольнике последовательно. Пусть (Ai,Ai+1) (Ai+1, Ai+2) тАж

тАж(Aj-1,Aj) тАФ такая последовательность. Если она состоит из одного ребра (Ai,Ai+1), то точка включается между вершинами Ai и Ai+1, иначе вершины Ai+1, .., Aj-1 замеВнняются на An+1. Таким образом мы можем получить выпуклую оболочку любого числа точек.

При составлении программы трудность представляет обработВнка Влзамыкания многоугольникаВ», ребра (AK,A1). Остальные ребра обрабатываются в цикле по номеру вершины. Чтобы не обрабаВнтывать данное ребро отдельно, полезно продублировать его в конВнце массива. Отметим также, что при осуществлении алгоритма приходится то вставлять очередную вершину в список вершин многоугольника, то удалять из него одну или несколько точек. Это приводит нас к проблеме хранения списка в памяти. Вершины многоугольника образуют типичный список с двумя связями тАФ предыдущая и последующая вершины. Возможно несколько ваВнриантов решения. Можно удаляемые вершины отмечать каким-либо значением, и тогда при необходимости вставить новую верВншину достаточно сдвинуть небольшой фрагмент массива до блиВнжайшего пустого места. Другой способ связан с применением таблицы ссылок.

С очевидными изменениями этот алгоритм обобщается на слуВнчай выпуклых многогранников.

Мы рассмотрели задачи из нескольких разделов математики, представляющих различные аспекты межпредметных связей курса ОИВТ и математических курсов. Методически продуманный в этом смысле отбор заданий для практики по программированию позвоВнляет наряду с изучением информатики активизировать и углубить знания учащихся по математике. При этом математические поВннятия и теоремы используются для разработки и доказательства правильности алгоритмов и для их анализа, т. е. приобретают практический, прикладной характер.

Заключение

Развитие познавательного интереса учащихся к ЭВТ, инфорВнматике, программированию тАФ задача чрезвычайной важности, от решения которой в значительной мере зависит успех овладения учащимися второй, компьютерной грамотностью.

Однако у большинства любознательных ребят интерес к ЭВМ часто сводится лишь к желанию как можно скорее Влнажимать на кнопочкиВ», Влполучать смешные картинкиВ», играть с компьютеВнром в ВлМорской бойВ»

Одной из важных форм укрепления интереса учащихся к инВнформатике является правильная мотивация. Необходимо вызвать у ребят чувство сопричастности к решению важнейших государВнственных задач, объяснить им на интересных примерах прямую связь между показателем степени развития любой страны и ее ВлинтеллектуальнымВ» потенциалом. Мотивациоиный компонент должен, по нашему мнению, в разнообразной форме присутствоВнвать не только на первых уроках, но и в течение года при решеВннии различных, в том числе профориентационных задач.

Некоторые ребята становятся не только помощниками учитеВнля, но и во многом (особенно в практических навыках) превосВнходят его. Опыт показывает, что специфика предмета информатиВнки способствует этому и начинающим учителям информатики слеВндует не огорчаться этому факту, а стремиться использовать его.

Ребята с большим интересом узнали, что написанная в 1854 г. книга Дж. Булля ВлОсновы логики высказыванийВ» за целый век до появления ЭВМ явилась незаменимым помощником в создаВннии логических элементов ЭВМ, языков программирования. На занятия по логическим элементам ЭВМ мы обычно приглашаем инженера-электронщика. Многие школьники, интересующиеся электроникой, самостоятельно готовят сообщения о работе тригВнгера, о схемах совпадения, отрицания, логического умножения, логического сложения и т. д.

Интересно, с использованием межпредметных связей, можно построить и сами уроки. Знания основ логики не только способВнствуют развитию познавательного интереса учащихся, но и заВнкладывают основы успешного овладения всем курсом информаВнтики, способствуют развитию алгоритмического мышления, в частности умению рационально строить разветвляющиеся и циклиВнческие алгоритмы, быстрейшему овладению алгоритмическим языком, помогают в овладении любыми знаниями.

Список литературы

Абрамов С.А. Математические построения и программирование.тАУ М., 1987г.
Пикан В.В. и др. Из опыта обучения геометрии в 6 классе. тАУ М., 1983г.
Брудно А.Л., Каплан Л.И. Олимпиады по программированию для школьников. тАУ М., 1985г.
Кнут Д. Искусство программирования для ЭВМ. Основные алгоритмы тАУ М., 1976г.
Кузнецов Э.И., Шерпаев Н.В. Элименты информатики на уроках геометрии. тАУ М., Просвещение 1987г.
Мейерович Л.Н. Межпредметные связи курсов ВлОИВТВ» и ВлМатематикаВ» при выборе задач для практике по программированию тАУ М., Просвещение 1987г.
Левина Е.С. Развитие познавательного интереса учащихся к информатике тАУ М., Просвещение 1987г.

Приложение

ЯЗЫК БЕЙСИК

АНГЛИЙСКИЕ СЛУЖЕБНЫЕ СЛОВА	СМЫСЛОВОЙ ПЕРЕВОД
LET	пусть
GOTO	перейти на
IF	если
THEN	то
FOR	для
TO	до
STEP	шаг
NEXT	следующий
DATA	данные
READ	читать
INPUT	Ввести
PRINT	печатать
END	конец
DIMENSION)	размерность
RUN	пуск
ERROR	ошибка
REM(ARK)	примечание
BACK SPACE	обратный ход
LINE	линия
EDIT	редактирование
RECALL	отзывать
DELETE	Вычеркивать
ERASE	стирать
INSERT	Вставить
CLEAR	очищать
ROUND	округлять
LIST	список
SELECT	Выбирать

Вместе с этим смотрят:

Основные определения и теоремы к зачету по функциональному анализу
Основные понятия математической статистики
Основные формулы
Основы математики