Поверхности второго порядка
Содержание.
- Понятие поверхности второго порядка.1. Инварианты уравнения поверхности второго порядка.
- Классификация поверхностей второго порядка.1. Классификация центральных поверхностей.
Д 1В°. Эллипсоид.
Д 2В°. Однополостный гиперболоид.
Д 3В°. Двуполостный гиперболоид.Д 4В°. Конус второго порядка.
2. Классификация нецентральных поверхностей.
Д 1В°. Эллиптический цилиндр, гиперболический цилиндр, эллиптический параболоид, гиперболичеВнский параболоид.
Д 2В°. Параболический цилиндр
тАв Исследование формы поверхностей второго порядка по их каноническим уравнениям.
- Эллипсоид.2. Гиперболоиды.
Д 1В°. Однополостный гиперболоид.
Д 2В°. Двуполостный гиперболоид.
3. Параболоиды.
Д 1В°. Эллиптический параболоид.Д 2В°. Гиперболический параВнболоид.
4. Конус и цилиндры второго порядка.
Д 1В°. Конус второго порядка.Д 2В°. Эллиптический цилиндр.Д 3В°. Гиперболический цилиндр.Д 4В°. Параболический цилиндр.
Список использованной литературы.
1. ВлАналитическая геометрияВ» В.А. Ильин, Э.Г. Позняк
Вз 1. Понятие поверхности второго порядка.Поверхность второго порядка - геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
a11х2 + а22у2 + a33z2+ 2a12xy + 2a23уz + 2a13xz + 2а14 x + 2а24у+2а34z +а44 = 0 (1)
в котором по крайней мере один из коэффициентов a11 , а22 , a33 , a12 , a23 , a13 отличен от нуля.
Уравнение (1) мы будем называть общим уравнением поВнверхности второго порядка.
Очевидно, поверхность второго порядка, рассматриваемая как геометрический объект, не меняется, если от данной деВнкартовой прямоугольной системы координат перейти к другой декартовой системе координат. Отметим, что исходное уравнеВнние (1) и уравнение, полученное после преобразования коорВндинат, алгебраически эквивалентны.
1. Инварианты уравнения поверхности второго порядка.
Справедливо следующее утверждение.
являются инвариантами уравнения (1) поверхности второго-порядка относительно преобразований декартовой системы коВнординат.
Доказательство этого утверждения приведено в выпуске ВлЛинейная алгебраВ» настоящего курса.
Вз 2. Классификация поверхностей второго порядка1. Классификация центральных поверхностей. Пусть S тАФ центральная поверхность второго порядка. Перенесем начало координат в центр этой поверхности, а затем произведем станВндартное упрощение уравнения этой поверхности. В резульВнтате указанных операций уравнение поверхности примет вид
a11х2 + а22у2 + a33z2 + а44 = 0 (2)
Так как инвариант I3 для центральной поверхности отличен от ноля и его значение, вычисленное для уравнения (2) , равно a11 тАв а22 тАв a33 , то коэффициенты a11 ,а22 , a33 удовлетворяют условию :
Возможны следующие случаи :
Д 1В°. Коэффициенты a11 ,а22 , a33 одного знака, а коэффициент а44 отличен от нуля. В этом случае поверхность S называется эллипсоидом.
Если коэффициенты a11 ,а22 , a33 , а44 одного знака, то левая часть (2) ни при каких значениях х, у, z не обращается в нуль, т. е. уравнению поверхности S не удовлетворяют коордиВннаты никакой точки. В этом случае поверхность S называется мнимым эллипсоидом.
Если знак коэффициентов a11 ,а22 , a33 противоположен знаку коэффициента а44 , то поверхность S называется вещественным эллипсоидом. В дальнейшем термином ВлэллипсоидВ» мы будем называть лишь вещественный эллипсоид.
Обычно уравнение эллипсоида записывают в канонической форме. Очевидно, числа
![]()
положительны. Обозначим эти числа соответственно а2, b2, с2. После неВнсложных преобразований уравнение эллипсоида (2) можно записать в следующей форме:
Уравнение (3) называется каноническим уравнением эллипВнсоида.
Если эллипсоид задан своим каноническим уравнением (3), то оси Ох, Оу и Оz. называются его главными осями.
Д 2В°. Из четырех коэффициентов a11 ,а22 , a33 , а44 два одного знаВнка, а два другихтАФпротивоположного. В этом случае поверхВнность S называется однополостным гиперболоидом.
Обычно уравнение однополостного гиперболоида записывают в канонической форме. Пусть, ради определенности, a11 > 0, а22 > 0, a33 < 0, а44 < 0. Тогда числа
![]()
положительны. Обозначим эти числа соответственно а2, b2, с2. После несложных преобразований уравнение (2) однополостного гиперболоида можно записать в следующей форме:
Уравнение (4) называется каноническим уравнением однопоВнлостного гиперболоида.
Если однополостный гиперболоид задан своим каноническим уравнением (4), то оси Ох, Оу и Oz называются его главВнными осями.
Д 3В°. Знак одного из первых трех коэффициентов a11 ,а22 , a33 , а44 противоположен знаку остальных коэффициентов. В этом случае поверхность S называется двуполостным гиперболоидом.
Запишем уравнение двуполостного гиперболоида в каноничеВнской форме. Пусть, ради определенности, a11 < 0, а22 < 0, a33 > 0, а44 < 0. Тогда :
![]()
Обозначим эти числа соответственно через a2, b2, с2. Поcли несложных преобразоваВнний уравнение (2) двуполостного гиперболоида можно запиВнсать в следующей форме:
Уравнение (5) называется каноническим уравнением двупоВнлостного гиперболоида.
Если двуполостный гиперболоид задан своим каноническим
уравнением, то оси Ох, Оу и Оz называются его главными осями.
Д 4В°. Коэффициент а44 равен нулю. В этом случае поверхность S называется конусом второго порядка.
Если коэффициенты a11 , а22 , a33 одного знака, то левая часть (2) обращается в нуль (а44 = 0) лишь для х=у=z=0, т. е. уравнению поверхности S удовлетворяют координаты только едной точки. В этом случае поверхность S называется мнимым конусом второго порядка. Если коэффициенты a11 , а22 , a33 имеют разные знаки, то поверхность S является вещественным конусом второго порядка.
Обычно уравнение вещественного конуса второго порядка заВнписывают в канонической форме. Пусть, ради определенности,
a11 > o, а22 > 0, a33 < 0. Обозначим
![]()
соответственно через а2, b2, с2. Тогда уравнение (2) можно записать в виде
Уравнение (6) называется каноническим уравнением вещеВнственного конуса второго порядка.
2. Классификация нецентральных поверхностей второго поВнрядка.
Пусть S тАФ нецентральная поверхность второго порядка, т. е. поверхность, для которой инвариант I3 равен нулю. Произведем стандартное упрощение уравВннения этой поверхности. В результате уравнение поверхности примет вид
aВґ11хВґ2 + аВґ22уВґ2 + aВґ33zВґ2 + 2аВґ14 xВґ + 2аВґ24уВґ+2аВґ34zВґ +аВґ44 = 0 (7)
для системы координат OxВґyВґzВґ
Так как инвариант I3 = 0 и его значение, выВнчисленное для уравнения (7) , равно
aВґ11 тАв аВґ22 тАв aВґ33 , то один или два из коэффициентов aВґ11 , аВґ22 , aВґ33 равны нулю. В соответствии с этим рассмотрим следующие возможные случаи.
Д 1В°. Один из коэффициентов aВґ11 , аВґ22 , aВґ33 равен нулю. Ради определенности будем считать, что aВґ33 = 0 (если равен нулю каВнкой-либо другой из указанных коэффициентов, то можно перейВнти к рассматриваемому случаю путем переименования осей координат). Перейдем от координат х', у', z' к новым координатам х, у, z по формулам
Подставляя х', у' и z', найденные из (8), в левую часть (7) и заменяя затем
aВґ11 на a11 , аВґ22 на а22 , аВґ34 на p и аВґ44 на q , получим следующее уравнение поверхности S в новой системе коВнординат Oxyz :
a11х2 + а22у2 + 2pz + q = 0 (9)
1) Пусть р = 0, q = 0. Поверхность S распадается на пару плоВнскостей
При этом, очевидно, эти плоскости будут мнимыми, если знаки a11 и а22 одинаковы, и вещественными, если знаки a11 и а22 различны.
2) Пусть р = 0, q тЙа 0. Уравнение (9) принимает вид
a11х2 + а22у2 + q = 0 (10)
Известно, что уравнение (10) явВнляется уравнением цилиндра с образующими, параллельными оси Оz. При этом если a11 , а22 , q имеют одинаковый знак, то левая часть (10) отлична от нуля для любых х и y, т. е. циВнлиндр будет мнимым. Если же среди коэффициентов a11 , а22 , q имеются коэффициенты разных знаков, то цилиндр будет веВнщественным. Отметим, что в случае, когда a11 и а22 имеют одинаковые знаки, a q тАФ противоположный, то величины
положительны.
Обозначая их соответственно через а2 и b2, мы приведем уравнение (10) к виду
Таким образом, в отмеченном случае мы имеем эллиптический цилиндр. В случае, a11 и а22 имеют различные знаки, мы получим гиперболический цилиндр. Легко убедиться, что уравВннение гиперболического цилиндра может быть приведено к виду
3) Пусть ртЙа0. Произведем параллельный перенос системы координат, выбирая новое начало в точке с координатами
(0, 0, ).
При этом оставим старые обозначения координат х, у, z. Очевидно, для того чтобы получить уравнение поверхВнности S в новой системе координат, достаточно заменить в уравВннении (9)
Получим следующее уравнение:
a11х2 + а22у2 + 2pz = 0 (13)
Уравнение (13) определяет так называемые параболоиды. Причем если a11 и а22 имеют одинаковый знак, то параболоид называется эллиптическим. Обычно уравнение эллиптического параболоида записывают в канонической форме:
Уравнение (14) легко получается из (13). Если a11 и а22 имеют разные знаки, то параболоид называется гиперболичеВнским. Каноническое уравнение гиперболического параболоида имеет вид
Это уравнение также легко может быть получено из (13).
Д 2В°. Два из коэффициентов aВґ11 , аВґ22 , aВґ33 равны нулю. Ради определенности будем считать, что aВґ11 = 0 и аВґ22 = 0 Перейдем от х,', у', z' к. новым координатам х, у, z по формулам :
Подставляя х', у' и z' , найденные из (16) в левую часть (7) и заменяя затем aВґ33 на a33 , aВґ14 на р , aВґ24 на q и aВґ44 на r , поВнлучим следующее уравнение поверхности S в новой системе коВнординат Охуz :
a33 z2 + 2px + 2qy + r = 0 (17)
1) Пусть р=0, q=0. Поверхность S распадается на пару паВнраллельных плоскостей
При этом, очевидно, эти плоскости будут мнимыми, если знаки a33 и r одинаковы, и вещественными, если знаки a33 и r различВнны, причем при r = 0 эти плоскости сливаются в одну.
2) Хотя бы один из коэффициентов р или q отличен от нуля. В этом случае повернем систему координат вокруг оси Oz так, чтобы новая ось абсцисс стала параллельной плоскости 2рх+2qy+r=0. Легко убедиться, что при таком выборе системы координат, при условии сохранения обозначения х, у и z для новых координат точек, уравнение (17) примет вид
a33 z2 + 2qВґy = 0 (19)
которое является уравнением параболического цилиндра с обраВнзующими, параллельными новой оси Ох.
Вз 3. Исследование формы поверхностей второго порядка по их каноническим уравнениям1. Эллипсоид.
Из уравнения (3) вытекает, что координатные плоскости явВнляются плоскостями симметрии эллипсоида, а начало коордиВннаттАФцентром симметрии. Числа а, b, с называются полуосями эллипсоида и представляют собой длины отрезков, от начала координат до точек пересечения эллипсоида с осями координат. Чтобы более наглядно представить себе форму эллипсоида, выясним форму линий пересечения его плоскостями, параллельными какой-либо из координатных плоскостей.
Ради определенности рассмотрим линии Lh пересечения элВнлипсоида с плоскостями
z = h (20)
параллельными плоскости Оху. Уравнение проекции L*h лиВннии Lh на плоскость Оху получается из уравнения (3), если положить в нем z = h. Таким образом, уравнение этой проекции имеет вид
Если положить
то уравнение (21) можно записать в виде
т. е. L*h представляет собой эллипс с полуосями а* и b*, которые могут быть вычислены по формулам (22). Так как Lh получается ВлподъемомВ» L*h на высоту h по оси Оz (см. (20)), то и Lh представляет собой эллипс.
Представление об эллипсоиде можно получить следующим обВнразом. Рассмотрим на плоскости Оху семейство эллипсов (23) (рис. 1), полуоси а* и b* которых зависят от h (см. (22)), и каждый такой эллипс снабдим отметкой h, указывающей, на каВнкую высоту по оси Оz должен быть ВлподнятВ» этот эллипс. Мы получим своего рода ВлкартуВ» эллипсоида. Используя эту ВлкарВнтуВ», легко представить себе пространственный вид эллипсоида.
(Метод представления формы фигуры путем получения ВлкартыВ» фигуры я привожу только для эллипсоида, представить форму других фигур этим методом можно аналогично)
Наглядное изображение эллипсоида находится на следующей странице.
Эллипсоид .
2. Гиперболоиды.
Д 1В°. Однополостный гиперболоид. Обратимся к каноническому
уравнению (4) однополостного гиперболоида
Из уравнения (4) вытекает, что координатные плоскости явВнляются плоскостями симметрии, а начало координат тАФ центром симметрии однополостного гиперболоида.
Д 2В°. Двуполостный гиперболоид. Из канонического уравнения (5) двуполостного гиперболоида вытекает, что координатные плоВнскости являются его плоскостями симметрии, а начало коордиВннат тАФ его центром симметрии.
3. Параболоиды.
Д 1В°. Эллиптический параболоид. Обращаясь к каноническому уравнению (14) эллиптического параболоида
мы видим, что для него Oxz и Оуz являются плоскостями симметрии. Ось Oz, представляющая линию пересечения этих плоскостей, называется осью эллиптического параболоида.
Д 2В°. Гиперболический параВнболоид. Из канонического уравнения (15) гиперболического параболоиВнда вытекает, что плоскости Oxz и Оуz являются плоскоВнстями симметрии. Ось Oz называется осью гиперболического пaраболоида.
Прим.: получение Влкарты высотВ» для гиперболического пaраболоида несколько отличается от аналогичной процедуры для вышеприведенных поверхностей 2-го порядка, поэтому я также включил его в свой реферат.
Линии z=h пересечения гиперболического параболоида плоскостями z=h представляют собой при h>0 гиперболы
с полуосями
а при h < 0 тАФсопряженные гиперболы для гипербол (24)
с полуосями
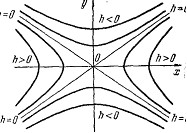
Используя формулы (24)тАФ(27), легко построить ВлкартуВ» гиперболического параболоида. Отметим еще, плоскость z=0 пересекает гиперболический параболоид по двум прямым :
Из формул (25) и (27) вытекает, что прямые (28) являются асимптотами гипербол (24) и (26).Карта гиперболического параболоида дает представление о его пространственной форме. Как и в случае эллипВнтического параболоида, можно убедиться в том, что гиперболиВнческий параболоид может быть получен путем параллельного перемещения параболы, предстаВнвляющей собой сечение плоскоВнстью Oxz (Оуz), когда ее верВншина движется вдоль параболы, являющейся сечением параболоВнида плоскостью Oyz (Oxz).
Прим.: Изображение гиперболического пaраболоида дано на следующей странице.
Гиперболический параВнболоид.4. Конус и цилиндры второго порядка.
Д 1В°. Конус второго порядка
Убедимся, что вещественный конус S образован прямыми лиВнниями, проходящими через начало О координат. Естественно наВнзывать точку О вершиной конуса.
Для доказательства сформулированного утверждения, очевидВнно, достаточно установить, что прямая L, соединяющая произвольную, отличную от начала координат точку М0(х0, у0, z0) коВннуса (6) и начало координат О , целиком располаВнгается на конусе, т. е. координаты (х, у, z) любой точки М прямой L удовлетворяют уравнению (6).
Так как точка М0(х0, у0, z0) лежит на конусе (6), то :
Координаты (х, у, z) любой точки М прямой L равны соответВнственно tx0 , ty0 , tz0 , где tтАФнекоторое число. Подставляя эти значения для х, у и z в левую часть (6), вынося затем t2 за скобВнку и учитывая (29), мы убедимся в том, что М лежит на коВннусе. Таким образом, утверждение доказано. Представление о форме конуса может быть получено методом сечений. Легко убедиться, что сечения конуса плоскостями z = h представляют собой эллипсы с полуосями :
Д 2В°. Эллиптический цилиндр.
Состоит из прямых линий, параллельных оси Oz .
Д 3В°. Гиперболический цилиндр.
Состоит из прямых линий, параллельных оси Oz .
Д 4В°. Параболический цилиндр.a33 z2 + 2qВґy = 0 (19)Путем переименования осей координат и простых арифметических операций из уравнения, (19) мы получим новое, компактное уравнение параболического цилиндра.
![]()
Вместе с этим смотрят:
Полиномы ЧебышеваПолучение уравнения переходного процесса
Понятие о центре тяжести
Поперечные сечения и их геометрические характеристики