Применение графиков в решении уравнений
ПРИМЕНЕНИЕ ГРАФИКОВ В РЕШЕНИИ УРАВНЕНИЙ
Основная часть:
Применение графиков в решении уравнений
I)Графическое решение квадратного уравнения:
Рассмотрим приведённое квадратное уравнение : x2+px+q=0;
Перепишем его так:x 2 =-px-q.(1)
Построим графики зависимостей:y=x 2 и y=-px-q
График первой зависимости нам известен, это есть парабола; вторая зависимость- линейная; её график есть прямая линия. Из уравнения (1) видно, что в том случае, когда х является его решением, рдинаты точек обоих графиков равны между собой. Значит, данному значению х соответствует одна и та же точка как на параболе, так и на прямой, то есть парабола и прямая пересекаются в точке с абциссой х
Отсюда следующий графический способ решения квадратного уравнения:чертим параболу у=х 2 , чертим(по точкам) прямую у=-рх-q
Если прямая и парабола пересекаются, то абциссы точек пересечения являются корнями квадратного уравнения. Этот способ удобен, если не требуется большой точности
Примеры:
1.Решить уравнение:4x 2 -12x+7=0
Представим его в виде x 2 =3x-7/4
Построим параболу y=x 2 и прямую y=3x-7/4
Рисунок 1
Для построения прямой можно взять, например, точки(0;-7/4) и (2;17/4).Парабола и прямая пересекаются в двух точках с абциссами x 1 =0.8 и x 2 =2.2 (см. рисунок 1)
2.Решить уравнение : x 2 -x+1=0
Запишем уравнение в виде: x 2 =x-1
Построив параболу у=х 2 и прямую у=х-1, увидим, что они не пересекаются(рисунок 2), значит уравнение не имеет корней
Рисунок 2
Проверим это. Вычислим дискриминант:
D=(-1)2-4=-3<0,
А поэтому уравнение не имеет корней
3. Решить уравнение: x 2 -2x+1=0
Рисунок 3
Если аккуратно начертить параболу у=х 2 и прямую у=2х-1, то увидим, что они имеют одну общую точку(прямая касается параболы, см. рисунок 3), х=1, у=1;уравнение имеет один корень х=1(обязательно проверить это вычислением). 
II) Системы уравнений
Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство. Графики уравнений с двумя переменными весьма разнообразны. Например, графиком уравнения 2х+3у=15 является прямая, уравнения у=0.5х 2 тАУ2 тАУпарабола, уравнения х 2 +у 2 =4 тАУ окружность, и т.д
Степень целого уравнения с двумя переменными определяется так же, как и степень целого уравнения с одной переменной. Если левая часть уравнения с двумя переменными представляет собой многочлен стандартного вида, а правая число 0, то степень уравнения считают равной степени многочлена. Для того чтобы выяснить, какова степень какого-либо уравнения с двумя переменными, его заменяют равносильным уравнением, левая часть которого тАУ многочлен стандартного вида, а правая- нуль. Рассмотрим графический способ решения
Пример1:решить систему тМа x 2 +y 2 =25 (1)
тМаy=-x 2 +2x+5 (2)
Построим в одной системе координат графики уравнений(Рисунок4):
Построим в одной системе координат графи) 
х 2 +у 2 =25 и у=-х 2 +2х+5
Координаты любой точки построенной окружности являются решением уравнения 1, а координаты любой точки параболы являются решением уравнения 2. Значит, координаты каждой из точек пересечения окружности и параболы удовлетворяют как первому уравнению системы, так и второму, т.е. являются решением рассматриваемой системы. Используя рисунок, находим приближённые значения координат точек пересечения графиков: А(-2,2; -4,5), В(0;5), С(2,2;4,5), D(4;-3).Следовательно, система уравнений имеет четыре решения:
х1тЙИ-2,2 , у1тЙИ-4,5; х2тЙИ0, у2тЙИ5;
х3тЙИ2,2 , у3тЙИ4,5; х4тЙИ4, у4тЙИ-3
Подставив найденные значения в уравнения системы, можно убедиться, что второе и четвёртое из этих решений являются точными, а первое и третье тАУ приближёнными
III)Тригонометрические уравнения:
Тригонометрические уравнения решают как аналитически, так и графически. Рассмотрим графический способ решения на примере
Рисунок5
Пример1:sinx+cosx=1. Построим графики функций y=sinx u y=1-cosx.(рисунок 5)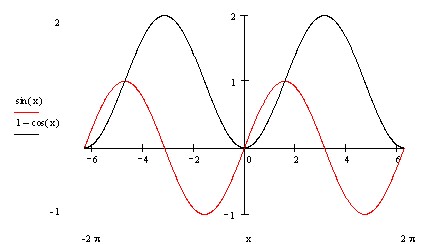 
Из графика видно, что уравнение имеет 2 решения: х=2ПАп,где пРДZ и х=ПА /2+2ПА k,где kРДZ(Обязательно проверить это вычислениями). Рисунок 6
Пример2:Решить уравнение:tg2x+tgx=0. Решать это уравнение будем по принципу решения предыдущего. Сначала построим графики(См. рисунок 6)функций: y=tg2x u y=-tgx. По графику видно что уравнение имеет 2 решения: х=ПАп, пРДZ u x=2ПАk/3, где kРДZ.(Проверить это вычислениями)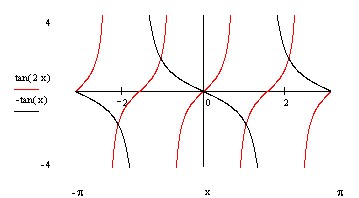 
Ва
Применение графиков в решении неравенств
1)Неравенства с модулем
Пример1
Решить неравенство |x-1|+|x+1|<4
На интеграле(-1;-тИЮ) по определению модуля имеем |х-1|=-х+1,|х+1|=-х-1, и, следовательно, на этом интеграле неравенство равносиьно линейному неравенству тАУ2х<4,которое справедливо при х>-2. Таким образом, в множество решений входит интеграл(-2;-1).На отрезке [-1,1] исходное неравенство равносильно верному числовому неравенству 2<4.Поэтому все значения переменной, принадлежащие этому отрезку, входят в множество решний
На интеграле (1;+тИЮ) опять получаем линейное неравенство 2х<4, справедливое при х<2. Поэтому интеграл (1;2) также входит в множество решений. Объединяя полученные результаты, делаем вывод: неравенству удовлетворяют все значения переменной из интеграла (-2;2) и только они
Однако тот же самый результат можно получить из наглядных и в то же время строгих геометрических соображений. На рисунке 7 построены графики функций: y=f(x)=|x-1|+|x+1| и y=4
Рисунок 7
На интеграле (-2;2) график функции y=f(x) расположен под графиком функции у=4, а это означает, что неравенство f(x)<4 справедливо. Ответ:(-2;2)
II)Неравенства с параметрами
Решение неравенств с одним или несколькими параметрами представляет собой, как правило, задачу более сложную по сравнению с задачей, в которой параметры отсутствуют
Например, неравенствотИЪа+х+тИЪа-х>4, содержащее параметр а, естественно, требует, для своего решения гораздо больше усилий, чем неравенство тИЪ1+х + тИЪ1-х>1
Что значит решить первое из этих неравенств? Это, по существу, означает решить не одно неравенство, а целый класс, целое множество неравенств, которые получаются, если придавать параметру а конкретные числовые значения. Второе же из выписанных неравенств является частным случаем первого, так как получается из него при значении а=1
Таким образом, решить неравенство, содержащее параметры, это значит определить, при каких значениях параметров неравенство имеет решения и для всех таких значений параметров найти все решения
Пример1:
Решить неравенство|х-а|+|х+а|<b, a<>0
Для решения данного неравенства с двумя параметрами a u b воспользуемся геометрическими соображениями. На рисунке 8 и 9 построены графики функций
Y=f(x)=|x-a|+|x+a| u y=b
Очевидно, что при b<=2|a| прямая y=b проходит не выше горизонтального отрезка кривой y=|x-a|+|x+a| и, следовательно, неравенство в этом случае не имеет решений (рисунок 8). Если же b>2|a|, то прямая y=b пересекает график функции y=f(x) в двух точках (-b/2;b) u (b/2;b)(рисунок 6) и неравенство в этом случае справедливо при тАУb/2<x<b/2,так как при этих значениях переменной кривая y=|x+a|+|x-a| расположена под прямой y=b
Ответ:Если b<=2|a| , то решений нет,
Если b>2|a|, то x тВм (-b/2;b/2)
III) Тригонометрические неравенства:
При решении неравенств с тригонометрическими функциями существенно используется периодичность этих функций и их монотонность на соответствующих промежутках. Простейшие тригонометрические неравенства. Функция sin x имеет положительный период 2ПА. Поэтому неравенства вида: sin x>a, sin x>=a,
sin x<a, sin x<=a
Достаточно решить сначала на каком-либо отрезке лдины 2ПА. Множество всех решений получим, прибавив к каждому из найденных на этом отрезке решений числа вида 2ПАп, пРДZ
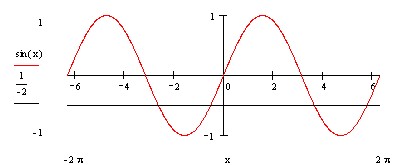
Пример 1: Решить неравенство sin x>-1/2.(рисунок 10)
Сначала решим это неравенство на отрезке[-ПА /2;3ПА/2]. Оа ассмотрим его левую часть тАУ отрезок [-ПА /2;3ПА/2].ОЧ десь уравнение sin x=-1/2 имеет одно решение х=- ПА/6; О° функция sin x монотонно возрастает. Значит, если тАУПА/2<=x<= - ПА /6, то sin x<=sin(-ПА/6)=-1/2 , т.е. эти значения х решениями неравенства не являются. Если же тАУПА/6<х<= ПА /2 то sin x>sin(- ПА /6) = тАУ1/2. Все эти значения х не являются решениями неравенства
На оставшемся отрезке [ПА /2;3ПА/2] ПД ункция sin x монотонно убывает и уравнение sin x = -1/2 имеет одно решение х=7ПА/6. Следовательно, если ПА/2<=x<7 ПА /, то sin x>sin(7 ПА /6)=-1/2, т.е. все эти значения х являются решениями неравенства. Для x РД[7 ПА /6;3 ПА /2] имеем sin x<= sin(7 ПА /6)=-1/2, эти значения х решениями не являются . Таким образом, множество всех решений данного неравенства на отрезке [-ПА /2;3ПА/2] Оµ сть интеграл (-ПА /6;7ПА/6)
В силу периодичности функции sin x с периодом 2ПА значения х из любого интеграла вида: (- ПА/6+2ПАn;7ПА/6 +2ПАn),nяг№ Z, также являются решениями неравенства. Никакие другие значения х решениями этого неравенства не являются
Ответ: -ПА /6+2ПА n<x<7 ПА /6+2 ПА n, где nРДZ
Рисунок 10
Вместе с этим смотрят:
Применение двойных интегралов к задачам механики и геометрииПрименение квадратурной формулы Чебышева для вычисления определенного интегралаПрименение тройных и кратных интеграловПрименение тройных или кратных интегралов