Сфера
Сфера и шар
Работа ученика 11 класса
средней школы №1906
юго-западного округа
г.Москвы
Кашина Виталия.
Сфера и шар.
Сфера-это фигура, состоящая из всех точек пространства, удаВнлённых от данной точки на данном расстоянии.
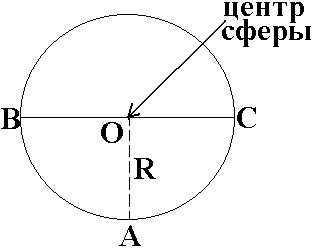
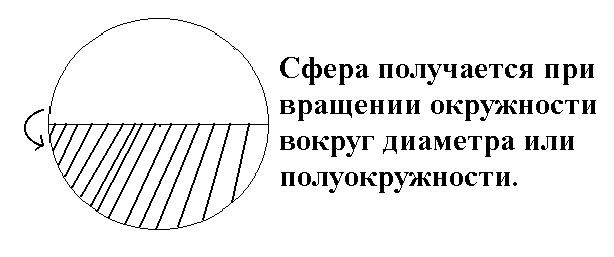
Точка О называется центром сферы, R-радиус сферы.
Любой отрезок, соединяющий центр и какую-нибудь точку сферы, называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметВнром сферы.
Шар-это фигура, состоящая из всех точек пространства, нахоВндящихся на расстоянии не большем данного от данной точки
(или фигура, ограниченная сферой).
Уравнение сферы.
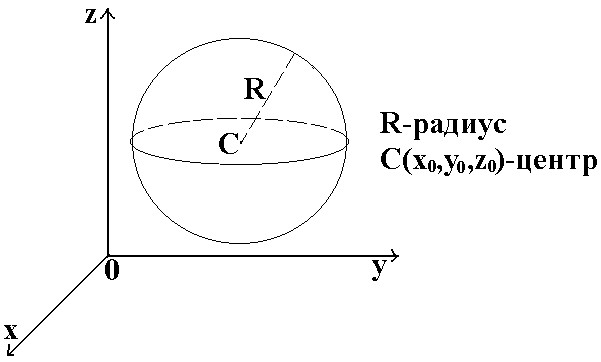
M(x;y;z)-произвольная точка, принадлежащая сфере.
след. MC=![]() т.к. MC=R, то
т.к. MC=R, то ![]()
если т.М не лежит на сфере, то MC![]() R, т.е. координаты точки М
R, т.е. координаты точки М
не удовлетворяют уравнению.Следовательно, в прямоугольной системе координат уравнение сферы радиуса R с центром C(x0;y0;z0;) имеет вид :
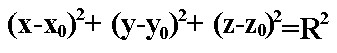
Взаимное расположение сферы и плоскости.
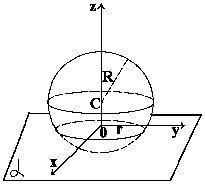
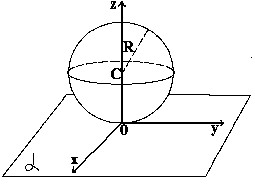
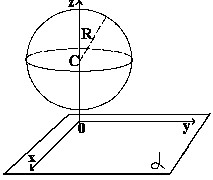
d - расстояние от центра сферы до плоскости.
след. C(0;0;d), поэтому сфера имеет уравнение ![]()
плоскость совпадает с Оxy, и поэтому её уравнение имеет вид z=0
Если т.М(x;y;z) удовлетворяет обоим уравнениям, то она лежит и в плосВнкости и на сфере, т.е. является общей точкой плоскости и сферы.
след. возможны 3 решения системы :
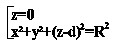
1) d<R , d^2<R^2 , x^2 + y^2 = R^2 - d^2 > 0
уравнение имеет б.м. решений, пересечение сферы и плоскости - окружВнность C(0;0;0) и r^2=R^2 - d^2
2) d=R , x^2 + y^2 =0 , x=y=0 след. сфера пересекается плоскостью в точке О(0;0;0)
3) d>R , d^2>R^2 R^2 - d^2 < 0
x^2 + y^2 >=0 , x^2+y^2=R^2 - d^2 не имеет решений
Касательная плоскость к сфере.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой каВнсания плоскости и сферы.
Теорема:
Радиус сферы, проведённый в точку касания сферы и плоскости, перпенВндикулярен к касательной плоскости.
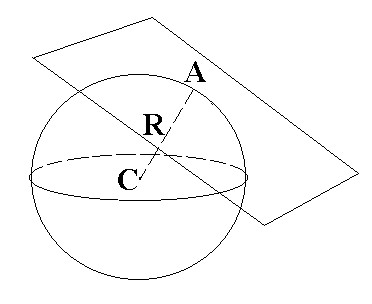
Доказательство:
Предположим, что ОА не перпендикулярен плоскости, след. ОА-наклонная к плоскости, след. ОА > R , но т.А принадлежит сфере, то получаем противоречие, след. ОА перпендикулярен плоскости.
ч.т.д.
Теорема:
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
Доказательство:
Из условия теоремы следует, что данный радиус является перпендикуВнляром, проведённым из центра сферы к данной плоскости. Поэтому расВнстояние от центра сферы до плоскости равно радиусу сферы, и, следоваВнтельно, сфера и плоскость имеют только одну общую точку. Это означает, что данная плоскость является касательной к сфере.
ч.т.д.
Площадь сферы:
Для определения площади сферы воспользуемся понятием описанного многогранника. Многогранник называется описанным около сферы (шара) , если сфера касается всех его граней. При этом сфера называется вписанной в многогранник.
Пусть описанный около сферы многогранник имеет n-граней. Будем неВнограниченно увеличивать n таким образом, чтобы наибольший размер кождой грани стремился к нулю. За площадь сферы примем предел послеВндовательности площадей поверхностей описанных около сферы многоВнгранников при стремлении к нулю наибольшего размера кождой грани. Можно доказать, что этот предел существует, и получить формулу для выВнчесления площади сферы радиуса R :
S=4ПR^2
Вместе с этим смотрят:
Тезис Геделя. Теорема ЧерчаТела вращения
Теорема о двух прямых, перпендикулярных плоскости
Теорема о противолежащих гранях параллелепипеда