Элементарные конформные отображения
ЕЛЕЦ
ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ.
КУРСОВАЯ РАБОТА
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Тема: ВлЭлементарные конфортные отображенияВ»
Выполнила: студентка группы М-31
физико-математического факультета
Е.Г. Петренко
Научный руководитель:
О.А. Саввина
1998 г.
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
Краткая справка. Пусть имеются два множества комплексных точек ![]() и
и ![]() . Если задан закон
. Если задан закон ![]() , ставящий в соответствие каждому
, ставящий в соответствие каждому ![]() точку (или точки)
точку (или точки) ![]() , то говорят, что на множестве
, то говорят, что на множестве ![]() задана функция комплексной переменной со значениями в множестве
задана функция комплексной переменной со значениями в множестве ![]() . Обозначают это следующим образом:
. Обозначают это следующим образом: ![]() . (Часто говорят также, что
. (Часто говорят также, что ![]() отображает множество
отображает множество ![]() в множество
в множество ![]() .)
.)
Задание функции ![]() эквивалентно заданию двух действительных функций
эквивалентно заданию двух действительных функций ![]() и тогда
и тогда ![]() , где
, где ![]() ,
, ![]() . Как и в обычном анализе, в теории функций комплексной переменной очень важную роль играют элементарные функции. Рассмотрим некоторые из них.
. Как и в обычном анализе, в теории функций комплексной переменной очень важную роль играют элементарные функции. Рассмотрим некоторые из них.
1. ![]()
![]() - линейная функция. Определена при всех
- линейная функция. Определена при всех ![]() . Отображает полную комплексную плоскость
. Отображает полную комплексную плоскость ![]() на полную комплексную плоскость
на полную комплексную плоскость ![]() . Функция
. Функция ![]() и обратная ей
и обратная ей ![]() - однозначны. Функция
- однозначны. Функция ![]() поворачивает плоскость
поворачивает плоскость ![]() на угол, равный
на угол, равный ![]() , растягивает (сжимает) ее в
, растягивает (сжимает) ее в ![]() раз и после этого осуществляет параллельный сдвиг на величину
раз и после этого осуществляет параллельный сдвиг на величину ![]() . Непрерывна на всей комплексной плоскости.
. Непрерывна на всей комплексной плоскости.
2. ![]() . Определена на всей комплексной плоскости, причем
. Определена на всей комплексной плоскости, причем ![]() ,
, ![]() . Однозначна, непрерывна всюду, за исключением точки
. Однозначна, непрерывна всюду, за исключением точки ![]() . Отображает полную комплексную плоскость
. Отображает полную комплексную плоскость ![]() на полную комплексную плоскость
на полную комплексную плоскость ![]() , причем точки, лежащие на единичной окружности, переходят в точки этой же окружности. Точки, лежащие внутри окружности единичного радиуса, переходят в точки, лежащие вне ее, и наоборот.
, причем точки, лежащие на единичной окружности, переходят в точки этой же окружности. Точки, лежащие внутри окружности единичного радиуса, переходят в точки, лежащие вне ее, и наоборот.
3. ![]() - показательная функция. По определению
- показательная функция. По определению ![]() , т.е.
, т.е. ![]() ,
, ![]() ,
, ![]() . Из определения вытекают формулы Эйлера:
. Из определения вытекают формулы Эйлера:
![]() ;
; 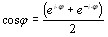 ;
; 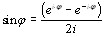 ;
;
Определена на всей комплексной плоскости и непрерывна на ней. ![]() периодична с периодом
периодична с периодом ![]() . Отображает каждую полосу, параллельную оси
. Отображает каждую полосу, параллельную оси ![]() , шириной
, шириной ![]()
![]() в плоскости
в плоскости ![]() в полную комплексную плоскость
в полную комплексную плоскость ![]() . Из свойств
. Из свойств ![]() отметим простейшие:
отметим простейшие: ![]() ,
, ![]()
4. ![]() - логарифмическая функция (натуральный логарифм). По определению:
- логарифмическая функция (натуральный логарифм). По определению: ![]() .
. ![]() Выражение
Выражение ![]() называется главным значением
называется главным значением ![]() , так что
, так что ![]() . Определен для всех комплексных чисел, кроме
. Определен для всех комплексных чисел, кроме ![]() .
. ![]() - бесконечно-значная функция, обратная к
- бесконечно-значная функция, обратная к ![]() .
. ![]() ,
, ![]()
5. ![]()
![]() - общая показательная функция. По определению,
- общая показательная функция. По определению, ![]() . Определена для всех
. Определена для всех ![]() , ее главное значение
, ее главное значение ![]() , бесконечно-значна.
, бесконечно-значна.
6. Тригонометрические функции ![]() ;
;![]() ;
;![]() ;
;![]() По определению,
По определению, 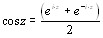 ;
; 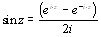 ;
;
![]() ;
; ![]()
7. Гиперболические функции. Определяются по аналогии с такими же функциями действительной переменной, а именно:
![]() ,
, ![]()
Определены и непрерывны на всей комплексной плоскости.
Задачи с решением.
1) Найти модули и главные значения аргументов комплексных чисел: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
Решение. По определению, ![]() ,
,![]() ,
, ![]() ; если
; если ![]() , то очевидно,
, то очевидно, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Найти суммы:
1) ![]()
2) ![]()
Решение. Пусть: ![]() , а
, а
![]() . Умножим вторую строчку на
. Умножим вторую строчку на ![]() , сложим с первой и, воспользовавшись формулой Эйлера, получим:
, сложим с первой и, воспользовавшись формулой Эйлера, получим: 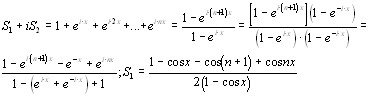
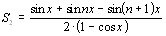 ; Преобразуя, получим:
; Преобразуя, получим:
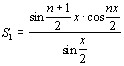 ,
, 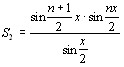
3. Доказать, что: 1) ![]() 2)
2)![]()
3)![]() 4)
4)![]()
Доказательство:
1) По определению, ![]()
2) 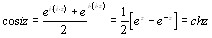
3) ![]() ;
; ![]()
Выразить через тригонометрические и гиперболические функции действительного аргумента действительные и мнимые части, а также модули следующих функций: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
;
Решение: ![]() и, учитывая результаты предыдущего примера, получим:
и, учитывая результаты предыдущего примера, получим:
![]() ,
, ![]() ,
, ![]() ,
,
![]()
Напомним, что ![]()
2) ![]()
![]() ,
, ![]() ,
,
![]()
3) 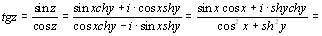
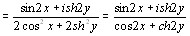 ,
, 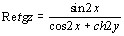 ,
,
![]() ,
, 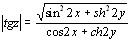 .
.
Найти действительные и мнимые части следующих значений функций: ![]() ;
; ![]() ;
; ![]()
Решение. Следуя решению примера 4, будем иметь:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]()
Вычислить: 1) ![]() ; 3)
; 3) ![]() ; 5)
; 5) ![]() ;
;
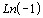 ; 4)
; 4) 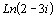 ; 6)
; 6) 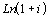 ;
;
Решение. По определению, ![]() ,
, ![]()
1)![]() ,
, ![]() ,
, ![]() ,
,
![]()
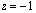 ,
, 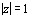 ,
, 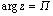 ,
,
![]()
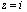 ,
, 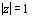 ,
, 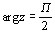 ,
, 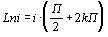
4)![]() ,
, ![]() ,
, ![]() ,
,
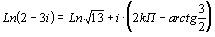
5)![]() ,
, ![]() ,
, ![]() ,
,
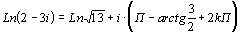
6)![]() ,
, ![]() ,
, ![]() ,
, ![]()
Найти все значения следующих степеней:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3)![]() ; 4)
; 4)![]() ;
;
Решение. Выражение ![]() для любых комплексных
для любых комплексных ![]() и
и ![]() определяются формулой
определяются формулой ![]()
1) ![]()
2)![]()
3) ![]()
4) ![]() .
.
8. Доказать следующие равенства:
1) ![]() ;
;
2) ![]() ;
;
3) ![]()
Доказательство: 1) ![]() , если
, если ![]() , или
, или ![]() , откуда
, откуда ![]() , или
, или ![]() .
.
Решив это уравнение, получим ![]() , т.е.
, т.е. ![]() и
и ![]()
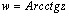 , если
, если 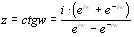 , откуда
, откуда 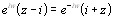 , или
, или 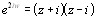 , следовательно,
, следовательно,
![]() ,
, ![]()
3) ![]() , если
, если ![]() , откуда
, откуда ![]() , или
, или
![]() .
.
Отсюда ![]() , следовательно,
, следовательно, ![]()
Вместе с этим смотрят:
Абу Али Хусейн ибн-Абдаллах ибн-Али ибн-СинаАварийная сигнализация в живом организме
Австралийский клещевой риккетсиоз
Автомобильная травма