Об энтропийной оценке сверхпластичности

Я. И. Рудаев, Е. Н. Шестаева

Кыргызско-Российский Славянский Университет, Бишкек

Рассматривается задача соответствия модели сверхпластичности процессу деформации с размытым фазовым переходом. Показано, что в оптимальных термодинамических режимах сверхпластичности минимизируется производство энтропии, которому соответствует формирование равноосной ультрамелкозернистой структуры.

Эффект сверхпластичности металлов и сплавов внешне проявляется в форме аномального квазиоднородного удлинения при малых значениях напряжений пластического течения. Металловедческими исследованиями установлено [1,2], что специфика подобной аномалии заключается в превалировании механизма зернограничного проскальзывания над другими формами массопереноса. Реализации указанного механизма способствует формирование ультрамелкозернистой структуры на предварительном этапе (структурная или микрозеренная сверхпластичность) или в процессе нагрева и деформации (динамическая сверхпластичность). Очевидно, что динамическая сверхпластичность имеет место в промышленных металлических материалах, которые реагируют на изменение температурных и кинематических условий в виде различной природы структурных превращений [3]. В частности, промышленные алюминиевые сплавы в исходном литом и деформированном состояниях проявляют сверхпластические свойства в термомеханических режимах структурного фазового перехода тАУ динамической рекристаллизации [3 тАж 8]. В процессе последней в материале возникает равновесная структура с очень мелким зерном, примерно совпадающим по размерам с субзернами. Так создается структурная ситуация, способствующая осуществлению зернограничного проскальзывания. Наличие ультрамелкого зерна можно считать необходимым, но недостаточным условием развития эффекта. К микрозернистости следует добавить требование равноосности и несклонности к росту зерна при нагреве и деформации [2]. Важным структурным элементом считаются также границы зерен [9].

Отмеченный факт был использован при формулировке модели [10, 11], адекватно с позиций механики деформируемого твердого тела отражающей накопленные экспериментальные данные. Модель описывает поведение алюминиевых сплавов не только при сверхпластичности, но и в пограничных областях термопластичности и высокотемпературной ползучести.

Естественно оценить модель [10, 11], с точки зрения определения представляющих реальный интерес физических величин и получения дополнительной информации. Очевидно, что динамической сверхпластичности соответствует размытый фазовый переход [12] и поэтому целесообразно проследить за поведением функций отклика, которые сравнительно легко определяются при известном аналитическом выражении плотности термодинамического потенциала. К указанным функциям можно, прежде всего, отнести энтропию.

Исследование функции энтропии позволяет рассматривать процесс деформации с позиций самоорганизации диссипативных структур возрастающей сложности в неравновесных открытых системах [13].

При формулировке модели энергетическая функция состояния была принята в форме термодинамического потенциала Ландау с учетом внешнего поля

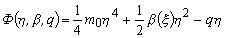. (1)

Здесь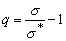; 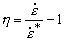- параметр порядка; 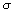- напряжение пластического течения; 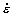- скорость деформации; 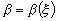- управляющий параметр; 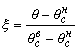- нормированная температура; 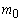- постоянная материала; причем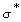, 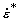- внутренние альтернативные параметры состояния; 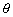- абсолютная температура; 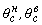- нижняя и верхняя границы термического диапазона сверхпластичности.

Легко видеть аналогию функции (1) с явным выражением потенциала катастрофы сборки [14]. Очевидно теперь, что если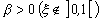, то изменений структурного характера в деформируемом материале не происходит. Условие 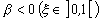соответствует структурно неустойчивому состоянию среды. Значение 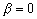отвечает переходным состояниям.

На параметр порядка накладываются следующие ограничения

на область структурных превращений

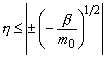; (2)

на диапазон развития сверхпластичности

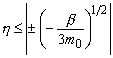. (3)

Кинетическое уравнение для управляющего параметра имеет вид

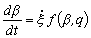, (4)

где 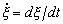- скорость возрастания нормированной температуры, 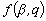- функция чувствительности среды к структурным превращениям, определяемая следующим образом

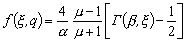, (5)

причем 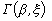- степень полноты развития фазового перехода, равная

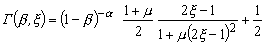; (6)

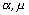- постоянные материала.

Для внутренних параметров состояния получены эволюционные уравнения

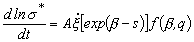, (7)

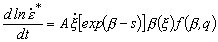, (8)

где 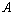- постоянная материала;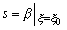, 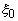- начальное значение нормированной температуры.

Уравнение состояния в соответствие (1) записывается так

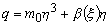. (9)

При анализе возможностей модели воспользуемся принятым в необратимой термодинамике принципом локального равновесия. В рамках этого принципа образец деформируемого материала будем, следуя [15], рассматривать как сложную систему, в каждом элементе которой имеют место известные процессы тАУ диффузионный массоперенос, движение дислокаций и зернограничное скольжение. При сверхпластичности добавляется и становится преимущественным смена соседей зерен [1,2,4] с последующими аккомодационными процессами. Возникновение сверхпластичности не происходит во всем объеме однородно деформируемого образца одновременно. Поэтому естественно предположить, что наступлению сверхпластичности предшествует метастабильное состояние, в режимах которого формируется становление механизма зернограничного проскальзывания. Зарождение указанного механизма происходит в диссипативной среде [15] и поэтому в качестве эффективного инструмента осмысление на макроуровне эффекта сверхпластичности могут быть приняты положения нелинейной неравновесной термодинамики. Заметим, что в процессе неравновесных фазовых переходов формирование новых структур не накладывается извне. Следовательно, неравновесные открытые системы могут анализироваться как термодинамически самосогласованные структуры, в которых локализован квазиравновесный термодинамический процесс. Кинетика таких структур рассматривается как переход через ряд термодинамически равновесных состояний, а зависимость системы от времени описывается через внутренние параметры состояния.

Модель (1) тАж (9), при формулировке которой использованы отмеченные положения нелинейной неравновесной термодинамики, апробирована на группе промышленных алюминиевых сплавов в исходном литом и деформированном состояниях, причем сопоставление теории и эксперимента приведено в [11].

В соответствие сказанному будем считать сверхпластичность особым состоянием деформируемого материала в иерархии состояний в меняющихся термических и кинематических условиях. Иными словами, полагаем, что имеет место процесс последовательных переходов диссипативных структур. Самоорганизация таких структур связана со стремлением открытых систем в условиях, далеких от термодинамического равновесия, к минимуму энтропии.

Функция энтропии при известной свободной энергии F определяется так

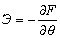. (10)

Если учесть, что плотность термодинамического потенциала и свободная энергия связаны зависимостью 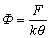(k-постоянная Больцмана), для энтропии с использованием соотношений (1)тАж(9) можем записать

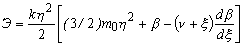, (11)

где

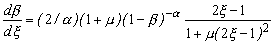. (12)

Можно показать, что в середине скоростного диапазона сверхпластичности 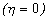энтропия обращается в нуль. При этом, как очевидно из анализа (11), функция энтропии имеет минимум при выполнении условия

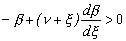. (13)

В середине термического диапазона сверхпластичност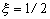и и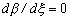. Поскольку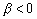, то значению параметра порядка 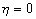соответствует наименьшее значение функции энтропии не только по скоростям деформации, но и по температурам.

Полученные данные подтверждаются формированием в оптимальных термических и кинематических режимах упорядоченной равновесной ультрамелкозернистой структуры [4].

Самоорганизация, вообще говоря, может быть вызвана различными способами [16]. Но в конкретных случаях одновременного нагрева и статического нагружения можно считать, что реализуется медленное изменение воздействия окружающей среды, при котором открытая диссипативная система переходит в новое состояние. Этот способ относится к самоорганизации через изменение управляющих параметров [16]. Взаимодействие элементов открытой системы неизбежно переносится на макро эффекты, порождаемые структурными изменениями называемые синергетическими.

Идея связать сверхпластичность с синергетикой интуитивно высказана в [17]. Подход к объяснению сверхпластичности с позиций синергетики, принятый в [18], не выходит за рамки только констатации факта формирования диссипативной структуры. Но не только в [18], но и в подавляющем большинстве оригинальных исследований сверхпластичность рассматривается отдельно, вне связи с предшествующими состояниями. Определенную негативную роль при этом играет оценка сверхпластичности по величине физически необоснованного коэффициента скоростной чувствительности, а также недостаток систематических экспериментальных данных механических исследований. Иными словами, история наступления и окончания эффекта оказывается забытой.

Полученные данные позволяют в принципе количественно оценить соответствие исследуемого явления самоорганизации диссипативных структур тАУ синергетике.

Кайбышев О.А. Сверхпластичность промышленных сплавов. - М.: Металлургия, 1984. тАУ 264с.

Новиков И. И., Портной В. К. Сверхпластичность сплавов с ультрамелким зерном. тАУ М.: Металллургия,1981. тАУ 264с.

Гуляев А. И. Сверхпластичность стали. тАУ М.: Металллургия,1982. тАУ 56с.

Вайнблат Ю.М., Шаршагин Н.А. Динамическая рекристаллизация алюминиевых сплавов // Цветные металлы. тАУ 1984.- №2. тАУ с.67-70.

Потапова Л. Л. Оценка сверхпластичности сплавов // Технология легких сплавов. тАУ 1982. - №9. тАУ с. 60-61.

Сверхпластичность некоторых алюминиевых сплавов / Ю.С.Золотаревский, В.А.Паняев, Я.И.Рудаев и др. // Судостроительная промышленность, серия материаловедение. тАУ 1990. тАУ вып.16. тАУ с.21-26.

Температурно-скоростная деформация литого алюминиевого сплава 1561 / Н. В. Жданов, В. А. Паняев, Я. И. Рудаев, Д. И. Чашников // Судостроительная промышленность, серия материаловедение тАУ 1990. Вып. 15. тАУ с.45-49.

Паняев В. А., Рудаев Я. И., Чашников Д. И. О сверхпластичности алюминиевых сплавов 1980 и В95 // Вопросы материаловедения. тАУ 1996. тАУ вып.1. тАУ с.34-38.

Кайбышев О. А., Валиев Р. З. Границы зерен и свойства металлов. тАУ М.: Металлургия, 1987. тАУ 214с.

Рудаев Я.И., Чашников Д.И. К вопросу о математическом моделировании сверхпластического одноосного растяжения // Судостроительная промышленность, серия материаловедение. тАУ 1989. тАУ вып.12. тАУ с.41-48.

Зотов В.В., Рудаев Я.И. О динамической сверхпластичности // Конверсионный потенциал Кыргызстана и проекты МНТЦ. ч.II. тАУ Бишкек, 1999.-с.186-195.

Ролов Б.Н., Юркевич В.Э. Физика размытых фазовых переходов. тАУ Ростов: РГУ, 1983. тАУ 320с.

Гленсдорф П., Пригожин И. Термодинамическая теория структуры, устойчивости, флуктуаций. тАУ М.: Мир, 1973. тАУ 280 с.

Гилмор Р. Прикладная теория катастроф. ч.I. тАУ М.: Мир, 1984. тАУ 285с.

Николис Г., Пригожин И. Познание сложного. Введение. тАУ М.: Мир, 1990. - 344с.

Хакен Г. Синергетика: иерархия неустойчивостей в самоорганизующихся системах и устройствах. тАУ М.: Мир, 1985. тАУ 423с.

Громов В. Г. О макроскопическом описании явления сверхпластичности // IV Всесоюзная конф. тАЬСверхпластичностьтАЭ (Уфа, сентябрь,1989). Тез. Докл., ч. I. тАУ Уфа: Б.Н., 1989. тАУ с.20.

Механические свойства металлов и сплавов с позиций синергетики / В. С. Иванова, Г. В. Вставский // Итоги науки и техники, материаловедение и термическая обработка. тАУ М.Ж ВИНИТИ, 1990. тАУ т. 24. С.43-98.

Вместе с этим смотрят:

"Инкарнация" кватернионов

* Алгебры и их применение

*-Алгебры и их применение

10 способов решения квадратных уравнений

Bilet