Содержание и значение математической символики

История науки показывает, что логическая структура и рост каждой математической теории, начиная с определенного этапа ее развития, становятся все в большую зависимость от использования математической символики и ее усовершенствования.

Когда индийцы в V веке н. э. ввели знак нуля, они смогли оставить поразрядную систему счисления и развить абсолютную позиционную десятичную систему счисления, превосходство которой при счете если и не осознают, то повседневно используют сотни миллионов людей. Алгебра и аналитическая геометрия обязаны многим тому, что Виет и Декарт разработали основы алгебраического исчисления. Введенные Лейбницем обозначения производной и интеграла помогли развить дифференциальное и интегральное исчисление; задачи на вычисление площадей, объемов, работы силы и т. п., решение которых раньше было доступно только первоклассным математикам, стали решаться почти автоматически. Благодаря этому обозначения Лейбница получили широкое распространение и проникли во все разделы науки, где используется математический анализ.

Пример с обозначением производной и интеграла особенно ярко подтверждает правильность замечания Л. Карно, что в математике Влсимволы не являются только записью мысли, средством ее изображения и закрепления, тАУ нет, они воздействуют на самую мысль, они, до известной степени, направляют ее, и бывает достаточно переместить их на бумаге, согласно известным очень простым правилам, для того, чтобы безошибочно достигнуть новых истинВ».

В чем заключено объективное содержание математической символики? Чем объясняется значение символики в математике?

Математические знаки служат в первую очередь для точной (однозначно определенной) записи математических понятий и предложений. Их совокупность тАУ в реальных условиях их применения математиками тАУ составляет то, что называется математическим языком.

Использование знаков позволяет формулировать законы алгебры, а также и других математических теорий в общем виде. Примером могут послужить формулы той же алгебры: (a+b)² = a² + 2ab + b²

Вах_1,2=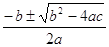Ваи т.п.

Математические знаки позволяют записывать в компактной и легкообозримой форме предложения, выражение которых на обычном языке было бы крайне громоздким. Это способствует более глубокому осознанию их содержания, облегчает его запоминание.

Математические знаки используются в математике эффективно и без ошибок, когда они выражают точно определенные понятия, относящиеся к объектам изучения математических теорий. Поэтому, прежде чем использовать в рассуждениях и в записях те или иные знаки, математик старается сказать, что каждый из них обозначает. В противном случае его могут не понять.

В связи со сказанным необходимо подчеркнуть следующее. Математики не всегда могут сказать сразу, что отражает тот или иной символ, введенный ими для развития какой-либо математической теории, средствами которой можно решать практически важные задачи. Сотни лет математики оперировали отрицательными и комплексными числами и получали с их помощью первоклассные результаты. Однако объективный смысл этих чисел и действий с ними удалось раскрыть лишь в конце XVIII и в начале XIX века. Лейбниц ввел символы dx и dy, развил дифференциальное исчисление и с помощью правил последнего показал исключительную оперативную силу этих символов. Однако Лейбниц не выявил объективного смысла знаков dx и dy; это сделали математики XIX века.

Знаки и системы знаков играют в математике роль, весьма сходную с той, какая в более широких сферах познания и практической деятельности людей принадлежит обычному разговорному языку. Подобно обычному языку, язык математических знаков позволяет обмениваться установленными математическими истинами, налаживать контакт ученых в совместной научной работе.

Решающим, однако, является то, что язык математических знаков без обычного языка существовать не может. Обычный (естественный) язык содержательнее языка математических знаков; он необходим для построения и развития языка математических знаков. Язык математических знаков только вспомогательное средство, присоединяемое к обычному языку и используемое в математике и в областях, где применяются ее методы.

Возможность использования языка знаков в математике обусловлена особенностями предмета ее исследований тАУ тем, что она изучает формы и отношения объектов реального мира, в известных границах безразличные к их материальному содержанию. Существенна при этом и специфика математических доказательств. Математическое доказательство состоит в построении цепи высказываний, начальным звеном которой являются истинные исходные предложения, конечным тАУ доказываемое утверждение. Промежуточные звенья цепи получаются в конечном счете из начального и соединяются с ним и конечным звеном с помощью законов логики и правил логического вывода. Если исходные утверждения записаны в символической форме, то доказательство сводится к их ВлмеханическимВ» видоизменениям.

Целесообразность, а в наше время и необходимость тАУ использования языка знаков в математике обусловлена тем, что при его помощи можно не только кратко и ясно записывать понятия и предложения математических теорий, но и развивать в них исчисления и алгоритмы тАУ самое главное для разработки методов математики и ее приложений. Достичь этого при помощи обычного языка если и возможно, то только в принципе, но не в практике.

Достаточная оперативность символики математической теории существенно зависит от полноты символики. Это требование состоит в том, что символика должна содержать обозначения всех объектов, их отношений и связей, необходимые для разработки алгоритмов теории, позволяющих решать любые задачи из классов однотипных задач, рассматриваемых в этой теории.

Оперирование математическими знаками есть идеализированный эксперимент: он в чистом виде описывает то, что имеет место или может быть (приближенно или точно) реализовано в действительности. Только поэтому оперирование математическими знаками способно служить открытию новых математических истин.

Решающей силой развития математической символики является не Влсвободная воляВ» математиков, а требования практики математических исследований. Именно реальные математические исследования помогают математикам в конце концов выяснить, какая система знаков наилучшим образом отображает структуру рассматриваемых количественных отношений, в силу чего может быть эффективным орудием их дальнейшего изучения.

Вз1. Введение нуля и развитие позиционной десятичной системы счисления.

Интуитивное представление о числе, по-видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей.

Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно, позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов. А за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов. Счет на бирках, по-видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета.

Важная особенность счета заключается в связи названий чисел с определенной схемой счета. Например, слово Влдвадцать триВ» тАУ не просто термин, означающий вполне определенную (по числу элементов) группу объектов; это термин составной, означающий Влдва раза по десять и триВ». Здесь отчетливо видна роль числа десять как коллективной единицы или основания; и действительно, многие считают десятками, потому что, как отметил еще Аристотель, у нас по десять пальцев на руках и на ногах.

Система счисления, которой мы в основном пользуемся сегодня, десятичная позиционная. Десятичная, так как ее основание 10. Основанием позиционной системы счисления называется возводимое в степень целое число, которое равно количеству цифр, используемых для изображения чисел в данной системе счисления. Основание показывает также, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию. В позиционных системах счисления количественный эквивалент (значение) цифры зависит от ее места (позиции) в записи числа

Десятичная система характеризуется тем, что в ней 10 единиц какого-либо разряда образуют единицу следующего старшего разряда. Другими словами, единицы различных разрядов представляют собой различные степени числа 10.

ВаДесятичной позиционной предшествовали другие, основанные на различных принципах, системы счисления. Так примером непозиционной системы (то есть такой системы, где количественный эквивалент каждой цифры не зависит от ее положения (места, позиции) в записи числа) может служить нумерация, используемая древними греками. Эта система относится к числу алфавитных. 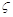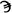Первыми восемью буквами греческого алфавита (с добавлением ВлархаичнойВ» буквы =вау, имевшей значение 6 обозначались числа от единицы до девяти, следующими восемью с добавлением =коппы, имевшей значение 90, - десятки от 10 до 90, следующими восемью с добавлением =сампи, означавшей 900, - сотни от 100 до 900, наконец, тысячи от 1000 до 9000 обозначались так же, как единицы, но со штрихом внизу: ,a означала 1000. Для того чтобы отличать числа от слов, над ними ставилась черточка. Так, число 1305 греки записывали ,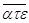. От греческой нумерации ведет свое происхождение древнерусская. Пример другой непозиционной системы дает употребляемая поныне римская нумерация.

Мы пользуемся ею для обозначения юбилейных дат, для нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т. д. В позднейшем своем виде римские цифры выглядят так: I=1; V=5; X=10; L=50; С=100; D=500; M=1000.

О происхождении римских цифр достоверных сведений нет. Цифра V могла первоначально служить изображением кисти руки, а цифра Х могла составиться из двух пятерок. Точно так же знак для 1000 мог составиться из удвоения знака для 500 (или наоборот).

Все целые числа (до 5000) записываются с помощью повторения вышеприведенных цифр. При этом если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае она не может повторяться), то меньшая вычитается из большей. Например, VI=6, т.е. 5+1, IV=4, т.е. 5-1, XL=40, т е. 50-10, LX=60, т.е. 50+10. Подряд одна и та же цифра ставится не более трех раз: LXX=70; LXXX=80; число 90 записывается ХС (а не LXXXX).

Первые 12 чисел записываются в римских цифрах так: I, II, III, IV, V, VI, VII, VIII. IX, X, XI, XII.

Примеры: XXVIII=28; ХХХIХ=39; CCCXCVII=397; MDCCCXVIII=1818.

Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Тем не менее римская нумерация преобладала в Италии до 13 века, а в других странах Западной Европы - до 16 века.

Древние египтяне использовали десятичную непозиционную систему счисления. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. Чтобы записанные таким образом числа было легко узнавать, вертикальные штрихи иногда объединялись в группы из трех или четырех черт. Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку. Множество из десяти подковообразных символов, т.е. число 100, они заменили другим новым символом, напоминающим силки; десять силков, т.е. число 1000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев тАУ волнистой линией и десять волнистых линий тАУ фигуркой удивленного человека. В итоге древние египтяне могли представлять числа до миллиона. Так, например, с помощью коллективных символов и повторений уже введенных символов число 6789 в иероглифических обозначениях можно было бы записать как

Самые древние из дошедших до нас математических записей высечены на камне, но наиболее важные свидетельства древнеегипетской математической деятельности запечатлены на гораздо более хрупком и недолговечном материале тАУ папирусе. Два таких документа тАУ папирус Ринда, или египетского писца Ахмеса (ок. 1650 до н.э.) и московский папирус, или папирус Голенищева (ок. 1850 до н.э.) тАУ служат для нас основными источниками сведений о древнеегипетских арифметике и геометрии. В этих папирусах более древнее иероглифическое письмо уступило место скорописному иератическому письму, и это изменение сопровождалось использованием нового принципа обозначения чисел. Группа одинаковых символов заменялись более простой по начертанию пометой или знаком, например, девять записывалось как Вавместо , а семьсот как Вавместо 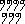. В этой записи число 6789 имело вид 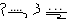, причем знаки более высокого порядка располагались справа, а не слева.

Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем счисления, так как дало возможность существенно сократить записи.

Основные недостатки непозиционных систем нумерации - трудности с изображением произвольно больших чисел и, главное, более сложный, чем в позиционных системах, процесс вычислений. (Последнее, правда, облегчалось употреблением счетных досок тАУ абаков, так что изображение чисел было необходимо лишь для конечного результата).

Крупным шагом вперед, оказавшим колоссальное влияние на все развитие математики было создание позиционных систем счисления. Первой такой системой стала вавилонская шестидесятеричная система счисления, в которой появился знак , указывающий на отсутствие разряда, выполняющего роль нашего нуля. Концевой нуль, который позволял различать, например, обозначения для 1 и 60, у вавилонян отсутствовал. Удобство вычислений в шестидесятеричной системе сделало ее популярной у греческих астрономов. К. Птолемей (II в. н.э.) при вычислениях в шестидесятеричной системе пользуется знаком Вл0В» для обозначения отсутствующих разрядов как в середине, так и в конце числа (0, омикрон тАУ первая буква греческого слова ovden-ничто). О вавилонской шестидесятеричной системе нам напоминает деление часа на 60 минут и минуты на 60 секунд, а также деление угла равного четырем прямым, на 360 градусов. Неудобство шестидесятеричной системы счисления в сравнении с десятичной тАУ необходимость большого количества знаков для обозначения индивидуальных цифр (от 0 до 59), более громоздкая таблица умножения.

Создание десятичной позиционной системы счисления, одного из выдающихся достижений средневековой науки, - заслуга индийских математиков. Позиционные десятичные записи чисел встречаются в Индии с VI в. Так, в дарственной записи 595 года встречается запись числа 346 цифрами брахми º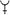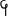(º-3, -4, 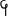-6). Первую достоверную запись нуля в виде кружочка мы находим в изображении числа 270 в настенной записи из Гвалиора, относящейся к 876г. Иногда ноль обозначался точкой. Неясно, был ли нуль собственным изобретением индийцев; возможно, они познакомились с ним по сочинениям александрийских астрономов.

Вот какова эволюция написания индийских цифр.

Вз2. Символика Виета и Декарта и развитие алгебры.

2.1 Развитие алгебры до Ф. Виета.

2.1.1 Алгебра греков.

Считается, что эллины заимствовали первые сведения по геометрии у египтян, по алгебре - у вавилонян.

В древнейших египетских источниках папирусе Райнда и Московском папирусе - находим задачи на ВлахаВ» (термин ВлахаВ» означает ВлкучаВ», ВлгрудаВ»). Имеется в виду некоторое количество, неизвестная величина, подлежащая определению) соответствующие современным линейным уравнениям, а также квадратным вида ах² = b. В вавилонских клинописных текстах имеется большое число задач, решаемых с помощью уравнений и систем первой и второй степеней, которые записаны без символов, но в специфической терминологии. В этих текстах решаются задачи, приводящие к трехчленным квадратным уравнениям вида ах² - bх = с или х² - рх = q. В задачах на ВлахаВ» можно обнаружить зачатки алгебры как науки о решении уравнений.

Но если вавилоняне за два тысячелетия до нашей эры умели числовым путем решать задачи, связанные с уравнениями первой и второй степеней, то развитие алгебры в трудах Евклида (365 - ок. 300 гг. до н. э.), Архимеда (287-212 гг. до н. э.) и Аполлония (ок. 260-170 гг. до н. э.) носило совершенно иной характер: греки оперировали отрезками, площадями, объемами, а не числами. Их алгебра строилась на основе геометрии и выросла из проблем геометрии. В XIX в. совокупность приемов древних получила название геометрической алгебры.

В качестве примера геометрической алгебры греков рассмотрим решение уравнения х² + ax = b².

Античные математики решали эту задачу построением и строили искомый отрезок так, как показано на рисунке.

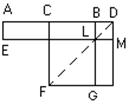
ВаНа заданном отрезке АВ (равном a) строили прямоугольник AM со сторонами (а + х) и x, равновеликий данному квадрату (b²), таким образом, чтобы избыточная над прямоугольником AL (равная ах) площадь ВМ была квадратом, по площади равным х². Сторона этого квадрата и давала искомую величину х. Такое построение называли гиперболическим приложением площади.

Далее, полагая задачу решенной, делили АВ пополам точкой С, на отрезке LM строили прямоугольник MG, равный прямоугольнику ЕС. Тогда прямоугольник AM будет разностью квадратов DF и LF. Эта разность и квадрат LF известны, поэтому по теореме Пифагора можно получить квадрат DF. После этого находили величину DC (равную ½a + x) и DB (равную х).

Геометрическое построение в точности соответствует преобразованию, с помощью которого в современных обозначениях решается уравнение указанного типа:

b² = ax + х² = тАУ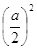

Конечно же, при таких построениях отыскивались только положительные корни уравнений: отрицательные числа появились в математике значительно позже.

С помощью геометрии древним удавалось также доказывать многие алгебраические тождества. Но каковы эти доказательства! Они безупречны в отношении логики и слишком громоздки. Вот как формулирует Евклид теорему, выражающую тождество (а + b)² = a² + 2аb + b². Если отрезок (ab) разделен в точке (g) на два отрезка, то квадрат, построенный на (ab), равен двум квадратам на отрезках (ag, gb) вместе с удвоенным прямоугольником на (ag, gb).

Естественно, связывая число с геометрическим образом (линией, поверхностью, телом), древние оперировали только однородными величинами; так, равенство было возможно для величин одинакового измерения.

Такое построение математики позволило античным ученым достигнуть существенных результатов в обосновании теорем и правил алгебры, но в дальнейшем оно стало сковывать развитие науки.

Приведенные примеры могут создать ощущение, что математика древних греков примитивна. Но это не так: созданная ими математика по своему идейному содержанию глубока и питала идеями и методами математику вплоть до XVII в. - века научной революции; многие идеи древних получили дальнейшее развитие в новой математике, созданной усилиями выдающихся умов XVIтАФXVII вв.

Накопленные в странах Древнего Востока знания состояли из набора разрозненных математических фактов, рецептур для решения некоторых конкретных задач и не могли обладать достаточной строгостью и достоверностью. Создание основ математики в том виде, к которому мы привыкли при изучении этой науки в школе, выпало на долю греков и относится к VIтАФV вв. до н. э. С этого времени начала развиваться дедуктивная математика, построенная на строгих логических доказательствах.

2.1.2 Алгебра Диофанта.

Новый подъем античной математики относится к III в. н. э., он связан с творчеством великого математика Диофанта. Диофант возродил и развил числовую алгебру вавилонян, освободив ее от геометрических построений, которыми пользовались греки.

У Диофанта впервые появляется буквенная символика. Он ввел обозначения: неизвестной z, квадрата d), куба c, четвертой ddВа(квадратоквадрат), пятой dcВа(квадратокуб) и шестой степеней ее, а также первых шести отрицательных степеней, т. е. рассматривал, величины, записываемые нами в виде x⁶, x⁵, x⁴, x³, x², x, x^-1, x^-2, x^-3, x^-4, x^-5, x^-6. Диофант применял знак равенства (символ i) и знак 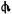Вадля обозначения вычитания.

Диофант сформулировал правила алгебраических опeраций со степенями неизвестной, соответствующие нашим умножению и делению степеней с натуральными показателями (для m + n 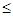Ва6), и правила знаков при умножении. Это дало возможность компактно записывать многочлены, производить умножение их, оперировать с уравнениями. Он указал также правила переноса отрицательных членов уравнения в другую часть его с обратными заиками, взаимного уничтожения одинаковых членов в обеих частях уравнения.

ВлАрифметикаВ» посвящена проблеме решения неопределенных уравнений. И хотя Диофант считает число собранием (а это означает, что рассматриваются только натуральные числа), при решении неопределенных уравнений он не ограничивается натуральными числами, а отыскивает и положительные рациональные решения.

Неопределенными уравнениями до Диофанта занимались математики школы Пифагора в связи с пифагоровой теоремой. Они искали тройки целых положительных чисел, удовлетворяющих уравнению x² + y² = z².

Диофант поставил задачу установить разрешимость (в рациональных числах) и в случае разрешимости найти рациональные решения уравнения F (х, у) = 0, где левая часть тАУ многочлен с целыми или рациональными коэффициентами. Он исследовал неопределенные уравнения второй, третьей и четвертой степеней и системы неопределенных уравнений.

Во второй книге ВлАрифметикиВ» он так исследует, например, уравнение второго порядка F (х, у) = 0.

Это уравнение задает коническое сечение. Всякому рациональному решению уравнения соответствует точка кривой с рациональными координатами. Пусть a, b тАУ такие координаты, т. е. F (a, b) = 0.

Диофант делает подстановку у = b + k (х тАУ а), или y = b + kt, х = а + t.

Тогда F (а + t, b + kt) = F (a, b) + tA (а, b) + ktB (а, b) + t²C (a, b, k) = 0.

Но F (a, b) = 0, поэтому t = тАУ.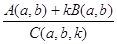

Это означает, что каждому рациональному значению параметра k соответствует рациональное же значение t, а значит, рациональная точка кривой. Очевиден геометрический смысл решения: через рациональную точку кривой (a, b) проводится прямая y тАУ b =k (x тАУ a) и находятся вторая точка ее пересечения с кривой.

ВаМетоды Диофанта впоследствии применяли и развивали арабские ученые, Виет (1540тАФ1603), Ферма, Эйлер (1707тАФ1783), Якоби (1804тАФ1851), Пуанкаре (1854тАФ1912).

Оценивая творчество Диофанта, Цейтен отмечает существенную деталь: ВлНаконец, мы желаем здесь вкратце указать на важную роль, сыгранную впоследствии сочинениями Диофанта. Благодаря тому, что определенные уравнения первой и второй степени были облечены у него в численную оболочку они оказались гораздо более доступными для людей, не посвященных еще в культуру греческой математики; более доступными, чем те абстрактные геометрические формы, которые принимают у Евклида уравнения второй степени и которые мы встречаем в сохранившихся до нас трудах других геометров для выражения уравнений первых двух степеней. Поэтому Диофант и явился главным посредником в процессе усвоения греческой алгебры арабами, благодаря которым, в свою очередь она проникла в Европу в эпоху возрождения наукВ».

2.1.3 Алгебра индусов.

Начиная с V в. центр математической культуры переместился на восток - к индусам и арабам. Математика индусов резко отличалась от математики греков она была числовой. Индусы не были озабочены строгостью эллинов в доказательствах и обосновании геометрии. Они довольствовались чертежами, на которых у греков основывалось доказательство, сопровождая их указанием: ВлСмотри!В». Предполагается, что благодаря числовым выкладкам и практическому эмпиризму индусам удалось постичь теоремы и методы греков, теоретического обоснования которых они, возможно, по-настоящему не понимали.

Основные достижения индусов состоят в том, что они ввели в обращение цифры, называемые нами арабскими, и позиционную систему записи чисел, обнаружили двойственность корней квадратного уравнения, двузначность квадратного корня и ввели отрицательные числа.

Индусы рассматривали числа безотносительно к геометрии. В этом их алгебра имеет сходство с алгеброй Диофанта. Они распространили правила действия над рациональными числами на числа иррациональные, производя над ними непосредственные выкладки, а не прибегая к построениям, как это делали греки. Например, им было известно, что

Греки, не знавшие отрицательных чисел, решая уравнения, преобразовывали их так, чтобы обе части уравнения при значении неизвестной, удовлетворяющей этому уравнению, были положительными. Если этого не происходило, то менялись условия задачи. Индусы в аналогичных ситуациях не были стеснены в своих действиях: они либо отбрасывали получающиеся отрицательные решения, либо интерпретировали их как долг, задолженность. Отсюда сделан был естественный шаг к установлению правил действий над величинами при любом выборе знаков этих величин, а также к выявлению наличия двух корней у квадратных уравнений и двузначности квадратного корня.

Индусами был сделан шаг вперед по сравнению с Диофантом и в совершенствовании алгебраической символики: они ввели обозначения нескольких различных неизвестных и их степеней, которые были, как у Диофанта, по сути дела сокращениями слов. Кроме того, они искали решения неопределенных уравнений не в рациональных, а в целых числах.

2.1.4 Алгебра арабов.

Дальнейшее развитие математика получила у арабов, завоевавших в VII в. Переднюю Азию, Северную Африку и Испанию. Создались благоприятные условия для слияния двух культур тАУ восточной и западной, для усвоения арабами богатого математического наследия эллинов и индусской арифметики и алгебры.

Но еще до того как началось усиленное изучение арабами трудов древних математиков, в 820 г., вышел трактат по алгебре ВлКраткая книга об исчислении ал-джабра и ал-мукабалыВ» Мухаммеда ибн Муса ал-Хорезми (т. е. из Хорезма, 787 тАУ ок. 850г. н. э.), где давались числовое и геометрическое решения уравнений первой и второй степеней.

ВаНазвание трактата соответствует операциям при решении уравнений: Влал-джабрВ» (восстанавливать) означает восстановление отрицательного члена в одной части уравнения в виде положительного в другой. Например, преобразовав уравнение

2х² + Зх -2 = 2х к виду 2х² + Зх = 2х + 2, мы произвели операцию ал-джабр.

ВаВлАл-мукабалаВ» означает сопоставление подобных членов, приведение их к одному; в нашем уравнении подобные члены Зх и 2х, поэтому получим 2x² + x = 2.

Модификация слова ал-джабр породила более позднее алгебра. Аналогично, слово алгорифм (алгоритм) произошло от ал-Хорезми.

Основное внимание в трактате ал-Хорезми обращает на решение уравнений вида

ax² = bx, ax² = c, ax² + bx = c, ax² + c = bx, bx + c = ax², bx = c,

которые формулирует словесно, например, так: Влквадраты и корни равны числуВ» (ах² + bх = с). Он высказывает правила, дающие только положительные решения уравнений, определяет условия, при которых эти решения существуют. Обоснование правил ал-Хорезми дает в духе геометрической алгебры древних.

От арабов Европа получила следующий способ решения уравнения

х² + ах = b.

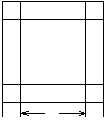
Построим квадрат х², к его сторонам приложим четырехугольники длины х + 2а/4 = х + а/2 и ширины а/4. Тогда площадь полученного квадрата 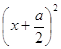= x² + ax + .

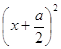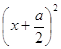Значит, x² + ax + Ва= = b + , = b + .

Величины b и а известны, поэтому можно построить 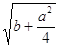, откуда х + 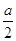= 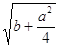-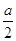. Впрочем, ал-Хорезми, приведший в своем сочинении этот метод, уравнению ах² + с = bх приписывал два корня.

В трактате приведены некоторые сведения о действиях над алгебраическими выражениями, примеры решения треугольников много задач о разделе наследства приводящих к уравнениям первой степени. Таким образом, трактат ал-Хорезми не содержал ничего нового по сравнению с тем, что было у греческих авторов и индусов, но он заслуживает внимания потому, что в течение длительного времени был руководством, по которому велось обучение в Европе.

2.1.5 Развитие алгебры в Европе.

Каково же было состояние математики в это время в Европе. Об этом наука располагает крайне скудными сведениями.

В XII тАУ XIII вв. в Европе интенсивно переводились в арабского языка как труды самих арабов, так и работы древних греков, переведенные на арабский язык.

Первым европейским математиком, которому удалось осветить многие вопросы и внести в математику свой вклад, был Леонардо Пизанский (Фибоначчи, 1180тАУ1240), написавший ВлКнигу абакаВ». В ней рассмотрены различные задачи, указаны методы их решения, причем арифметика и алгебра линейных и квадратных уравнений изложены с небывалой до этого времени точностью и полнотой.

Существо задачи Леонардо излагает словесно; неизвестную он называет res (вещь) или radix (корень); квадрат неизвестной тАУ census (имущество) или quadratus (квадрат); данное число тАУ numerus. Все это латинские пероводы соответствующих латинских слов.

Современник Леонардо, Иордан Неморарий (XIII в), употреблял буквенные обозначения более систематично и решал задачи с применением линейных и квадратных уравнений, сначала в общем виде, а затем иллюстрировал их числовыми примерами.

Французский епископ Николь Орем (1323-1382) рассматривал Влдробно тАУ рациональные отношенияВ», соответствующе современным степеням a^½, a^¼, a^3/2 и т.д., сформулировал правила операций с этими отношениями типа 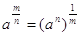,ВаВаВа ,ВаВаВаВаВаВаВаВа 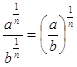,ВаВаВаВаВаВаВаВаВаВаВаВаВаВа 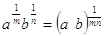,ВаВаВаВаВаВаВаВаВаВаВа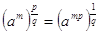

Орем вплотную подошел к понятию иррационального показателя. Он доказал расходимость гармонического ряда 1 + 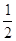++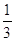+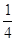тАж

Выдающимся алгебраистом своего времени стал монах-францисканец Лука Пачоли (ок. 1445 тАУ ок.1514) близкий друг Леонардо да Винчи, работавший профессором Математики в университетах и различных учебных заведениях Рима, Болоньи, Неаполя, Флоренции, Милана и других городов.

Он ввел Влалгебраические буквыВ» (caratteri algebraici), дал обозначения квадратному и кубическому корням, корню четвертой степени; неизвестную х он обозначал со (cosa тАУ вещь), х² тАУ се (censo - квадрат, от латинского census), х³ тАУ cu (cubo), x⁴ тАУ се. се. (censo de censo), x⁵ тАУ рВ°гВ° (primo relato тАУ Влпервое relatoВ», x⁶ тАУ рВ°гВ° х тАУ се. cu. (censo de Влвторое relatoВ»), х⁸ тАУ ce. ce. ce. (de censo), x⁹ тАУ cu. cu. (cubo de cubo), x¹⁰ тАУ ce. pВ°rВ° (censo de primo relato), x¹³ тАУ 3В°rВ° (tersio relato - Влтретье relatoВ») и т. д.; свободный член уравнения тАУ nВ° (numero тАУ число). Как видим, некоторые степени Пачоли получал мультипликативным способом с помощью показателей 2 и 3 (х⁴ = х^2×2 , х⁶ = х^2×3, х⁹ = х^3×3 и т. д.), а в случаях, когда так не получалось, пользовался словом relato (например, при образовании х⁵, х⁷, х¹¹ и т. д.). Специальными символами Пачоли обозначил вторую неизвестную и ее степени. Для обозначения операции сложения он воспользовался знаком 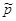Ва(plus тАУ больше), для обозначения вычитания тАУ знаком 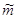Ва(minus тАУ меньше). Он сформулировал правила умножения чисел, перед которыми стоят знак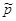и и .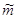

Раздел ВлСуммыВ», посвященный алгебраическим уравнениям, Пачоли закончил замечанием о том, что для решения кубических уравнений х³ + ах = b и х³ + b = ах Влискусство алгебры еще не дало способа, как не дан еще способ квадратуры кругаВ».

Некоторый шаг в совершенствовании алгебраической символики сделал бакалавр медицины Н. Шюке (ум. ок. 1500 г.), который в книге ВлНаука о числах в трех частяхВ» изложил правила действий с рациональными и иррациональными числами и теорию уравнений. Для сложения и вычитания он вслед за Пачоли пользовался знакам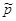и Ваи 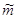, причем, знак 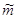Васлужил и для обозначения отрицательного числа. Неизвестную величину он называл premier (Влпервое числоВ»), а ее степени тАУ вторыми, третьими и т. д, числами. Записи степеней неизвестной у Шюке лаконичны. Например, современные символы 5, 5ж, 5х, 5х², 5х³ у него выглядели бы так: 5В°, 5¹, 5², 5³. Вместо равенства 8х³×7х^-1 = 56х² Шюке писал: Вл8³, умноженное на 7^1×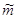, дает 56²В». Таким образом, он рассматривал и отрицательные показатели. Относительно свободных членов уравнения Шюке указывал, что эти числа Влимеют имя нульВ».

Значительного успеха в совершенствовании Влалгебраических буквВ» Луки Пачоли достигли немецкие алгебраисты тАУ ВлкоссистыВ». Они вместо 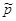Ваи 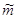ввели знаки + и тАУ, знаки для неизвестной, и ее степеней, свободного члена.

XVI в. в алгебре ознаменовался величайшим открытием тАУ решением в общем виде уравнений третьей и четвертой степеней.

Спицион дель Ферро в 1506 г. нашел решение кубического уравнения вида

Ваx³ + ax = b a,b >0. (1)

Чуть позже Тарталья указал решение этого же уравнения в виде х = 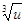- 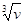, где u тАУ v = b, uv = , откуда u и v находятся как корни квадратного уравнения.

Также он нашел решение уравнения x³ = ax + b a,b >0 (2)

в виде х = 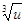+ 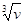, где u + v = b, uv = .

Уравнение же x³ + b = ax a,b >0 можно ре

Вместе с этим смотрят:

"Инкарнация" кватернионов

* Алгебры и их применение

*-Алгебры и их применение

10 способов решения квадратных уравнений

Bilet