Системы уравнений межотраслевого баланса
Лабораторную работу выполнил Сиропов Вадим Александрович
Южно-Российский государственный университет экономики и сервиса
Цели:
Выработать у студентов навыки построения математических моделей межотраслевого баланса в статистических случаях и оптимизации моделей в рамках межотраслевого баланса. Научиться делать выводы в рамках построения моделей.
Задание:
Найти объемы выпуска продукции по каждой из отраслей, предварительно обосновав сущность нестандартного решения.
Рассчитать новый план выпуска продукции, при условии, что конечный спрос на продукцию U-ой и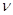 
-ой отраслей возрос соответственно на 85 и 97 единиц. Вычислить абсолютные и относительные приросты объема, выполненные по каждой из отраслей.
Скорректировать новый план, с учетом того, что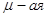 
Ваотрасль не может увеличить объемы выпуска своей продукции более чем на 2 единицы.
Рассчитать матрицу полных затрат.
Исходные данные:
  A =
| 0.02 0.01 0.01 0.05 0.06 | 0.03 0.05 0.02 0.01 0.01 | 0.09 0.06 0.04 0.08 0.05 | 0.06 0.06 0.05 0.04 0.05 | 0.06 0.04 0.08 0.03 0.05 | | C = | 235 194 167 209 208 | |
| | | | | | | | | |
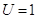, ВаВа 
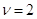,ВаВаВаВаВаВаВаВаВаВаВаВа 
.
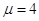0) Проверим матрицу А на продуктивность:
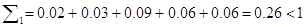
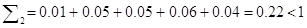
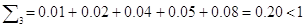
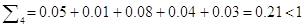
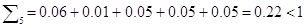
Матрица А является продуктивной матрицей.
(J-A)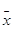
Ва=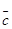 
J тАУ единичная матрица;
A тАУ заданная матрица прямых затрат;
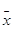Ва- вектор (план) выпуска продукции, подлежащей определению;
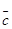Ва- вектор конечного спроса.
Произведем расчеты на PС, используя метод Гаусса.
Ва; ВаВаВаВаВаВаВаВаВа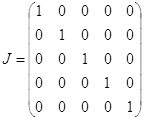 
;
;
;
;
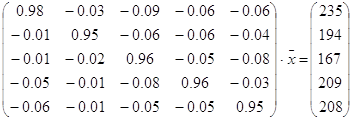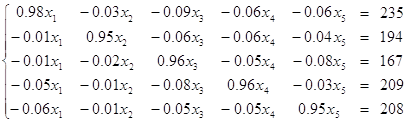Используя Симплекс-метод, получим:
