Сравнения высших степеней

Вступ

Важливе мiсце в курсi теорii чисел посiдають конгруенцii та, зокрема, конгруенцii вищих степенiв. Але до того як вони почали розглядатися, математики рiзних краiн, протягом столiть розглядали невизначенi рiвняння 1-го степеня.

Невизначенi рiвняння 1-го степеня почали розглядатися ще iндуськими математикамиВа приблизно з V столiття. Деякi такi рiвняння з двома i трьома невiдомими з'явилися в зв'язку з проблемами, що виникли в астрономii, наприклад, при розглядi питань, зв'язаних з визначенням перiодичного повторення небесних явищ.

У другому виданнi книги французького математика Баше де МезiртАЩяка тАЬProblemis plaisans et delectables que se font par les nombresтАЭ, що вийшли в 1624 р., зважуiться невизначене рiвняння ax+by=c. Баше де МезiртАЩяк фактично застосовуi процес, що зводить до послiдовного обчислення не повних часток i розгляду придатних дробiв; однак вiн не розглядав неперервних дробiв як таких. Популярний твiр Баше де МезiртАЩяка дуже вплинув на розвиток теорii чисел, так як сприяв виникненню iнтересу до цiii областi математики.

Ланцюговi дроби до рiшення таких рiвнянь були застосованi Лагранжем, котрий, однак, зауважуi, що фактично це той же спосiб, що був даний Баше де МезiртАЩяком i iншими математиками, що розглядали невизначенi рiвняння до нього.

Невизначенi рiвняння 1-го степеня стали записуватися й розв'язуватися у формi порiвняння значно пiзнiше, починаючи з Гауса. Вiн вперше систематизував теорiю та визначив поняття конгруенцii, в своiй книзi тАЬDisquisitiones arithmeticaeтАЭ (тАЬДослiдження з арифметикитАЭ).

Задачi, що зводяться до розгляду системи порiвнянь 1-го степеня, розглядалися в арифметицi китайськогоВа математика Сун Тзу, що жив приблизно на початку нашоi ери. У нього як у цiлого ряду китайських, iндуських, арабських i iвропейських учених, що вирiшували такi задачi пiсля нього, питання ставився в наступнiй формi: знайти число, що даi заданi остачi вiд дiлення на заданi числа. Робота Сун Тзу стала вiдомою в РДвропi в 1852 р. Незалежно вiд китайських математикiв спосiб рiшення задач такого роду був даний iндуським математиком Брамегупта (588-660).

Система n порiвнянь iз n невiдомими вивчалася Гаусом. Повне дослiдження систем лiнiйних конгруенцiй було подано в роботах Фробенiуса й Стейнiца наприкiнцi XIX столiття.

РЖ так конгруенцii вищих степенiвВа були покладенi в основу модулярного представлення числа, яке широко використовуiться в сучаснiй криптографii, що досить актуальна в наш час високих технологiй. Велику увагу цьому питанню придiлили такi вченi-дослiдники як Рiверс, Адельман та Ширман.

1. Конгруенцii i класи

Ряд чисел при дiленнi на одне i те саме число дають одну i ту ж саму остачу. Постаi питання про те, як можна використати цю особливiсть i якi властивостi вона маi. Вiдповiдь на нього тАУ конгруенцii.

1.1. Конгруенцii та iх основнi властивостi

Припустимо, що m i натуральне число; розглядатимемо цiлi числа в зв'язку з остачами вiд дiлення iх на дане натуральне т, яке називають модулем. Згiдно з теоремою про дiлення з остачею кожному числу а вiдповiдатиме певна остача r вiд дiлення а на r :

a=mq+r, 0 ≤ r < m.

Якщо двом цiлим числам a i b вiдповiдаi одна i та сама остача r вiд дiлення iх на m, то вони називаються конгруентними за модулем m. Це позначаiться символом:

a≡b(mod m)ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)

i читаiться: а конгруентне з b за модулем m.

Деякi автори позначають це коротше:

a≡b(m).ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1′)

Спiввiдношення (1) або (1′) мiж числами називаються порiвнянням, або конгруенцiiю.

Приклади. 48 ≡ 84 (mod 18);

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 131 ≡ 1 (mod 13);

ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа 10 ≡ тАУ1 (mod 11).

Конгруенцii мають багато властивостей, подiбних до властивостей рiвностей.

Властивiсть 1.ВаВа ДляВаВа конгруенцiйВаВа справджуютьсяВа триВа основнi закони рiвностей:Ва рефлексивностi,Ва симетрii i транзитивностi, тобто вiдповiдно:

а)Ва a≡a(mod m),

б) з конгруенцii a≡b(mod m) випливаi, що b≡a(mod m);

в) якщо a≡b(mod m) i b≡c(mod m), то a≡c(mod m).

Властивiсть 2. Конгруенцii за одним i тим же модулем можна почленно додавати (або вiднiмати).

Висновок 1. Доданок, що стоiть в якiй-небудь частинi конгруенцii, можна переносити в iншу частину, змiнивши знак на протилежний.

Висновок 2. Можна додати до обох частин або вiдняти вiд обох частин конгруенцii одне i те саме число.

Висновок 3. До кожноi частини конгруенцii можна додати (або вiдняти вiд неi) довiльне число, кратне модулевi.

Властивiсть 3. КонгруенцiiВа за одним i тим самим модулем можна почленно перемножувати.

Висновок 1. Обидвi частини конгруенцii можна помножити на одне й те саме цiле число.

Висновок 2. Обидвi частини конгруенцii можна пiдносити до одного i того самого цiлого невiд'iмного степеня, тобто, якщо a≡b(mod m), то aⁿ≡bⁿ(mod m), де n тАФ цiле ≥0.

Властивiсть 4. Обидвi чистини конгруенцii можна подiлити на iх спiльний дiльник, якщо вiн i взаiмно простий з модулем.

Властивiсть 5. Обидвi частини конгруенцii i модуль можна помножити на одне i те саме натуральне число.

Властивiсть 6. Обидвi частини конгруенцii i модуль можна подiлити на будь-якого iх спiльного дiльника.

Властивiсть 7. Якщо конгруенцiяВа маi мiсце за кiлькома модулями, то вона матиме мiсце i за модулем, що дорiвнюi iх найменшому спiльному кратному.

Властивiсть 8. Якщо конгруенцiя маi мiсце за модулем тАУm, то вона матиме мiсце i за будь-яким дiльником d цього модуля.

Властивiсть 9. Якщо одна частина конгруенцii i модуль дiляться на яке-небудь цiле число, то i друга частина конгруенцii маi дiлитись на це число.

Властивiсть 10. Числа а i b, конгруентнi мiж собою за модулем т, мають з ним одного i того самого найбiльшого спiльного дiльника.

1.2. Класи за даним модулем

Вiзьмемо деяке натуральне число т; при дiленнi на т, будь-якихВа цiлихВа чиселВа можнаВа дiстати тiльки т рiзнихВа невiд'iмних остач, а саме: 0, 1,2, .. , т-1. Отже, множина всiх цiлих чисел розiб'iться на т класiв чисел, що не перетинаються; при цьому числа, якi при дiленнi на т, даватимуть одну i ту саму остачу r (0 ≤ r < т), тобто числа, конгруентнi за модулем т, утворюють клас чисел за модулем т.

РЖз сказаного випливаi, що всiм числам даного класу вiдповiдаiВа одна i та самаВа остача r; отже,ВаВа дiстанемоВа всiВа числаВа цього класу, якщо в формi mq+r, де r тАФ стале, припустимо, що q набираi значення всiх цiлих чисел.

З означенняВа конгруентностiВаВа двохВа чисел а i b за модулем т iз щойно сказаного вiдразу ж випливаi таке твердження.

Два цiлих числа а i b тодi i тiльки тодi належать до одного класу за модулем т, коли вони конгруентнi за цим модулем.

Позначимо через C₀ клас чисел, якi дiляться на т; через C₁тАФ клас чисел, якi при дiленнi на т дають в остачi 1, i т. д. i нарештi, через C_m-1 тАФ клас чисел, якiВа при дiленнiВа на т дають в остачi т-1.

Будь-яке число даного класу називаiться лишком,Ва або представником цього класу. Отже, якщо число a iВа представником деякого класу за модулем т, то будь-яке iнше число b цього класу задовольняi умову:ВаВаВа b≡a(mod m), або b=а + тt,Ва де t тАФ деяке цiле число, тобто, iнакше кажучи, b = а + тt i загальний вигляд цiлих чисел, якi належать до того самого класу, що й а.

2.
Конгруенцii з невiдомою величиною

Як видно з наведеного нижче малюнку, конгруенцii в теорii чисел подiляються на конгруенцii за простим та за складеним модулями.

Види конгруенцiй Рисунок

2.1. Класи розв'язкiвВа конгруенцii довiльного степеня

Припустимо,Ва щоВа т тАФ натуральне число. Конгруенцiя виду

f (x) ≡ 0(mod m),ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)

де f (х)= а₀х^п + а₁х^п-1 + . . . + а_n-1x + a_n, i многочлен степеня n з цiлими коефiцiiнтами i а₀ ≠ 0 (mod m) називаiться алгебраiчною конгруенцiiю п-го степеня з одним невiдомим x.

Цiлi значення х, що задовольняють конгруенцiю (1), називаються коренями або розв'язками цiii конгруенцii.

Розв'язати конгруенцiю тАФ це означаi знайти всi значення невiдомих, якi ii задовольняють.

Двi конгруенцii з одним невiдомим називаються еквiвалентними, якщо всякий розв'язокВа однiiiВаВа конгруенцiiВа iВа розвтАЩязком iншоi.

Теорема 1. Якщо x = x₁ задовольняi конгруенцiю (1), то всяке число, яке належить до того самого класу лишкiв за модулем т , що й число x₁, також задовольняi цю конгруенцiю, тобто розв'язком буде весь клас чисел

х ≡ х₁(mod т).

Це твердження безпосередньо випливаi з властивостей конгруенцiй. Справдi, нехай х₂ тАФ будь-яке число, яке належить до того самого класу лишкiв за модулем т, що й х₁; тодi х₂ ≡ x₁(mod m). За умовою х₁ i розв'язок конгруенцii (1), тобто маi мiсце тотожна конгруенцiя f(x₁) ≡ 0 (mod т), але тодi матиме мiсце й конгруенцiя f(x₁) ≡ 0 (mod т), тобто x₂ також буде розв'язком конгруенцii. Оскiльки x₂ тАФ будь-яке число класу х ≡ х₁(mod т), то весь цей клас задовольнятиме дану конгруенцiю.

Розв'язки конгруенцii (1), що належать до одного класу чисел за модулем т, приймають за один розв'язок даноi конгруенцii. При цьому конгруенцiя (1) маi стiльки розв'язкiв, скiльки класiв чисел ii задовольняють.

Приклад. Конгруенцiя

8x⁵ тАФ 12x³ тАФ 13x² тАФ 15x + 6 ≡ 0 (mod 5)

i еквiвалентною конгруенцii

Зх⁵ тАФ 2x³ тАФ Зx² +1 ≡ 0 (mod 5),

або конгруенцii

Зх⁵ + 3x³ + 2x² +1 ≡ 0 (mod 5).

Щоб знайти розв'язки останньоi конгруенцii, випробуiмо, приклад, абсолютно найменшi лишки за модулем 5:Ва 0, 1, 2, -2, -1. Безпосередньо видно, що 0, 1, -1 задану конгруенцiю не задовольняють. При дальшому випробуваннi можна скористатись схемою Горнера ( Див. Додаток) з тiiю тiльки вiдмiннiстю, що для полегшення кожного разу можна вiдкидати числа, кратнi модулю.

	3	0	3	2	0	1
2	3	6≡1	5≡0	2	4	9≡4
-2	3	6≡ -1	5≡0	2	-4	9≡4

Отже,ВаВа конгруенцiя Зх⁵ + 3x³ + 2x² +1 ≡ 0 (mod 5) не маi розв'язкiв, а тому не маi розв'язкiв i конгруенцiя

8x⁵ тАФ 12x³ тАФ 13x² тАФ 15x + 6 ≡ 0 (mod 5).

При розв'язуваннi конгруенцii з невiдомою величиною iнодi доводиться множити обидвi частини конгруенцii на цiле число. Для тотожних конгруенцiй ця операцiя, як ранiш було показано, завжди законна. Для конгруенцiй з невiдомою величиною таке перетворення не завжди законне, тобто, iнакше кажучи, при такому перетвореннi конгруенцii може порушитись еквiвалентнiсть даноi i добутоi конгруенцiй.

Приклад. Конгруенцiя

x⁴ + х³ + х² + х + 1 ≡ 0 (mod 5),

як ми вище бачили, маi один розв'язок: x ≡ 1 (mod 5). Але, якщо обидвi частини цiii конгруенцii помножити на 5, то дiстанемо конгруенцiю:

5x⁴ + 5х³ + 5х² + 5х + 5 ≡ 0 (mod 5),

розв'язком якоi буде вже будь-яке цiле число. Вона, по сутi, перетворюiться в конгруенцiю 0 ≡ 0 (mod 5).

Конгруенцii виду 0 ≡ 0 (mod 5) мають очевидно розв'язком будь-яке цiле значення невiдомого х, тобто i тотожною конгруенцiiю.

Пiсля наведеного щойно прикладу виникаi питання, коли множення обох частин конгруенцii з невiдомою величиною на цiле число i законним? Вiдповiдь на це даi теорема 2.

Теорема 2. Якщо обидвi частиниВа конгруенцii (1) помножити на цiле число k, взаiмно просте з модулем т, то дiстанемо конгруенцiю, еквiвалентну данiй.

Справдi, припустимо, що

х = α (mod т)

i який-небудь розв'язок конгруенцii (1), тодi

f (α) ≡ 0 (mod m).

ПомножаючиВа обидвiВа частиниВа цiiiВа конгруенцiiВа на k,ВаВа дiстанемо:

k∙f (α) ≡ 0 (mod m).ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)

Отже, ми бачимо, що α i розв'язком конгруенцii

k∙f (x) ≡ 0 (mod m).ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)

Навпаки, якщо α тАФ розв'язок конгруенцii (3), тобто k∙f (α) ≡ 0 (mod m), тодi обидвi частини конгруенцii (2) можна скоротити на k, не змiнюючиВа модуля,Ва бо (k,Ва m) = 1,ВаВа (див.Ва властивiсть 4, п.1.1), отже,

f (α) ≡ 0 (mod m),

тобто α i розв'язком конгруенцii (1), що i доводить наше твердження.

Зауважимо, що при розв'язуваннi конгруенцiй з невiдомою величиною можна, не змiнюючи модуля, скорочувати обидвi частини конгруенцii тiльки на такий iх спiльний дiльник, який i взаiмно простий з модулем (див. властивiсть 4, п.1.1).

2.2. Конгруенцii
-го степеня за простим модулем.

У попередньому параграфi ми бачили, що дослiдження й розв'язання конгруенцii п-го степеня (п≥1) зводиться кiнець кiнцем до дослiдження i розв'язання вiдповiдних конгруенцiй за простими модулями. Тому зараз доведемо деякi загальнi теореми, що стосуються конгруенцiй n-го степеня за простим модулем р.

Припустимо, що задано конгруенцiю[1]
:

f (х)= а₀х^п + а₁х^п-1 + . . . + а_n-1x + a_n ≡ 0 (mod p), n≥1,ВаВаВаВаВаВаВаВаВаВа (1)

де a₀≠0 (mod p) i р тАФ просте число.

Теорема 1. Конгруенцiю (1) завжди можна так перетворити що ii старший коефiцiiнт дорiвнюватиме одиницi.

Справдi, через те що р тАФ просте i a₀ не дiлиться на р, то завжди iснуi iдине число α, що а₀α ≡ 1 (mod p). Помноживши тепер конгруенцiю (1) на α i замiнивши а₀x одиницею, дiстанемо еквiвалентнуВаВа конгруенцiю з старшим коефiцiiнтом, що дорiвнюi одиницi:

xⁿ + b₁x^n-1+ . + b_n-1x + b_n≡ 0 (mod p);ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1')

тут b_i ≡ a_iα (mod p).

Теорема 2. Якщо степiнь конгруенцii (1) не менший вiд модуля конгруенцii, то вона еквiвалентна деякiй конгруенцii степеня, не вище за ртАФ1 (за тим самим модулем).

Справдi, подiлимо f(х) на х^р-х; i частку вiд дiлення позначимо через q(x), а остачу через r(х). Тодi на пiдставi алгоритму дiлення з остачею дiстанемо:

f(x) = (x^pтАФx)q(x) + r(x),

де частка q(х) i остача r(х) будуть многочленами з цiлими коефiцiiнтами, причому степiнь r(х) буде не вище ртАФ1. За теоремою Ферма x^pтАФ-x ≡ 0 (mod p) при будь-якому цiлому х, тому дiстанемо тотожну конгруенцiю:

f(х) ≡ r(x) (mod р).

Ця тотожна конгруенцiя показуi, що коренi конгруенцii (1) i конгруенцiiВаВа r(х)≡0 (mod р) однаковi. Оскiльки х^р тАФ х завжди дiлиться на p, то f(x) i r(x) можуть дiлитись на p тiльки одночасно; отже, конгруенцii

f(х) ≡ 0 (mod р) i r(х) ≡ 0 (mod р)

еквiвалентнi. Через те що степiнь r(x) менше за p, то теорему доведено.

Зокрема, може статись, що f(x) дiлиться на x^pтАФ-x , тобто r(х) ≡ 0 (mod р) тАУ тотожна конгруенцiя за модулем p, тобто остача при дiленнi конгруентна з нулем i дана конгруенцiя еквiвалентна конгруенцii 0 ≡ 0 (mod p) та справедлива при будь-якому цiлому x. Далi, нехай остача вiд дiлення f(х) на x^pтАФ-x i многочлен нульового степеня, що дорiвнюi b_p-1. Якщо b_p-1 не дiлиться на p, то дана конгруенцiя не маi розвтАЩязкiв, бо вона зводиться до невiрноi конгруенцii :

b_p-1 ≡ 0 (mod p).

Приклад. Якiй конгруенцii нижче вiд 5-го степеня еквiвалентна конгруенцiя:

f(х) = х¹⁷ + 2x¹¹ + Зx⁸ тАФ 4x⁷ + 2x тАФ 3 ≡ 0 (mod 5).

Подiливши f (х) на х⁵ тАФ х i замiнивши всi коефiцiiнти остачi найменшими невiд'iмними лишками за модулем 5, дiстанемо, що дана конгруенцiя еквiвалентна конгруенцii

r(х) = Зx⁴ + Зx³ + Зx + 2 ≡ 0 (mod 5).

Зауваження. Можна вказане дiлення на х^p тАФ х фактично i не виконувати, а просто замiнити хⁿ на х^r, де r > 0 i остача вiд дiлення п на р тАФ 1. Справдi, за теоремою Ферма х^р ≡ х (mod р), звiдси x^p+1 ≡ x², x^p+2 ≡ x³, .. i взагалi:

Через те що в нашому прикладi x¹⁷ можна замiнити через х, а 2x¹¹ через 2x³,Ва Зx^8ВаВа через Зx⁴,тАФ4x⁷ замiнити через тАФ4x³ ≡ x³ , тому вiдразу дiстанемо:

f(x) ≡ Зx⁴ + Зx³ + Зx + 2 ≡ 0 (mod 5).

У свою чергу, останню конгруенцiю можнаВа спростити так: х ≠ 0 (mod 5), тому x^5-1 ≡ 1 (mod 5) i

f(x) ≡ Зх³ + Зх ≡ 0 (mod 5),

або

f(x) ≡ х² + 1 ≡ 0 (mod 5).

Очевиднi розв'язки останньоi конгруенцii x ≡ 2, 3 (mod 5) будуть також i розв'язками даноi конгруенцii:

f(x) ≡ 0 (mod 5).

Теорема 3. Якщо α₁тАФякий-небудьВаВа розв'язокВаВа конгруенцiiВаВа (1), то маi мiсце тотожна конгруенцiя:

f (х) ≡ (х тАФ α₁) f₁ (х) (mod р),ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)

де f₁(х) тАФ многочлен степеня, на одиницю нижчий вiд степеня многочлена f(x). Старший коефiцiiнт многочлена f₁(x) збiгаiться з старшим коефiцiiнтом даного многочлена fix).

Справдi, подiлимо f(x) на х тАФ α₁ВаВа iВаВа часткуВаВа позначимоВаВа через f₁(х), а остачу через r. За теоремою Безу r = f(α₁), але

f(α₁) ≡ 0 (mod p)

за умовою, тодi конгруенцiю

f(x) = (x тАУ α₁) f₁(x) + f(α₁) ≡ 0 (mod р)

можна переписати так:

f(x) ≡ (x-α₁)f₁(x) (mod p).

При цьому кажуть, що f(х) дiлиться на х тАФ α₁ за модулем р. Очевидно, що й навпаки: з конгруенцii (2) випливаi, що f(α₁) ≡ 0 (mod p) тобто α₁ тАФ корiнь конгруенцii (1); отже, маiмо такий висновок.

Висновок. Конгруенцiя (1) маi корiнь х = α₁ тодi i тiльки тодi, коли лiва ii частина f(x) дiлиться на х тАФ α₁ за даним модулем р.

Зауважимо, що теорема 3 i висновок з неi справедливi i для складеного модуля т.

Теорема 4. Якщо α₁, α₂, . . , α_k (k ≤ n) i рiзнi розв'язки конгруенцii (1), то маi мiсце тотожна конгруенцiя:

f (х) ≡ (х тАУ α₁) (х - α₂) . . . (х - α_k) f_k (x)Ва (mod p),ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)

де степiнь f (х) дорiвнюi п тАФ k i старшi коефiцiiнти у f(x) i f_k(x) однаковi.

Справдi, згiдно, з теоремою 3 конгруенцiя (1) еквiвалентна конгруенцii

(x - α₁)f₁(x) ≡ 0 (mod p).ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2¹)

Через те що α₂ i розв'язок конгруенцii (1), то, пiдставляючи його в еквiвалентну конгруенцiю (2'), дiстанемо тотожну конгруенцiю:

(α₂ тАФ α₁)f₁(α₂) ≡ 0 (mod р).

Але добуток двох чи кiлькох чисел дiлиться на просте число р тодi i тiльки тодi, коли на р дiлиться принаймнi один з спiвмножникiв. За умовою α₁ i α₂ рiзнi, тобто

α₁≠α₂ (mod p),

отже, α₂ тАФ α₁ не дiлиться на р, а тому f₁(α₂) дiлиться на р, тобтоВаВаВа f₁(α₂) ≡ 0 (mod p); останнi означаi, що α₂ тАФ розв'язок конгруенцii f₁(x)≡0 (mod p). За теоремою 3 дiстанемо:

f₁(х)≡ (x-α₂)f ₂(x) (mod p);

звiдки

f(x)≡(x-α₁)(x-α₂)f₂(x) (mod p).

Аналогiчно мiркуючи, кiнець кiнцем прийдемо до тотожноi конгруенцii (3). З самого процесу одержання многочленiв f₁(x), f₂(x),тАж f_k (x) видно, що старшi коефiцiiнти цих многочленiв однаковi i дорiвнюють старшому коефiцiiнтовi a₀ многочлена f(x).

В и с н о в о к. Якщо конгруенцiя (1) п-го степеня за простим модулем р (п можна вважати не бiльшим за р тАФ 1) маi п рiзних розв'язкiв α₁, α₂, . . , α_n, то маi мiсце тотожна конгруенцiя:

f(x) ≡ а₀ (х тАФ α₁) (х тАФ α₂) .. (х тАФ α_n) (mod p).ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4)

Справдi, тут k = п, отже, степiнь многочлена f_n(x)Ва дорiвнюватиме п-n=0, тобто f_n (х) = а₀.

2.2.1.
Maкcимaльнe число розв'язкiв

Теорема 5. Конгруенцiя п-го степеня за простим модулем не може мати бiльш як п рiзних розв'язкiв.

Справдi, нехай β тАУ який-небудь iнший розв'язок, вiдмiнний вiд α₁, α₂, . . , α_n, тобто

β≠α_i (mod p) (i = 1, 2, тАж , n);

покладаючи тепер в тотожнiй конгруенцii (4) х=β, знайдемо, що

a₀(β тАУ α₁)(β тАУ α₂) тАж (β - α_n) ≡ 0 (mod p),ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (4′)

але рiзницi β тАФ α_i Ваза умовою не дiляться на р, тобто взаiмно простi з р, а в такому разi i iх добуток буде взаiмно простим з р. Звiдси випливаi, що маi мiсце конгруенцiя (4'), тобто f(β) ≡ 0 (mod p), тому а₀ маi дiлитись на р, що суперечить умовi, бо в нас a₀ ≠ 0 (mod p).

Слiд зауважити, по-перше, що ця теорема не пiдтверджуi, взагалi, наявностi розв'язкiв конгруенцii n-го степеня за простим модулем р i, по-друге, для складених модулiв вона зовсiм несправедлива; наприклад, конгруенцiя першого степеня 16 x ≡32 (mod 48), де (16, 48) = 16 i 32 дiлиться на 16, маi шiстнадцять розв'язкiв.

Висновок. Конгруенцiя

f (х)= а₀х^п + а₁х^п-1 + . . . + а_n-1x + a_n ≡ 0 (mod p)

маi бiльш як п- розв'язкiв тодi i тiльки тодi, коли вона тотожна, тобто коли всi ii коефiцiiнти дiляться на р.

Справдi, якщо коефiцiiнти даноi конгруенцii дiляться на р, то вона задовольняiться будь-яким значенням х, тобто вона, тотожна, i число ii розв'язкiв (яке дорiвнюi р) буде бiльш як п (бо ми скрiзь передбачаiмо степiнь конгруенцii не бiльший за р тАФ 1).

Якщо а₀ не дiлиться на р, то це конгруенцiя п-го степеня i за теоремою 5 вона маi не бiльш як п розв'язкiв. Якщо ж а₀ дiлиться на р, але a₁ не дiлиться на р, то степiнь цiii конгруенцii дорiвнюватиме n тАФ 1 i вона за тiiю самою теоремою маi не бiльше п тАФ 1, а тому й не бiльш як п, розв'язкiв. Так можна продовжувати далi, i якщо тiльки не всi коефiцiiнти даноi конгруенцii дiляться на р, то число ii розв'язкiв, очевидно, не може перевищувати п.

2.3. Системи конгруенцiй

Обмежимося системоюВа конгруенцiй:

a₁x ≡b₁Ва (mod m₁); (a₁, m₁) = 1,

a₂x ≡b₂Ва (mod m₂); (a₂, m₂) = 1,

тАжтАжтАжтАжтАжтАжтАжтАжтАжтАжВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (1)

a_kx ≡b_kВа (mod m_k); (a_k, m_k) = 1,

з одним невiдомим, але рiзними модулями.

Розв'язати яку-небудь систему конгруенцiй з одним невiдомимтАФ це означаi знайти такi цiлi значення невiдомого х, якi задовольняли б усi конгруенцii даноi системи. Якщо х ≡ α за деяким модулем i розв'язком системи (1), то весь цей клас чисел прийматимемо за один розв'язок. Якщо дана система маi хоч би один розв'язок, то вона називаiться сумiсною.

Насамперед, зауважимо, що розв'язуючи окремо кожну з конгруенцiй (1), врештi матимемо систему, еквiвалентну данiй:

x ≡ c₁ (mod m₁),

x ≡ c₂ (mod m₂),

тАжтАжтАжтАжтАж.ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)

x ≡ c_k (mod m_k).

Отже, доситьВа умiтиВаВа розв'язуватиВаВа системуВаВа конгруенцiйВаВа (2).

Неважко показати, що коли система (2) сумiсна, то вона маi iдиний розв'язок за модулем М, що дорiвнюi найменшому спiльному кратному чисел m₁, m₂,тАж ,m_k.

2.4. Зведення конгруенцiй за складеним модулем до системи конгруенцiй за простими модулями

Теорема 1.Ва Якщо m₁, m₂, тАж , т_k тАФ попарно взаiмно простi числа, то конгруенцiя

f (х)= а₀х^п + а₁х^п-1 + . . . + а_n-1x + a_n ≡ 0 (mod m₁ m₂ . . . m_k) (1) еквiвалентна системi конгруенцiй:

f(x) ≡ 0 (mod m₁),

f(x) ≡ 0 (mod m₂),ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (2)

тАжтАжтАжтАжтАжтАж.

f(x) ≡ 0 (mod m_k).

При цьому, позначаючи через

S₁, S₂ ,Ва . . . , S_k

числа розв'язкiв окремих конгруенцiйВа (2)Ва за вiдповiдними модулями i через S тАФ число розв'язкiв конгруенцii (1), матимемо:

S = S₁S₂ . . . S_k .

Перша частина твердження безпосередньо випливаi з властивостей 8 i 7, п.1.1. Справдi, припустимо α тАФ розв'язок конгруенцii (1), тобто

f(α) ≡ 0 (mod m₁ m₂ . . . m_k),

а звiдси i поготiв

f(α) ≡ 0 (mod т_i),

тобто α тАФ розв'язок будь-якоi конгруенцii системи (2).

Навпаки, якщо β тАФ розв'язок системи конгруенцiй (2), то матимуть мiсце тотожнi конгруенцii:

f(β) ≡ 0 (mod т_i) (i = 1, 2, тАж , k).

Але тодi (див. властивiсть 7, п.1.1) ця конгруенцiя матиме мiсце i за модулем, який дорiвнюi найменшому спiльному кратному чисел m₁, m₂, тАж , т_k,, тобто, зважаючи на те, що вони попарно взаiмно простi, за модулемВаВа m₁m₂ . . . m_k :

f(β) ≡ 0 (mod m₁ m₂ . . . m_k);

це означаi, що β i також розв'язком конгруенцii (1).

Друге твердження випливаi з таких мiркувань: припустимо, що

х ≡ α_i (mod т_i)

i будь-який розв'язок конгруенцii

f(x) ≡ 0 (mod т_i),

тодi завжди можна знайти iдине число x₁, яке i розв'язком системи лiнiйних конгруенцiй:

х ≡ α₁ (mod т₁),

х ≡ α₂ (mod т₂),

тАжтАжтАжтАжтАжтАжВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа (3)

х ≡ α_k (mod т_k).

Це число x₁ визначаiться за модулем т = m₁m₂ .. m_k; воно буде розв'язком системи (2), а отже, i конгруенцii (1). Але, комбiнуючи кожен розв'язок однiii конгруенцii з системи (2) з кожним розв'язком решти конгруенцiй, ми, очевидно, дiстанемо S₁∙S₂тАжS_k = S лiнiйних систем конгруенцiй типу (3) i, через те що кожна така система маi iдиний розв'язок, який i розв'язком як системи (2), так i конгруенцii (1), то цим i доведено другу частину теореми.

Висновок 1. Якщо хоч одна з конгруенцiй системи (2) не маi розв'язкiв, то й дана конгруенцiя (2) також не матиме розв'язкiв.

Висновок 2. Дослiдження i розв'язування конгруенцii

f(x) ≡ 0 (mod т),

де т = 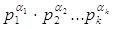ВатАФ канонiчний розклад модуля т тАФ зводиться до дослiдження i розв'язування конгруенцiй:

f(x) ≡ 0 (mod 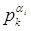)ВаВа (i = 1, 2, .., k).[2]

Це випливаi з того, що числа 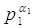, , 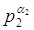.., 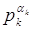Вапопарно взаiмно простi.

Отже, все зводиться до того, що доводиться окремо дослiджувати i розв'язувати конгруенцii виду

f(x) ≡ 0 (mod 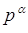),ВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(4)

де p тАФ простеВа число, α тАФ цiле додатне число. Зауважимо, що всякий розв'язок конгруенцii (4) буде розв'язком конгруенцii

f(x) ≡ 0 (mod p).ВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа(5)

Очевидно, якщо конгруенцiя (5) не маi розв'язкiв, то й конгруенцiя (4) розв'язкiв не матиме. Справдi, з припущення виходить, що при жодному цiлому х не маi мiсця конгруенцiя

f(x) ≡ 0 (mod p),

тобто f(х) не дiлиться на р, алеВа тодi f(х) i поготiвВаВа не дiлитиметься на p^α, тобто

f(x) ≠ 0 (mod )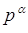

нi при якому цiлому х.

Висновки

Розглянуто конгруенцii, iх означення та основнi властивостi.

Також розглянуто класи чисел за даним модулем та класи розвтАЩязкiв конгруенцii довiльного степеня.

Було звернено увагу на системи конгруенцiй

Доведено цiлий ряд теорем необхiдних при розвтАЩязуваннi конгруенцiй з невiдомою величиною.

РозвтАЩязано декiлька прикладiв;

Пiсля доведення теорем, рiшення прикладiв та введення означень була отримана певна кiлькiсть висновкiв щодо тих чи iнших операцiй над конгруенцiями.

Список литературы

Бородiн О.РЖ., Теорiя чисел. тАЬРадянська школатАЭ, К., 1965. тАУ 244с.

Бухштаб А.А., Теория чисел. Учпедгизд., М., 1960. тАУ 375с.

Окунев Л.Я., Краткий курс теории чисел, Учебное пособие для пединститутов, М., 1956

Сушкевич А.К., Теорiя чисел. Видавництво Харкiвського Державного Унiверситета РЖменi А.М.Горького, Х.,1954.

Приложение

СХЕМА ГОРНЕРА

P_n(x) = a_nxⁿ + a_n-1x^n-1 + тАж + a₁x + a₀ ;

P_n-1(x) = S_n-1(x)(x тАУ c) + R ;

S_n-1(x) = b_n-1x^n-1 + b_n-2x^n-2 + тАж+b₁x + b₀ ;

ВаВаВаВаВа (x тАУ c);

a_n = b_n-1 ;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа b_n-1 = a_n ;ВаВаВаВаВа

a_n-1 = b_n-2 тАУ cb_n-1 ;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа b_n-2 = a_n-1 + cb_n-1 ;

a_n-2 = b_n-3 тАУ cb_n-2 ;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа b_n-3 = a_n-2 + cb_n-2 ;

тАжтАжтАжтАжтАжтАжтАжВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа ВаВаВаВатАжтАжтАжтАжтАжтАжтАж

a₀ = R тАУ cb₀ ;ВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВаВа R = a₀ + cb₀ ;

Таблиця

СТРУКТУРНЕ ПРЕДСТАВЛЕННЯ СХЕМИ ГОРНЕРА

	an	an-1	an-2	тАжтАж.	a0
c	bn-1	bn-2	bn-3	тАжтАж.	R

Вместе с этим смотрят:

"Инкарнация" кватернионов

* Алгебры и их применение

*-Алгебры и их применение

10 способов решения квадратных уравнений

Bilet