Классические основания квантовой механики
Валерий Эткин
Немалое число людей, так или иначе связанных с наукой, испытывает острую неудовлетворенность существующей тенденцией современной физики Влугадывать уравнения, не обращая внимания на физические модели или физическое объяснениеВ» (Р. Фейнман, 1976 г.). В полной мере относится это и к основополагающему уравнению квантовой механики, явившемуся плодом гениальной интуиции его автора (Э. Шрёдингер, 1926 г.). Между тем уравнение такого типа можно получить и из классической физики, если допустить, что при торможении электронов в их движении по устойчивым некруговым (например, эллиптическим) орбитам их кинетическая энергия Ek переходит не только в потенциальную энергию атома как целого, но и частично отдается последним в окружающую среду в форме лучистой энергии*.
* Последнее следует из неравновесной термодинамики (Де Гроот С., Мазур П., 1964; Эткин В.А., 1999), согласно которой протекание какого-либо неравновесного процесса (в том числе процесса торможения электрона) связано с преодолением всех действующих в системе термодинамических сил, т.е. с преобразованием энергии в другие ее формы, соответствующие этим силам. Из нее следует также, что при этом излучают не электроны, а атом как неравновесная в целом система, поскольку энергия принадлежит, строго говоря, всей совокупности взаимодействующих (взаимно движущихся) тел или частей тела, и лишь в исключительных случаях может быть приписана одному из них.
Это возможно, если атом на различных фазах орбитального движения электронов (торможение тАУ ускорение) то излучает, то поглощает одно и то же количество энергии. В противном случае электрон переходит на нижележащую или вышележащую орбиту, параметры которой определяются величиной потерянной или приобретенной энергии. Соответственно изменяется и частота излучения. В этом порядке идей переход на нижележащую орбиту является следствием излучения, а не наоборот (как в теории Бора). Такой процесс излучения или поглощения имеет конечную длительность, определяемую орбитальной скоростью электрона и длиной участков торможения или ускорения. Потому-то излучение и осуществляется порциями (квантами).
Поскольку излучение происходит на тех участках орбиты, где происходит торможение электрона в его движении относительно ядра, частота излучения ν равна, очевидно, числу оборотов электрона в единицу времени. Последнее представляет собой частное от деления модуля орбитальной скорости v на длину орбиты (или эквивалентной ей окружности радиусом a (ν = v/2πa). В таком случае соответствующая этой частоте длина волны излучения λ ≡ c/ν определяется простым выражением:
λ = 2πca/ν = 2πmeca/meν = h/pe , | (1) |
где с тАУ скорость света в вакууме; me тАУ масса покоя электрона; pe = meν тАУ его импульс; h = 2πmeca тАУ постоянная для данной орбиты величина.
Согласно этому выражению, каждому виду атомов с некруговыми орбитами электронов соответствуют определенные длины волн излучения, зависящие от свойств вещества(импульса электронов и радиуса их орбит). Тем самым гипотеза де Бройля (1926 г.) о том, что волновые свойства присущи всем веществам, получает обоснование в рамках классической физики. Легко видеть, что при этом частота излучения ν согласно (1) оказывается пропорциональной импульсу электрона pe:
Это положение также соответствует идеям де Бройля.
Таким образом, при движении электронов по устойчивым некруговым орбитам в атомах возникает колебательный процесс, обусловленный циклическим изменением кинетической энергии электронов Ek. Этот процесс описывается известным уравнением монохроматической пространственной волны

| (3) |
где ψ тАУ Влволновая функцияВ», т.е. параметр системы, являющийся функцией пространственных координат и отклоняющийся в колебательном процессе от своего равновесного значения.
Учитывая, что в соответствии с соотношением (1) λ2 = h2/p2 и p2 = 2m0Ek, где Ek определяется разностью между полной энергией атома (его гамильтонианом) Е и потенциальной энергией U, после подстановки в (3) и простейших преобразований приходим к основополагающему уравнению квантовой механики в виде:
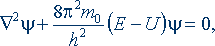
| (4) |
Это уравнение отличается от стационарного (не зависящего от времени) уравнения Шрёдингера тем, что в нем универсальная постоянная Планка ħ заменена функцией радиуса орбиты h = h(a). Связь между ħ и h нетрудно установить, если в соответствии с ОТО выразить ν через импульс фотона pф известным соотношением ħν = pфc. Тогда из (1) следует, что h = ħpe/pф. Так Влперекидывается мостикВ» между квантовой и классической механикой.
Предложенный вывод ВлклассическогоВ» аналога уравнения Шрёдингера не опирается на какие-либо гипотезы и постулаты. Это выгодно отличает его от обоснования, данного самим Шрёдингером, которое всегда представлялось исследователям не вполне убедительным. В особенности это замечание касается физического смысла функции ψ. В его толковании среди наиболее крупных физиков-теоретиков до сих пор отсутствует единодушие. В большинстве своем они трактуют функцию ψ как величину, квадрат которой, будучи умноженным на элемент объема dV, характеризует вероятность ψ2dV нахождения частицы в заданной области пространства. Это понятие предполагает индетерминизм даже на уровне элементарных процессов, т.е. утрату квантовой механикой способности предсказывать события (определять последующие значения параметров по предшествующим). Вместе с тем применение понятия вероятности к отдельному атому или отдельной молекуле в известный момент времени довольно бессмысленно, так как последние обладают вполне определенным значением кинетической энергии, находятся в определенном месте и движутся в определенном направлении. В изложенном же порядке идей волновая функция приобретает простой и ясный смысл энергии электрона как функции параметров его орбитального движения. Так решается, пожалуй, самый принципиальный из физических вопросов, связанных с квантовой механикой. Наряду с этим устраняется одна из принципиальных трудностей классической электродинамики, состоящая в невозможности объяснить существование устойчивых орбит электронов из-за кажущейся неизбежности их ВлпаденияВ» на ядро при излучении ими энергии. Такое излучение с позиций классической электродинамики должно иметь место даже тогда, когда величина скорости электрона остается неизменной (изменяется лишь направление вектора скорости на орбите). Если же излучение порождается исключительно процессом превращения кинетической энергии в другие формы, направление скорости уже не играет роли.
Известно, что консервативные системы (E = const), подчиняющиеся этому уравнению, могут обладать только вполне определенными значениями энергии. Это же следует и из выражения (1), согласно которому определенным длинам волн спектра излучения атомов соответствуют определенные радиусы электронных орбит. Таким образом, идея ВлквантованияВ» энергии электронов и их орбит также естественным образом вытекает из классических представлений.
Предложенный подход выгодно отличается также от атомной механики Бора, которая хотя и придерживалась в основном классических принципов, потребовала ряда дополнительных постулатов. Наиболее уязвимым из них явилось допущение о том, что электрон излучает в момент перехода с одной орбиты на более низкую, так что частота излучаемых волн зависит как от начальной, так и от конечной энергии атома. Отсюда следовало, что электрон либо каким-то непостижимым образом ВлзнаетВ» о будущей орбите, либо излучает только после попадания на конечную стационарную орбиту. Ввиду неприемлемости обоих следствий это положение всегда оставалось самым непонятным и слабым звеном в теории Бора. С изложенных позиций электрон переходит на нижележащую орбиту лишь после того, как атом излучает энергию. Тем самым устраняется основная трудность теории Бора.
Представление о том, что излучают не электроны, а атомы, объясняет также результаты опытов по Влдифракции электроновВ», поскольку позволяет допустить, что дифракционную картину создают не электроны, а возбуждаемые ими атомы вокруг отверстия, через которое они пролетают. Тем самым проливается новый свет на дуализм Влволна тАУ частицаВ».
Однако наиболее важным результатом предложенного подхода являются дополнительные возможности нахождения параметров электронных орбит по данным спектроскопических наблюдений. В частности, по известным длинам волн излучения λ или волновым числам νλ ≡ 1/λ = ν/c можно найти радиус i-й устойчивой электронной орбиты ai атомов, излучающих на этой частоте. Исходя из равенства на такой орбите центробежной силы fω = mev2/ai силе взаимодействия электрона с ядром fr = e2/ai2, после подстановки в выражение νλ = p/hc несложно найти радиус электронной орбиты, соответствующий определенной частоте излучения:
ai = (e2/4π2c2meνλ2)тАУ3 м. | (5) |
После этого нетрудно найти среднюю орбитальную скорость электронов v = 2πaiν, кинетическую энергию электрона на i-й орбите Ek = mev2/2 и число оборотов электрона на орбите n = ν. Однако вопрос о соответствии такого подхода результатам экспериментов остается при этом открытым.
Де Бройль Л. Ann. De Phys, V. 10, 1925, p. 22. Перевод с фр.: ВлВведение в волновую механикуВ». тАУ Харьков тАУ Киев, 1934.
Фейнман Р. Нобелевская лекция. Пер. с англ. М.: Наука, 1976.
Шрёдингер Э. Ann. Phys., Bd. 79, 1926, p. 361, 489; Bd. 80, 1926, p. 437; Bd. 81, 1926, p. 109. Перевод с нем.: ВлЧетыре лекции по волновой механикеВ». тАУ Харьков тАУ Киев, 1936.
Де Гроот С., Мазур П. Неравновесная термодинамика, М.: Мир, 1964.
Эткин В.А. Термодинамика неравновесных процессов переноса и преобразования энергии. Саратов: Изд-во СГУ, 1991.
Вместе с этим смотрят:
"Инкарнация" кватернионов
* Алгебры и их применение
*-Алгебры и их применение
10 способов решения квадратных уравнений
Bilet