Опыты Араго и теория Френеля

Современная наука не отрицает истинности Френелевской формулы частичного увлечения эфира движущимися телами (средами) тАУ Вл..и сейчас одного из наиболее важных явлений в движущихся телахВ» [1]. В современной теории относительности формула Френеля рассматривается как частный случай более общей ВлрелятивистскойВ» формулы сложения скоростей.

Любая научная теория может считаться истинной, если она удовлетворяет, по крайней мере, следующим критериям:

основана на предположениях, соответствующих реальной физической действительности;

является внутренне логически непротиворечивой;

предсказываемые теорией явления наблюдаются в реальной физической действительности.

Как полагают, формула Френеля основана на вполне достоверных данных опытов Араго и подтверждается опытами Физо. Однако исследование как опытов Араго, так и других известных опытов и явлений, не дают оснований считать общепринятое мнение соответствующим действительности.

Опыт Араго

В 1801г. Араго выполнил опыт, цель которого заключалась в проверке выдвинутого Мичелом предположения, что движение призмы или линзы должно сопровождаться изменением ее коэффициента преломления. Мичел считал, что при полностью неувлекаемом веществом линзы эфире скорость света внутри линзы будет равна c/n+v при движении линзы в одном направлении и c/n тАУ v при движении линзы в противоположном направлении. В своих опытах Араго использовал свет от одной из звезд. Он не обнаружил никакого эффекта, обусловленного движением линзы вместе с Землей относительно звезды, и пришел к выводу, что движение линзы вместе с Землей Вл..на показатель преломления не влияет. Это заключение правильно, действительно не влияетВ», соглашается с ним Л.И.Мандельштам в [1]. В действительности, это не так. Известно, что движение приемника света, в данном случае тАУ линзы, относительно источника света сопровождается, как это установил Доплер, изменением частоты света, принимаемого приемником. Коэффициент преломления линзы, в свою очередь, зависит от частоты света: Вл..факт зависимости показателя преломления от частоты света называется дисперсией, так как именно из-за дисперсии свет раскладывается призмой в спектрВ» [2].

Таким образом, коэффициент преломления линзы зависит от состояния ее движения относительно источника света. Опыты Араго оказались недостаточно точными. Однако во времена Араго эффект Доплера еще не был известен, вследствие чего Араго счел результаты своих опытов вполне достоверными. Результаты опытов Араго можно было объяснить полным увлечением эфира веществом линзы, однако как объяснить само полное увлечение Араго не знал и обратился за разъяснениями к Френелю. Френель, не подвергая результаты опытов Араго ни малейшему сомнению, предложил гипотезу, согласно которой эфир увлекается движущимися телами не полностью, а частично, вследствие чего скорость Влэфирного ветраВ» внутри движущегося тела (или среды) оказывается равной:

v = v(1 тАУ 1/n²),

где v тАУ скорость движения тела (среды) относительно внешнего по отношению к этому телу (среде) эфиру; n тАУ коэффициент преломления вещества движущегося тела или среды.

Каким же образом гипотеза Френеля объясняет результаты опытов Араго? Пусть n²=2. Тогда частичное, по Френелю, увлечение эфира внутри движущейся линзы может уменьшить в 2 раза эффект, обусловленный ее движением, тогда как требуется полностью его исключить. Очевидно, суть дела заключается не в частичном увлечении эфира движущейся линзой, а в том, что линза в опыте Араго находится внутри атмосферы Земли, коэффициент преломления которой можно считать равным 1. Тогда частичное, по Френелю, увлечение эфира применительно к атмосфере означает полное его увлечение, так как при n=1 скорость Влэфирного ветраВ» в атмосфере Земли оказывается равной нулю тАУ Влэфирный ветерВ», обусловленный движением Земли, в атмосфере Земли не возникает, а потому не может возникнуть и в линзе, погруженной в атмосферу.

Гипотеза Френеля встретила многочисленные возражения. Нам же достаточно ограничиться тем обстоятельством, что гипотеза Френеля основана на ошибочных результатах опытов Араго, а потому не может быть правильной. Естественно, поэтому, что любая другая правильная теория не должна объяснять частичное увлечение эфира, так как такого явления в реальной действительности не существует. Более того, теория, объясняющая частичное увлечение эфира является ошибочной по той же причине тАУ она объясняет несуществующее в природе явление.

Общепринятым является мнение, что Френелевский коэффициент увлечения подтверждается в опытах Эйхенвальда с возвратно-поступательным движением диэлектрика. В действительности имеет место взаимодействие части зарядов на пластинах с зарядами на диэлектрике, так как площадь поверхности диэлектрика в данном опыте меньше площади поверхности каждой из пластин, между которыми движется диэлектрик. Точно так же, и в опытах Вильсона различная величина заряда, возникающего на внешней и внутренней поверхности цилиндра, обусловлена тем, что и площадь, и линейная скорость вращения внешней поверхности цилиндра больше площади и линейной скорости вращения внутренней поверхности того же цилиндра. Таким образом, по крайней мере, в электродинамике Френелевский коэффициент увлечения не подтверждается никакими опытами.

Опыты Физо

Как утверждает Л.И.Мандельштам в [1], ВлВ 1851г. Физо подтвердил Френелевскую формулу коэффициента увлечения опытами с распространением света в движущейся воде..В». Схема опыта Физо изображена на рис.1.

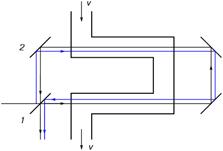
Рис. 1. Схема опыта Физо

Жидкость течет в изогнутой трубке со скоростью v. Луч света от источника попадает на полупрозрачное зеркало 1 и расщепляется на два луча: один луч отклоняется вправо и, попадая в трубку с жидкостью, движется против ее течения, отражается от системы зеркал и, выйдя из трубки и пройдя через полупрозрачное зеркало, попадает на экран.

Второй луч (изображен сплошной линией) отражается от зеркала 2 и движется в том же направлении, что и жидкость в трубке. Отражаясь затем от системы зеркал, этот луч света также попадает на экран. В результате на экране возникает интерференционная картина из чередующихся светлых и темных полос. Измерив их ширину, можно определить скорость движения лучей света в движущейся жидкости, тем самым тАУ и степень увлечения эфира движущейся жидкостью. Ширина интерференционных полос зависит от разности времен хода каждого из лучей света в движущейся жидкости. Согласно Физо, время движения одного из лучей света равно:

T₁ = L/(c/n + kv),

время движения другого луча равно:

T₂ = L/(c/n тАУ kv),

где L тАУ путь, который проходит луч света в движущейся жидкости; n тАУ коэффициент преломления жидкости; k тАУ Френелевский коэффициент увлечения эфира движущейся жидкостью; v тАУ скорость движения жидкости в трубке.

Тогда разность времен хода лучей будет равна:

T₂ тАУ T₁ = L/(c/n тАУ kv) тАУ L/(c/n + kv) = 2Lkvn²/c²(1 тАУ k²v²n²/c²).

Пренебрегая величиной k²v²n²/c² вследствие ее малости, получим:

T₂ ^тАУ T₁ = 2Lkvn²/c².

Физо полагал, что в данном случае k = 1 тАУ 1/n². Так как для воды n=1,33, численное значение k оказывается равным 0,44. Физо получил из опыта величину k=0,46, как будто подтвердив тем самым гипотезу Френеля. В действительности, это не так.

Предположим, что некоторый наблюдатель, находящийся внутри жидкости, движется вместе с жидкостью в трубке и с той же скоростью v. При полностью неувлекаемом эфире скорость эфира внутри жидкости относительно этого наблюдателя будет, очевидно, равна v; при полностью увлекаемом движущейся жидкостью эфире скорость эфира относительно того же наблюдателя будет равна нулю. Вследствие частичного, по Френелю, увлечения, часть эфира увлекается движением жидкости и движется в том же направлении, что и жидкость. Скорость этой увлекаемой части равна v/n². Следовательно, скорость движения эфира внутри жидкости относительно наблюдателя, также находящегося внутри жидкости и движущегося с той же скоростью, что и жидкость, будет равна v_э=vтАУv/n²=v(1тАУ1/n²).

С точки зрения неподвижного наблюдателя, находящегося вне движущейся жидкости, при полностью неувлекаемом эфире скорость эфира равна нулю и внутри движущейся жидкости, и вне ее. При полностью увлекаемом эфире скорость его движения в трубке относительно внешнего наблюдателя будет равна v. При частичном увлечении эфира скорость его движения в направлении движения жидкости равна v/n². Следовательно, относительно внешнего неподвижного наблюдателя эфир в трубке движется со скоростью v/n². Коэффициент увлечения эфира с точки зрения неподвижного наблюдателя равен 1/n².

В опыте Физо наблюдатель тАУ экран, на котором появляются интерференционные полосы тАУ находится вне жидкости, движущейся в трубке. Следовательно, скорость движения эфира в трубке, обусловленная движением жидкости, относительно этого экрана равна v/n². Тогда коэффициент увлечения эфира равен 1/n², а не 1тАУ1/n², как полагал Физо. При n=1,33 получим k=0,56, тогда как Физо получил k=0,46. Учитывая ошибку, допущенную Физо при постановке его опыта, результаты этого опыта следует признать недостоверными.

Продолжением описанного выше опыта Физо явился его опыт 1859г. Установив, как он полагал, Вл..справедливость теории частичного увлечения для жидких и газообразных сред, Физо решил проверить ее для твердых тел. Для этой цели он использовал явление поворота плоскости поляризации при преломлении поляризованного света на границе двух сред. Угол поворота зависит от показателя преломления среды, а последний тАУ от скорости света в данной среде. По мнению Физо, изменение ориентации прибора относительно направления поступательного движения Земли должно было изменить относительную скорость света в среде. Проанализировав результаты 2000 опытов, Физо в 1859г. объявил о подтверждении формулы Френеля и о наличии влияния движения Земли на поворот плоскости поляризации.В» [3]. Сама постановка этого опыта свидетельствует о непонимании Физо сути теории Френеля, согласно которой Влэфирный ветерВ», обусловленный движением Земли, в атмосфере Земли не возникает, а потому не может быть обнаружен никакими опытами. ВлНикто не мог обнаружить ошибку в этих опытах, а трудность их постановки была столь велика, что только через 43 года они были повторены и дали отрицательный результатВ» (У.И.Франкфурт). Однако главная ошибка Физо, свидетельствующая о непонимании им сути теории Френеля, так и осталась незамеченной.

Вл..в 1868г. Хук поставил опыт, в котором наблюдал земной источник света в телескоп через двухметровый столб воды. Отсутствие предполагаемого сдвига изображения, обусловленного суточным вращением Земли, Хук объяснил на основе теории Френеля. Он пришел к выводу, что Френелевский коэффициент увлечения справедлив с точностью до 2%.. В свою очередь Клинкерфус поставил аналогичный опыт с 8-дюймовым столбом воды и получил увеличение постоянной аберрации на 7,1" (по его теории ожидалось увеличение на 8"). Для разрешения этого противоречия серию точных опытов провел в 1871..1872гг. Эйри. Он наблюдал звезду вблизи зенита с помощью вертикально установленного телескопа высотой 35,3 дюйма, заполненного водой. По теории Клинкерфуса за полгода угловое смещение звезды должно было составить около 30", в то время как на опыте смещение не превышало 1" и лежало в пределах ошибок экспериментаВ». (У.И.Франкфурт).

Постановка этих опытов, как и опытов Физо 1859г., свидетельствует о непонимании исследователями сути теории Френеля тАУ вследствие полного увлечения эфира атмосферой Земли Влэфирный ветерВ», обусловленный движением Земли, в атмосфере Земли не возникает, а поэтому не может возникнуть и в телескопе, заполненном водой. Исходя из этого, опыты Эйри являются наиболее достоверными.

Непонимание сути теории Френеля сохранилось в науке вплоть до настоящего времени. Как считает У.И.Франкфурт, в теории Френеля ВлВсе происходит так, как будто эфир внутри (здесь и далее выделено мной тАУ В.П.) тела движется относительно внешнего эфира со скоростью v(1тАУ1/n²), т.е. медленнее, чем само тело. Частичное увлечение эфира Френель понимал в том смысле, что движущееся тело увлекает не весь содержащийся в нем эфир, а только ту часть, которая соответствует превышению плотности эфира в теле над его плотностью в окружающей среде. В теории Френеля можно выделить следующие основные положения:

1) внешний эфир совершенно не увлекается неподвижными телами;

2) внутренний эфир почти не увлекается непрозрачными телами;

3) внутренний эфир частично увлекается прозрачными телами.

Установив справедливость теории частичного увлечения для жидких и газообразных сред, Физо решил проверить ее для твердых телВ».

Очевидно, что Физо считал, что газообразные среды увлекают эфир внутри них в соответствии с формулой Френеля, как и жидкие среды или твердые тела. Это мнение считается правильным или, по крайней мере, не отвергается современной наукой. Однако как только речь идет о возможности обнаружения абсолютного движения Земли (т.е. движения Земли относительно эфира) возможность увлечения эфира атмосферой Земли полностью исключается:

ВлНаиболее простой представлялась гипотеза полного увлечения: тела увлекают за собой эфир подобно тому, как Земля увлекает все находящиеся на ней тела и атмосферуВ» (У.И.Франкфурт).

Очевидно, что тела, находящиеся на Земле, как и атмосфера, являются внешними по отношению к поверхности Земли, находятся Влна нейВ», следовательно, увлечение эфира Землей рассматривается как увлечение внешнего по отношению к Земле эфира, а не как увлечение эфира внутри атмосферы Земли. ВлВ этом случае (т.е. в случае увлечения эфира поверхностью Земли тАУ В.П.) все оптические явления при движении тел происходят точно так же, как и в покое, и опыт Араго легко объясним. Однако аберрацию звезд объяснить нельзя. Это обстоятельство послужило причиной того, что Юнг отверг гипотезу полного увлечения (Землей внешнего по отношению к ней эфира тАУ В.П.) и допустил, что движущаяся Земля не влияет на состояние эфира, который проходит через нее так же легко, как ветер сквозь рощу. Тогда аберрация объяснима. Объяснить одновременно опыт Араго и аберрацию на основе рассмотренных гипотез полностью увлекающегося (поверхностью Земли тАУ В.П.) или неподвижного (т.е. не увлекающегося поверхностью Земли тАУ В.П.) эфира не представлялось возможнымВ». (У.И.Франкфурт). Однако если учесть увлечение эфира атмосферой Земли (внутри атмосферы Земли), тогда можно объяснить одновременно и опыт Араго, и аберрацию звезд.

ВлПервую математическую теорию аберрации на основе полного увлечения эфира дал Стокс. Скорость эфира вблизи поверхности Земли принималась равной скорости Земли. По мере удаления от Земли она убывает до нуляВ» (У.И.Франкфурт). Здесь очевидно имеется в виду увлечение внешнего по отношению к Земле эфира, тогда как в теории Френеля речь идет об увлечении эфира внутри движущихся тел или сред. Атмосфера Земли, как считал Стокс, не влияет на характер увлечения эфира. Однако если атмосфера Земли как среда увлекает эфир в соответствии с формулой Френеля, т.е. внутри атмосферы Земли, и опыты Физо, как считается, подтверждают увлечение эфира внутри движущихся сред, то картина увлечения эфира прямо противоположна теории Стокса: так как коэффициент преломления воздуха уменьшается с увеличением расстояния от поверхности Земли, скорость Влэфирного ветраВ» в атмосфере Земли уменьшается от величины около 18м/с у поверхности Земли при n=1,0003 до нуля при n=1, т.е. Влэфирный ветерВ», обусловленный движением Земли, в верхних слоях атмосферы Земли отсутствует, следовательно, не может возникнуть и у поверхности Земли. В этом и заключается, на наш взгляд, главная ошибка, допущенная наукой при объяснении результатов опыта Майкельсона тАУ Морли.

Заключение

1. Теория Френеля основана на ошибочных результатах опытов Араго, не подтверждается в опытах Эйхенвальда и Вильсона; опыты Физо также не являются достаточно убедительным доказательством истинности Френелевской формулы сложения скоростей. Таким образом, теория Френеля не удовлетворяет двум критериям истинности, а потому не может считаться истинной. По этой причине не может считаться истинной любая теория, включающая или обосновывающая Френелевскую формулу сложения скоростей.

2. Так как результаты опытов Араго являются ошибочными, согласовывать результаты этих опытов с явлением аберрации нет необходимости.

3. Согласовать опыты Майкельсона тАУ Морли и явление аберрации можно только при условии полного увлечения эфира внутри атмосферы Земли при ненулевой ее вязкости и полного неувлечения эфира атмосферой при нулевой ее вязкости.

4. Опыты Физо, а впоследствии и опыты Гарреса подтверждают, что эфир внутри движущихся сред тАУ жидкости в опыте Физо, прозрачных твердых кристаллов в опыте Гарреса тАУ увлекается движением этих сред, т.е. движется с определенной скоростью относительно неподвижного экрана, на котором наблюдается изменение интерференционной картины, соответствующей скорости движения эфира. Таким образом, и в оптике, и в электродинамике, как это подтверждают опыты Эйхенвальда с вращающимся диэлектриком, движение эфира относительно наблюдателя всегда сопровождается вполне наблюдаемыми эффектами даже при скорости движения порядка нескольких метров в минуту. Предположение Эйнштейна, поддерживаемое официальной наукой, что с понятием ВлэфирВ» нельзя связывать понятие ВлдвижениеВ», не соответствует действительности.

5. В опытах Физо скорость движения эфира относительно экрана или, что то же самое, скорость движения экрана относительно эфира внутри движущейся жидкости составляла величину порядка нескольких метров в минуту, при этом изменение интерференционной картины оказывалось вполне наблюдаемым, хотя точность измерения этого изменения оказалась недостаточно высокой.

В опытах Майкельсона тАУ Морли ожидаемая скорость движения прибора относительно эфира составляла величину порядка 30 километров в секунду, при этом никакого изменения интерференционной картины обнаружить не удалось. Так как, согласно опытам Физо, движение относительно эфира всегда сопровождается изменением интерференционной картины, необходимо заключить, что в опытах Майкельсона тАУ Морли отсутствовало движение прибора относительно эфира, что вполне соответствует предположению о полном увлечении эфира внутри атмосферы Земли.

Л.И.Мандельштам. Лекции по оптике, теории относительности и квантовой механике. тАУ М.Наука, 1971.

Р.Фейнман, Р.Лейтон, М.Сэндс. Фейнмановские лекции по физике. тАУ М., ВлМирВ», 1976.

У.И.Франкфурт. Оптика движущихся сред и специальная теория относительности. Эйнштейновский сборник 1977. тАУ М., Наука, 1980.

Вместе с этим смотрят:

"Инкарнация" кватернионов

* Алгебры и их применение

*-Алгебры и их применение

10 способов решения квадратных уравнений

Bilet